20.6: Area of solid parallelograms
- Page ID
- 23715
Let \(\square ABCD\) be a parallelogram in the Euclidean plane, \(a=AB\) and \(h\) be the distance between the lines \((AB)\) and \((CD)\). Then
\(\text{area }(\blacksquare ABCD)=a\cdot h.\)
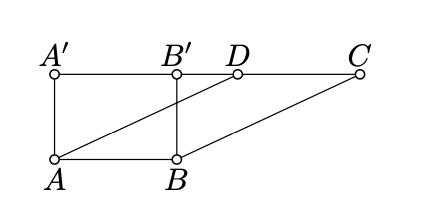
- Proof
-
Let \(A'\) and \(B'\) denote the foot points of \(A\) and \(B\) on the line \((CD)\).
Note that \(ABB'A'\) is a rectangle with sides \(a\) and \(h\). By Theorem 20.5.1,
\[\text{area }(\blacksquare ABB'A')=h\cdot a.\]
Without loss of generality, we may assume that \(\blacksquare ABCA'\) contains \(\blacksquare ABCD\) and \(\blacksquare ABB'A'\). In this case \(\blacksquare ABCA'\) admits two subdivisions:
\(\blacksquare ABCA'=\blacksquare ABCD\cup\blacktriangle AA'D=\blacksquare ABB'A'\cup\blacksquare BB'C.\)
\[\begin{aligned} \text{area }( \blacksquare ABCD)&+\text{area }(\blacktriangle AA'D)= \\ &= \text{area }(\blacksquare ABB'A')+ \text{area } (\blacktriangle BB'C). \end{aligned}\]
Note that
Indeed, since the quadrangles \(ABB'A'\) and \(ABCD\) are parallelograms, by Lemma 7.5.1, we have that \(AA'=BB'\), \(AD=BC\), and \(DC=AB=A'B'\). It follows that \(A'D=B'C\). Applying the SSS congruence condition, we get 20.6.3.
In particular,
\[\text{area }(\blacktriangle BB'C)=\text{area } (\blacktriangle AA'D). \]
Subtracting 20.6.4 from 20.4.2, we get that
\[\text{area } (\blacksquare ABCD)=\text{area }(\blacksquare ABB'D).\]
It remains to apply 20.6.1.
Assume \(\square ABCD\) and \(\square AB'C'D'\) are two parallelograms such that \(B'\in[BC]\) and \(D\in [C'D']\). Show that
\(\text{area }(\blacksquare ABCD)=\text{area }(\blacksquare AB'C'D').\)
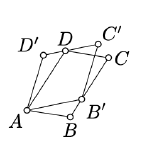
- Hint
-
Suppose that \(E\) denotes the point of intersection of the lines \((BC)\) and \((C'D')\).
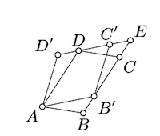
Use Proposition \(\PageIndex{1}\) to prove the following two identities:
\(\begin{array} {l} {\text{area } (\blacksquare AB'ED) = \text{area } (\blacksquare ABCD),} \\ {\text{area } (\blacksquare AB'ED) = \text{area } (\blacksquare AB'C'D')} \end{array}\)


