20.8: Area method
- Page ID
- 58355
In this section we will give examples of slim proofs using the properties of area. Note that these proofs are not truly elementary since the price one pays to introduce the area function is high.
We start with the proof of the Pythagorean theorem. In the Elements of Euclid, the Pythagorean theorem was formulated as equality 20.8.1 below and the proof used a similar technique.
Proof. We need to show that if \(a\) and \(b\) are legs and \(c\) is the hypotenuse of a right triangle, then
\(a^2+b^2=c^2.\)
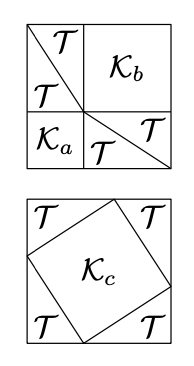
Suppose that \(\mathcal{T}\) denotes the right solid triangle with legs \(a\) and \(b\) and \(\mathcal{K}_{x}\) the solid square with side \(x\).
Let us construct two subdivisions of \(\mathcal{K}_{a+b}\):
- Subdivide \(\mathcal{K}_{a+b}\) into two solid squares congruent to \(\mathcal{K}_a\) and \(\mathcal{K}_b\) and 4 solid triangles congruent to \(\mathcal{T}\), see the first diagram.
- Subdivide \(\mathcal{K}_{a+b}\) into one solid square congruent to \(\mathcal{K}_c\) and 4 solid right triangles congruent to \(\mathcal{T}\), see the second diagram.
Applying Proposition 20.4.2 few times, we get that
\(\begin{aligned} \text{area }\mathcal{K}_{a+b} &= \text{area }\mathcal{K}_{a}+\text{area } \mathcal{K}_{b} +4\cdot\text{area }\mathcal{T}= \\ &=\text{area }\mathcal{K}_{c}+4\cdot\text{area }\mathcal{T}.\end{aligned}\)
Therefore,
\[\text{area }\mathcal{K}_{a}+\text{area }\mathcal{K}_{b}=\text{area }\mathcal{K}_{c}.\]
By Theorem 20.5.1,
\(\text{area }\mathcal{K}_x=x^2,\)
for any \(x>0\). Hence the statement follows.
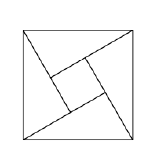
Build another proof of the Pythagorean theorem based on the diagram.
(In the notations above it shows a subdivision of \(\mathcal{K}_c\) into \(\mathcal{K}_{a-b}\) and four copies of \(\mathcal{T}\) if \(a>b\).)
- Hint
-
Assuming \(a > b\), we subdivided \(\mathcal{Q}_c\) into \(\mathcal{Q}_{a - b}\) and four triangles congruent to \(\mathcal{T}\). Therefore
\[\text{area } \mathcal{Q}_c = \text{area } \mathcal{Q}_{a - b} + 4 \cdot \text{area } \mathcal{T}.\]
According to Theorem 20.7.1, \(\text{area } \mathcal{T} = \tfrac{1}{2} \cdot a \cdot b\). Therefore, the identity 20.8.2 can be written as
\(c^2 = (a - b)^2 + 2 \cdot a \cdot b.\)
Simplifying, we get the Pythagorean theorem.
The case \(a = b\) is yet simpler. The case \(b > a\) can be done the same way.
Show that the sum of distances from a point to the sides of an equilateral triangle is the same for all points inside the triangle.
- Hint
-
If \(X\) is a point inside of \(\triangle ABC\), then \(\blacktriangle ABC\) is subdivided into \(\blacktriangle ABX\), \(\blacktriangle BCX\), and \(\blacktriangle CAX\). Therefore
\(\text{area } (\blacktriangle ABX) + \text{area } (\blacktriangle BCX) + \text{area } (\blacktriangle CAX) = \text{area } (\blacktriangle ABC).\)
Set \(a = AB = BC = CA\). Let \(h_1, h_2\), and \(h_3\) denote the distances from \(X\) to the sides \([AB]\), \([BC]\), and \([CA]\). Then by Theorem 20.7.1,
\(\text{area } (\blacktriangle ABX) = \dfrac{1}{2} \cdot h_1 \cdot a\), \(\text{area } (\blacktriangle BCX) = \dfrac{1}{2} \cdot h_2 \cdot a\), \(\text{area } (\blacktriangle CAX) = \dfrac{1}{2} \cdot h_3 \cdot a\).
Therefore,
\(h_1 + h_2 + h_3 = \dfrac{2}{a} \cdot \text{area } (\blacktriangle ABC).\)
Assume that two triangles \(ABC\) and \(A'B'C'\) in the Euclidean plane have equal altitudes dropped from \(A\) and \(A'\) respectively. Then
\[\dfrac{\text{area }(\blacktriangle A'B'C')}{\text{area }(\blacktriangle ABC)} = \dfrac{B'C'}{BC}.\]
In particular, the same identity holds if \(A=A'\) and the bases \([BC]\) and \([B'C']\) lie on one line.
- Proof
-
Let \(h\) be the altitude. By Theorem 20.7.1,
\(\dfrac{\text{area }(\blacktriangle A'B'C')}{\text{area }(\blacktriangle ABC)} = \dfrac{\frac12 \cdot h\cdot B'C'}{\frac12 \cdot h\cdot BC} = \dfrac{B'C'}{BC}.\)
Now let us show how to use this claim to prove Lemma 8.4.1. First, let us recall its statement:
If \(\triangle ABC\) is nondegenerate and its angle bisector at \(A\) intersects \([BC]\) and the point \(D\). Then
\(\dfrac{AB}{AC} =\dfrac{DB}{DC}.\)
- Proof
-
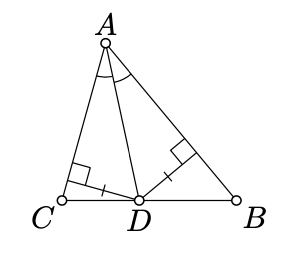
Applying Claim \(\PageIndex{1}\), we get that
\(\dfrac{\text{area } (\blacktriangle ABD)}{\text{area } (\blacktriangle ACD)} = \dfrac{BD}{CD}.\)
By Proposition 8.10 the triangles \(ABD\) and \(ACD\) have equal altitudes from \(D\). Applying Claim \(\PageIndex{1}\) again, we get that
\(\dfrac{\text{area } (\blacktriangle ABD)}{\text{area } (\blacktriangle ACD)} = \dfrac{AB}{AC}.\)
and hence the result.
Suppose \(ABC\) is a nondegenerate triangle and \(A'\) lies between \(B\) and \(C\). In this case the line segment \([AA']\) is called cevian (it is named after Giovanni Ceva and pronounced as chevian.) of \(\triangle ABC\) at \(A\). The second statement in the following exercise is called Ceva’s theorem.
Let \(ABC\) be a nondegenerate triangle. Suppose its cevians \([AA']\), \([BB']\) and \([CC']\) intersect at one point \(X\). Show that
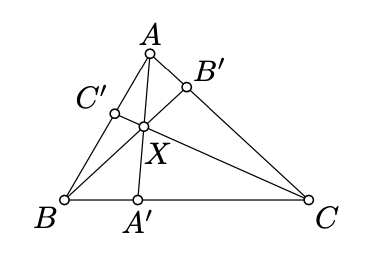
\(\begin{aligned} \frac{\text{area }(\blacktriangle ABX)}{\text{area }(\blacktriangle BCX)}&=\frac{AB'}{B'C}, \\ \frac{\text{area }(\blacktriangle BCX)}{\text{area }(\blacktriangle CAX)}&=\frac{BC'}{C'A}, \\ \frac{\text{area }(\blacktriangle CAX)}{\text{area }(\blacktriangle ABX)}&=\frac{CA'}{A'B} .\end{aligned}\)
Conclude that
\(\dfrac{AB'\cdot CA'\cdot BC'}{B'C\cdot A'B\cdot C'A}=1.\)
- Hint
-
Apply Claim \(\PageIndex{1}\) to show that
\(\dfrac{\text{area } (\blacktriangle ABB')}{\text{area } (\blacktriangle BCB')} = \dfrac{\text{area } (\blacktriangle AXB')}{\text{area } (\blacktriangle XCB')} = \dfrac{AB'}{B'C}\).
And observe that
\(\text{area } (\blacktriangle ABB') = \text{area } (\blacktriangle ABX) + \text{area } (\blacktriangle AXB')\),
\(\text{area } (\blacktriangle BCB') = \text{area } (\blacktriangle BCX) + \text{area } (\blacktriangle XCB')\).It implies the first identity; the rest is analogous.
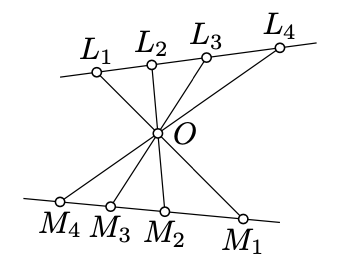
Suppose that points \(L_1\), \(L_2\), \(L_3\), \(L_4\) lie on a line \(\ell\) and points \(M_1\), \(M_2\), \(M_3\), \(M_4\) lie on a line \(m\). Assume that the lines \((L_1M_1)\), \((L_2M_2)\), \((L_3M_3)\), and \((L_4M_4)\) pass thru a point \(O\) that does not lie on \(\ell\) nor \(m\).
- Apply Claim \(\PageIndex{1}\) to show that \[\frac{\text{area }\blacktriangle OL_iL_j}{\text{area }\blacktriangle OM_iM_j}=\frac{OL_i\cdot OL_j}{OM_i\cdot OM_j}\] for any \(i\ne j\).
- Use (a) to prove that \[\frac{L_1L_2\cdot L_3L_4}{L_2L_3\cdot L_4L_1}=\frac{M_1M_2\cdot M_3M_4}{M_2M_3\cdot M_4M_1};\] that is, the quadruples \((L_1, L_2, L_3, L_4)\) and \((M_1, M_2, M_3, M_4)\) have the same cross ratio.
- Hint
-
To prove (a), apply Claim \(\PageIndex{1}\) twice to the triangles \(OL_iL_j, OL_jM_i\), and \(OM_iM_j\).
To prove part (b), use Claim \(\PageIndex{1}\) to rewrite the left hand side using the areas of triangles \(OL_1L_2, OL_2L_3, OL_3L_4\), and \(OL_4L_1\). Further use part (a) to rewrite it using areas of \(OM_1M_2, OM_2M_3,OM_3M_4\), and \(OM_4M_1\) and apply Claim \(\PageIndex{1}\) again to get the right hand side.

