2.2: The SAS Theorem

Last updated
Save as PDF

Page ID: 34125

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

We have said that two triangles are congruent if all their correspond ing sides and angles are equal, However in some cases, it is possible to conclude that two triangles are congruent, with only partial information about their sides and angles.

Suppose we are told that $\triangle ABC$ has $\angle A = 53^{\circ}$, $AB = 5$ inches, and $AC = 3$ inches. Let us attenpt to sketch $\triangle ABC$. We first draw an angle of $53^{\circ}$ with a protractor and label it $\angle A$. Using a ruler, we find the point 5 inches from the vertex on one side of the angle and label it $B$, On the other side of the angle, we find the point 3 inches from the vertex and label it $C$, See Figure $\PageIndex{1}$, There is now only one way for us to complete our sketch of $\triangle ABC$, and that is to connect points $B$ and $C$ with a line segment, We could now measure $BC$, $\angle B$, and $\angle C$ to find the remaining parts of the triangle.

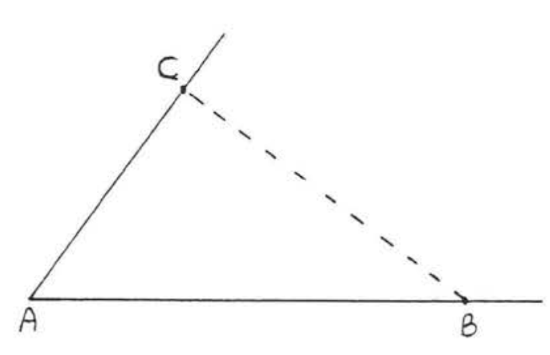
屏幕快照 2020-10-30 下午3.03.10.png — Figure $\PageIndex{1}$: Sketching $\triangle ABC$.

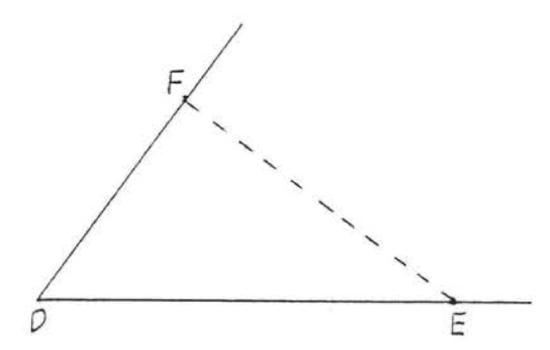
屏幕快照 2020-10-30 下午3.04.09.png — Figure $\PageIndex{2}$: Sketching $\triangle DEF$.

Suppose now $\triangle DEF$ were another triangle, with $\angle D = 53^{\circ}$, $DE = 5$ inches, and $DF = 3$ inches. We could sketch $\triangle DEF$ just as we did $\triangle ABC$, and then measure $EF$, $\angle E$, and $\angle F$ (Figure $\PageIndex{2}$). It is clear that we must have $BC = EF$, $\angle B = \angle E$, and $\angle C = \angle F$ because both triangles were drawn in exactly the same way. Therefore $\triangle ABC \cong \triangle DEF$.

In $\triangle ABC$, we say that $\angle A$ is the angle included between sides $AB$ and $AC$.
In $\triangle DEF$, we say that $\angle D$ is the angle included between sides $DE$ and $DF$.

Our discussion suggests the following theorem:

Theorem $\PageIndex{1}$ (SAS or Side-Angle-Side Theorem)

Two triangles are congruent if two sides and the included angle of one are equal respectively to two sides and the included angle of the other,

In Figure $\PageIndex{1}$ and $\PageIndex{2}$, $\triangle ABC \cong \triangle DEF$ because $AB, AC$, and $\angle A$ are equal respectively to $DE, DF$ and $\angle D$.

We sometimes abbreviate Theorem $\PageIndex{1}$ by simply writing $SAS = SAS$.

Example $\PageIndex{1}$

In $\triangle PQR$ name the angle included between sides

$PQ$ and $QR$,
$PQ$ and $PR$,
$PR$ and $QR$,

Solution

Note that the included angle is named by the letter that is common to both sides, For (1), the letter "$Q$" is common to $PQ$ and $QR$ and so $\angle Q$ is included between sides $PQ$ and $QR$. Similarly for (2) and (3).

Answer: (1) $\angle Q$, (2) $\angle P$, (3) $\angle R$.

Example $\PageIndex{2}$

For the two triangles in the diagram

list two sides and an included angle of each triangle that are respectively equal, using the infonnation given in the diagram,
write the congruence statement,

and (3) find $x$ by identifying a pair of corresponding sides of the congruent triangles.

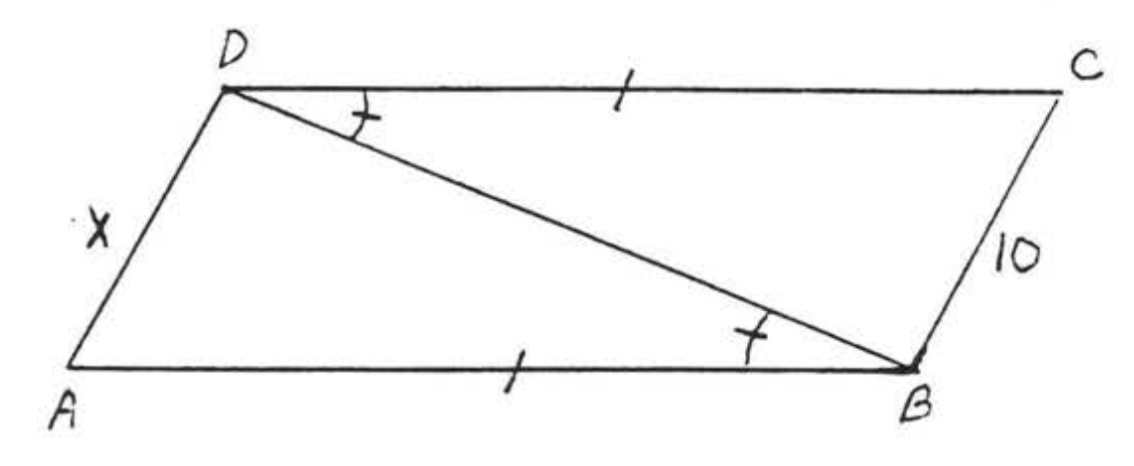
$屏幕快照 2020-10-30 下午3.17.42.png$

Solution

(1) The angles and sides that are marked the same way in the diagram are assumed to be equal, So $\angle B$ in $\triangle ABD$ is equal to $\angle D$ in $\triangle BCD$. Therefore, "$B$" corresponds to "$D$." We also have $AB = CD$. Therefore "$A$" must corresponds to "$C$". Thus, if the triangles are congruent, the correspondence must be

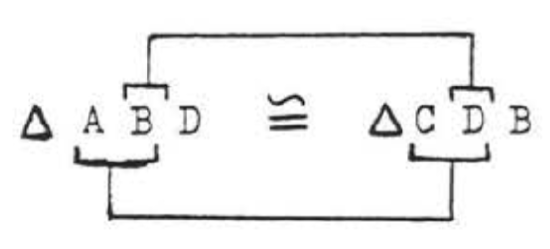
$屏幕快照 2020-10-30 下午3.21.21.png$

Finally, $BD$ (the same as $DB$) is a side common to both triangles, Summaryzing,

$\begin{array} {ccrclcl} {} & \ & {\underline{\triangle ABD}} & \ & {\underline{\triangle CDB}} & \ & {} \\ {\text{Side}} & \ & {AB} & = & {CD} & \ & {\text{(marked = in diagram)}} \\ {\text{Included Angle}} & \ & {\angle B} & = & {\angle D} & \ & {\text{(marked = in diagram)}} \\ {\text{Side}} & \ & {BD} & = & {DB} & \ & {\text{(common side)}} \end{array}$

(2) $\triangle ABD \cong \triangle CDB$ because of the SAS Theorem ($SAS = SAS$).

(3) $x = AD = CB = 10$ because $AD$ and $CB$ are corresponding sides (first and third letters in the congruence statement) a.~d corresponding sides of congruent triangles are equal.

Answer:

(1) $AB$, $\angle B$, $BD$ of $\triangle ABD = CD$, $\angle D$, $DB$ of $\triangle CDB$.

(2) $\triangle ABD \cong \triangle CDB$.

(3) $x = AD = CB = 10$.

Example $\PageIndex{3}$

For the two triangles in the diagram

list two sides and an included angle of each triangle that are respectively equal, using the information given in the diagram.
write the congruence statement, and
find $x$ and $y$ by identifying a pair of corresponding sides of the congruent triangles.

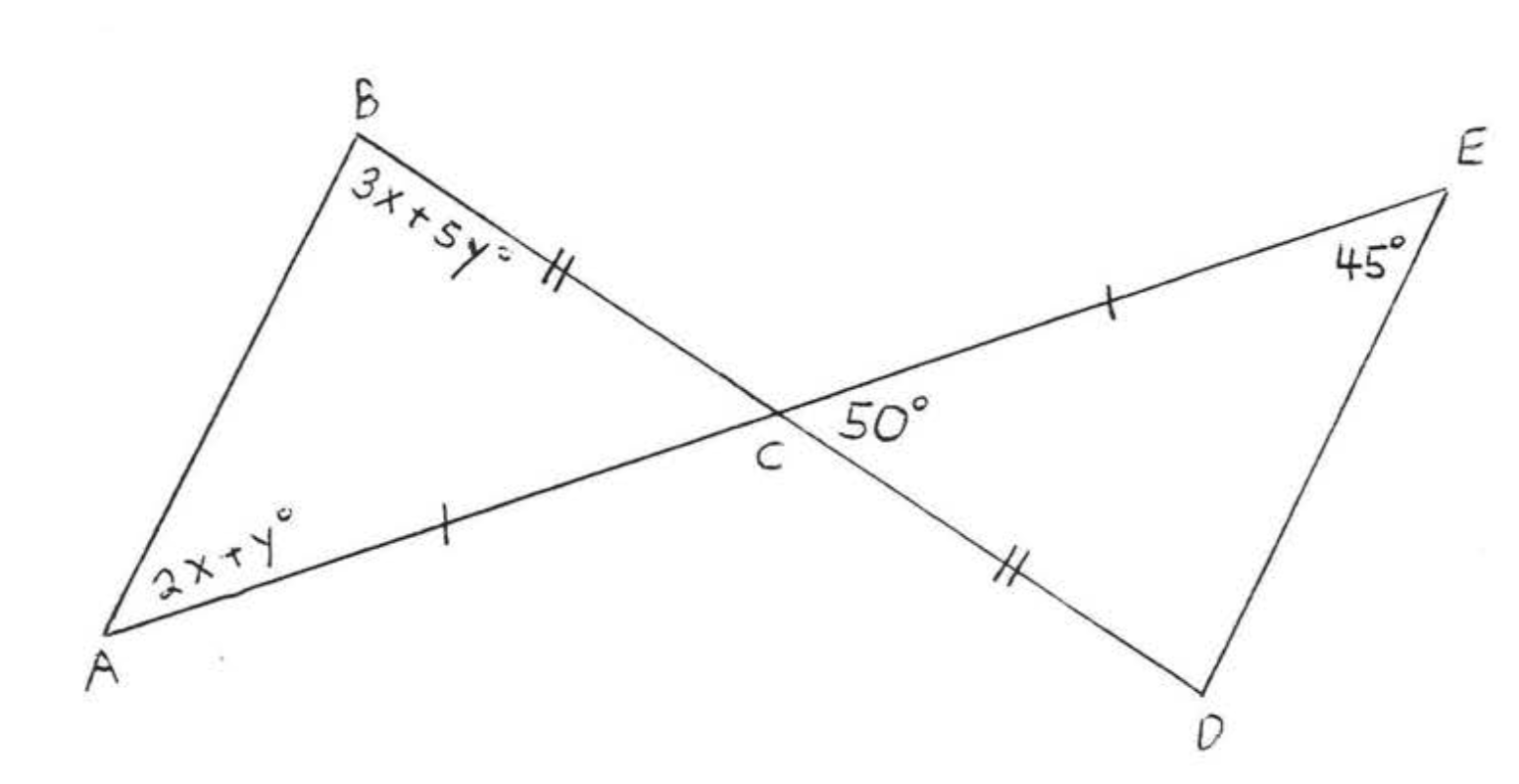
$屏幕快照 2020-10-30 下午3.34.32.png$

Solution

(1) $AC = CE$ and $BC = CD$ because they are mar!,;:ed the same way. We also know that $\angle ACB = \angle ECD = 50^{\circ}$ because vertical angles are equal. Therefore "$C$" in $\triangle ABC$ corresponds to "$C$" in $\triangle CDE$. Since $AC = CE$, we must have that "$A$" in $\triangle ABC$ corresponds to "$E$" in $\triangle CDE$. Thus, if the triangles are congruent, the correspondence must be

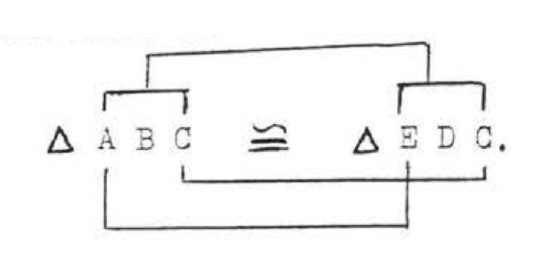
$屏幕快照 2020-10-30 下午3.41.57.png$

We summarize:

$\begin{array} {ccrclcl} {} & \ & {\underline{\triangle ABC}} & \ & {\underline{\triangle EDC}} & \ & {} \\ {\text{Side}} & \ & {AC} & = & {EC} & \ & {\text{(marked = in diagram)}} \\ {\text{Included Angle}} & \ & {\angle ACB} & = & {\angle ECD} & \ & {\text{(vertical angles are =)}} \\ {\text{Side}} & \ & {BC} & = & {DC} & \ & {\text{(marked = in diagram)}} \end{array}$

(2) $\triangle ABC \cong \triangle EDC$ because of the SAS theorem. ($SAS = SAS$)

(3) $\angle A = \angle E$ and $\angle B = \angle D$ because they are corres:9onding angles of the congruent triangles. $\angle D = 85^{\circ}$ because the sum of the angles of $\triangle EDC$ must be $180^{\circ}$. ($\angle D = 180^{\circ} - (50^{\circ} + 45^{\circ}) = 180^{\circ} - 95^{\circ} = 85^{\circ}$). We obtain a system of two equations in the two unknowns $x$ and $y$:

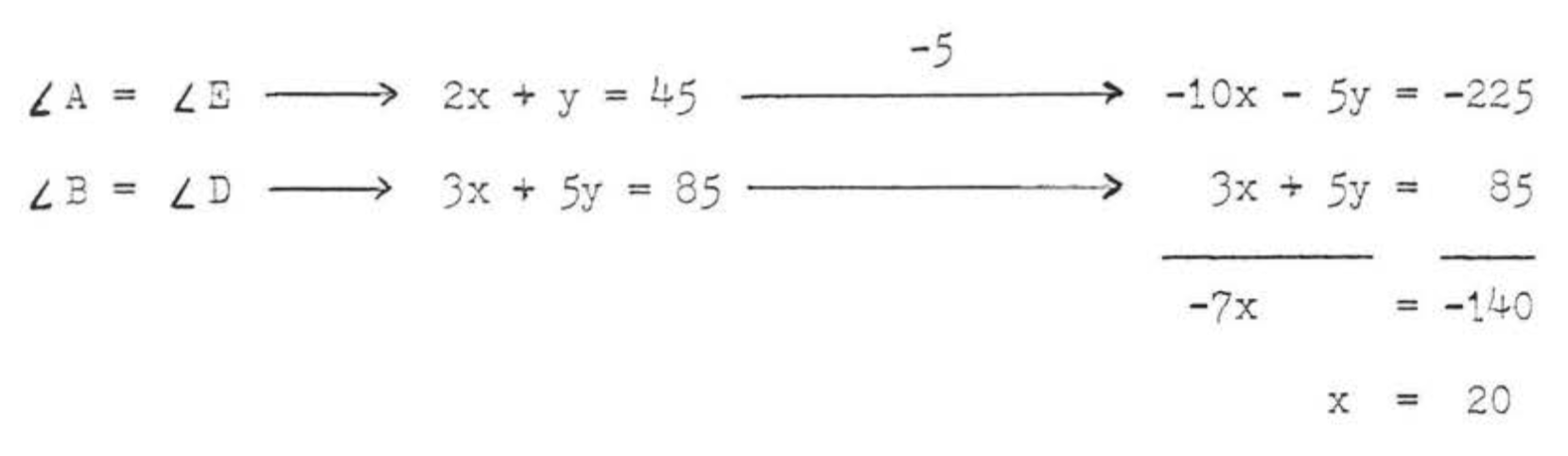
$屏幕快照 2020-10-30 下午3.46.35.png$

Substituting for $x$ in the first original equation,

\[\begin{array} {rcl} {2x + y} & = & {45} \\ {2(20) + y} & = & {45} \\ {40 + y} & = & {45} \\ {y} & = & {45- 40} \\ {y} & = & {5} \end{array}\]

Check:

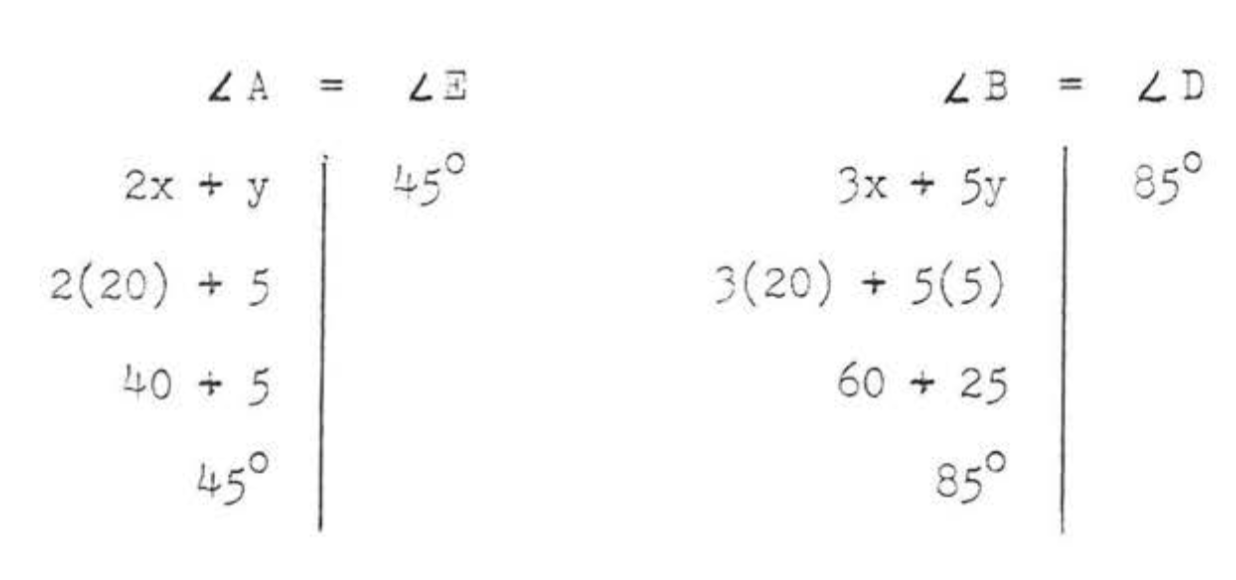
$屏幕快照 2020-10-30 下午3.50.00.png$

Answer:

$AC$, $\angle ACB$, $BC$ of $\triangle ABC$ = $EC, \angle ECD, DC$ of $\triangle EDC$.
$\triangle ABC \cong \triangle EDC$.
$x = 20, y = 5$.

Example $\PageIndex{4}$

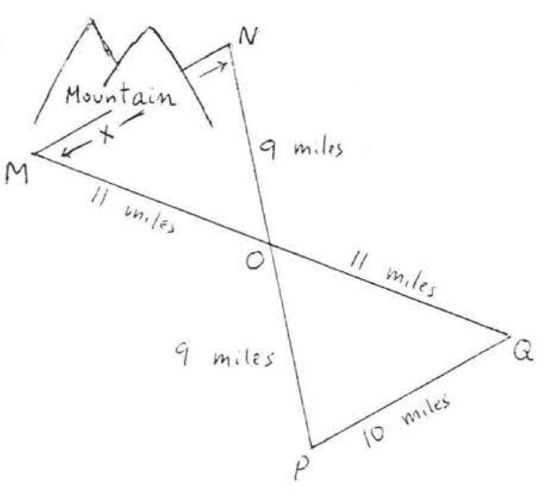
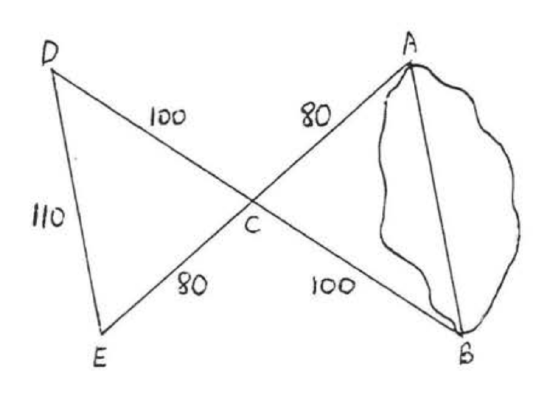
The following procedure was used to measure the d.istance AB across a pond: From a point $C$, $AC$ and $BC$ were measured and found to be 80 and 100 feet respectively. Then $AC$ was extended to $E$ so that $AC = CE$ and $BC$ was extended to $D$ so that $BC = CD$. Finally, $DE$ we found to be 110 feet.

Write the congruence statement.
Give a reason for (1).
Find $AB$.

$屏幕快照 2020-10-30 下午3.55.21.png$

Solution

(1) $\angle ACB = \angle ECD$ because vertical angles are equal. Therefore the "$C$'s" correspond, $AC = EC$ so $A$ must correspond to $E$. We have

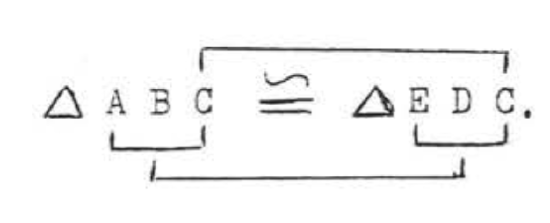
$屏幕快照 2020-10-30 下午3.56.25.png$

(2) $SAS = SAS$. Sides $AC$, $BC$, and included angle $C$ of $ABC$ are equal respectively to $EC, DC$, and included angle $C$ of $\angle EDC$.

(3) $AB = ED$ ecause they are corresponding sides of congruent triangles, Since $ED = 110$, $AB = 110$.

Answer

(1) $\triangle ABC \cong \triangle EDC$.

(2) $SAS = SAS$: $AC$, $\angle C$, $BC$ of $\triangle ABC = EC$, $\angle C$, $DC$ of $\triangle EDC$.

(3) $AB = 110 feet$.

Historical Note

The SAS Theorem is Proposition 4 in Euclid's Elements, Both our discussion and Suclit's proof of the SAS Theoremimplicitly use the following principle: If a geometric construction is repeated in a different location (or what amounts to the same thing is "moved" to a different location) then the size and shape of the figure remain the same, There is evidence that Euclid used this principle reluctantly, and many mathematicians have since questioned its use in formal proofs, They feel that it makes too strong an assumption about the nature of physical space and is an inferior form of geometric reasoning. Bertrand Russell (1872 - 1970), for example, has suggested that we would be better off assuming the SAS Theorem as a postulate, This is in fact done in a system of axioms for Euclidean geometry devised by David Hilbert (1862 - 1943), a system that has gained much favor with modern mathematicians. Hilbert was the leading exponent of the "formalist school," which sought to discover exactly what assumptions underlie each branch of mathematics and to remove all logical ambiguities, Hilbert's system, however, is too formal for an introductory course in geometry,

Problems

1 - 4. For each of the following (1) draw the triangle with the two sides and the included angle and (2) measure the remaining side and angles:

1. $AB = 2$ inches, $AC = 1$ inch, $\angle A = 60^{\circ}$.

2. $DE = 2$ inches, $DF = 1$ inch, $\angle D = 60^{\circ}$.

3. $AB = 2$ inches, $AC = 3$ inches, $\angle A = 40^{\circ}$.

4. $DE = 2$ inches, $DF = 3$ inches, $\angle D = 40^{\circ}$.

5 - 8. Name the angle included between sides

5. $AB$ and $BC$ in $\triangle ABC$.

6. $XY$ and $YZ$ in $\triangle XYZ$.

7. $DE$ and $DF$ in $\triangle DEF$.

8. $RS$ and $TS$ in $\triangle RST$.

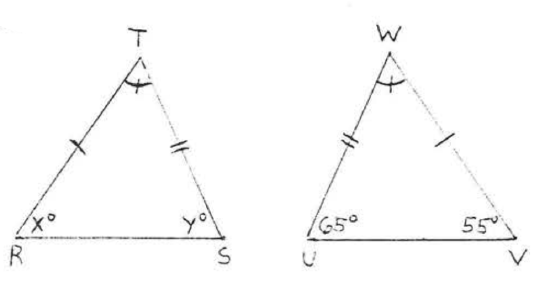
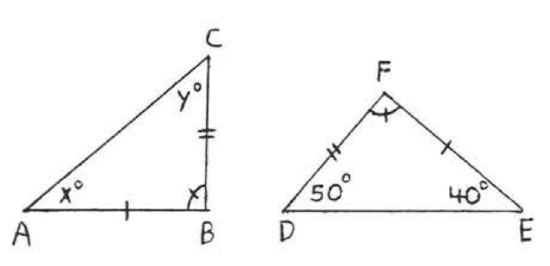
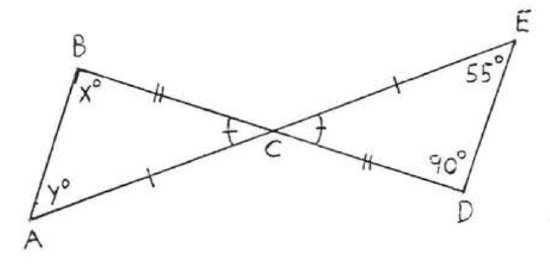
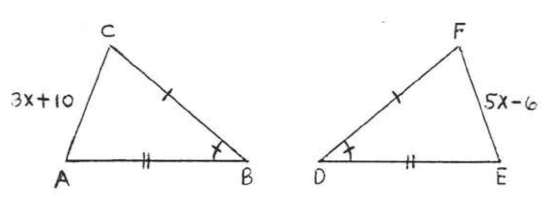
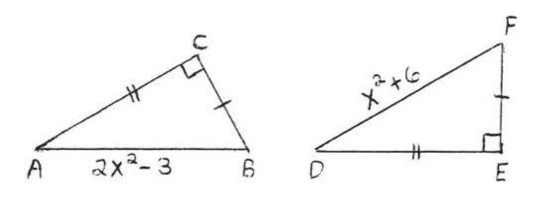
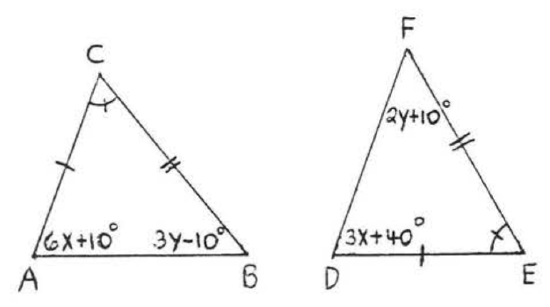
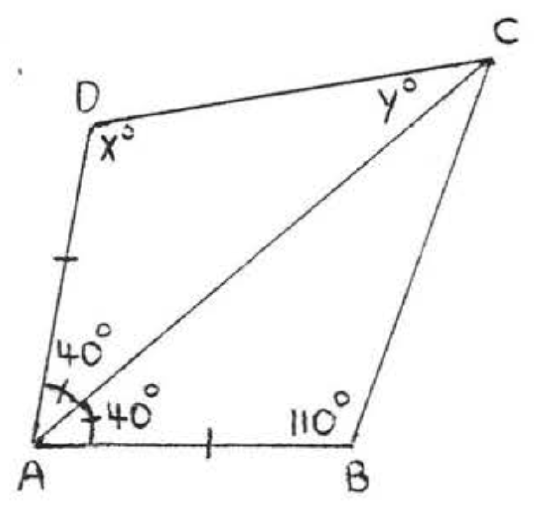
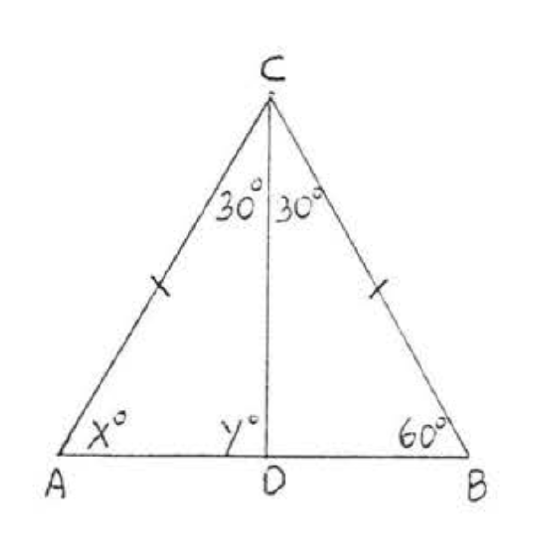
9 - 22. For each of the following.

(1) list two sides and an included angle of each triangle that are respectively equal, using the information given in the diagram,

(2) write the congruence statement,

(3) find $x$, or $x$ and $y$.

Assume that angles or sides marked in the same way are eQual.

9. $Screen Shot 2020-10-30 at 4.15.31 PM.png$ 10. $Screen Shot 2020-10-30 at 4.15.53 PM.png$

11. $Screen Shot 2020-10-30 at 4.16.11 PM.png$ 12. $Screen Shot 2020-10-30 at 4.16.32 PM.png$

13. $Screen Shot 2020-10-30 at 4.16.58 PM.png$ 14. $Screen Shot 2020-10-30 at 4.17.13 PM.png$

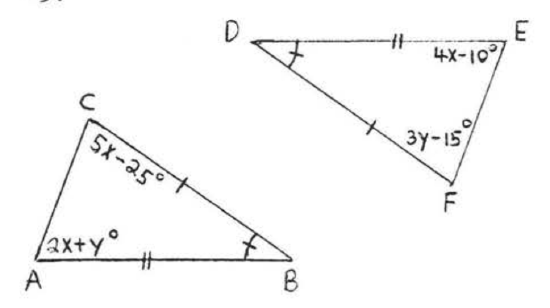15. $Screen Shot 2020-10-30 at 4.17.29 PM.png$ 16. $Screen Shot 2020-10-30 at 4.17.50 PM.png$

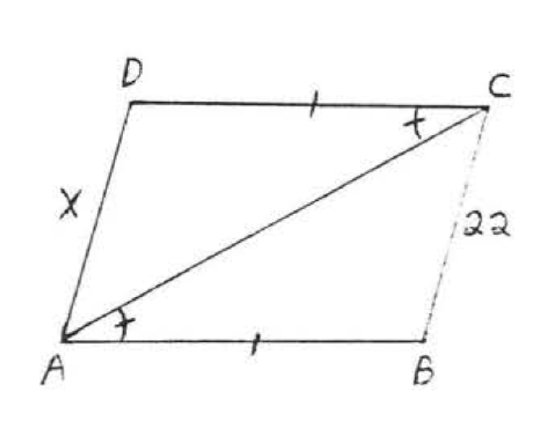17. $Screen Shot 2020-10-30 at 4.18.18 PM.png$ 18. $Screen Shot 2020-10-30 at 4.18.32 PM.png$

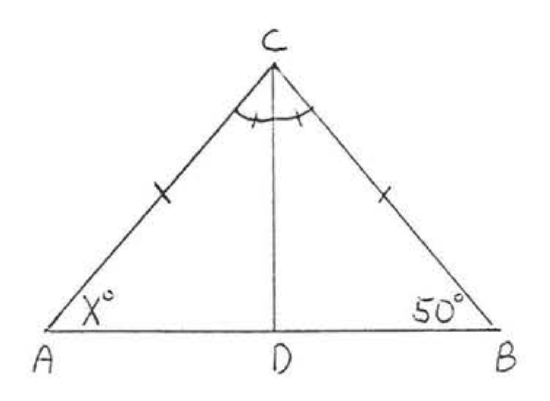19. $Screen Shot 2020-10-30 at 4.18.53 PM.png$ 20. $Screen Shot 2020-10-30 at 4.19.05 PM.png$

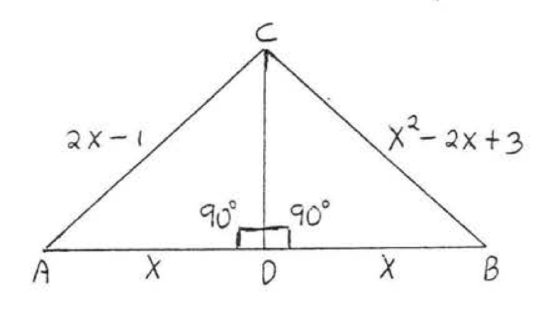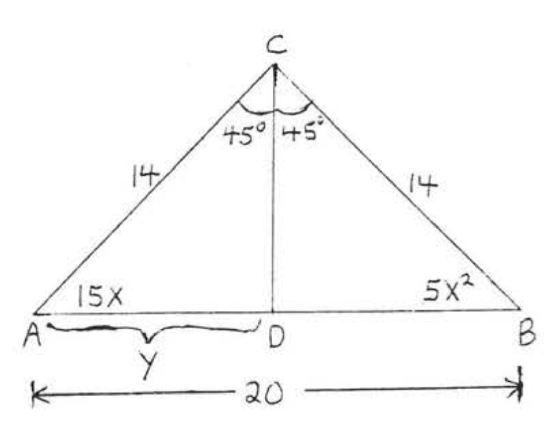
21. $Screen Shot 2020-10-30 at 4.19.25 PM.png$ 22. $Screen Shot 2020-10-30 at 4.19.41 PM.png$

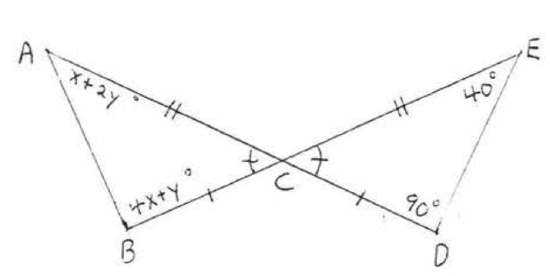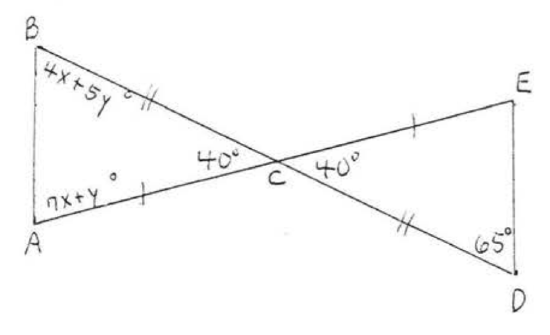
23. $Screen Shot 2020-10-30 at 4.20.09 PM.png$ 24. $Screen Shot 2020-10-30 at 4.20.34 PM.png$

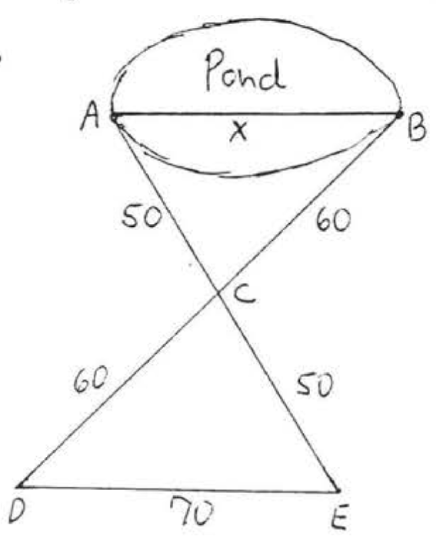25. $Screen Shot 2020-10-30 at 4.21.03 PM.png$ 26. $Screen Shot 2020-10-30 at 4.21.22 PM.png$

Search

Text Color

Text Size

Margin Size

Font Type

Theorem \(\PageIndex{1}\) (SAS or Side-Angle-Side Theorem)

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Example \(\PageIndex{3}\)

Example \(\PageIndex{4}\)

Historical Note

Problems