3.2: Problem Set 3

Unless otherwise stated, assume all of the axioms of neutral geometry (albeit unstated) and the global form of the Hyperbolic Parallel Postulate (HPP) as well; i.e., assume hyperbolic geometry.

1. Prove that the sum of the interior angles of any triangle is less than two right angles \(\left(180^{\circ}\right)\).
2. Don’t assume the HPP but do assume that there is one triangle for which the sum of the interior angles is less than \(180^{\circ}\). Prove the local form of the HPP.
3. Don’t assume the HPP but do assume that there is one pair of parallel lines that share a transversal that forms a pair of non-congruent alternate interior angles. Prove the local form of the HPP.
4. Prove that the summit of a Saccheri quadrilateral is never a boundary (limit) parallel to its base.
5. Prove that a side of a Lambert quadrilateral is never a boundary (limit) parallel to its opposite side.
6. Prove that two lines do not share more than one common perpendicular (i.e., no "railroad track ties").

In Exs 7-10, consider the Poincaré model of hyperbolic geometry in Euclidean geometry determined by the circle of radius 2 centered at the origin \(\mathrm{O}(0,0)\) of the Cartesian plane, \(\gamma=\left\{(\mathrm{x}, \mathrm{y}) \mid \mathrm{x}^{2}+\mathrm{y}^{2}<2^{2}\right\}\)

7. Find the equation for the circle \(\delta\) that determines the right boundary (limit) parallel to the \(\mathrm{x}\)-axis on the point \(\mathrm{P}(1,1)\) and accurately sketch the situation.

[Hint: The center of this circle must lie on the line \(x=2\). Why? Recall the equation of the circle with center \(\mathrm{C}(\mathrm{h}, \mathrm{k})\) and radius \(\mathrm{r}: \delta=\left\{(\mathrm{x}, \mathrm{y}) \mid(\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{r}^{2}\right.\).]

9. Redo Ex 7 for the left boundary parallel at the same point \(P(1,1)\).
10. Make an accurate sketch of the situation in Exs 7 and 8 and "sketch in" the Poincaré line on \(P(1,1)\) that is perpendicular to the \(\mathrm{x}\)-axis.
11. Find the equation for the Euclidean circle \(\delta\) of the Poincaré line in Ex 9 . [Hint: For orthogonality with the \(\mathrm{x}\)-axis, its center \(\mathrm{C}\) will have to be on the \(\mathrm{x}\)-axis, say \((c, 0)\), so \((\mathrm{x}-\mathrm{c})^{2}+\mathrm{y}^{2}=\mathrm{r}^{2}\) is the equation and it passes through \(\mathrm{P}(1,1)\). The needed additional condition is orthogonality with the defining circle. This can easily be done by using the Pythagorean Theorem with the radii and distance between the centers, \(|c|\)
12. Consider the Poincaré model of hyperbolic geometry in Euclidean geometry determined by the circle of radius 4 centered at the origin \(\mathrm{O}(0,0)\) of the Cartesian plane, \(\gamma=\left\{(\mathrm{x}, \mathrm{y}) \mid \mathrm{x}^{2}+\mathrm{y}^{2}<4^{2}\right\}\). Find the equation for the Euclidean circle \(\delta\) of the Poincaré line determined by the points \(\mathrm{A}(1,2)\) and \(\mathrm{B}(3,0)\).

[Hint: For its equation, \(\delta=\left\{(\mathrm{x}, \mathrm{y}) \mid(\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{r}^{2}\right.\), orthogonality with the defining circle can be involved using Pythagorean theorem: \(4^{2}+r^{2}=h^{2}+k^{2}\) so that \(r^{2}=h^{2}+k^{2}-4^{2}\). The perpendicular bisector of Euclidean segment AB has slope 1, passes through the midpoint, \(\mathrm{M}(2,1)\), and (h, k).] 12. The idea of Ex 11 can be generalized to provide an analytic proof (See Chapt. 4) of Axiom 1 as a Euclidean geometry theorem as one step in the proof that the Poincaré model really is a model for hyperbolic geometry entirely within Euclidean geometry (establishing "relative consistency" of the hyperbolic geometry axioms (see Chapter 5 for a trivial synthetic proof!). Consider the Poincaré model determined by the circle of radius \(\mathrm{R}\) centered at the origin \(\mathrm{O}(0,0)\) of the Cartesian plane, \(\gamma=\left\{(\mathrm{x}, \mathrm{y}) \mid \mathrm{x}^{2}+\mathrm{y}^{2}<\mathrm{R}^{2}\right\}\).

Find the equation for the Euclidean circle \(\delta\) of the Poincaré line determined by two general Poincaré points \(\mathrm{A}\left(\mathrm{a}_{\mathrm{x}}, \mathrm{a}_{\mathrm{y}}\right)\) and \(\mathrm{B}\left(\mathrm{b}_{\mathrm{x}}, \mathrm{b}_{\mathrm{y}}\right)\) where \(\mathrm{A}, \mathrm{B}\), and \(\mathrm{O}\) are not collinear.

That is, if \((\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{r}^{2}\) is its equation, express \(\mathrm{h}, \mathrm{k}\), and r uniquely in terms of \(\mathrm{R}\) and the coordinates of \(A\) and B. Orthogonality with the defining circle can be involved using the Pythagorean theorem:

\(\mathrm{R}^{2}+\mathrm{r}^{2}=\mathrm{h}^{2}+\mathrm{k}^{2}\) so that \(\mathrm{r}^{2}=\mathrm{h}^{2}+\mathrm{k}^{2}-\mathrm{R}^{2}\). The perpendicular bisector of Euclidean segment AB has to pass through its midpoint \(\mathrm{M}\) and the center of the circle \(\mathrm{C}(\mathrm{h}, \mathrm{k})\). Three cases occur with the most general being that Euclidean line \(A B\) is neither vertical nor horizontal. In that case, calculate the equation of the perpendicular bisector, \(\mathrm{y}=\mathrm{mx}+\mathrm{b}\) with \(\mathrm{m}\) being the negative reciprocal of the slope of line AB and using \(M\) to calculate b. Since \(C\) is on that line, we have \(k=m h+b\) and, substituting in the coordinates of either A or \(\mathrm{B}\) that must lie on the circle, we will have \((\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{r}^{2}=\mathrm{h}^{2}+\mathrm{k}^{2}-\mathrm{R}^{2}\) entirely in terms of \(\mathrm{h}(\) and the given coefficients). Luckily, the terms involving \(h^{2}\) cancel out and we can solve uniquely for h, then \(\mathrm{k}=\mathrm{mh}+\mathrm{b}\), and finally \(\mathrm{r}^{2}=\mathrm{h}^{2}+\mathrm{k}^{2}-\mathrm{R}^{2}\). That is, there is one and only one such circle. The other two cases use same idea but are easier.

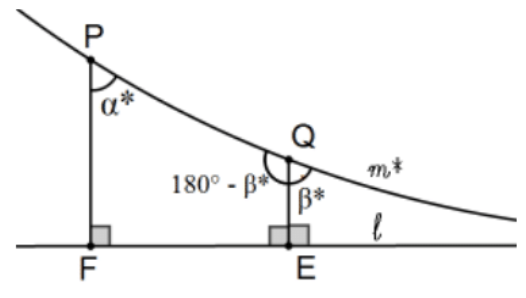
13. Prove that angles of parallelism strictly increase along boundary parallels in the direction of boundedness.

[Hint: The given figure says it all: \(\alpha^{*}+\left(180-\beta^{*}\right)<180^{\circ}\) because PQEF is a quadrilateral.]

A polygon can be circumscribed if there is a circle, called the circumcircle, that contains every vertex of the polygon. It should be obvious that a polygon can be circumscribed iff there is a point equidistant from each of its vertices.

14. Prove that a Lambert quadrilateral can never be circumscribed. [Hint: Assume that there is a circumcircle and derive a contradiction; i.e., use proof by contradiction. Note: Do not assume that the intersection of the diagonals is the center of the assumed circumcircle but you may use the fact that it would have to have a center.]

15. Construct the circumcircle of a Saccheri quadrilateral. [Hint: Construct the perpendicular bisectors of a leg and the base and prove that the intersection is equidistant from each of the vertices, hence the center of the circumcircle.]
16. Complete the proof that the triangles of the last theorem of the chapter are genuine triangles and that they cannot be circumscribed. [Why does the presentation fail in Euclidean geometry?]
17. Show by a careful sketch in the Poincaré plane that not all triangles can be circumscribed and argue why it cannot be circumscribed. A Poincaré argument? A Euclidean argument?

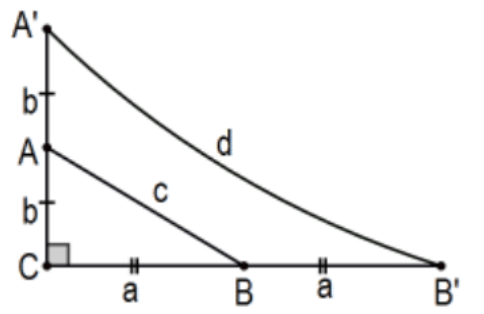
18. Prove that the Pythagorean Theorem fails by showing that if \(\triangle \mathrm{ABC}\) is a right triangle with \(\mathrm{a}^{2}+\mathrm{b}^{2}=\mathrm{c}^{2}\), then a right triangle with legs of 2a and \(2 \mathrm{~b}\) does not satisfy the Pythagorean equation.

[Hint: Consider the associated Saccheri quadrilateral with summit A \({ }^{\prime} \mathrm{B}^{\prime}\).]

19. Prove the Summit Theorem.

20. Theorem: If two Saccheri quadrilaterals have congruent bases and congruent summits, then they are congruent. [That is, prove it.]

In Ex 21-24, assume that A and B are points inside the fixed Euclidian circle \(\gamma\) that defines the Poincaré disk model for hyperbolic geometry, \(\delta\) is the orthogonal circle determined by A and \(\mathrm{B}\), and \(\mathrm{P}\) and \(\mathrm{Q}\) are the points of intersection of the circles \(\gamma\) and \(\delta\). Recall that Poincaré distance between points A and B (the measure of Poincaré line segment AB) is:

\[m_{p}(A B)=d_{p}(A, B)=|\ln (A, B ; P, Q)|=\left |\ln \left(\frac{A P / P B}{A Q / Q B} \right) \right|= \left| \ln \left(\frac{(A P)(Q B)}{(A Q)(P B)}\right) \right|. \nonumber\]

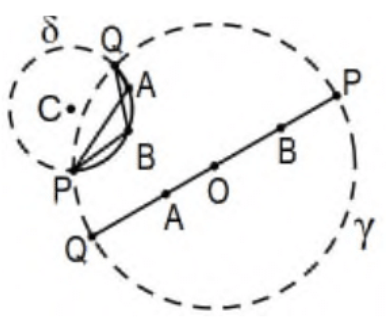
where \(P\) and \(Q\) are determined by the Poincaré line determined by \(A\) and \(B\).

21. Prove that the Poincaré distance is independent of which point is labeled P and which one is Q.

22. Prove that \(d_{p}(A, B)=d_{p}(B, A)\).
23. Prove that \(d_{p}(A, B)=0\) iff \(A=B\).
24. Prove that if \(A, B\), and \(C\) are collinear points in the Poincaré model, \(d_{p}(A, B)+d_{p}(B, C)=d_{p}(A, C)\) iff \(\mathrm{B}\) is between A and C; that is, between them on the Poincaré portion of the (same) Euclidean circle determined by any two of the points.

[Note 1: Don’t overlook the most important detail, the fact that \(|\mathrm{x}|+|\mathrm{y}|\) is not necessarily equal to \(|\mathrm{x}+\mathrm{y}|\) only " \(\geq\). You must first confirm that, in any situation you use it, equality holds.]

[Note 2: The full notion of "betweenness" requires that, for B to be between A and C, this equation holds without the assumption that the points be collinear. This is true for Poincaré measures of line segments but the proof is much more difficult. See Chapter 5 , concluding with PS 5, #8.]

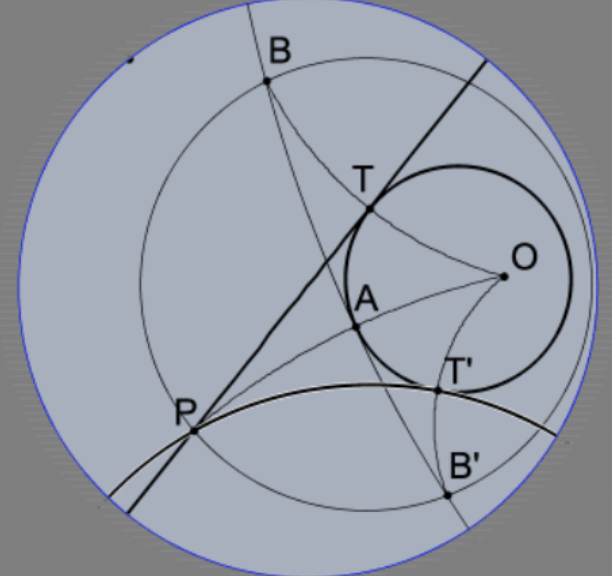
25. Assuming that the Poincaré disk model really is a model for hyperbolic geometry, recall the construction for the tangents from a point P outside of circle O given in PS 2, #28, and explain the indicated construction of tangent lines \(\mathrm{PT}\) and \(\mathrm{PT}^{\prime}\) to the Poincaré circle (O; OA) (i.e., center \(\mathrm{O}\) of radius OA) in the pictured Poincaré disk model (assuming a "Poincaré compass" and "Poincaré straightedge") and prove that the construction is valid. [Note1: Eventually, we’ll include a construction of the Poincaré tangents using the "Euclidean tools" (much easier to come by!) but that is much harder. Note 2: The steps of the most well-known construction of these tangents in Euclidean geometry can be carried out with a Poincaré compass and straightedge in the Poincaré disk model but the result is not correct. In other words, proofs matter!]

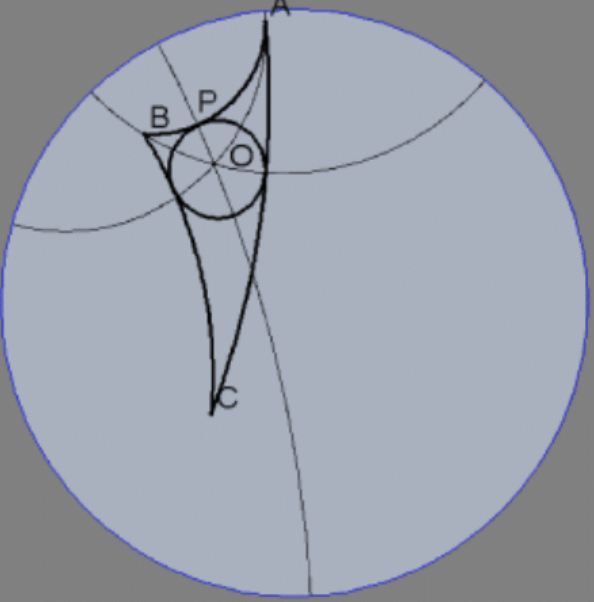
26. Assuming that the Poincaré disk model really is a model for hyperbolic geometry, recall the construction for the incircle of a triangle from Chapter 2 (neutral geometry). Explain the indicated construction of the incircle of the given triangle in the pictured Poincaré disk model and prove that it is valid.

[Note: As with Ex. 25, the pictured construction uses a Poincaré compass and straightedge but it is possible to construct the incircle of a Poincaré triangle with Euclidean compass and straightedge but it is exceedingly tedious.]

27a. The segment \(\mathrm{A}_{1} \mathrm{~B}_{1}=[0,1]=\{\mathrm{x} \in \mathbf{R} \mid 0 \leq \mathrm{x} \leq 1\}\) has Euclidean measure 1 (surprise, surprise). Confirm that its Poincaré measure is \(\ln (3)\) in the Poincaré model determined by \(\gamma=(\mathrm{O} ; 2)\) by explaining this computation:

\(\mathrm{m}_{f}([0,1])=\left|\ln \left(\frac{\mathrm{AP} / \mathrm{PB}}{\mathrm{AQ} / \mathrm{QB}}\right)\right|=\left|\ln \left(\frac{2 / 1}{2 / 3}\right)\right|=\left|\ln \left(\frac{3}{1}\right)\right|=|\ln (3)|=\ln (3)\)

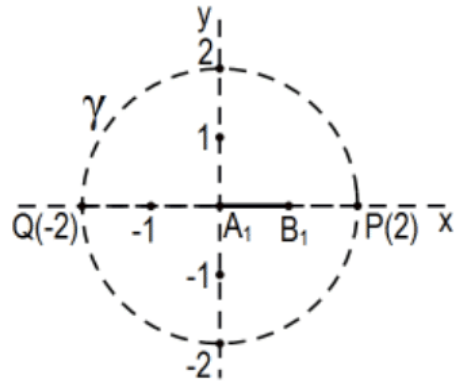
27b. Do the same for segment \(\mathrm{A}_{2} \mathrm{~B}_{2}=[1,3 / 2]\); that is, calculate both its Euclidean and Poincaré measures.

27c. Do the same for segment \(\mathrm{A}_{3} \mathrm{~B}_{3}=[3 / 2,7 / 4]\).

27d. Do the same for segment \(A_{n} B_{n}=\left[\left(2^{n-1}-1\right) / 2^{n-2},\left(2^{n}-1\right) / 2^{n-1}\right]\).

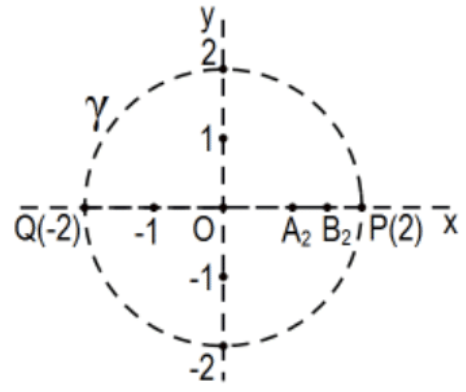
What is the limit as \(n \rightarrow \infty\) ?

Note: Segments of the type \([0,1]\) in #27a above are especially easy to compute:

Let \([0, x]\) be the Euclidean segment along the \(x\)-axis that is also a segment in the Poincaré model defined by circle \(\gamma=(\mathrm{O} ; \mathrm{R})\), segment AB in the figure, \(0<\mathrm{x}<\mathrm{R}\). Clearly, its Euclidean measure is just \(\mathrm{x}\). For its Poincaré measure: [Here we take account of direction as well as positive Euclidean length.]

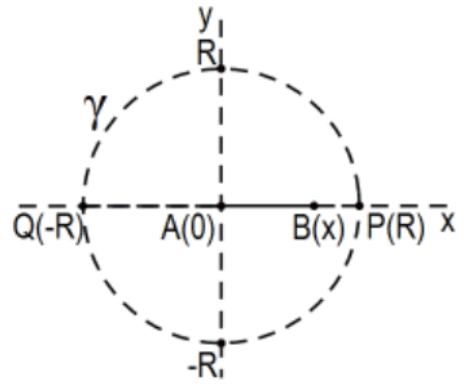
\[\mathrm{m}_{f}([0, \mathrm{x}])=\left|\ln \left(\frac{\mathrm{AP} / \mathrm{PB}}{\mathrm{AQ} / \mathrm{QB}}\right)\right|=\left|\ln \left(\frac{\mathrm{R} /(\mathrm{x}-\mathrm{R})}{-\mathrm{R} /(\mathrm{R}+\mathrm{x})}\right)\right|=\left|\ln \left(\frac{\mathrm{R}+\mathrm{x}}{\mathrm{R}-\mathrm{x}}\right)\right|=\ln \left(\frac{\mathrm{R}+\mathrm{x}}{\mathrm{R}-\mathrm{x}}\right) \nonumber\]

Note: The last expression makes it clear that, as \(\mathrm{x}\) approaches \(\mathrm{R}\), the length of segment [A(0), \(\mathrm{B}(\mathrm{x})]\) becomes infinite (as it must). In Chapter 5 (PS 5, #5), we will see that by an easy isometric (congruence) transformation, the Poincaré measure of any Poincaré segment in a Poincaré model in the \(\mathrm{x}\),y-coordinate (Cartesian) plane can be computed in this convenient manner, no simultaneous solution of two quadratic equations in two variables (to find the coordinates of the defining points \(P\) and \(Q\), and no Euclidean distance formula computations required.