Skip to main content
\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)
Mathematics LibreTexts

3.2: Graphical Solutions

  1. Last updated
  2. Save as PDF
  • Page ID
    1813

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Before giving a more general algorithm for handling this problem and problems like it, we note that when the number of variables is small (preferably 2), a graphical technique can be used.

    Inequalities, such as the four given in Pablo's problem, are often called \(\textit {constraints}\), and values of the variables that satisfy these constraints comprise the so-called \(\textit {feasible region}\). Since there are only two variables, this is easy to plot:

    Example 35: Constraints and feasible region

    Pablo's constraints are

    \begin{eqnarray*}
    &x\geq 5&\\
    &y\geq 7&\\[2mm]
    &15\leq x+y\leq25\, .&
    \end{eqnarray*}

    Plotted in the \((x,y)\) plane, this gives:

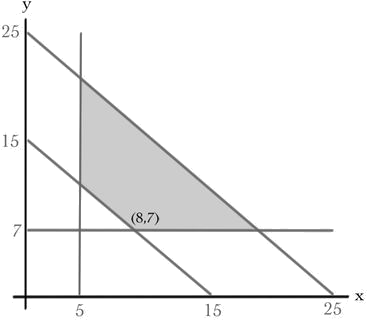
    Figure 1.png

    You might be able to see the solution to Pablo's problem already. Oranges are very sugary, so they should be kept low, thus \(y=7\). Also, the less fruit the better, so the answer had better lie on the line \(x+y=15\). Hence, the answer must be at the vertex \((8,7)\). Actually this is a general feature of linear programming problems, the optimal answer must lie at a vertex of the feasible region. Rather than prove this, lets look at a plot of the linear function \(s(x,y)=5x+10y\).

    Example 36: The sugar function

    Plotting the sugar function requires three dimensions:


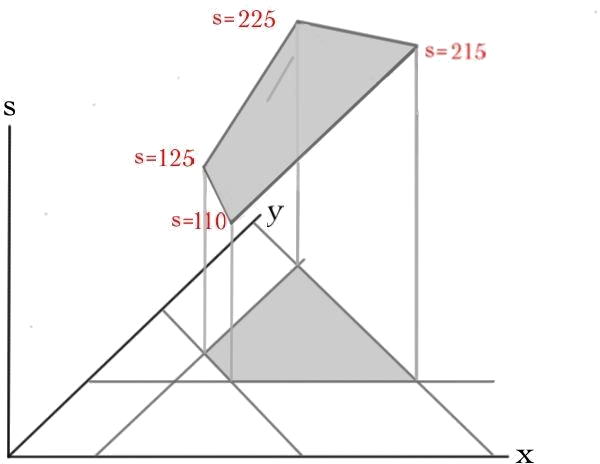
    Figure 2.png

    The plot of a linear function of two variables is a plane through the origin. Restricting the variables to the feasible region gives some lamina in 3-space. Since the function we want to optimize is linear (and assumedly non-zero), if we pick a point in the middle of this lamina, we can always increase/decrease the function by moving out to an edge and, in turn, along that edge to a corner. Applying this to the above picture, we see that Pablo's best option is 110 grams of sugar a week, in the form of 8 apples and 7 oranges.

    It is worthwhile to contrast the optimization problem for a linear function with the non-linear case you may have seen in calculus courses:

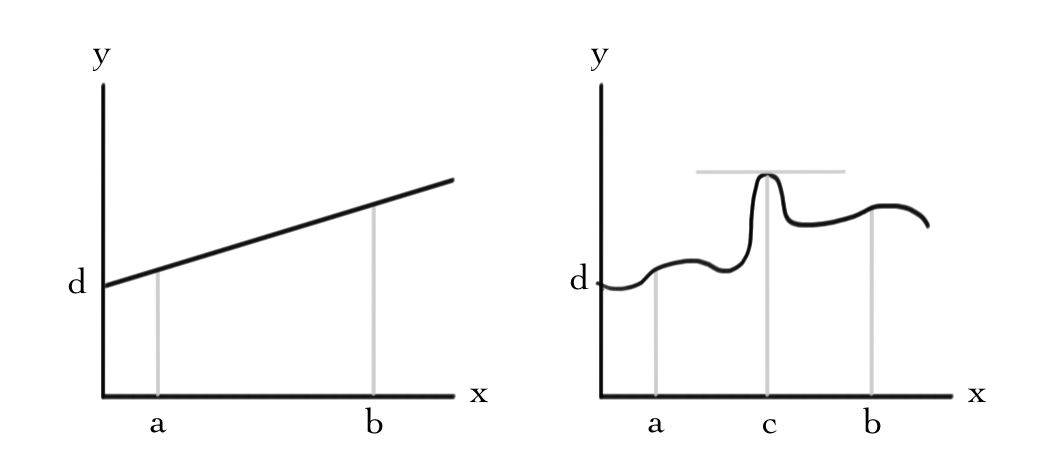
    Here we have plotted the curve \(f(x)=d\) in the case where the function \(f\) is linear and non-linear. To optimize \(f\) in the interval \([a,b]\), for the linear case we just need to compute and compare the values \(f(a)\) and \(f(b)\). In contrast, for non-linear functions it is necessary to also compute the derivative \(\frac{\mathrm{d} f}{\mathrm{d} x}\) to study whether there are extrema inside the interval.

    Contributor