5.1: Sets and Operations on Sets

Before beginning this section, it would be a good idea to review sets and set notation, including the roster method and set builder notation, in Section 2.3.

PREVIEW ACTIVITY $\PageIndex{1}$: Set Operations

In Section 2.1, we used logical operators (conjunction, disjunction, negation) to form new statements from existing statements. In a similar manner, there are several ways to create new sets from sets that have already been defined. In fact, we will form these new sets using the logical operators of conjunction (and), disjunction (or), and negation (not). For example, if the universal set is the set of natural numbers $N$ and

$$A = \{1, 2, 3, 4, 5, 6\} \quad \text{ and } \quad B = \{1, 3, 5, 7, 9\},$$

• The set consisting of all natural numbers that are in $A$ and are in $B$ is the set $\{1, 3, 5\}$;
• The set consisting of all natural numbers that are in $A$ or are in $B$ is the set $\{1, 2, 3, 4, 5, 6, 7, 9\}$; and
• The set consisting of all natural numbers that are in $A$ and are not in $B$ is the set $\{2, 4, 6\}.$

These sets are examples of some of the most common set operations, which are given in the following definitions.

Definition: intersection

Let $A$ and $B$ be subsets of some universal set $U$. The intersection of $A$ and $B$, written $A \cap B$ and read “$A$ intersect $B$,” is the set of all elements that are in both $A$ and $B$. That is,

$$A \cap B = \{x \in U \, | \, x \in A \text{ and } x \in B\}.$$

The union of $A$ and $B$, written $A \cup B$ and read “$A$ union $B$,” is the set of all elements that are in $A$ or in $B$. That is,

$$A \cup B = \{x \in U \, | \, x \in A \text{ or } x \in B\}.$$

Definition: complement

Let $A$ and $B$ be subsets of some universal set $U$. The set difference of $A$ and $B$, or relative complement of $B$ with respect to $A$, written $A -B$ and read “$A$ minus $B$” or “the complement of $B$ with respect to $A$,” is the set of all elements in $A$ that are not in $B$. That is,

$$A - B = \{x \in U \, | \, x \in A \text{ and } x \notin B\}.$$

The complement of the set $A$, written $A^c$ and read “the complement of $A$,” is the set of all elements of $U$ that are not in $A$. That is,

$$A^c = \{x \in U \, | \, x \notin A\}.$$

For the rest of this preview activity, the universal set is $U = \{0, 1, 2, 3, ..., 10\}$, and we will use the following subsets of $U$:

$$A = \{0, 1, 2, 3, 9\} \quad \text{ and } \quad B = \{2, 3, 4, 5, 6\},$$

So in this case, $A \cap B = \{x \in U \, | \, x \in A \text{ and } x \in B\} = \{2, 3\}.$ Use the roster method to specify each of the following subsets of $U$.

1. $A \cup B$
2. $A^c$
3. $B^c$

We can now use these sets to form even more sets. For example,

$$A \cap B^c = \{0, 1, 2, 3, 9\} \cap \{0, 1, 7, 8, 9, 10\} = \{0, 1, 9\}.$$

Use the roster method to specify each of the following subsets of $U$.

4. $A \cup B^c$
5. $A^c \cap B^c$
6. $A^c \cup B^c$
7. $(A \cap B)^c$

Preview Activity $\PageIndex{2}$: Venn Diagrams for Two Sets

In Preview Activity $\PageIndex{1}$, we worked with verbal and symbolic definitions of set operations. However, it is also helpful to have a visual representation of sets. Venn diagrams are used to represent sets by circles (or some other closed geometric shape) drawn inside a rectangle. The points inside the rectangle represent the universal set $U$, and the elements of a set are represented by the points inside the circle that represents the set. For example, Figure $\PageIndex{1}$ is a Venn diagram showing two sets.

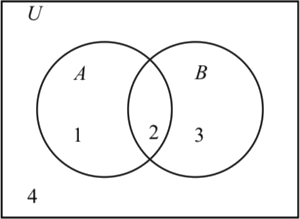
Figure $\PageIndex{1}$: Venn Diagram for Two Sets

In Figure $\PageIndex{1}$, the elements of $A$ are represented by the points inside the left circle, and the elements of $B$ are represented by the points inside the right circle. The four distinct regions in the diagram are numbered for reference purposes only. (The numbers do not represent elements in a set.) The following table describes the four regions in the diagram.

Region	Elements of $U$	Set
1	In $A$ and not in $B$	$A - B$
2	In $A$ and in $B$	$A \cap B$
3	In $B$ and not in $A$	$B - A$
4	Not in $A$ and not in $B$	$A^c \cap B^c$

We can use these regions to represent other sets. For example, the set $A \cup B$ is represented by regions 1, 2, and 3 or the shaded region in Figure $\PageIndex{2}$.

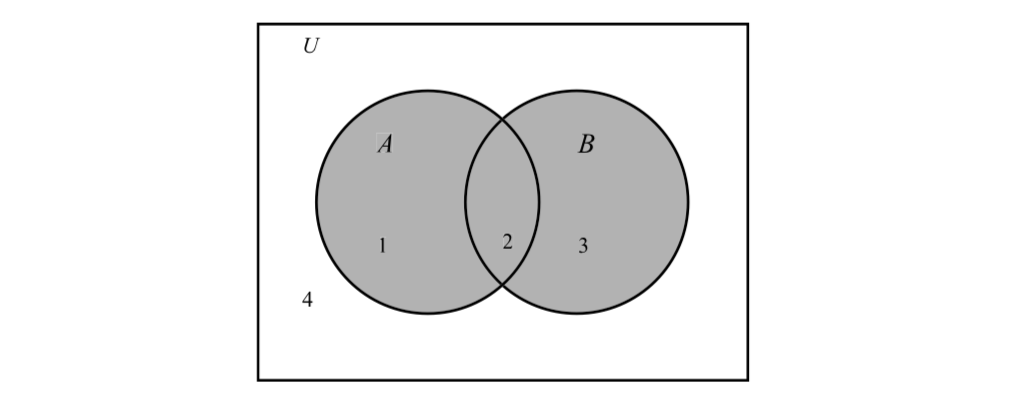
Figure $\PageIndex{2}$: Venn Diagram for $A \cup B$

Let $A$ and $B$ be subsets of a universal set $U$. For each of the following, draw a Venn diagram for two sets and shade the region that represent the specified set. In addition, describe the set using set builder notation.

1. $A^c$
2. $B^c$
3. $A^c \cup B$
4. $A^c \cup B^c$
5. $(A \cap B)^c$
6. $(A \cup B) - (A \cap B)$

Set Equality, Subsets, and Proper Subsets

In Section 2.3, we introduced some basic definitions used in set theory, what it means to say that two sets are equal and what it means to say that one set is a subset of another set. We need one more definition.

Definition: proper subset

Let $A$ and $B$ be two sets contained in some universal set $U$. The set $A$ is a proper subset of $B$ provided that $A \subseteq B$ and $A \ne B$. When $A$ is a proper subset of $B$, we write $A \subset B$.

One reason for the definition of proper subset is that each set is a subset of itself. That is,

If $A$ is a set, then $A \subseteq A$

However, sometimes we need to indicate that a set $X$ is a subset of $Y$ but $X \ne Y$. For example, if

$X = \{1, 2\}$ and $Y = \{0, 1, 2, 3\}.$

then $X \subset Y$. We know that $X \subseteq Y$ since each element of $X$ is an element of $Y$, but $X \ne Y$ since $0 \in Y$ and $0 \notin X$. (Also, $3 \in Y$ and $3 \notin X$.) Notice that the notations $A \subset B$ and $A \subseteq B$ are used in a manner similar to inequality notation for numbers ($a < b$ and $a \le b$).

It is often very important to be able to describe precisely what it means to say that one set is not a subset of the other. In the preceding example, $Y$ is not a subset of $X$ since there exists an element of $Y$ (namely, 0) that is not in $X$.

In general, the subset relation is described with the use of a universal quantifier since $A \subseteq B$ means that for each element $x$ of $U$, if $x \in A$, then $x \in B$. So when we negate this, we use an existential quantifier as follows:

$$\begin{array} {rcl} {A \subseteq B} &\text{means} & {(\forall x \in U)[(x \in A) \to (x \in B)].} \\ {A \not\subseteq B} &\text{means} & {\urcorner(\forall x \in U)[(x \in A) \to (x \in B)]} \\ {} & & {(\exists x \in U) \urcorner [(x \in A) \to (x \in B)]} \\ {} & & {(\exists x \in U) [(x \in A) \wedge (x \notin B)].} \end{array}$$

So we see that $A \not\subseteq B$ means that there exists an $x$ in $U$ such that $x \in A$ and $x \notin B$.

Notice that if $A = \emptyset$, then the conditional statement, “For each $x \in U$, if $x \in \emptyset$, then $x \in B$” must be true since the hypothesis will always be false. Another way to look at this is to consider the following statement:

$\emptyset \not\subseteq B$ means that there exists an $x \in \emptyset$ such that $x \notin B$.

However, this statement must be false since there does not exist an $x$ in $\emptyset$. Since this is false, we must conclude that $\emptyset \subseteq B$. Although the facts that $\emptyset \subseteq B$ and $B \subseteq B$ may not seem very important, we will use these facts later, and hence we summarize them in Theorem 5.1.

Theorem 5.1

For any set $B$, $\emptyset \subseteq B$ and $B \subseteq B$.

In Section 2.3, we also defined two sets to be equal when they have precisely the same elements. For example,

$\{x \in \mathbb{R} \, | \, x^ = 4\} = \{-2, 2\}$.

If the two sets $A$ and $B$ are equal, then it must be true that every element of $A$ is an element of $B$, that is, $A \subseteq B$, and it must be true that every element of $B$ is an element of $A$, this is, $B \subseteq A$. Conversely, if $A \subseteq B$ and $B \subseteq A$, then $A$ and $B$ must have precisely the same elements. This gives us the following test for set equality:

Theorem 5.2

Let $A$ and $B$ be subsets of some universal set $U$. Then $A = B$ if and only if $A \subseteq B$ and $B \subseteq A$.

Progress Check 5.3: Using Set Notation

Let the universal set be $U = \{1, 2, 3, 4, 5, 6\}$, and let

$A = \{1, 2, 4\}$, $B = \{1, 2, 3, 5\}$, $C = \{x \in U \, | \, x^2 \le 2\}$.

In each of the following, fill in the blank with one or more of the symbols $\subset$, $\subseteq$, =, $\ne$, $\in$ or $\notin$ so that the resulting statement is true. For each blank, include all symbols that result in a true statement. If none of these symbols makes a true statement, write nothing in the blank.

$$\begin{array} {rclrcl} {A} &\text{_____________} & {B\quad \quad \quad } {\emptyset} &\text{_____________}& {A} \\ {5} &\text{_____________} & {B\quad \quad \ \ \ } {\{5\}} &\text{_____________} & {B} \\ {A} &\text{_____________} & {C\quad \ \ \ \ \ \ } {\{1, 2\}} &\text{_____________} & {C} \\ {\{1, 2\}} &\text{_____________} & {A\quad \ \ \ } {\{4, 2, 1\}} &\text{_____________} & {A} \\ {6} &\text{_____________} & {A\quad \quad \quad } {B} &\text{_____________} & {\emptyset} \end{array} \nonumber$$

Answer

Add texts here. Do not delete this text first.

More about Venn Diagrams

In Preview Activity $\PageIndex{2}$, we learned how to use Venn diagrams as a visual representation for sets, set operations, and set relationships. In that preview activity, we restricted ourselves to using two sets. We can, of course, include more than two sets in a Venn diagram. Figure $\PageIndex{3}$ shows a general Venn diagram for three sets (including a shaded region that corresponds to $A \cap C$).

In this diagram, there are eight distinct regions, and each region has a unique reference number. For example, the set A is represented by the combination of regions 1, 2, 4, and 5, whereas the set C is represented by the combination of regions 4, 5, 6, and 7. This means that the set $A \cap C$ is represented by the combination of regions 4 and 5. This is shown as the shaded region in Figure $\PageIndex{3}$.

Finally, Venn diagrams can also be used to illustrate special relationships be- tween sets. For example, if $A \subseteq B$, then the circle representing $A$ should be completely contained in the circle for $B$. So if $A \subseteq B$, and we know nothing about

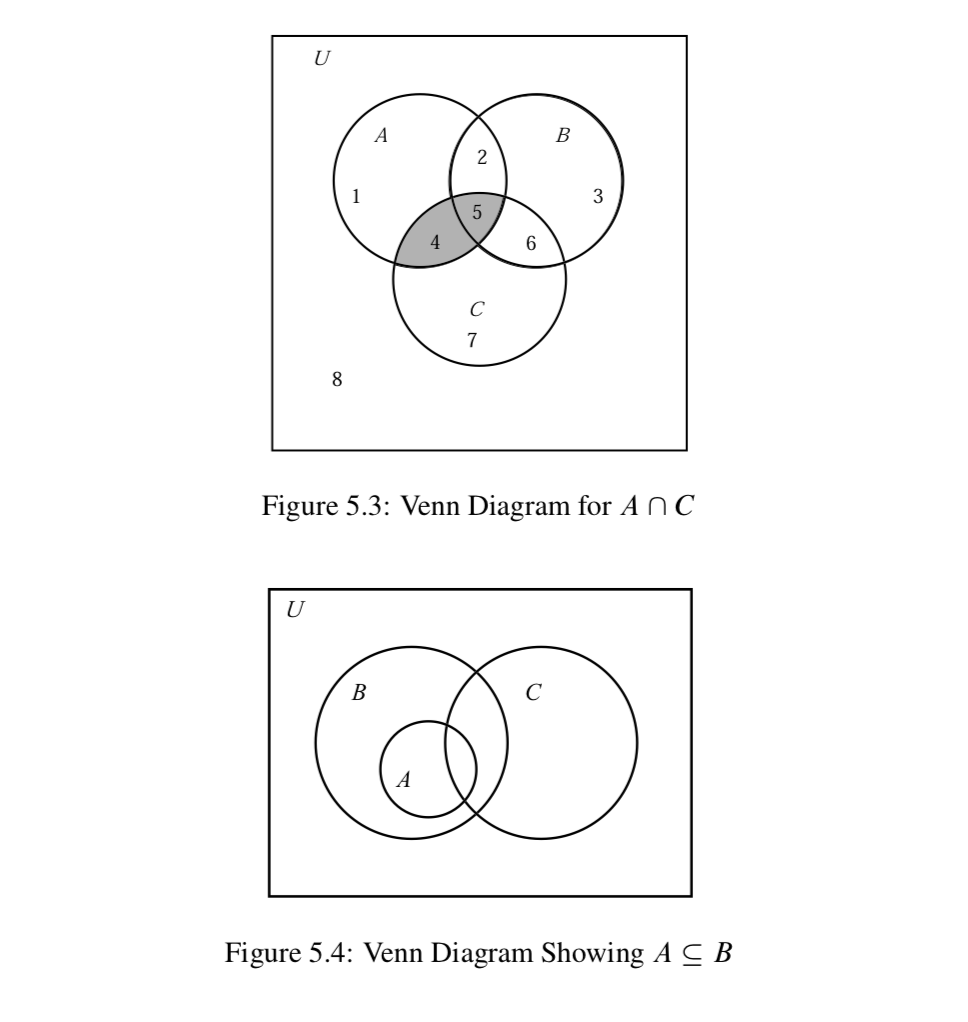
any relationship between the set $C$ and the sets $A$ and $B$, we could use the Venn diagram shown in Figure $\PageIndex{4}$.

Progress Check 5.4: Using Venn Diagrams

Let $A$, $B$, and $C$ be subsets of a universal set $U$.

1. For each of the following, draw a Venn diagram for three sets and shade the region(s) that represent the specified set.
   
   (a) $(A \cap B) \cap C$
   (b) $(A \cap B) \cup C$
   (c) $(A^c \cup B)$
   (d) $A^c \cap (B \cup C)$
2. Draw the most general Venn diagram showing $B \subseteq (A \cup C)$.
3. Draw the most general Venn diagram showing $A \subseteq (B^c \cup C)$.

Answer

Add texts here. Do not delete this text first.

The Power Set of a Set

The symbol 2 is used to describe a relationship between an element of the universal set and a subset of the universal set, and the symbol $\subseteq$ is used to describe a relationship between two subsets of the universal set. For example, the number 5 is an integer, and so it is appropriate to write $5 \in \mathbb{Z}$. It is not appropriate, however, to write $5 \subseteq \mathbb{Z}$ since 5 is not a set. It is important to distinguish between 5 and {5}. The difference is that 5 is an integer and {5} is a set consisting of one element. Consequently, it is appropriate to write $\{5\} \subseteq \mathbb{Z}$, but it is not appropriate to write $\{5\} \in \mathbb{Z}$. The distinction between these two symbols (5 and {5}) is important when we discuss what is called the power set of a given set.

Definition: power set

If $A$ is a subset of a universal set $U$, then the set whose members are all the subsets of $A$ is called the power set of $A$. We denote the power set of $A$ by $\mathcal{P}(A)$. Symbolically, we write

$\mathcal{P}(A) = \{X \subseteq U \, | \, X \subseteq A\}.$

That is, $X \in \mathcal{P}(A)$ if and only if $X \subseteq A$.

When dealing with the power set of $A$, we must always remember that $\emptyset \subseteq A$ and $A \subseteq A$. For example, if $A = \{a, b\}$, then the subsets of $A$ are

$$\emptyset, \{a\}, \{b\}, \{a,b\}.$$

We can write this as

$\mathcal{P}(A) = \{\emptyset, \{a\}, \{b\}, \{a,b\}\}.$

Now let $B = \{a, b, c\}$. Notice that $B = A \cup \{c\}$. We can determine the subsets of $B$ by starting with the subsets of $A$ in (5.1.10). We can form the other subsets of $B$ by taking the union of each set in (5.1.10) with the set $\{c\}$. This gives us the following subsets of $B$.

$$\{c\}, \{a, c\}, \{b, c\}, \{a, b, c\}.$$

So the subsets of $B$ are those sets in (5.1.10) combined with those sets in (5.1.11). That is, the subsets of $B$ are

$$\emptyset, \{a\}, \{b\}, \{a,b\}, \{c\}, \{a, c\}, \{b, c\}, \{a, b, c\},$$

which means that

$\mathcal{P}(B) = \{\emptyset, \{a\}, \{b\}, \{a,b\}, \{c\}, \{a, c\}, \{b, c\}, \{a, b, c\}\}.$

Notice that we could write

$\{a, c\} \subseteq B$ or that $\{a, c\} \in \mathcal{P}(B)$.

Also, notice that $A$ has two elements and $A$ has four subsets, and $B$ has three elements and $B$ has eight subsets. Now, let $n$ be a nonnegative integer. The following result can be proved using mathematical induction. (See Exercise 17).)

Theorem 5.5.

Let $n$ be a nonnegative integer and let $T$ be a subset of some universal set. If the set $T$ has $n$ elements, then the set $T$ has $2^n$ subsets. That is, $\mathcal{P}(T)$ has $2^n$ elements.

The Cardinality of a Finite Set

In our discussion of the power set, we were concerned with the number of elements in a set. In fact, the number of elements in a finite set is a distinguishing characteristic of the set, so we give it the following name.

Definition: cardinality

The number of elements in a finite set $A$ is called the cardinality of $A$ and is denoted by card($A$)

Example

card($\emptyset$) = 0;

card({$a$, $b$}) = 2

card($\mathcal{P}(\{a, b\})$) = 4

Theoretical Note: There is a mathematical way to distinguish between finite and infinite sets, and there is a way to define the cardinality of an infinite set. We will not concern ourselves with this at this time. More about the cardinality of finite and infinite sets is discussed in Chapter 9.

Standard Number Systems

We can use set notation to specify and help describe our standard number systems. The starting point is the set of natural numbers, for which we use the roster method.

$\mathbb{N} = \{1, 2, 3, 4, ...\}$

The integers consist of the natural numbers, the negatives of the natural numbers, and zero. If we let $\mathbb{N} ^- = \{..., -4, -3, -2, -1\}$, then we can use set union and write

$\mathbb{Z} = \mathbb{N} ^- \cup \{0\} \cup \mathbb{N}$.

So we see that $\mathbb{N} \subseteq \mathbb{Z}$, and in fact, $\mathbb{N} \subset \mathbb{Z}$.

We need to use set builder notation for the set $\mathbb{Q}$ of all rational numbers, which consists of quotients of integers.

$\mathbb{Q} = \Big\{\dfrac{m}{n}\ |\ m, n \in \mathbb{Z} \text{and } n \ne 0\Big\}$

Since any integer $n$ can be written as $n = \dfrac{n}{1}$, we see that $\mathbb{Z} \subseteq \mathbb{Q}$.

We do not yet have the tools to give a complete description of the real numbers. We will simply say that the real numbers consist of the rational numbers and the irrational numbers. In effect, the irrational numbers are the complement of the set of rational numbers $\mathbb{Q}$ in $\mathbb{R}$. So we can use the notation $\mathbb{Q} ^c = \{x \in \mathbb{R}\ |\ x \notin \mathbb{Q}\}$ and write

$\mathbb{R} = \mathbb{Q} \cup \mathbb{Q} ^c$ and $\mathbb{Q} \cap \mathbb{Q} ^c = \emptyset$.

A number system that we have not yet discussed is the set of complex numbers. The complex numbers, $\mathbb{C}$, consist of all numbers of the form $a + bi$, where $a, b \in \mathbb{R}$ and $i = \sqrt{-1}$ (or $i^2 = -1$). That is,

$\mathbb{C} = \{a + bi\ |\ a,b \in \mathbb{R} \text{and } i = sqrt{-1}\}.$

We can add and multiply complex numbers as follows: If $a, b, c, d \in \mathbb{R}$, then

$$\begin{array} {rcl} {(a + bi) + (c + di)} &= & {(a + c) + (b + d)i, \text{ and}} \\ {(a + bi)(c + di)} &= & {ac + adi + bci + bdi^2} \\ {} &= & {(ac - bd) + (ad + bc)i.} \end{array}$$

Exercises for Section 5.1

1. Assume the universal set is the set of real numbers. Let
   
   $A = \{-3, -2, 2, 3\}.$
   $B = \{x \in \mathbb{R}\ |\ x^2 = 4 \text{ or } x^2 = 9\},$
   $C = \{x \in \mathbb{R}\ |\ x^2 + 2 = 0\},$
   $D = \{x \in \mathbb{R}\ |\ x > 0\}.$
   
   Respond to each of the following questions. In each case, explain your answer.
   
   (a) Is the set $A$ equal to the set $B$?
   (b) Is the set $A$ a subset of the set $B$?
   (c) Is the set $C$ equal to the set $D$?
   (d) Is the set $C$ a subset of the set $D$?
   (e) Is the set $A$ a subset of the set $D$?
2. (a) Explain why the set $\{a, b\}$ is equal to the set $\{b, a\}$.
   (b) Explain why the set $\{a, b, b, a, c\}$ is equal to the set $\{b, c, a\}$.
3. Assume that the universal set is the set of integers. Let
   
   $A = \{-3, -2, 2, 3\}.$
   $B = \{x \in \mathbb{Z}\ |\ x^2 \le 9\},$
   $C = \{x \in \mathbb{Z}\ |\ x \ge -3\},$
   $D = \{1, 2, 3, 4\},$
   
   In each of the following, fill in the blank with one or more of the symbols $\subset$, $\subseteq$, $\not\subseteq$, $=$, $\ne$, $\in$ or $\notin$ so that the resulting statement is true. For each blank, include all symbols that result in a true statement. If none of these symbols makes a true statement, write nothing in the blank.
   $$\begin{array} {rclrcl} {A} &\text{_____________} & {B\quad \quad \quad \ \ \ \ \ } {\emptyset} &\text{_____________}& {A} \\ {5} &\text{_____________} & {C\quad \quad \quad \ \ } {\{5\}} &\text{_____________} & {C} \\ {A} &\text{_____________} & {C\quad \quad \ \ \ \ \ } {\{1, 2\}} &\text{_____________} & {B} \\ {\{1, 2\}} &\text{_____________} & {A\quad \quad \ \ } {\{3, 2, 1\}} &\text{_____________} & {D} \\ {4} &\text{_____________} & {B\quad \quad \quad \ \ \ \ \ } {D} &\text{_____________} & {\emptyset} \\ {\text{card} (A)} &\text{_____________} & {\text{card} (D)\quad \ } {\text{card} (A)} &\text{_____________} & {\text{card} (B)} \\ {A} &\text{_____________} & {\mathcal{P}(A)\quad \quad \quad } {A} &\text{_____________} & {\mathcal {P} (B)} \end{array}$$
4. Write all of the proper subset relations that are possible using the sets of numbers $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, and $\mathbb{R}$.
5. For each statement, write a brief, clear explanation of why the statement is true or why it is false.
   
   (a) The set $\{a, b\}$ is a subset of $\{a, c, d, e\}$.
   (b) The set $\{-2, 0, 2\}$ is equal to $\{x \in \mathbb{Z} \, | \, x$ is even and $x^2 < 5\}.$
   (c) The empty set $\emptyset$ is a subset of $\{1\}.$
   (d) If $A = \{a, b\}$, then the set $\{a\}$ is a subset of $\mathcal{P} (A)$.
6. Use the definitions of set intersection, set union, and set difference to write useful negations of these definitions. That is, complete each of the following sentences
   
   (a) $x \notin A \cap B$ if and only if ... .
   (b) $x \notin A \cup B$ if and only if ... .
   (c) $x \notin A - B$ if and only if ... .
7. Let $U = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\},$ and let
   
   $A = \{3, 4, 5, 6, 7\}$
   $B = \{1, 5, 7, 9\}$
   $C = \{3, 6, 9\}$
   $D = \{2, 4, 6, 8\}$

   Use the roster method to list all of the elements of each of the following sets.
   (a) $A \cap B$
   (b) $A \cup B$
   (c) $(A \cup B)^c$
   (d) $A^c \cap B^c$
   (e) $(A \cup B) \cap C$
   (f) $A \cap C$
   (g) $B \cap C$
   (h) $(A \cap C) \cup (B \cap C)$
   (i) $B \cap D$
   (j) $(B \cap D)^c$
   (k) $A - D$
   (l) $B - D$
   (m) $(A - D) \cup (B - D)$
   (n) $(A \cup B) - D$

8. Let $U = \mathbb{N}$, and let
   
   $A =\{x \in \mathbb{N}\ |\ x \ge 7\},$
   $B =\{x \in \mathbb{N}\ |\ x \text{ is odd}\},$
   $C =\{x \in \mathbb{N}\ |\ x \text{ is a multiple of } 3\},$
   $D =\{x \in \mathbb{N}\ |\ x \text{ is even}\},$
   
   Use the roster method to list all of the elements of each of the following sets.
   
   (a) $A \cap B$
   (b) $A \cup B$
   (c) $(A \cup B)^c$
   (d) $A^c \cap B^c$
   (e) $(A \cup B) \cap C$
   (f) $(A \cap C) \cup (B \cap C)$
   (g) $B \cap D$
   (h) $(B \cap D)^c$
   (i) $A - D$
   (j) $B - D$
   (k) $(A - D) \cup (B - D)$
   (l) $(A \cup B) - D$
9. let $P$, $Q$, $R$, and $S$, be subsets of a universal set $U$, Assume that $(P - Q) \subseteq (R \cap S)$.
   
   (a) Complete the following sentence:
   For each $x \in U$, if $x \in (P - Q)$, then ... .
   (b) Write a useful negation of the statement in Part (9a).
   (c) Write the contrapositive of the statement in Part (9a).
10. Let $U$ be the universal set. Consider the following statement:
    
    For all $A$, $B$, and $C$ that are subsets of $U$, if $A \subseteq B$, then $B^c \subseteq A^c$.
    
    (a) Identify three conditional statements in the given statement.
    (b) Write the contrapositive of this statement.
    (c) Write the negation of this statement.
11. Let $A$, $B$, and $C$ be subsets of some universal sets $U$. Draw a Venn diagram for each of the following situations.
    
    (a) $A \subseteq C$
    (b) $A \cap B = \emptyset$
    (c) $A \not\subseteq B$, $B \not\subseteq A$, $C \subseteq A$, and $C \not\subseteq B$
    (d) $A \subseteq B$, $C \subseteq B$, and $A \cap C = \emptyset$
12. Let $A$, $B$, and $C$ be subsets of some universal sets $U$. For each of the following, draw a general Venn diagram for the three sets and then shade the indicated region.
    
    (a) $A \cap B$
    (b) $A \cap C$
    (c) $(A \cap B) \cup (A \cap C)$
    (d) $B \cup C$
    (e) $A \cap (B \cup C)$
    (f) $(A \cap B) - C$
13. We can extend the idea of consecutive integers (See Exercise (2) in Section 3.5) to represent four consecutive integers as $m$, $m + 1$, $m + 2$, and $m + 3$, where $m$ is an integer. There are other ways to represent four consecutive integers. For example, if $k \in \mathbb{Z}$, then $k - 1$, $k$, $k + 1$, and $k + 2$ are four consecutive integers.
    
    (a) Prove that for each $n \in \mathbb{Z}$, $n$ is the sum of four consecutive integers if and only if $n \equiv 2$ (mod 4).
    (b) Use set builder notation or the roster method to specify the set of integers that are the sum of four consecutive integers.
    (c) Specify the set of all natural numbers that can be written as the sum of four consecutive natural numbers.
    (d) Prove that for each $n \in \mathbb{Z}$, $n$ is the sum of eight consecutive integers if and only if $n \equiv 4$ (mod 8).
    (e) Use set builder notation or the roster method to specify the set of integers that are the sum of eight consecutive integers.
    (f) Specify the set of all natural numbers can be written as the sum of eight consecutive natural numbers.
14. One of the properties of real numbers is the so-called Law of Trichotomy, which states that if $a, b \in \mathbb{R}$, then exactly one of the following is true:

• $a < b$;
• $a = b$;
• $a > b$.
  
  Is the following proposition concerning sets true or false? Either provide a proof that it is true or a counterexample showing it is false.
  
  If A and B are subsets of some universal set, then exactly one of the following is true:
• $A \subseteq B$;
• $A = B$;
• $B \subseteq A$.

Explorations and Activities

15. Intervals of Real Numbers. In previous mathematics courses, we have frequently used subsets of the real numbers called intervals. There are some common names and notations for intervals. These are given in the following table, where it is assumed that a and b are real numbers and $a < b$.

Interval Notation	Set Notation	Name
($a$, $b$) =	{$x \in \mathbb{R} \, | \, a < x < b$}	Open interval from $a$ to $b$
[$a$, $b$] =	{$x \in \mathbb{R} \, | \, a \le x \le b$}	Closed interval from $a$ to $b$
[$a$, $b$) =	{$x \in \mathbb{R} \, | \, a \le x < b$}	Half-open interval
($a$, $b$] =	{$x \in \mathbb{R} \, | \, a < x \le b$}	Half-open interval
($a$, $+ \infty$) =	{$x \in \mathbb{R} \, | \, x > a$}	Open ray
($- \infty$, $b$) =	{$x \in \mathbb{R} \, | \, x < b$}	Open ray
[$a$, $+ \infty$) =	{$x \in \mathbb{R} \, | \, x \ge a$}	Closed ray
($- \infty$, $b$] =	{$x \in \mathbb{R} \, | \, x \le b$}	Closed ray

(a) Is $(a, \, b)$ a proper subset of $(a, \, b]$? Explain.
(b) Is $[a, \, b]$ a subset of $(a, \,+ \infty)$? Explain.
(c) Use interval notation to describe

i. the intersection of the interval $[-3, \, 7]$ with the interval $(5, 9];$
ii. the union of the interval $[-3, 7]$ with the interval $(5, 9];$
iii. the set difference $[-3, 7] - (5, 9].$

(d) Write the set {$x \in \mathbb{R} \, | \, |x| \le 0.01$} using interval notation.
(e) Write the set {$x \in \mathbb{R} \, | \, |x| > 2$} as the union of two intervals.

16. More Work with Intervals. For this exercise, use the interval notation described in Exercise 15.

(a) Determine the intersection and union of $[2, 5]$ and $[-1, \, + \infty).$
(b) Determine the intersection and union of $[2, 5]$ and $[3.4, \, + \infty).$
(c) Determine the intersection and union of $[2, 5]$ and $[7, \, + \infty).$

Now let $a$, $b$ and $c$ be real numbers with $a < b$.

(d) Explain why the intersection of $[a, \, b]$ and $[c, \, + \infty)$ is either a closed interval, a set with one element, or the empty set.
(e)Explain why the union of $[a, \, b]$ and $[c, \,+ \infty)$ is either a closed ray or the union of a closed interval and a closed ray.

17. Proof of Theorem 5.5. To help with the proof by induction of Theorem 5.5, we first prove the following lemma. (The idea for the proof of this lemma was illustrated with the discussion of power set after the definition on page 222.)

Lemma 5.6

Let $A$ and $B$ be subsets of some universal set. If $A = B \cup \{x\}$, where $x \notin B$, then any subset of $A$ is either a subset of $B$ or a set of the form $C \cup \{x\}$, where $C$ is a subset of $B$.

Proof

Let $A$ and $B$ be subsets of some universal set, and assume that $A = B \cup \{x\}$ where $x \notin B$. Let $Y$ be a subset of $A$. We need to show that $Y$ is a subset of $B$ or that $Y = C \cup \{x\}$, where $C$ is some subset of $B$. There are two cases to consider: (1) $x$ is not an element of $Y$, and (2) $x$ is an element of $Y$.

Case 1: Assume that $x \notin Y$. Let $y \in Y$. Then. $y \in A$ and $y \ne x$. Since

$A = B \cup \{x\}$,

this means that $y$ must be in $B$. Therefore, $Y \subseteq B$.

Case 2: Assume that $x \in Y$. In this case, let $C = Y - \{x\}$. Then every element of $C$ is an element of $B$. Hence, we can conclude that $C \subseteq B$ and that $Y = C \cup \{x\}$.

Cases (1) and (2) show that if $Y \subseteq A$, then $Y \subseteq B$ or $Y = C \cup \{x\}$, where $C \subseteq B$.

To begin the induction proof of Theorem 5.5, for each nonnegative integer $n$, we let $P(n)$ be, “If a finite set has exactly $n$ elements, then that set has exactly $2^n$ subsets.”

(a) Verify that $P(0)$ is true. (This is the basis step for the induction proof.)
(b) Verify that $P(1)$ and $P(2)$ are true.
(c) Now assume that $k$ is a nonnegative integer and assume that $P(k)$ is true. That is, assume that if a set has $k$ elements, then that set has $2^k$ subsets. (This is the inductive assumption for the induction proof.) Let $T$ be a subset of the universal set with card$(T) = k + 1$, and let $x \in T$. Then the set $B = T - \{x\}$ has $k$ elements.

Now use the inductive assumption to determine how many subsets $B$ has. Then use Lemma 5.6 to prove that $T$ has twice as many subsets as $B$. This should help complete the inductive step for the induction proof.

Answer

Add texts here. Do not delete this text first.