7.3: Equivalence Classes
- Page ID
- 7077
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As was indicated in Section 7.2, an equivalence relation on a set \(A\) is a relation with a certain combination of properties (reflexive, symmetric, and transitive) that allow us to sort the elements of the set into certain classes. This is done by means of certain subsets of \(A\) that are associated with the elements of the set \(A\). This will be illustrated with the following example. Let \(A = \{a, b, c, d, e\}\), and let \(R\) be the relation on the set \(A\) defined as follows:
\(a\ R\ a\) \(b\ R\ b\) \(c\ R\ c\) \(d\ R\ d\) \(e\ R\ e\)
\(a\ R\ b\) \(b\ R\ a\) \(b\ R\ e\) \(e\ R\ b\)
\(a\ R\ e\) \(e\ R\ a\) \(c\ R\ d\) \(d\ R\ c\)
For each \(y \in A\), define the subset \(R[y]\) of \(A\) as follows:
\(R[y] = \{x \in A\ |\ x\ R\ y\}.\)
That is, \(R[y]\) consists of those elements in \(A\) such that \(x\ R\ y\). For example, using \(y = a\), we see that \(a\ R\ a\), \(b\ R\ a\), and \(e\ R\ a\), and so \(R[a] = \{a, b, e\}\).
- Determine \(R[b]\), \(R[c]\), \(R[d]\) and \(R[e]\).
- Draw a directed graph for the relation \(R\) and explain why \(R\) is an equivalence relation on \(A\).
- Which of the sets \(R[a]\), \(R[b]\), \(R[c]\), \(R[d]\) and \(R[e]\) are equal?
- Which of the sets \(R[a]\), \(R[b]\), \(R[c]\), \(R[d]\) and \(R[e]\) are disjoint?
As we will see in this section, the relationships between these sets is typical for an equivalence relation. The following example will show how different this can be for a relation that is not an equivalence relation.
Let \(A = \{a, b, c, d\}\), and let \(S\) be the relation on the set \(A\) defined as follows:
\(b\ S\ b\) \(c\ S\ c\) \(d\ S\ d\) \(e\ S\ e\)
\(a\ S\ b\) \(a\ S\ d\) \(b\ S\ c\)
\(c\ S\ d\) \(d\ S\ c\)
5. Draw a digraph that represents the relation \(S\) on \(A\). Explain why \(S\) is not an equivalence relation on \(A\).
For each \(y \in A\), define the subset \(S[y]\) of \(A\) as follows:
\(S[y] = \{x \in A\ |\ x\ S\ y\} = \{x \in A\ |\ (x, y) \in S\}.\)
For example, using \(y = b\), we see that \(S[b] = \{a, b\}\) since \((a, b) \in S\) and \((b, b) \in S\). In addition, we see that \(S[a] = \emptyset\) since there is no x 2 A such that.x;a/ 2 S.
6. Determine \(S[c]\), \(S[d]\), and \(S[e]\).
7. Which of the sets \(S[a]\), \(S[b]\), \(S[c]\), \(S[d]\), and \(S[e]\) are equal?
8. Which of the sets \(S[b]\), \(S[c]\), \(S[d]\), and \(S[e]\) are disjoint?
An important equivalence relation that we have studied is congruence modulo \(n\) on the integers. We can also define subsets of the integers based on congruence modulo \(n\). We will illustrate this with congruence modulo 3. For example, we can define \(C[0]\) to be the set of all integers a that are congruent to 0 modulo 3. That is,
\(C[0] = \{a \in \mathbb{Z}\ |\ a \equiv 0\text{ (mod 3)}\}.\)
Since an integer \(a\) is congruent to 0 modulo 3 if an only if 3 divides \(a\), we can use the roster method to specify this set as follows:
\(C[0] = \{..., -9, -6, -3, 0, 3, 6, 9, ...\}.\)
- Use the roster method to specify each of the following sets:
(a) The set \(C[1]\) of all integers \(a\) that are congruent to 1 modulo 3. That is, \(C[1] = \{a \in \mathbb{Z}\ |\ a \equiv 1 \text{ (mod 3)}\}.\)
(b) The set \(C[2]\) of all integers \(a\) that are congruent to 2 modulo 3. That is, \(C[2] = \{a \in \mathbb{Z}\ |\ a \equiv 2 \text{ (mod 3)}\}.\)
(c) The set \(C[3]\) of all integers \(a\) that are congruent to 3 modulo 3. That is, \(C[3] = \{a \in \mathbb{Z}\ |\ a \equiv 3 \text{ (mod 3)}\}.\) - Now consider the three sets, \(C[0]\), \(C[1]\), and \(C[2]\).
(a) Determine the intersection of any two of these sets. That is, determine \(C[0] \cap C[1]\), \(C[0] \cap C[2]\), and \(C[1] \cap C[2]\).
(b) Let \(n = 734\). What is the remainder when \(n\) is divided by 3? Which of the three sets, if any, contains \(n = 734\)?
(c) Repeat Part (2b) for \(n = 79\) and for \(n = -79\).
(d) Do you think that \(C[0] \cup C[1] \cup C[2] = \mathbb{Z}\) Explain.
(e) Is the set \(C[3]\) equal to one of the sets \(C[0]\), \(C[1]\), or \(C[2]\)?
(f) We can also define \(C[4] = \{a \in \mathbb{Z}\ |\ a \equiv 4 \text{ (mod 3)}\}\). Is this set equal to any of the previous sets we have studied in this part? Explain.
The Definition of an Equivalence Class
We have indicated that an equivalence relation on a set is a relation with a certain combination of properties (reflexive, symmetric, and transitive) that allow us to sort the elements of the set into certain classes. We saw this happen in the preview activities. We can now illustrate specifically what this means. For example, in Preview Activity \(\PageIndex{2}\), we used the equivalence relation of congruence modulo 3 on \(\mathbb{Z}\) to construct the following three sets:
\[\begin{array} {rcl} {C[0]} &= & {\{a \in \mathbb{Z}\ |\ a \equiv 0\text{ (mod 3)}\},} \\ {C[1]} &= & {\{a \in \mathbb{Z}\ |\ a \equiv 1\text{ (mod 3)}\},\text{ and}} \\ {C[2]} &= & {\{a \in \mathbb{Z}\ |\ a \equiv 2\text{ (mod 3)}\}.} \end{array}\]
The main results that we want to use now are Theorem 3.31 and Corollary 3.32 on page 150. This corollary tells us that for any \(a \in \mathbb{Z}\), \(a\) is congruent to precisely one of the integers 0, 1, or 2. Consequently, the integer \(a\) must be congruent to 0, 1, or 2, and it cannot be congruent to two of these numbers. Thus
- For each \(a \in \mathbb{Z}\), \(a \in C[0]\), \(a \in C[1]\), or \(a \in C[2]\); and
- \(C[0] \cap C[1] = \emptyset\), \(C[0] \cap C[2] = \emptyset\), and \(C[1] \cap C[2] = \emptyset\).
This means that the relation of congruence modulo 3 sorts the integers into three distinct sets, or classes, and that each pair of these sets have no elements in common. So if we use a rectangle to represent \(\mathbb{Z}\), we can divide that rectangle into three smaller rectangles, corresponding to \(C[0]\), \(C[1]\), and \(C[2]\) and we might picture this situation as follows:
The Integers
| \(C[0]\) consisting of all integers with a remainder of 0 when divided by 3 | \(C[1]\) consisting of all integers with a remainder of 1 when divided by 3 | \(C[2]\) consisting of all integers with a remainder of 2 when divided by 3 |
Each integer is in exactly one of the three sets (C[0]\), \(C[1]\), or \(C[2]\), and two integers are congruent modulo 3 if and only if they are in the same set. We will see that, in a similar manner, if \(n\) is any natural number, then the relation of congruence modulo \(n\) can be used to sort the integers into \(n\) classes. We will also see that in general, if we have an equivalence relation \(R\) on a set \(A\), we can sort the elements of the set \(A\) into classes in a similar manner.
Let \(\sim\) be an equivalence relation on a nonempty set \(A\). For each \(a \in A\), the equivalence class of \(a\) determined by \(\sim\) is the subset of \(A\), denoted by [\(a\)], consisting of all the elements of \(A\) that are equivalent to \(a\). That is,
\([a] = \{x \in A\ |\ x \sim a\}.\)
We read [\(a\)] as "the equivalence class of \(a\)" or as "bracket \(a\)."
Notes
- We use the notation [\(a\)] when only one equivalence relation is being used. If there is more than one equivalence relation, then we need to distinguish between the equivalence classes for each relation. We often use something like \([a]_{\sim}\), or if \(R\) is the name of the relation, we can use \(R[a]\) or \([a]_R\) for the equivalence class of a determined by \(R\). In any case, always remember that when we are working with any equivalence relation on a set A if \(a \in A\), then the equivalence class [\(a\)] is a subset of \(A\).
- We know that each integer has an equivalence class for the equivalence relation of congruence modulo 3. But as we have seen, there are really only three distinct equivalence classes. Using the notation from the definition, they are:
\([0] = \{a \in \mathbb{Z}\ |\ a \equiv 0 \text{ (mod 3)}\},\)
\([1] = \{a \in \mathbb{Z}\ |\ a \equiv 1 \text{ (mod 3)}\},\) and
\([2] = \{a \in \mathbb{Z}\ |\ a \equiv 2 \text{ (mod 3)}\}.\)
Without using the terminology at that time, we actually determined the equivalence classes of the equivalence relation \(R\) in Preview Activity \(\PageIndex{1}\). What are the distinct equivalence classes for this equivalence relation?
- Answer
-
Add texts here. Do not delete this text first.
Congruence Modulo \(n\) and Congruence Classes
In Preview Activity \(\PageIndex{2}\), we used the notation \(C[k]\) for the set of all integers that are congruent to \(k\) modulo 3. We could have used a similar notation for equivalence classes, and this would have been perfectly acceptable. However, the notation [\(a\)] is probably the most common notation for the equivalence class of \(a\). We will now use this same notation when dealing with congruence modulo \(n\) when only one congruence relation is under consideration.
Let \(n \in \mathbb{N}\). Congruence modulo \(n\) is an equivalence relation on \(\mathbb{Z}\). So for \(a \in \mathbb{Z}\),
\([a] = \{x \in \mathbb{Z}\ |\ x \equiv a \text{ (mod \(n\))}\}.\)
In this case, [\(a\)] is called the congruence class of \(a\) modulo \(n\).
We have seen that congruence modulo 3 divides the integers into three distinct congruence classes. Each congruence class consists of those integers with the same remainder when divided by 3. In a similar manner, if we use congruence modulo 2, we simply divide the integers into two classes. One class will consist of all the integers that have a remainder of 0 when divided by 2, and the other class will consist of all the integers that have a remainder of 1 when divided by 2. That is, congruence modulo 2 simply divides the integers into the even and odd integers.
Determine all of the distinct congruence classes for the equivalence relation of congruence modulo 4 on the integers. Specify each congruence class using the roster method.
- Answer
-
Add texts here. Do not delete this text first.
Properties of Equivalence Classes
As we have seen, in Preview Activity \(\PageIndex{1}\), the relation R was an equivalence relation. For that preview activity, we used \(R[y]\) to denote the equivalence class of \(y \in A\), and we observed that these equivalence classes were either equal or disjoint.
However, in Preview Activity \(\PageIndex{1}\), the relation \(S\) was not an equivalence relation, and hence we do not use the term “equivalence class” for this relation. We should note, however, that the sets \(S[y]\) were not equal and were not disjoint. This exhibits one of the main distinctions between equivalence relations and relations that are not equivalence relations.
In Theorem 7.14, we will prove that if \(\sim\) is an equivalence relation on the set \(A\), then we can “sort” the elements of \(A\) into distinct equivalence classes. The properties of equivalence classes that we will prove are as follows: (1) Every element of A is in its own equivalence class; (2) two elements are equivalent if and only if their equivalence classes are equal; and (3) two equivalence classes are either identical or they are disjoint.
Let \(A\) be a nonempty set and let \(\sim\) be an equivalence relation on the set \(A\). Then,
- For each \(a \in A\), \(a \in [a]\).
- For each \(a, b \in A\), \(a \sim b\) if and only if \([a] = [b]\),
- For each \(a, b \in A\), \([a] = [b]\) or \([a] \cap [b] = \emptyset\).
- Proof
-
Let A be a nonempty set and assume that \(\sim\) is an equivalence relation on \(A\). To prove the first part of the theorem, let \(a \in A\). Since \(\sim\) is an equivalence relation on \(A\), it is reflexive on \(A\). Thus, \(a \sim a\), and we can conclude that \(a \in [a]\).
The second part of this theorem is a biconditional statement. We will prove it by proving two conditional statements. We will first prove that if \(a \sim b\), then \([a] = [b]\). So let \(a, b \in A\) and assume that \(a \sim b\). We will now prove that the two sets \([a]\) and \([b]\) are equal. We will do this by proving that each is a subset of the other.
First, assume that \(x \in [a]\). Then, by definition, \(x \sim a\). Since we have assumed that \(a \sim b\), we can use the transitive property of \(\sim\) to conclude that \(x \sim b\), and this means that \(x \in [b]\). This proves that \([a] \subseteq [b]\).
We now assume that \(y \in [b]\). This means that \(y \sim b\), and hence by the symmetric property, that \(b \sim y\). Again, we are assuming that \(a \sim b\). So we have
\(a \sim b\) and \(b \sim y\).
We use the transitive property to conclude that \(a \sim y\) and then, using the symmetric property, we conclude that \(y \sim a\). This proves that \(y \in [a]\) and, hence, that \([b] \subseteq [a]\). This means that we can conclude that if \(a \sim b\), then \([a] = [b]\).
We must now prove that if \([a] = [b]\), then \(a \sim b\). Let \(a, b \in A\) and assume that \([a] = [b]\). Using the first part of the theorem, we know that \(a \in [a]\) and since the two sets are equal, this tells us that \(a \in [b]\). Hence by the definition of \([b]\), we conclude that \(a \sim b\). This completes the proof of the second part of the theorem.
For the third part of the theorem, let \(a, b \in A\). Since this part of the theorem is a disjunction, we will consider two cases: Either
\([a] \cap [b] = \emptyset\) or \([a] \cap [b] \ne \emptyset\).
In the case where \([a] \cap [b] = \emptyset\), the first part of the disjunction is true, and hence there is nothing to prove. So we assume that \([a] \cap [b] \ne \emptyset\); and will show that \([a] = [b]\). Since \([a] \cap [b] \ne \emptyset\), there is an element \(x\) in \(A\) such that
\(a \in [a] \cap [b]\).
This means that \(x \in [a]\) and \(x \in [b]\). Consequently, \(x \in a\) and \(x \in b\), and so we can use the first part of the theorem to conclude that \([x] = [a]\) and \([x] = [b]\). Hence, \([a] = [b]\), and we have proven that \([a] = [b]\) or \([a] \cap [b] = \emptyset\).
Theorem 7.14 gives the primary properties of equivalence classes. Consequences of these properties will be explored in the exercises. The following table restates the properties in Theorem 7.14 and gives a verbal description of each one.
| Formal Statement from Theorem 7.14 | Verbal Description |
|---|---|
| For each \(a \in A\), \(a \in [a]\). | Every element of \(A\) is in its own equivalence class. |
| For each \(a, b \in A\), \(a \sim b\) if and only if \([a] = [b]\). | Two elements of \(A\) are equivalent if and only if their equivalence classes are equal. |
| For each \(a, b \in A\), \([a] = [b]\) or \([a] \cap [b] = \emptyset\) | Any two equivalence classes are either equal or they are disjoint. This means that if two equivalence classes are not disjoint then they must be equal. |
Let \(f: \mathbb{R} \to \mathbb{R}\) be defined by \(f(x) = x^2 - 4\) for each \(x \in \mathbb{R}\). Define a relation \(\sim\) on \(\mathbb{R}\) as follows:
For \(a, b \in \mathbb{R}\), \(a \sim b\) if and only if \(f(a) = f(b)\).
In Exercise (6) of Section 7.2, we proved that \(\sim\) is an equivalence relation on \(\mathbb{R}\). Consequently, each real number has an equivalence class. For this equivalence relation,
- Determine the equivalence classes of 5, -5, 10, -10, \(\pi\), and \(-\pi\).
- Determine the equivalence class of 0.
- If \(a \in \mathbb{R}\), use the roster method to specify the elements of the equivalence class \([a]\).
- Answer
-
Add texts here. Do not delete this text first.
The results of Theorem 7.14 are consistent with all the equivalence relations studied in the preview activities and in the progress checks. Since this theorem applies to all equivalence relations, it applies to the relation of congruence modulo \(n\) on the integers. Because of the importance of this equivalence relation, these results for congruence modulo n are given in the following corollary.
Let \(n \in \mathbb{N}\). For each \(a \in \mathbb{Z}\), let \([a]\) represent the congruence class of \(a\) modulo \(n\).
- For each \(a \in \mathbb{Z}\), \(a \in [a]\).
- For each \(a, b \in \mathbb{Z}\), \(a \equiv b\) (mod \(n\)) if and only if \([a] = [b]\).
- For each \(a, b \in \mathbb{Z}\), \([a] = [b]\) or \([a] \cap [b] = \emptyset\).
For the equivalence relation of congruence modulo \(n\), Theorem 3.31 and Corollary 3.32 tell us that each integer is congruent to its remainder when divided by \(n\), and that each integer is congruent modulo \(n\) to precisely one of one of the integers \(0, 1, 2, ..., n - 1\). This means that each integer is in precisely one of the congruence classes \([0], [1], [2], ..., [n - 1]\). Hence, Corollary 7.16 gives us the following result
Let \(n \in \mathbb{N}\). For each \(a \in \mathbb{Z}\), let \([a]\) represent the congruence class of \(a\) modulo \(n\).
- \(\mathbb{Z} = [0] \cup [1] \cup [2] \cup \cdot\cdot\cdot \cup [n - 1]\)
- For \(j, k \in \{0, 1, 2, ..., n -1\}\), if \(j \ne k\), then \([j] \cap [k] = \emptyset\).
Partitions and Equivalence Relations
A partition of a set \(A\) is a collection of subsets of \(A\) that “breaks up” the set \(A\) into disjoint subsets. Technically, each pair of distinct subsets in the collection must be disjoint. We then say that the collection of subsets is pairwise disjoint. We introduce the following formal definition.
Let \(A\) be a nonempty set, and let \(\mathcal{C}\) be a collection of subsets of \(A\). The collection of subsets \(\mathcal{C}\) is a partition of \(A\) provided that
- For each \(V \in \mathcal{C}\), \(V \ne \emptyset\).
- For each \(x \in A\), there exists a \(V \in \mathcal{C}\) such that \(x \in V\).
- For every \(V, W \in \mathcal{C}\), \(V = W\) or \(V \cap W = \emptyset\).
There is a close relation between partitions and equivalence classes since the equivalence classes of an equivalence relation form a partition of the underlying set, as will be proven in Theorem 7.18. The proof of this theorem relies on the results in Theorem 7.14.
Let \(\sim\) be an equivalence relation on the nonempty set \(A\). Then the collection \(\mathcal{C}\) of all equivalence classes determined by \(\sim\) is a partition of the set \(A\).
- Proof
-
Let \(\sim\) be an equivalence relation on the nonempty set \(A\), and let \(\mathcal{C}\) be the collection of all equivalence classes determined by \(\sim\). That is,
\(\mathcal{C} = \{[a]\ |\ a \in A\}\).
We will use Theorem 7.14 to prove that \(\mathcal{C}\) is a partition of \(A\).
Part (1) of Theorem 7.14 states that for each \(a \in A\), \(a \in [a]\). In terms of the equivalence classes, this means that each equivalence class is nonempty since each element of \(A\) is in its own equivalence class. Consequently, \(\mathcal{C}\), the collection of all equivalence classes determined by \(\sim\), satisfies the first two conditions of the definition of a partition.
We must now show that the collection \(\mathcal{C}\) of all equivalence classes determined by \(\sim\) satisfies the third condition for being a partition. That is, we need to show that any two equivalence classes are either equal or are disjoint. However, this is exactly the result in Part (3) of Theorem 7.14.
Hence, we have proven that the collection C of all equivalence classes determined by \(\sim\) is a partition of the set A.
Note: Theorem 7.18 has shown us that if \(\sim\) is an equivalence relation on a nonempty set \(A\), then the collection of the equivalence classes determined by \(\sim\) form a partition of the set \(A\).
This process can be reversed. This means that given a partition \(\mathcal{C}\) of a nonempty set \(A\), we can define an equivalence relation on \(A\) whose equivalence classes are precisely the subsets of \(A\) that form the partition. This will be explored in Exercise (12).
- Let \(A = \{a, b, c, d, e\}\) and let \(\sim\) be the relation on \(A\) that is represented by the directed graph in Figure 7.4.
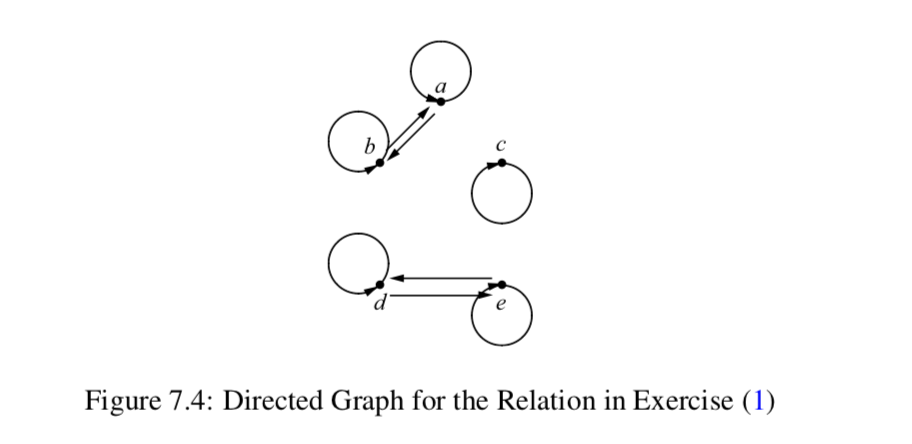
Prove that \(\sim\) is an equivalence relation on the set \(A\), and determine all of the equivalence classes determined by this equivalence relation. - Let \(A = \{a, b, c, d, e, f\}\), and assume that \(\sim\) is an equivalence relation on \(A\). Also assume that it is known that
\(a \sim b\) \(a \nsim c\) \(e \sim f\)
\(a \sim d\) \(a \nsim f\) \(e \nsim c\)
Draw a complete directed graph for the equivalence relation \(\sim\) on the set \(A\), and then determine all of the equivalence classes for this equivalence relation. - Let \(A = \{0, 1, 2, 3, ..., 999, 1000\}\). Define the relation \(R\) on \(A\) as follws:
For \(x, y \in A\), \(x\ R\ y\) if and only if \(x\) and \(y\) have the same number of digits.Prove that \(R\) is an equivalence relation on the set \(A\) and determine all of the distinct equivalence classes determined by \(R\).
- Determine all of the congruence classes for the relation of congruence modulo 5 on the set of integers.
- Let \(\mathbb{Z}_9 = \{0, 1, 2, 3, 4, 5, 6, 7, 8\}\).
(a) Define the relation \(\sim\) on \(\mathbb{Z}_9\) as follows: for all \(a, b \in \mathbb{Z}_9\), \(a \sim b\) if and only if \(a^2 \equiv b^2\) (mod 9). Prove that \(\sim\) is an equivalence relation on \(\mathbb{Z}_9\) and determine all of the distinct equivalence classes of this equivalence relation.
(b) Define the relation \(\approx\) on \(\mathbb{Z}_9\) as follows: For all \(a, b \in \mathbb{Z}_9\), \(a \approx b\) if and only if \(a^3 \equiv b^3\) (mod 9). Prove that \(\approx\) is an equivalence relation on \(\mathbb{Z}_9\) and determine all of the distinct equivalence classes of this equivalence relation. - Define the relation \(\sim\) on \(\mathbb{Q}\) as follows: For \(a, b \in \mathbb{Q}\), \(a \sim b\) if and only if \(a - b \in \mathbb{Z}\). In Progress Check 7.9 of Section 7.2, we showed that the relation \(\sim\) is an equivalence relation on \(\mathbb{Q}\). Also, see Exercise (9) in Section 7.2.
(a) Prove that \([\dfrac{5}{7} = \{m + \dfrac{5}{7}\ |\ m \in \mathbb{Z}\}\).
(b) If \(a \in \mathbb{Z}\), then what is the equivalence class of \(a\)?
(c) If \(a \in \mathbb{Z}\), prove that there is a bijection from \([a]\) to \([\dfrac{5}{7}]\). - Define the relation \(\sim\) on \(\mathbb{R}\) as follows:
For \(x, y \in \mathbb{R}\), \(x \sim y\) if and only if \(x - y \in \mathbb{Q}\).
(a) Prove that \(\sim\) is an equivalence relation on \(\mathbb{R}\).
(b) List four different real numbers that are in the equivalence class of \(\sqrt{2}\).
(c) If \(a \in \mathbb{Q}\), what is the equivalence class of \(a\)?
(d) Prove that \([\sqrt{2}] = \{r + \sqrt{2}\ |\ r \in \mathbb{Q}\}\).
(e) If \(a \in \mathbb{Q}\), prove that there is a bijection from \([a]\) to \([\sqrt{2}]\). - Define the relation \(\sim\) on \(\mathbb{Z}\) as follows: For \(a, b \in \mathbb{Z}\), \(a \sim b\) if and only if \((2a + 3b \equiv 0\) (mod 5). The relation \(\sim\) is an equivalence relation on \(\mathbb{Z}\). (See Exercise (13) in Section 7.2). Determine all the distinct equivalence classes for this equivalence relation.
- Let \(A = \mathbb{Z} \times (\mathbb{Z} - \{0\})\). That is, \(A = \{(a, b) \in \mathbb{Z} \times \mathbb{Z}\ |\ b \ne 0\}\). Define the relation \(\approx\) on \(A\) as follows:
For \((a, b), (c, d) \in A\), \((a, b) \approx (c, d)\) if and only if \(ad = bc\).
(a) Prove that \(\approx\) is an equivalence relation on \(A\).
(b) Why was it necessary to include the restriction that \(b \ne 0\) in the definition of the set \(A\)?
(c) Determine an equation that gives a relation between \(a\) and \(b\) if \((a, b) \in A\) and \((a, b) \approx (2, 3)\).
(d) Determine at least four different elements in [(2, 3)], the equivalence class of (2, 3).
(e) Use set builder notion to describe [(2, 3)], the equivalence class of (2, 3). - For \((a, b) (c, d) \in \mathbb{R} \times \mathbb{R}\), define \((a, b) \sim (c, d)\) if and only if \(a^2 + b^2 = c^2 + d^2\). In Exercise (15) of Section 7.2, we proved that \(\sim\) is an equivalence relation on \(\mathbb{R} \times \mathbb{R}\).
(a) Determine the equivalence class of (0, 0).
(b) Use set builder notation (and do not use the symbol \(\sim\)) to describe the equivalence class of (2, 3) and then give a geometric description of this equivalence class.
(c) Give a geometric description of a typical equivalence class for this equivalence relation.
(d) Let \(\mathbb{R}^{\ast} = \{x \in \mathbb{R}\ |\ x \ge 0\}\). Prove that there is a one-to-one correspondence (bijection) between \(\mathbb{R}^{\ast}\) and the set of all equivalence classes for this equivalence relation. - Let \(A\) be a nonempty set and let \(\sim\) be an equivalence relation on \(A\). Prove each of the following:
(a) For each \(a, b \in A\), \(a \nsim b\) if and only if \([a] \cap [b] = \emptyset\).
(b) For each \(a, b \in A\), if \([a] \ne [b]\), then \([a] \cap [b] = \emptyset\).
(c) For each \(a, b \in A\), if \([a] \cap [b] \ne \emptyset\) then \([a] = [b]\).
Explorations and Activities - A Partition Defines an Equivalence Relation. Let \(A = \{a, b, c, d, e\}\) and let \(\mathcal{C} = \{\{a, b, c\}, \{d, e\}\}\).
(a) Explain why \(\mathcal{C}\) is a partition of \(A\).
Define a relation \(\sim\) on \(A\) as follows: For \(x, y \in A\), \(x \sim y\) if and only if there exists a set \(U\) in \(\mathcal{C}\) such that \(x \in U\) and \(y \in U\).
(b) Prove that \(\sim\) is an equivalence relation on the set \(A\), and then determine all the equivalence classes for \(\sim\). How does the collection of all equivalence classes compare to \(\mathcal{C}\)?
What we did for the specific partition in Part (12b) can be done for any partition of a set. So to generalize Part (12b), we let \(A\) be a nonempty set and let \(\mathcal{C}\) be a partition of \(A\). We then define a relation \(\sim\) on \(A\) as follows:
For \(x, y \in A\), \(x \sim y\) if and only if there exists a set \(U\) in \(\mathcal{C}\) such that \(x \in U\) and \(y \in U\).
(c) Prove that \(\sim\) is an equivalence relation on the set \(A\).
(d) Let \(a \in A\) and let \(U \in \mathcal{C}\) such that \(a \in U\). Prove that \([a] = U\). - Equivalence Relations on a Set of Matrices. The following exercises require a knowledge of elementary linear algebra. We let \(\mathcal{M}_{n,n} (\mathbb{R}\) be the set of all \(n\) by \(n\) matrices with real number entries.
(a) Define a relation \(\sim\) on \(\mathcal{M}_{n,n} (\mathbb{R}\) as follows: For all \(A, B \in \mathcal{M}_{n,n} (\mathbb{R}\), \(A \sim B\) if and only if there exists an invertible matrix \(P\) in \(\mathcal{M}_{n,n} (\mathbb{R}\) such that \(B = PAP^{-1}\). Is \(\sim\) an equivalence relation on \(\mathcal{M}_{n,n} (\mathbb{R}\)? Justify your conclusion.
(b) Define a relation \(R\) on \(\mathcal{M}_{n,n} (\mathbb{R}\) as follows: For all \(A, B \in \mathcal{M}_{n,n} (\mathbb{R}\), \(A\ R\ B\) if and only if det(\(A\)) = det(\(B\)). Is \(R\) an equivalence relation on \(\mathcal{M}_{n,n} (\mathbb{R}\)? Justify your conclusion.
(c) Let \(\sim\) be an equivalence relation on \(\mathbb{R}\). Define a relation \(\approx\) on \(\mathcal{M}_{n,n} (\mathbb{R}\) as follow: For all \(A, B \in \mathcal{M}_{n,n} (\mathbb{R}\), \(A \approx B\) if and only if det(\(A\)) \(\sim\) det(\(B\)). Is \(\approx\) an equivalence relation on \(\mathcal{M}_{n,n} (\mathbb{R}\)? Justify your conclusion.
- Answer
-
Add texts here. Do not delete this text first.


