1.3: Topic C- Place Value

Topic C: Place Value

As you know, we count much higher than ten in our world. Each place in a number has a value.

The ones place tells how many ones there are.

• 3 means 3 ones. \(\square \square \square\)
• 0 means 0 ones
• 9 means 9 ones \(\square \square \square \square \\ \square \square \square \square \square\)

9 is the largest amount that we can express (write or say) with one digit.

The tens place shows how many tens there are. The ones place must have a digit in it before there can be a digit in the tens place.

Every ten is ten ones.

43 means 4 tens and 3 ones.

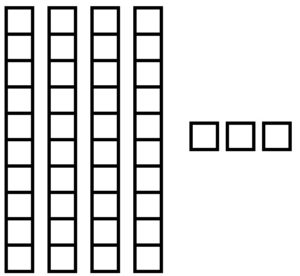
20 means 2 tens and 0 ones. The zero holds the ones place.

99 means 9 tens and 9 ones. 99 is the largest amount that we can express (write or say) using only two digits.

Exercise 1

Fill in the blanks to make each sentence true. Draw a picture for questions c, f, h, and j like the examples. Check your work using the answer key at the end of the exercise. Ask your instructor to check your sketches.

Example

49 means 4 tens and 9 ones.

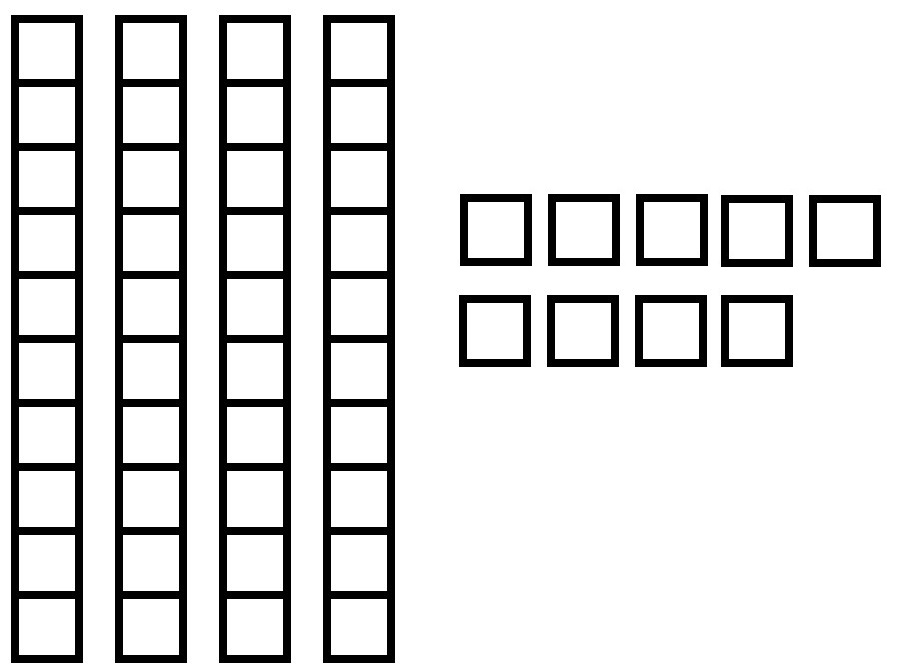
1. 37 means _____ tens and _____ ones.
2. 65 means _____ tens and _____ ones.
3. 56 means _____ tens and _____ ones.
4. 87 means _____ tens and _____ ones
5. 33 means _____ tens and _____ ones.
6. 60 means _____ tens and _____ ones.

Answers to Exercise 1

1. 3 tens, 7 ones
2. 6 tens, 5 ones
3. 5 tens, 6 ones
4. 8 tens, 7 ones
5. 3 tens, 3 ones
6. 6 tens, 0 ones

The place to the left of the tens place is the hundreds place. It shows how many hundreds there are. A number written using three whole digits has a hundreds place, a tens place, and a ones place.

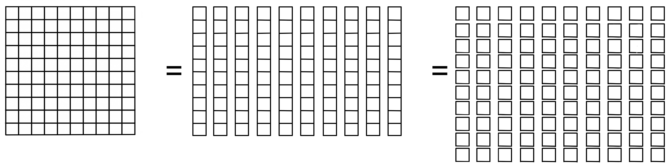
Every hundred is the same as ten tens, and every hundred is the same as one hundred ones.

Every hundred is ten tens – every hundred is the same as one hundred ones.

100 100 100

425 means 4 hundreds, 2 tens, and 5 ones

354 means 3 hundreds, 5 tens, and 4 ones

Exercise 2

Fill in the blanks to make each sentence true. Draw a picture for questions b, c, d, and e, like the examples. Check your work using the answer key at the end of the exercise. Ask your instructor to check your sketches.

1. 190 = 1 hundreds, 9 tens, 0 ones.
2. 555 = _____ hundreds, _____ tens, _____ ones.
3. 309 = _____ hundreds, _____ tens, _____ ones.
4. 499 = _____ hundreds, _____ tens, _____ ones.
5. 480 = _____ hundreds, _____ tens, _____ ones.

Answers to Exercise 2

2. 5 hundreds, 5 tines, 5 ones
3. 3 hundreds, 0 tens, 9 ones
4. 4 hundreds, 9 tens, 9 ones
5. 4 hundreds, 8 tens, 0 ones

Exercise 3

Count the hundreds, tens, and ones shown in the drawings. The pictures will help you understand the quantity of a number. Then write the numeral. The first one is done for you. Check your work using the answer key at the end of the exercise.

1. 2 hundreds, 0 tens, 3 ones = 203
   
   
2. hundreds, tens, ones =
   
3. hundreds, tens, ones =
   
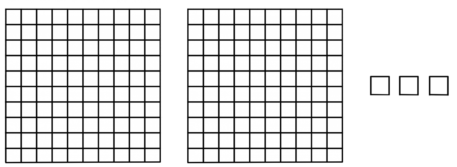
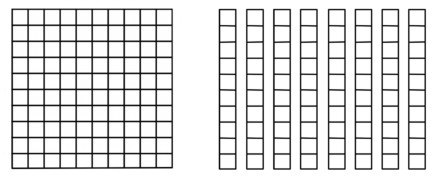
4. hundreds, tens, ones =
   

Answers to Exercise 3

2. 4 hundreds, 3 tens, 1 ones
3. 1 hundreds, 8 tens, 0 ones
4. 2 hundreds, 0 tens, 3 ones

Need more practice?

Ask your instructor for some fake money. Using the one, ten, and hundred dollar bills, practice trading ten of one type of bill for one of the next value.

Exercise 4

Write the place value name (ones, tens, hundreds) for each underlined digit. Check your work using the answer key at the end of the exercise.

1. 622 hundreds
2. 468 tens
3. 920
4. 920
5. 648
6. 426
7. 534
8. 555
9. 451
10. 901
11. 226
12. 486

Answers to Exercise 4

3. ones
4. hundreds
5. tens
6. ones
7. hundreds
8. tens
9. tens
10. ones
11. hundreds
12. ones

Exercise 5

Underline the digit for the place value named. Check your work using the answer key at the end of the exercise.

1. hundreds, 416
2. tens, 368
3. tens, 364
4. hundreds, 456
5. ones, 206
6. ones, 634

Answers to Exercise 5

1. 4
2. 6
3. 6
4. 4
5. 6
6. 4

Emotions Check

How are you feeling?

1. Are your palms moist?
2. How is your breathing?

Take control. Be the boss. If you are feeling anxious, practice your breathing exercise.

Remember: Breathe in slowly to the count of four, hold it for the count of four.

Reading and Writing Numerals

You know that the digits are 0 1 2 3 4 5 6 7 8 9 and that digits are arranged in different places so we can count larger amounts than our ten fingers!

When we use digits, we call what we write the numeral.

• 328 is a numeral
• 46 is a numeral
• 3 is a numeral

We use numerals to represent numbers.

If we think about language instead of mathematics it will be clearer.

Letters are used to make words. We respond to the meaning of words.

• Digits are the “letters” of math.
• Numerals are the “words” of math.
• Numbers are the “meaning” of math.

Now you know the place value of digits up to three places. Next you will learn to read and write numerals and number words. Some of the words to read and spell may be new to you.

The numerals from 1 to 12 have special words. These are:

Numerals 1 to 12

Numeral	Word Name
0	zero
1	one
2	two
3	three
4	four
5	five
6	six
7	seven
8	eight
9	nine
10	ten
11	eleven
12	twelve

The number names for numerals from 13 to 19 are made up of two parts. The first part tells us how many units. The second part (“teen”) tells us there is also 1 ten.

Numerals 13 to 19

Numeral	Word Name	Meaning
13	thirteen	three units and 1 ten
14	fourteen	four units and 1 ten
15	fifteen	five units and 1 ten
16	sixteen	six units and 1 ten
17	seventeen	seven units and 1 ten
18	eighteen	eight units and 1 ten
19	nineteen	nine units and 1 ten

Exercise 6

Write the word name for each number. Try not to look at the list. Check your work using the answer key at the end of the exercise.

1. 6
2. 17
3. 4
4. 14
5. 12
6. 13

Answers to Exercise 6

1. six
2. seventeen
3. four
4. fourteen
5. twelve
6. thirteen

The word names for the numbers 20 to 90 are also made up of two parts. The first part tells us how many groups of tens. The second part (“ty”) tells us we are counting groups of tens and not something else. The “-ty” may have come from a shortening of the word “ten”.

Numerals 20 to 90

Number	Word Name	Meaning
20	twenty	two tens
30	thirty	three tens
40	forty	four tens
50	fifty	five tens
60	sixty	six tens
70	seventy	seven tens
80	eighty	eight tens
90	ninety	nine tens

The names for the numbers between groups of tens also follow a pattern. The first number tells us how many tens. The second number tells us how many ones.

Numerals Between Tens

Tens Ones	Tens Ones	Tens Ones
20 twenty	30 thirty	40 forty
21 twenty-one	31 thirty-one	41 forty-one
22 twenty-two	32 thirty-two	42 forty-two
23 twenty-three	33 thirty-three	43 forty-three
24 twenty-four	34 thirty-four	44 forty-four
25 twenty-five	35 thirty-five	45 forty-five
26 twenty-six	36 thirty-six	46 forty-six
27 twenty-seven	37 thirty-seven	47 forty-seven
28 twenty-eight	38 thirty-eight	48 forty-eight
29 twenty-nine	39 thirty-nine	49 forty-nine

The written names for numbers that have tens and ones are written with a hyphen (-) between them. This pattern with the hyphen continues up to ninety-nine (99).

Exercise 7

Write the word names for these numbers. Check your work using the answer key at the end of the exercise.

1. 24 twenty-four
2. 35 thirty-five
3. 83 _____
4. 46 _____
5. 59 _____
6. 20 _____
7. 53 _____
8. 25 _____
9. 15 _____
10. 38 _____

Answers to Exercise 7

3. eighty-three
4. forty-six
5. fifty-nine
6. twenty
7. fifty-three
8. twenty-five
9. fifteen
10. thirty-eight

Exercise 8

Write the numerals for these word names. Check your work using the answer key at the end of the exercise.

1. ninety-nine 99
2. sixty-seven 67
3. eighty-one _____
4. eighteen _____
5. twenty-six _____
6. thirteen _____
7. thirty _____
8. forty-three _____

Answers to Exercise 8

3. 81
4. 18
5. 26
6. 13
7. 30
8. 43

When we write hundreds in words, we need two words. The first word tells us how many hundreds. The second word tells us we are counting hundreds.

200 two hundred

You now know how to write numbers in words up to 999.

Remember

• hyphen (-) between the tens and units
• no hyphen anywhere else
• no “s” on the hundred
• no “and” between the hundreds place and the tens place

\[\begin{array}{llll} \mathbf{367 } \text{ is made of:} & \mathbf{3} \text{ hundreds} & \mathbf{6} \text{ tens} & \mathbf{7} \text{ ones} \\ \text{Each is written:}& \text{three hundred} & \text{sixty} & \text{seven}\end{array} \\ \text{Put the parts together: } \textbf{three hundred sixty-seven}\]

Here is another example. Watch out for the empty space!

\[\begin{array}{llll} \mathbf{504 } \text{ is made of:} & \mathbf{5} \text{ hundreds} & \mathbf{0} \text{ tens} & \mathbf{4} \text{ ones} \\ \text{Each is written:}& \text{fice hundred} & & \text{four}\end{array} \\ \text{Put the parts together: } \textbf{five hundred four}\]

Here is another example. Watch out for the empty space!

\[\begin{array}{llll} \mathbf{890} \text{ is made of:} & \mathbf{8} \text{ hundreds} & \mathbf{9} \text{ tens} & \mathbf{0} \text{ ones} \\ \text{Each is written:}& \text{eight hundred} & \text{ninety} & \end{array} \\ \text{Put the parts together: } \textbf{eight hundred ninety}\]

Here is another example. Watch out for the empty space!

\[\begin{array}{llll} \mathbf{100} \text{ is made of:} & \mathbf{1} \text{ hundreds} & \mathbf{0} \text{ tens} & \mathbf{0} \text{ ones} \\ \text{Each is written:}& \text{one hundred} & & \end{array} \\ \text{Put the parts together: } \textbf{one hundred}\]

Remember

Empty spaces are not written in words.

Exercise 9

Write the word names for these numerals. Check your work using the answer key at the end of the exercise.

1. 623 is made of: _____
   Each is written: _____
   Put the parts together: _____
2. 364 is made of: _____
   Each is written: _____
   Put the parts together: _____
3. 213 is made of: _____
   Each is written: _____
   Put the parts together: _____
4. 405 is made of: _____
   Each is written: _____
   Put the parts together: _____

Now, write the word name for each number. Check your work using the answer key at the end of the exercise.

5. 704
6. 470
7. 993
8. 100
9. 972

Answers to Exercise 9

1. 623 is made of: 6 hundreds, 2 tens, 3 ones
   Each is written: six hundred, twenty, three
   Put the parts together: six hundred twenty-three
2. 364 is made of:3 hundreds, 6 tens, 4 ones
   Each is written: three hundred, sixty, four
   Put the parts together: three hundred sixty-four
3. 213 is made of: 2 hundreds. 1 ten, 3 ones
   Each is written: two hundred, thirteen
   Put the parts together: two hundred thirteen
4. 405 is made of:4 hundreds, 0 tens, 5 ones
   Each is written: four hundred, five
   Put the parts together: four hundred five
5. seven hundred four
6. four hundred seventy
7. nine hundred ninety-three
8. one hundred
9. nine hundred seventy-two

Topic C Self-Test

Mark /17 Aim 14/17

1. Write the place value for the underlined digit. (6 marks)
   1. 765
   2. 903
   3. 479
   4. 185
   5. 732
   6. 397
2. Write the word names for these numerals. (6 marks)
   1. 79
   2. 492
   3. 378
   4. 820
   5. 405
   6. 583
3. Write the numerals for these word names. (5 marks)
   1. five hundred forty-seven
   2. three hundred eighty
   3. two hundred seventy-five
   4. four hundred sixteen
   5. nine hundred twenty-three

Answers to Topic C Self-Test

1. 1. tens
   2. tens
   3. hundreds
   4. ones
   5. ones
   6. hundreds
2. 1. seventy-nine
   2. four hundred ninety-two
   3. three hundred seventy-eight
   4. eight hundred twenty
   5. four hundred five
   6. five hundred eighty-three
3. 1. 547
   2. 380
   3. 275
   4. 416
   5. 923