1.3: Multiplication and Division of Whole Numbers
- Page ID
- 22461
We begin this section by discussing multiplication of whole numbers. The first order of business is to introduce the various symbols used to indicate multiplication of two whole numbers.
Mathematical symbols that indicate multiplication
| Symbol | Example | |
|---|---|---|
| × | times symbol | 3 × 4 |
| · | dot | 3 · 4 |
| ( ) | parentheses | (3)(4) or 3(4) of (3)4 |
Products and Factors
In the expression \(3 · 4\), the whole numbers 3 and 4 are called the factors and \(3 · 4\) is called the product.
The key to understanding multiplication is held in the following statement.
Multiplication is equivalent to repeated addition.
Suppose, for example, that we would like to evaluate the product \(3 ·4\). Because multiplication is equivalent to repeated addition, \(3 · 4\) is equivalent to adding three fours. That is,
\[ 3 \cdot 4=\underbrace{4+4+4}_{\text { three fours }} \nonumber\]
Thus, \(3 · 4 = 12\). You can visualize the product \(3 · 4\) as the sum of three fours on a number line, as shown in Figure 1.6.

Like addition, the order of the factors does not matter.
\[ 4 \cdot 3=\underbrace{3+3+3+3}_{\text { four threes }} \nonumber\]
Thus, \(4 · 3 = 12\). Consider the visualization of \(4 · 3\) in Figure 1.7.

The evidence in Figure 1.6 and Figure 1.7 show us that multiplication is commutative. That is,
\[3 · 4=4 · 3 \nonumber\]
Commutative Property of Multiplication
If a and b are any whole numbers, then
\[a · b = b · a. \nonumber\]
The Multiplicative Identity
In Figure 1.8(a), note that five ones equals 5; that is, \(5 · 1 = 5\). On the other hand, in Figure 1.8(b), we see that one five equals five; that is, 1 · 5 = 5.
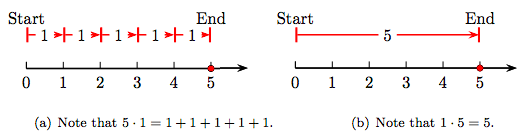
Because multiplying a whole number by 1 equals that identical number, the whole number 1 is called the multiplicative identity.
The Multiplicative Identity Property
If \(a\) is any whole number, then
a · 1 = a and 1 · a = a.
Multiplication by Zero
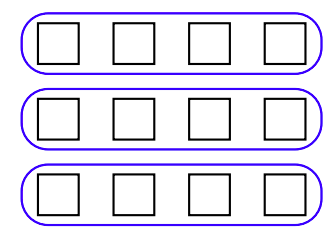
Because \(3 · 4 = 4 + 4 + 4\), we can say that the product \(3 · 4\) represents “3 sets of 4,” as depicted in Figure 1.9, where three groups of four boxes are each enveloped in an oval.
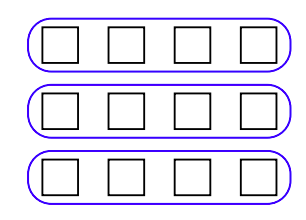
Therefore, \(0 · 4\) would mean zero sets of four. Of course, zero sets of four is zero.
Multiplication by Zero.
If a represents any whole number, then
\(a · 0 = 0\) and \(0 · a = 0\).
The Associative Property of Multiplication
Like addition, multiplication of whole numbers is associative. Indeed,
\[\begin{align*} 2 · (3 · 4) &= 2 · 12 \\[4pt] &= 24 \end{align*}\]
and
\[\begin{align*} (2 · 3) · 4 &=6 · 4 \\[4pt] &= 24. \end{align*}\]
The Associative Property of Multiplication.
If a, b, and c are any whole numbers, then
\[a · (b · c)=(a · b) · c. \nonumber\]
Multiplying Larger Whole Numbers
Much like addition and subtraction of large whole numbers, we will also need to multiply large whole numbers. Again, we hope the algorithm is familiar from previous coursework.
Example 1
Simplify: \(35 · 127\).
Solution
Align the numbers vertically. The order of multiplication does not matter, but we’ll put the larger of the two numbers on top of the smaller number. The first step is to multiply 5 times 127. Again, we proceed from right to left. So, 5 times 7 is 35. We write the 5, then carry the 3 to the tens column. Next, 5 times 2 is 10. Add the carry digit 3 to get 13. Write the 3 and carry the 1 to the hundreds column. Finally, 5 times 1 is 5. Add the carry digit to get 6.
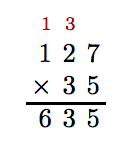
The next step is to multiply 3 times 127. However, because 3 is in the tens place, its value is 30, so we actually multiply 30 times 126. This is the same as multiplying 127 by 3 and placing a 0 at the end of the result.
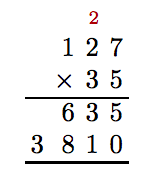
After adding the 0, 3 times 7 is 21. We write the 1 and carry the 2 above the 2 in the tens column. Then, 3 times 2 is 6. Add the carry digit 2 to get 8. Finally, 3 times 1 is 1.
All that is left to do is to add the results.
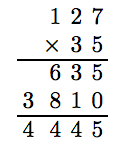
Thus, 35 · 127 = 4, 445.
Alternate Format
It does not hurt to omit the trailing zero in the second step of the multiplication, where we multiply 3 times 127. The result would look like this:
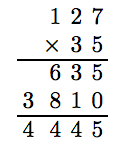
In this format, the zero is understood, so it is not necessary to have it physically present. The idea is that with each multiplication by a new digit, we indent the product one space from the right.
Exercise
Simplify: 56 · 335
- Answer
-
18,760
Division of Whole Numbers
We now turn to the topic of division of whole numbers. We first introduce the various symbols used to indicate division of whole numbers.
Mathematical Symbols that Indicate Division
| Symbol | Example | |
|---|---|---|
| ÷ | division symbol | 12 ÷ 4 |
| - | fraction bar | \(\frac{12}{4}\) |
| \(\longdiv{-}\) | division bar | \(4 \longdiv{12}\) |
Note that each of the following say the same thing; that is, “12 divided by 4 is 3.”
\(12 \div 4=3 \quad \text { or } \quad \frac{12}{4}=3 \quad \text { or } \quad 4 \sqrt{12}\)
Quotients, Dividends, and Divisors
In the statement
\(\frac{3}{4 ) 12}\)
the whole number 12 is called the dividend, the whole number 4 is called the divisor, and the whole number 3 is called the quotient. Note that this division bar notation is equivalent to
\(12 \div 4=3 \quad \text { and } \quad \frac{12}{4}=3.\)
The expression a/b means “a divided by b,” but this construct is also called a fraction.
Definition: Fraction
The expression
\( \frac{a}{b}\)
is called a fraction. The number \(a\) on top is called the numerator of the fraction; the number \(b\) on the bottom is called the denominator of the fraction.
The key to understanding division of whole numbers is contained in the following statement.
Division is equivalent to repeated subtraction.
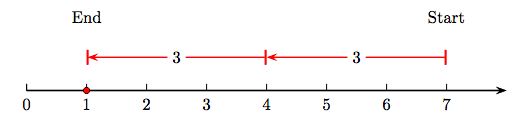
Suppose for example, that we would like to divide the whole number 12 by the whole number 4. This is equivalent to asking the question “how many fours can we subtract from 12?” This can be visualized in a number line diagram, such as the one in Figure 1.10.

In Figure 1.10, note that we if we subtract three fours from twelve, the result is zero. In symbols,
\( 12-\underbrace{4-4-4}_{\text { three fours }}=0.\)
Equivalently, we can also ask “How many groups of four are there in 12,” and arrange our work as shown in Figure 1.11, where we can see that in an array of twelve objects, we can circle three groups of four ; i.e., 12 ÷ 4 = 3.
In Figure 1.10 and Figure 1.11, note that the division (repeated subtraction) leaves no remainder. This is not always the case.
Example 2.
Divide 7 by 3.
Solution
In Figure 1.12, we can see that we can subtract two threes from seven, leaving a remainder of one.
Alternatively, in an array of seven objects, we can circle two groups of three, leaving a remainder of one.
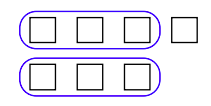
Both Figure 1.12 and Figure1.13 show that there are two groups of three in seven, with one left over. We say “Seven divided by three is two, with a remainder of one.
Exercise
Use both the number line approach and the array of boxes approach to divide 12 by 5.
Division is not Commutative
When dividing whole numbers, the order matters. For example
12 ÷ 4 = 3,
but 4 ÷ 12 is not even a whole number. Thus, if a and b are whole numbers, then a ÷ b does not have to be the same as b ÷ a.
Division is not Associative
When you divide three numbers, the order in which they are grouped will usually affect the answer. For example,
(48 ÷ 8) ÷ 2=6 ÷ 2
= 3,
but
48 ÷ (8 ÷ 2) = 48 ÷ 4
= 12.
Thus, if a, b, and c are whole numbers, (a ÷ b) ÷ c does not have to be the same as a ÷ (b ÷ c).
Division by Zero is Undefined
Suppose that we are asked to divide six by zero; that is, we are asked to calculate 6 ÷ 0. In Figure 1.14, we have an array of six objects.
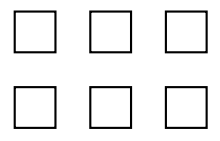
Now, to divide six by zero, we must answer the question “How many groups of zero can we circle in Figure 1.14?” Some thought will provide the answer: This is a meaningless request! It makes absolutely no sense to ask how many groups of zero can be circled in the array of six objects in Figure 1.14.
Division by Zero
Division by zero is undefined. Each of the expressions
\(6 \div 0 \quad \text { and } \quad \frac{6}{0} \quad \text { and } \quad 0 ) \overline{6}\)
is undefined.
On the other hand, it make sense to ask “What is zero divided by six?” If we create an array of zero objects, then ask how many groups of six we can circle, the answer is “zero groups of six.” That is, zero divided by six is zero.
\( 0 \div 6=0 \quad \text { and } \quad \frac{0}{6}=0 \quad \text { and } \quad 6 \frac{0}{0}\)
Dividing Larger Whole Numbers
We’ll now provide a quick review of division of larger whole numbers, using an algorithm that is commonly called long division. This is not meant to be a thorough discussion, but a cursory one. We’re counting on the fact that our readers have encountered this algorithm in previous courses and are familiar with the process.
Example 3
Simplify: 575/23.
Solution
We begin by estimating how many times 23 will divide into 57, guessing 1. We put the 1 in the quotient above the 7, multiply 1 times 23, place the answer underneath 57, then subtract.
\(\begin{array}{c}{23 ) \frac{1}{575}} \\ {\frac{23}{34}}\end{array}\)
Because the remainder is larger than the divisor, our estimate is too small. We try again with an estimate of 2.
\(\begin{array}{r}{2} \\ {2 3 \longdiv { 5 7 5 }} \\ {\frac{46}{11}}\end{array}\)
That’s the algorithm. Divide, multiply, then subtract. You may continue only when the remainder is smaller than the divisor.
To continue, bring down the 5, estimate that 115 divided by 23 is 5, then multiply 5 times the divisor and subtract.
\(\begin{array}{c}{25} \\ {2 3 \longdiv { 5 7 5 }} \\ {\frac{46}{115}} \\ {\frac{115}{0}}\end{array}\)
Because the remainder is zero, 575/23 = 25.
Exercise
Divide 980/35
- Answer
-
28
Application — Counting Rectangular Arrays
Consider the rectangular array of stars in Figure 1.15. To count the number of stars in the array, we could use brute force, counting each star in the array one at a time, for a total of 20 stars. However, as we have four rows of five stars each, it is much faster to multiply: 4 · 5 = 20 stars.

Application — Area
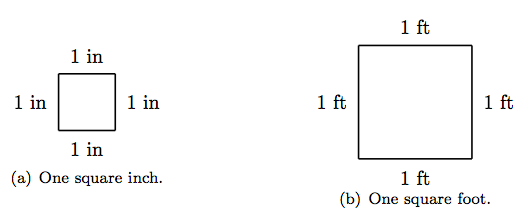
In Figure 1.16(a), pictured is one square inch (1 in2), a square with one inch on each side. In Figure 1.16(b), pictured is one square foot (1 ft2), a square with one foot on each side. Both of these squares are measures of area. Now, consider the rectangle shown in Figure 1.17. The length of this rectangle is four inches (4 in) and the width is three inches (3 in).
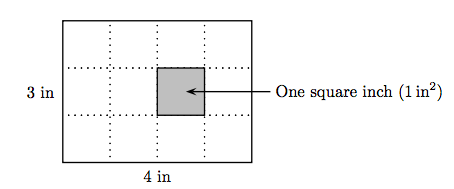
To find the area of the figure, we can count the individual units of area that make up the area of the rectangle, twelve square inches (12 in2) in all. However, as we did in counting the stars in the array in Figure 1.15, it is much faster to note that we have three rows of four square inches. Hence, it is much faster to multiply the number of squares in each row by the number of squares in each column: 4·3 = 12 square inches.
The argument presented above leads to the following rule for finding the area of a rectangle.
Area of a Rectangle
Let L and W represent the length and width of a rectangle, respectively.
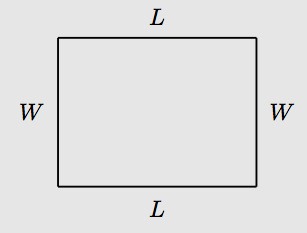
To find the area of the rectangle, calculate the product of the length and width. That is, if A represents the area of the rectangle, then the area of the rectangle is given by the formula
A = LW.
Example 4
A rectangle has width 5 feet and length 12 feet. Find the area of the rectangle.
Solution
Substitute L = 12 ft and W = 5 ft into the area formula.
A = LW
= (12 ft)(5 ft)
= 60 ft2
Hence, the area of the rectangle is 60 square feet.
Exercise
A rectangle has width 17 inches and length 33 inches. Find the area of the rectangle.
- Answer
-
561 square inches
Exercises
In Exercises 1-4 use number line diagrams as shown in Figure 1.6 to depict the multiplication.
1. 2 · 4.
2. 3 · 4.
3. 4 · 2.
4. 4 · 3.
In Exercises 5-16, state the property of multiplication depicted by the given identity.
5. 9 · 8=8 · 9
6. 5 · 8=8 · 5
7. 8 · (5 · 6) = (8 · 5) · 6
8. 4 · (6 · 5) = (4 · 6) · 5
9. 6 · 2=2 · 6
10. 8 · 7=7 · 8
11. 3 · (5 · 9) = (3 · 5) · 9
12. 8 · (6 · 4) = (8 · 6) · 4
13. 21 · 1 = 21
14. 39 · 1 = 39
15. 13 · 1 = 13
16. 44 · 1 = 44
In Exercises 17-28, multiply the given numbers.
17. 78 · 3
18. 58 · 7
19. 907 · 6
20. 434 · 80
21. 128 · 30
22. 454 · 90
23. 799 · 60
24. 907 · 20
25. 14 · 70
26. 94 · 90
27. 34 · 90
28. 87 · 20
In Exercises 29-40, multiply the given numbers.
29. 237 · 54
30. 893 · 94
31. 691 · 12
32. 823 · 77
33. 955 · 89
34. 714 · 41
35. 266 · 61
36. 366 · 31
37. 365 · 73
38. 291 · 47
39. 955 · 57
40. 199 · 33
41. Count the number of objects in the array.

42. Count the number of objects in the array.

43. Count the number of objects in the array.

44. Count the number of objects in the array.

In Exercises 45-48, find the area of the rectangle having the given length and width.
45. L = 50 in, W = 25 in
46. L = 48 in, W = 24 in
47. L = 47 in, W = 13 in
48. L = 19 in, W = 10 in
In Exercises 49-52, find the perimeter of the rectangle having the given length and width.
49. L = 25 in, W = 16 in
50. L = 34 in, W = 18 in
51. L = 30 in, W = 28 in
52. L = 41 in, W = 25 in
53. A set of beads costs 50 cents per dozen. What is the cost (in dollars) of 19 dozen sets of beads?
54. A set of beads costs 60 cents per dozen. What is the cost (in dollars) of 7 dozen sets of beads?
55. If a math tutor worked for 47 hours and was paid $15 each hour, how much money would she have made?
56. If a math tutor worked for 46 hours and was paid $11 each hour, how much money would he have made?
57. There are 12 eggs in one dozen, and 12 dozen in one gross. How many eggs are in a shipment of 24 gross?
58. There are 12 eggs in one dozen, and 12 dozen in one gross. How many eggs are in a shipment of 11 gross?
59. If bricks weigh 4 kilograms each, what is the weight (in kilograms) of 5000 bricks?
60. If bricks weigh 4 pounds each, what is the weight (in pounds) of 2000 bricks?
In Exercises 61-68, which of the following four expressions differs from the remaining three?
61. \(\frac{30}{5}\), 30 ÷ 5, \(5 \longdiv { 3 0 }\), 5 ÷ 30
62. \(\frac{12}{2}\), 12 ÷ 2, \(2 \longiv{12}\), 2 ÷ 12
63. \(\frac{8}{2}\), 8 ÷ 2, \(2 \longdiv{8}\), \(8 \longdiv{2}\)
64. \(\frac{8}{4}\), 8 ÷ 4, \(4 \longdiv { 8 }\), \(8 \longdiv { 4 }\)
65. \(2 \longdiv { 14 }\), \(14 \longdiv { 2 }\), \(\frac{14}{2}\) , 14 ÷ 2
66. \(9 \longdiv { 54 }\), \(54 \longdiv { 9 }\), \(\frac{54}{9}\) , 54 ÷ 9
67. \(3 \longdiv { 24 }\), 3 ÷ 24, \(\frac{24}{3}\), 24 ÷ 3
68. \(3 \longdiv { 15 }\), 3 ÷ 15, \(\frac{15}{3}\), 15 ÷ 3
In Exercises 69-82, simplify the given expression. If the answer doesn’t exist or is undefined, write “undefined”.
69. 0 ÷ 11
70. 0 ÷ 5
71. 17 ÷ 0
72. 24 ÷ 0
73. 10 · 0
74. 20 · 0
75. \(\frac{7}{0}\)
76. \(\frac{23}{0}\)
77. \(16 \longdiv { 0 }\)
78. \(25 \longdiv { 0 }\)
79. \(\frac{0}{24}\)
80. \(\frac{0}{22}\)
81. \(0 \longdiv { 0 }\)
82. 0 ÷ 0
In Exercises 83-94, divide the given numbers.
83. \(\frac{2816}{44}\)
84. \(\frac{1998}{37}\)
85. \(\frac{2241}{83}\)
86. \(\frac{2716}{97}\)
87. \(\frac{3212}{73}\)
88. \(\frac{1326}{17}\)
89. \(\frac{8722}{98}\)
90. \(\frac{1547}{91}\)
91. \(\frac{1440}{96}\)
92. \(\frac{2079}{27}\)
93. \(\frac{8075}{85}\)
94. \(\frac{1587}{23}\)
In Exercises 95-106, divide the given numbers.
95. \(\frac{17756}{92}\)
96. \(\frac{46904}{82}\)
97. \(\frac{11951}{19}\)
98. \(\frac{22304}{41}\)
99. \(\frac{18048}{32}\)
100. \(\frac{59986}{89}\)
101. \(\frac{29047}{31}\)
102. \(\frac{33264}{86}\)
103. \(\frac{22578}{53}\)
104. \(\frac{18952}{46}\)
105. \(\frac{12894}{14}\)
106. \(\frac{18830}{35}\)
107. A concrete sidewalk is laid in square blocks that measure 6 feet on each side. How many blocks will there be in a walk that is 132 feet long?
108. A concrete sidewalk is laid in square blocks that measure 5 feet on each side. How many blocks will there be in a walk that is 180 feet long?
109. One boat to the island can take 5 people. How many trips will the boat have to take in order to ferry 38 people to the island? (Hint: Round up your answer.)
110. One boat to the island can take 4 people. How many trips will the boat have to take in order to ferry 46 people to the island? (Hint: Round up your answer.)
111. If street lights are placed at most 145 feet apart, how many street lights will be needed for a street that is 4 miles long, assuming that there are lights at each end of the street? (Note: 1 mile = 5280 feet.)
112. If street lights are placed at most 70 feet apart, how many street lights will be needed for a street that is 3 miles long, assuming that there are lights at each end of the street? (Note: 1 mile = 5280 feet.)
113. A concrete sidewalk is laid in square blocks that measure 4 feet on each side. How many blocks will there be in a walk that is 292 feet long?
114. A concrete sidewalk is laid in square blocks that measure 5 feet on each side. How many blocks will there be in a walk that is 445 feet long?
115. One boat to the island can take 3 people. How many trips will the boat have to take in order to ferry 32 people to the island? (Hint: Round up your answer.)
116. One boat to the island can take 4 people. How many trips will the boat have to take in order to ferry 37 people to the island? (Hint: Round up your answer.)
117. If street lights are placed at most 105 feet apart, how many street lights will be needed for a street that is 2 miles long, assuming that there are lights at each end of the street? (Note: 1 mile = 5280 feet.)
118. If street lights are placed at most 105 feet apart, how many street lights will be needed for a street that is 3 miles long, assuming that there are lights at each end of the street? (Note: 1 mile = 5280 feet.)
119. Writing articles. Eli writes an average of 4 articles a day, five days a week, to support product sales. How many articles does Eli write in one week?
120. Machine gun. A 0.50-caliber antiaircraft machine gun can fire 800 rounds each minute. How many rounds could fire in three minutes? Associated Press Times-Standard 4/15/09
121. Laps. The swimming pool at CalCourts is 25 yards long. If one lap is up and back again, how many yards has Wendell swam doing 27 laps?
122. Refrigerator wattage. A conventional refrigerator will run about 12 hours each day can use 150 Watts of power each hour. How many Watts of power will a refrigerator use over the day?
123. Horse hay. A full-grown horse should eat a minimum of 12 pounds of hay each day and may eat much more depending on their weight. How many pounds minimum would a horse eat over a year?
124. College costs. After a $662 hike in fees, Califormia residents who want to attend the University of California as an undergraduate should expect to pay $8,700 in for the upcoming academic year 2009- 2010. If the cost were to remain the same for the next several years, how much should a student expect to pay for a four-year degree program at a UC school?
125. Non-resident costs. Nonresident undergraduates who want to attend a University of California college should expect to pay about $22,000 for the upcoming academic year. Assuming costs remain the same, what can a four-year degree cost?
126. Student tax. The mayer of Providence, Rhode Island wants to tax its 25,000 Brown University students $150 each to contribute to tax receipts saying students should pay for the resources they use just like the town residents. How many dollars would the mayer generate?
127. New iceberg. A new iceberg, shaved off a glacier after a collision with another iceberg, measures about 48 miles long and 28 miles wide. What’s the approximate area of the new iceberg? Associated PressTimes-Standard 02/27/10 2 Huge icebergs set loose off Antarctica’s coast.
128. Solar panels. One of the solar panels on the International Space Station is 34 meters long and 11 meters wide. If there are eight of these, what’s the total area for solar collection?
129. Sidewalk. A concrete sidewalk is to be 80 foot long and 4 foot wide. How much will it cost to lay the sidewalk at $8 per square foot?
130. Hay bales. An average bale of hay weighs about 60 pounds. If a horse eats 12 pounds of hay a day, how many days will one bale feed a horse?
131. Sunspots. Sunspots, where the sun’s magnetic field is much higher, usually occur in pairs. If the total count of sunspots is 72, how many pairs of sunspots are there?
Answers
1. \(2 \cdot 4=\underbrace{4+4}_{2 \text { times }}=8\)
3. \(4 \cdot 2=\underbrace{2+2+2+2}_{4 \text { times }}=8\)
5. Commutative property of multiplication
7. Associative property of multiplication
9. Commutative property of multiplication
11. Associative property of multiplication
13. Multiplicative identity property
15. Multiplicative identity property
17. 234
19. 5442
21. 3840
23. 47940
25. 980
27. 3060
29. 12798
31. 8292
33. 84995
35. 16226
37. 26645
39. 54435
41. 64
43. 56
45. 1250 in2
47. 611 in2
49. 82 in
51. 116 in
53. 9.50
55. 705
57. 3456
59. 20000
61. 5 ÷ 30
63. \(8 \sqrt{2}\)
65. \(14 \sqrt{2}\)
67. 3 ÷ 24
69. 0
71. Undefined
73. 0
75. Undefined
77. 0
79. 0
81. Undefined
83. 64
85. 27
87. 44
89. 89
91. 15
93. 95
95. 193
97. 629
99. 564
101. 937
103. 426
105. 921
107. 22
109. 8
111. 147
113. 73
115. 11
117. 102
119. 20 articles
121. 1350 yards
123. 4380 pounds of hay
125. $88,000
127. 1344 mi2
129. $2,560
131. 36


