1.4: Prime Factorization
- Page ID
- 22462
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the statement 3 · 4 = 12, the number 12 is called the product, while 3 and 4 are called factors.
Find all whole number factors of 18.
Solution
We need to find all whole number pairs whose product equals 18. The following pairs come to mind.
1 · 18 = 18 and 2 · 9 = 18 and 3 · 6 = 18.
Hence, the factors of 18 are (in order) 1, 2, 3, 6, 9, and 18.
Find all whole number factors of 21.
- Answer
-
1, 3, 7, and 21
Divisibility
In Example 1, we saw 3 · 6 = 18, making 3 and 6 factors of 18. Because division is the inverse of multiplication, that is, division by a number undoes the multiplication of that number, this immediately provides
18 ÷ 6 = 3 and 18 ÷ 3=6.
That is, 18 is divisible by 3 and 18 is divisible by 6. When we say that 18 is divisible by 3, we mean that when 18 is divided by 3, there is a zero remainder.
Let a and b be whole numbers. Then a is divisible by b if and only if the remainder is zero when a is divided by b. In this case, we say that “b is a divisor of a.”
Find all whole number divisors of 18.
Solution
In Example 1, we saw that 3 · 6 = 18. Therefore, 18 is divisible by both 3 and 6 (18 ÷ 3 = 6 and 18 ÷ 6 = 3). Hence, when 18 is divided by 3 or 6, the remainder is zero. Therefore, 3 and 6 are divisors of 18. Noting the other products in Example 1, the complete list of divisors of 18 is 1, 2, 3, 6, 9, and 18.
Find all whole number divisors of 21.
- Answer
-
1, 3, 7, and 21.
Example 1 and Example 2 show that when working with whole numbers, the words factor and divisor are interchangeable.
If c = a · b, then a and b are called factors of c. Both a and b are also called divisors of c.
Divisibility Tests
There are a number of very useful divisibility tests.
Divisible by 2. If a whole number ends in 0, 2, 4, 6, or 8, then the number is called an even number and is divisible by 2. Examples of even numbers are 238 and 1,246 (238 ÷ 2 = 119 and 1, 246 ÷ 2 = 623). A number that is not even is called an odd number. Examples of odd numbers are 113 and 2,339.
Divisible by 3. If the sum of the digits of a whole number is divisible by 3, then the number itself is divisible by 3. An example is 141. The sum of the digits is 1 + 4 + 1 = 6, which is divisible by 3. Therefore, 141 is also divisible by 3 (141 ÷ 3 = 47).
Divisible by 4. If the number represented by the last two digits of a whole number is divisible by 4, then the number itself is divisible by 4. An example is 11,524. The last two digits represent 24, which is divisible by 4 (24 ÷ 4 = 6). Therefore, 11,524 is divisible by 4 (11, 524 ÷ 4=2, 881).
Divisible by 5. If a whole number ends in a zero or a 5, then the number is divisible by 5. Examples are 715 and 120 (715÷5 = 143 and 120÷5 = 24).
Divisible by 6. If a whole number is divisible by 2 and by 3, then it is divisible by 6. An example is 738. First, 738 is even and divisible by 2. Second, 7+3+8=18, which is divisible by 3. Hence, 738 is divisible by 3. Because 738 is divisible by both 2 and 3, it is divisible by 6 (738 ÷ 6 = 123).
Divisible by 8. If the number represented by the last three digits of a whole number is divisible by 8, then the number itself is divisible by 8. An example is 73,024. The last three digits represent the number 24, which is divisible by 8 (24÷8 = 3). Thus, 73,024 is also divisible by 8 (73, 024÷8 = 9, 128).
Divisible by 9. If the sum of the digits of a whole number is divisible by 9, then the number itself is divisible by 9. An example is 117. The sum of the digits is 1 + 1 + 7 = 9, which is divisible by 9. Hence, 117 is divisible by 9 (117 ÷ 9 = 13).
Prime Numbers
We begin with the definition of a prime number.
A whole number (other than 1) is a prime number if its only factors (divisors) are 1 and itself. Equivalently, a number is prime if and only if it has exactly two factors (divisors).
Which of the whole numbers 12, 13, 21, and 37 are prime numbers?
Solution
- The factors (divisors) of 12 are 1, 2, 3, 4, 6, and 12. Hence, 12 is not a prime number.
- The factors (divisors) of 13 are 1 and 13. Because its only divisors are 1 and itself, 13 is a prime number.
- The factors (divisors) of 21 are 1, 3, 7, and 21. Hence, 21 is not a prime number.
- The factors (divisors) of 37 are 1 and 37. Because its only divisors are 1 and itself, 37 is a prime number.
Which of the whole numbers 15, 23, 51, and 59 are prime numbers?
- Answer
-
23 and 59
List all the prime numbers less than 20.
Solution
The prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17, and 19.
You try it!
List all the prime numbers less than 100.
If a whole number is not a prime number, then it is called a composite number.
Is the whole number 1,179 prime or composite?
Solution
Note that 1 + 1 + 7 + 9 = 18, which is divisible by both 3 and 9. Hence, 3 and 9 are both divisors of 1,179. Therefore, 1,179 is a composite number.
Is the whole number 2,571 prime or composite?
- Answer
-
Composite
Factor Trees
We will now learn how to express a composite number as a unique product of prime numbers. The most popular device for accomplishing this goal is the factor tree.
Express 24 as a product of prime factors.
Solution
We use a factor tree to break 24 down into a product of primes.

At each level of the tree, break the current number into a product of two factors. The process is complete when all of the “circled leaves” at the bottom of the tree are prime numbers. Arranging the factors in the “circled leaves” in order,
24 = 2 · 2 · 2 · 3.
The final answer does not depend on product choices made at each level of the tree. Here is another approach.
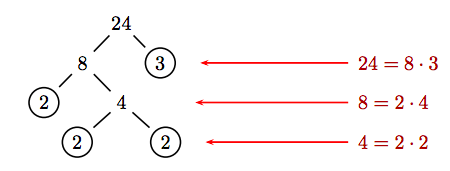
The final answer is found by including all of the factors from the “circled leaves” at the end of each branch of the tree, which yields the same result, namely 24 = 2 · 2 · 2 · 3.
Alternate Approach
Some favor repeatedly dividing by 2 until the result is no longer divisible by 2. Then try repeatedly dividing by the next prime until the result is no longer divisible by that prime. The process terminates when the last resulting quotient is equal to the number 1.
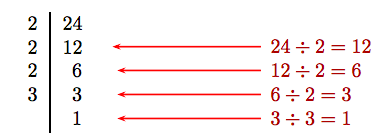
The first column reveals the prime factorization; i.e., 24 = 2 · 2 · 2 · 3.
Express 36 as a product of prime factors.
- Answer
-
2 · 2 · 3 · 3.
The fact that the alternate approach in Example 6 yielded the same result is significant.
Every whole number can be uniquely factored as a product of primes.
This result guarantees that if the prime factors are ordered from smallest to largest, everyone will get the same result when breaking a number into a product of prime factors.
Exponents
We begin with the definition of an exponential expression.
The expression am is defined to mean
\( a^{m}=\underbrace{a \cdot a \cdot \ldots \cdot a}_{m \text { times }}\)
The number a is called the base of the exponential expression and the number m is called the exponent. The exponent m tells us to repeat the base a as a factor m times.
Evaluate 25, 23, and 52.
Solution
- In the case of 25, we have
25 = 2 · 2 · 2 · 2 · 2
= 32.
- In the case of 33, we have
33 = 3 · 3 · 3
= 27.
- In the case of 52, we have
52 = 5 · 5
= 25.
Evaluate: 35.
- Answer
-
243.
Express the solution to Example 6 in compact form using exponents.
Solution
In Example 6, we determined the prime factorization of 24.
24 = 2 · 2 · 2 · 3
Because 2 · 2 · 2=23, we can write this more compactly.
24 = 23 · 3
Prime factor 54.
- Answer
-
2 · 3 · 3 · 3
Evaluate the expression 23 · 32 · 52.
Solution
First raise each factor to the given exponent, then perform the multiplication in order (left to right).
23 · 32 · 52 = 8 · 9 · 25
= 72 · 25
= 1800
Evaluate: 33 · 52.
- Answer
-
675
Application
A square is a rectangle with four equal sides.
Let s represent the length of each side of a square.
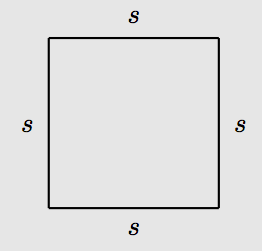
Because a square is also a rectangle, we can find the area of the square by multiplying its length and width. However, in this case, the length and width both equal s, so A = (s)(s) = s2. Hence, the formula for the area of a square is
A = s2.
The edge of a square is 13 centimeters. Find the area of a square.
Solution
Substitute s = 13 cm into the area formula.
A = s2
= (13 cm)2
= (13 cm)(13 cm)
= 169 cm2
Hence, the area of the square is 169 cm2; i.e., 169 square centimeters.
The edge of a square is 15 meters. Find the area of a square.
- Answer
-
225 square meters
Exercises
In Exercises 1-12, find all divisors of the given number.
1. 30
2. 19
3. 83
4. 51
5. 91
6. 49
7. 75
8. 67
9. 64
10. 87
11. 14
12. 89
In Exercises 13-20, which of the following numbers is not divisible by 2?
13. 117, 120, 342, 230
14. 310, 157, 462, 160
15. 30, 22, 16, 13
16. 382, 570, 193, 196
17. 105, 206, 108, 306
18. 60, 26, 23, 42
19. 84, 34, 31, 58
20. 66, 122, 180, 63
In Exercises 21-28, which of the following numbers is not divisible by 3?
21. 561, 364, 846, 564
22. 711, 850, 633, 717
23. 186, 804, 315, 550
24. 783, 909, 504, 895
25. 789, 820, 414, 663
26. 325, 501, 945, 381
27. 600, 150, 330, 493
28. 396, 181, 351, 606
In Exercises 29-36, which of the following numbers is not divisible by 4?
29. 3797, 7648, 9944, 4048
30. 1012, 9928, 7177, 1592
31. 9336, 9701, 4184, 2460
32. 2716, 1685, 2260, 9788
33. 9816, 7517, 8332, 7408
34. 1788, 8157, 7368, 4900
35. 1916, 1244, 7312, 7033
36. 7740, 5844, 2545, 9368
In Exercises 37-44, which of the following numbers is not divisible by 5?
37. 8920, 4120, 5285, 9896
38. 3525, 7040, 2185, 2442
39. 8758, 3005, 8915, 3695
40. 3340, 1540, 2485, 2543
41. 2363, 5235, 4145, 4240
42. 9030, 8000, 5445, 1238
43. 1269, 5550, 4065, 5165
44. 7871, 9595, 3745, 4480
In Exercises 45-52, which of the following numbers is not divisible by 6?
45. 328, 372, 990, 528
46. 720, 288, 148, 966
47. 744, 174, 924, 538
48. 858, 964, 930, 330
49. 586, 234, 636, 474
50. 618, 372, 262, 558
51. 702, 168, 678, 658
52. 780, 336, 742, 312
In Exercises 53-60, which of the following numbers is not divisible by 8?
53. 1792, 8216, 2640, 5418
54. 2168, 2826, 1104, 2816
55. 8506, 3208, 9016, 2208
56. 2626, 5016, 1392, 1736
57. 4712, 3192, 2594, 7640
58. 9050, 9808, 8408, 7280
59. 9808, 1232, 7850, 7912
60. 3312, 1736, 9338, 3912
In Exercises 61-68, which of the following numbers is not divisible by 9?
61. 477, 297, 216, 991
62. 153, 981, 909, 919
63. 153, 234, 937, 675
64. 343, 756, 927, 891
65. 216, 783, 594, 928
66. 504, 279, 307, 432
67. 423, 801, 676, 936
68. 396, 684, 567, 388
In Exercises 69-80, identify the given number as prime, composite, or neither.
69. 19
70. 95
71. 41
72. 88
73. 27
74. 61
75. 91
76. 72
77. 21
78. 65
79. 23
80. 36
In Exercises 81-98, find the prime factorization of the natural number.
81. 224
82. 320
83. 108
84. 96
85. 243
86. 324
87. 160
88. 252
89. 32
90. 128
91. 360
92. 72
93. 144
94. 64
95. 48
96. 200
97. 216
98. 392
In Exercises 99-110, compute the exact value of the given exponential expression.
99. 52 · 41
100. 23 · 41
101. 01
102. 13
103. 33 · 02
104. 33 · 22
105. 41
106. 52
107. 43
108. 42
109. 33 · 12
110. 52 · 23
In Exercises 111-114, find the area of the square with the given side.
111. 28 inches
112. 31 inches
113. 22 inches
114. 13 inches
Create factor trees for each number in Exercises 115-122. Write the prime factorization for each number in compact form, using exponents.
115. 12
116. 18
117. 105
118. 70
119. 56
120. 56
121. 72
122. 270
123. Sieve of Eratosthenes. This exercise introduces the Sieve of Eratosthenes, an ancient algorithm for finding the primes less than a certain number n, first created by the Greek mathematician Eratosthenes. Consider the grid of integers from 2 through 100.
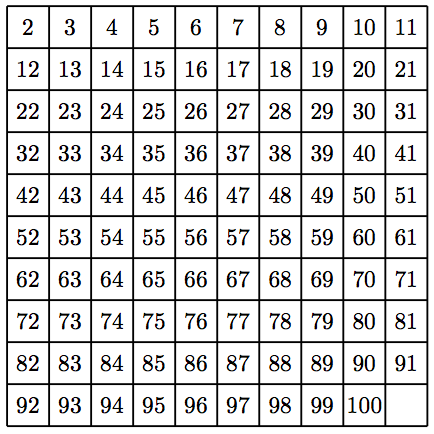
To find the primes less than 100, proceed as follows.
i) Strike out all multiples of 2 (4, 6, 8, etc.)
ii) The list’s next number that has not been struck out is a prime number.
iii) Strike out from the list all multiples of the number you identified in step (ii).
iv) Repeat steps (ii) and (iii) until you can no longer strike any more multiples.
v) All unstruck numbers in the list are primes.
Answers
1. 1, 2, 3, 5, 6, 10, 15, 30
3. 1, 83
5. 1, 7, 13, 91
7. 1, 3, 5, 15, 25, 75
9. 1, 2, 4, 8, 16, 32, 64
11. 1, 2, 7, 14
13. 117
15. 13
17. 105
19. 31
21. 364
23. 550
25. 820
27. 493
29. 3797
31. 9701
33. 7517
35. 7033
37. 9896
39. 8758
41. 2363
43. 1269
45. 328
47. 538
49. 586
51. 658
53. 5418
55. 8506
57. 2594
59. 7850
61. 991
63. 937
65. 928
67. 676
69. prime
71. prime
73. composite
75. composite
77. composite
79. prime
81. 2 · 2 · 2 · 2 · 2 · 7
83. 2 · 2 · 3 · 3 · 3
85. 3 · 3 · 3 · 3 · 3
87. 2 · 2 · 2 · 2 · 2 · 5
89. 2 · 2 · 2 · 2 · 2
91. 2 · 2 · 2 · 3 · 3 · 5
93. 2 · 2 · 2 · 2 · 3 · 3
95. 2 · 2 · 2 · 2 · 3
97. 2 · 2 · 2 · 3 · 3 · 3
99. 100
101. 0
103. 0
105. 4
107. 64
109. 27
111. 784 in2
113. 484 in2
115. 12 = 22 · 3
117. 105 = 3 · 5 · 7
119. 56 = 23 · 7
121. 72 = 23 · 32
123. Unstruck numbers are primes: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97


