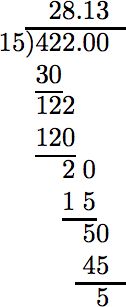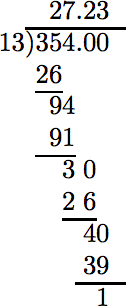6.2: Introduction to Ratios and Rates
- Page ID
- 22495
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We use ratios to compare two numeric quantities or quantities with the same units.
A ratio is the quotient of two numerical quantities or two quantities with the same physical units.
For example, ancient Greek geometers believed that the most pleasing rectangle to the eye had length and width such that the ratio of length to width was a specific number, called the Golden Ratio, approximately equal to 1.6180339887.... Architects to this day use this ratio in their designs.
There are a number of equivalent ways of expressing ratios, three of which we will use in this text: fraction notation, “to” notation, and “colon” notation.
- 3/4 is a ratio, read as “the ratio of 3 to 4.”
- 3 to 4 is a ratio, read as “the ratio of 3 to 4.”
- 3:4 is a ratio, read as “the ratio of 3 to 4.”
Express each of the following ratios as a fraction reduced to lowest terms: (a) 36 to 24, and (b) 0.12 : 0.18.
Solution
(a) To express the ratio “36 to 24” as a fraction, place 36 over 24 and reduce.
\[ \begin{aligned} \frac{36}{24} = \frac{3 \cdot \textcolor{red}{12}}{2 \cdot \textcolor{red}{12}} ~ & \textcolor{red}{ \text{ Factor.}} \\ = \frac{3 \cdot \cancel{ \textcolor{red}{12}}}{2 \cdot \cancel{ \textcolor{red}{12}}} ~ & \textcolor{red}{ \text{ Cancel common factor.}} \\ = \frac{3}{2} \end{aligned}\nonumber \]
Thus, the ratio 36 to 24 equals 3/2.
(b) To express the ratio “0.12:0.18” as a fraction, place 0.12 over 0.18 and reduce.
\[ \begin{aligned} \frac{0.12}{0.18} = \frac{(0.18) \textcolor{red}{(100)}}{(0.18) \textcolor{red}{(100)}} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 100.}} \\ = \frac{12}{18} ~ & \textcolor{red}{ \text{ Move each decimal 2 places right.}} \\ = \frac{2 \cdot \textcolor{red}{6}}{3 \cdot \textcolor{red}{6}} ~ & \textcolor{red}{ \text{ Factor.}} \\ = \frac{2 \cdot \cancel{ \textcolor{red}{6}}}{3 \cdot \cancel{ \textcolor{red}{6}}} ~ & \textcolor{red}{ \text{Cancel.}} \\ \frac{2}{3} \end{aligned}\nonumber \]
Thus, the ratio 0.12:0.18 equals 2/3.
Express 0.12 : 0.3 as a fraction reduced to lowest terms.
- Answer
-
2/5
For the rectangle that follows, express the ratio of length to width as a fraction reduced to lowest terms.
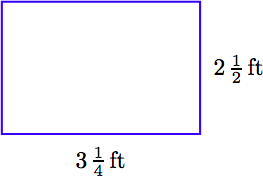
Solution.
The ratio length to width can be expressed as a fraction and reduced as follows.
\[ \begin{aligned} \frac{ \text{length}}{ \text{width}} = \frac{3 \frac{1}{4} \text{ ft}}{2 \frac{1}{2} \text{ ft}} ~ & \textcolor{red}{ \text{ Length to width as a fraction.}} \\ = \frac{3 \frac{1}{4} \cancel{ \text{ ft}}}{2 \frac{1}{2} \cancel{ \text{ ft}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{ \frac{13}{4}}{ \frac{5}{2}} ~ & \textcolor{red}{ \text{ Mixed to improper fractions.}} \end{aligned}\nonumber \]
Invert and multiply, factor, and cancel common factors.
\[ \begin{aligned} = \frac{13}{4} \cdot \frac{2}{5} ~ & \textcolor{red}{ \text{ Invert and multiply.}} \\ = \frac{26}{20} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = \frac{13 \cdot \textcolor{red}{2}}{10 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Factor numerator and denominator.}} \\ = \frac{13 \cdot \cancel{ \textcolor{red}{2}}}{10 \cdot \cancel{ \textcolor{red}{2}}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{13}{10} \end{aligned}\nonumber \]
Hence, the ratio length to width is 13/10.
A rectangle has length \(8 \frac{1}{4}\) inches and width \(3 \frac{1}{2}\) inches. Express the ratio of length to width as a fraction reduced to lowest terms.
- Answer
-
33/14
Rates
We now introduce the concept of rate, a special type of ratio.
A rate is a quotient of two measurements with different units.
The physical interpretation of a rate in terms of its units is an important skill.
An automobile travels 224 miles on 12 gallons of gasoline. Express the ratio distance traveled to gas consumption as a fraction reduced to lowest terms. Write a short sentence explaining the physical significance of your solution. Include units in your description.
Solution
Place miles traveled over gallons of gasoline consumed and reduce.
\[ \begin{aligned} \frac{224 \text{ mi}}{12 \text{ gal}} = \frac{56 \cdot \textcolor{red}{4} \text{ mi}}{3 \cdot \textcolor{red}{4} \text{ gal}} ~ & \textcolor{red}{ \text{ Factor.}} \\ = \frac{56 \cdot \cancel{ \textcolor{red}{4}} \text{ mi}}{3 \cdot \cancel{ \textcolor{red}{4}} \text{ gal}} ~ & \textcolor{red}{ \text{ Cancel common factor.}} \\ = \frac{56 \text{ mi}}{3 \text{ gal}} \end{aligned}\nonumber \]
Thus, the rate is 56 miles to 3 gallons of gasoline. In plain-speak, this means that the automobile travels 56 miles on 3 gallons of gasoline.
Lanny travels 180 kilometers on 14 liters of gasoline. Express the ratio distance traveled to gas consumption as a fraction reduced to lowest terms.
- Answer
-
90/7 kilometers per litre
Unit Rates
When making comparisons, it is helpful to have a rate in a form where the denominator is 1. Such rates are given a special name.
A unit rate is a rate whose denominator is 1.
Herman drives 120 miles in 4 hours. Find his average rate of speed.
Solution
Place the distance traveled over the time it takes to drive that distance.
\[ \begin{aligned} \frac{120 \text{ miles}}{4 \text{ hours}} = \frac{30 \text{ miles}}{1 \text{ hour}} ~ & \textcolor{red}{ \text{ Divide: } 120/4 = 30.} \\ = 30 \text{ miles/hour} \end{aligned}\nonumber \]
Hence, Herman’s average rate of speed is 30 miles per hour.
Jacob drives 120 kilometers in 3 hours. Find his average rate of speed.
- Answer
-
40 kilometers per hour
Aditya works 8.5 hours and receives $95 for his efforts. What is his hourly salary rate?
Solution
Let’s place money earned over hours worked to get the following rate:
\[ \frac{95 \text{ dollars}}{8.5 \text{ hours}}\nonumber \]
We will get a much better idea of Aditya’s salary rate if we express the rate with a denominator of 1. To do so, divide. Push the decimal in the divisor to the far right, then move the decimal an equal number of places in the dividend. As we are dealing with dollars and cents, we will round our answer to the nearest hundredth.

Because the test digit is greater than or equal to 5, we add 1 to the rounding digit and truncate; i.e., 95/8.5 ≈ 11.18. Hence,
\[ \begin{aligned} \frac{95 \text{ dollars}}{8.5 \text{ hours}} = \frac{11.18 \text{ dollars}}{1 \text{ hour}} ~ & \textcolor{red}{ \text{ Divide: } 95/8.5 \approx 11.18.} \\ = 11.18 \text{ dollars/hour.} \end{aligned}\nonumber \]
That is, his salary rate is 11.18 dollars per hour.
Frannie works 5.5 hours and receives $120 for her efforts. What is her hourly salary rate? Round your answer to the nearest penny.
- Answer
-
$21.82 per hour
One automobile travels 422 miles on 15 gallons of gasoline. A second automobile travels 354 miles on 13 gallons of gasoline. Which automobile gets the better gas mileage?
Solution
Decimal division (rounded to the nearest tenth) reveals the better gas mileage.
|
In the case of the first automobile, we get the following rate: \[ \frac{422 \text{ mi}}{15 \text{gal}}\nonumber \] Divide.
To the nearest tenth, 28.1. |
In the case of the second autombile, we get the following rate: \[ \frac{354 \text{ mi}}{13 \text{ gal}}\nonumber \] Divide.
To the nearest tenth, 27.2. |
In the case of the first automobile, the mileage rate is 28.1 mi/1 gal, which can be read “28.1 miles per gallon.” In the case of the second automobile, the mileage rate is 27.2 mi/1 gal, which can be read “27.2 miles per gallon.” Therefore, the first automobile gets the better gas mileage.
Alicia works 8 hours and makes $100. Connie works 10 hours and makes $122. Which woman works at the larger hourly rate?
- Answer
-
Alicia
Exercises
In Exercises 1-24, express the given ratio as a fraction reduced to lowest terms.
1. 0.14 : 0.44
2. 0.74 : 0.2
3. 0.05 : 0.75
4. 0.78 : 0.4
5. 0.1:0.95
6. 0.93 : 0.39
7. \(2 \frac{2}{9}\) : \(1 \frac{1}{3}\)
8. \(3 \frac{2}{3} : 2 \frac{4}{9}\)
9. 0.36 : 0.6
10. 0.58 : 0.42
11. 15 : 21
12. 77 : 121
13. \(2 \frac{8}{9}\) : \(2 \frac{2}{3}\)
14. \(1 \frac{2}{3}\) : \(3 \frac{8}{9}\)
15. \(3 \frac{8}{9}\) : \(2 \frac{1}{3}\)
16. \(1 \frac{5}{9}\) : \(1 \frac{1}{3}\)
17. \(2 \frac{5}{8}\) : \(1 \frac{3}{4}\)
18. \(2 \frac{4}{9}\) : \(1 \frac{1}{3}\)
19. 10 : 35
20. 132 : 84
21. 9 : 33
22. 35 : 10
23. 27 : 99
24. 12 : 28
25. One automobile travels 271.8 miles on 10.1 gallons of gasoline. A second automobile travels 257.9 miles on 11.1 gallons of gasoline. Which automobile gets the better gas mileage?
26. One automobile travels 202.9 miles on 13.9 gallons of gasoline. A second automobile travels 221.6 miles on 11.8 gallons of gasoline. Which automobile gets the better gas mileage?
27. Todd is paid 183 dollars for 8.25 hours work. What is his hourly salary rate, rounded to the nearest penny?
28. David is paid 105 dollars for 8.5 hours work. What is his hourly salary rate, rounded to the nearest penny?
29. An automobile travels 140 miles in 4 hours. Find the average rate of speed.
30. An automobile travels 120 miles in 5 hours. Find the average rate of speed.
31. Judah is paid 187 dollars for 8 hours work. What is his hourly salary rate, rounded to the nearest penny?
32. Judah is paid 181 dollars for 8.75 hours work. What is his hourly salary rate, rounded to the nearest penny?
33. One automobile travels 234.2 miles on 10.8 gallons of gasoline. A second automobile travels 270.5 miles on 10.8 gallons of gasoline. Which automobile gets the better gas mileage?
34. One automobile travels 297.6 miles on 10.7 gallons of gasoline. A second automobile travels 298.1 miles on 12.6 gallons of gasoline. Which automobile gets the better gas mileage?
35. An automobile travels 180 miles in 5 hours. Find the average rate of speed.
36. An automobile travels 220 miles in 5 hours. Find the average rate of speed.
37. Antarctic trek. Seven women on a 562-mile Antarctic ski trek reached the South Pole 38 days after they began their adventure. What was the ladies’ average rate of speed per day? Round your result to the nearest tenth of a mile. Associated Press-Times-Standard 12/31/09 After 562-mile ski trek, seven women reach the South Pole.
Answers
1. \(\frac{7}{22}\)
3. \(\frac{1}{15}\)
5. \(\frac{2}{19}\)
7. \(\frac{5}{3}\)
9. \(\frac{3}{5}\)
11. \(\frac{5}{7}\)
13. \(\frac{13}{12}\)
15. \(\frac{5}{3}\)
17. \(\frac{3}{2}\)
19. \(\frac{2}{7}\)
21. \(\frac{3}{11}\)
23. \(\frac{3}{11}\)
25. The first automobile has the better mileage per gallon.
27. 22.18 dollars/hr
29. 35 mi/hr
31. 23.38 dollars/hr
33. The second automobile has the better mileage per gallon.
35. 36 mi/hr
37. 14.8 miles per day