6.3: Introduction to Proportion
- Page ID
- 22496
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In Section 6.1, we introduced the concepts or ratio and rate. In this section, we equate these ratios in a construct called a proportion.
A proportion is a statement that equates two ratios or rates.
For example, each of the equations
\[\frac{1}{3} = \frac{2}{6}, ~ \frac{15 \text{ miles}}{2 \text{ hours}} = \frac{30 \text{ miles}}{4 \text{ hours}}, \text{ and } \frac{a}{b} = \frac{c}{d}\nonumber \]
compare two ratios or rates and is a proportion.
The proportion
\[ \frac{1}{3} = \frac{2}{6}\nonumber \]
is read “one is to three as two is to six.” The four numbers that make up this proportion are called the terms of the proportion and are ordered in a natural manner.
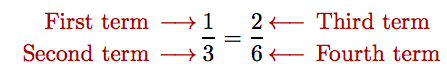
The first and fourth terms are called the extremes of the proportion. The second and third terms are called the means of the proportion.
In the proportion
\[ \frac{a}{b} = \frac{c}{d},\nonumber \]
the terms a and d are the extremes; the terms b and c are the means.

If we multiply both sides of the proportion by the common denominator,
\[bd \left(\frac{a}{b} \right) = bd \left( \frac{c}{d} \right)\nonumber \]
then cancel,
\[ \cancel{b} d \left( \frac{a}{\cancel{b}} \right) = b \cancel{d} \left( \frac{c}{\cancel{d}} \right)\nonumber \]
we get the following result.
\[ad = bc\nonumber \]
This leads to the following observation.
In the proportion
\[ \frac{a}{b} = \frac{c}{d}\nonumber \]
the product of the means equals the product of the extremes. That is,
\[ad = bc.\nonumber \]
We can get an equivalent result using a technique called cross multiplication.

Which of the following is a valid proportion: (a) \(\frac{2}{3} = \frac{7}{12}\), or (b) \(\frac{4}{9} = \frac{12}{27}\).
Solution
(a) Cross multiply

to get
24 = 21.
Hence, the product of the extremes does not equal the product of the means, so 2/3=7/12 is not a valid proportion.
(b) Cross multiply

to get
108 = 108.
Hence, the product of the extremes equals the product of the means, so 4/9 = 12/27 is a valid proportion.
Is the following a valid proportion? \(\frac{4}{3} = \frac{16}{11}\)
- Answer
-
No
Solving Proportions
We already have all the tools needed to solve proportions. Let’s begin with the first example.
Solve the proportion for x: \(\frac{3}{4} = \frac{x}{12}\).
Solution
Cross multiply, then solve the resulting equation.
\[ \begin{aligned} \frac{3}{4} = \frac{x}{12} ~ & \textcolor{red}{ \text{ Original proportion.}} \\ 4 \cdot x = 3 \cdot 12 ~ & \textcolor{red}{ \text{ Products of means and extremes are equal.}} \\ 4x = 36 ~ & \textcolor{red}{ \text{ Simplify.}} \\ \frac{4x}{4} = \frac{36}{4} ~ & \textcolor{red}{ \text{ Divide both sides by 4.}} \\ x = 9 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Check
Substitute 9 for x into the original proportion and check.
\[ \begin{aligned} \frac{3}{4} = \frac{x}{12} ~ & \textcolor{red}{ \text{ Original proportion.}} \\ \frac{3}{4} = \frac{9}{12} ~ & \textcolor{red}{ \text{ Substitute 9 for } x.} \end{aligned}\nonumber \]
Cross multiply.

Thus, the solution 9 checks.
Solve the proportion for n: \(\frac{2}{3} = \frac{n}{9}\)
- Answer
-
6
Solve the proportion for n: \(\frac{3}{2} = \frac{24}{n}\).
Solution
Cross multiply, then solve the resulting equation.
\[ \begin{aligned} \frac{3}{2} = \frac{24}{n} ~ & \textcolor{red}{ \text{ Original proportion.}} \\ 3 \cdot n = 2 \cdot 24 ~ & \textcolor{red}{ \text{ Products of means and extremes are equal.}} \\ 3n = 48 ~ & \textcolor{red}{ \text{ Simplify.}} \\ \frac{3n}{3} = \frac{48}{3} ~ & \textcolor{red}{ \text{ Divide both sides by 3.}} \\ n = 16 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Check
Substitute 16 for n into the original proportion and check.
\[ \begin{aligned} \frac{3}{2} = \frac{24}{n} ~ & \textcolor{red}{ \text{ Original proportion.}} \\ \frac{3}{2} = \frac{24}{16} ~ & \textcolor{red}{ \text{ Substitute 16 for } n.} \end{aligned}\nonumber \]
Cross multiply.

Thus, the solution 16 checks.
Solve the proportion for m: \(\frac{9}{6} = \frac{m}{4}\)
- Answer
-
6
Solve the proportion for x: \(\frac{2x + 1}{15} = \frac{1}{3}\).
Solution
Cross multiply, then solve the resulting equation.
\[ \begin{aligned} \frac{2x+1}{15} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Original proportion.}} \\ 3(2x+1) = 15(1) ~ & \textcolor{red}{ \text{ Products f means and extremes are equal.}} \\ 6x+3 = 15 ~ & \textcolor{red}{ \begin{aligned} \text{ On the left, distribute.} \\ \text{ On the right, multiply.} \end{aligned}} \\ 6x+3-3=15-3 ~ & \textcolor{red}{ \text{ Subtract 3 from both sides.}} \\ 6x=12 ~ & \textcolor{red}{ \text{ Simplify.}} \\ \frac{6x}{6} = \frac{12}{6} ~ & \textcolor{red}{ \text{ Divide both sides by 6.}} \\ x = 2 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Check
We’ll leave it to our readers to check this solution.
Solve the proportion for y: \(\frac{6+2y}{18} = \frac{8}{9}\)
- Answer
-
5
Applications
A number of practical applications involve solving a proportion.
If 5 oranges cost $1.15, what will be the cost for 15 oranges (assuming an equal rate)?
Solution
Let x represent the cost for 15 oranges. Assuming the rate for 5 oranges at $1.15 equals the rate for 15 oranges at an unknown cost x, we set up the following proportion.
\[ \frac{5}{1.15} = \frac{15}{x}\nonumber \]
Cross multiply
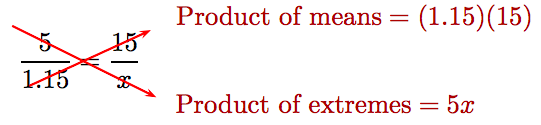
to get
\[5x = 17.25.\nonumber \]
Solve for x.
\[\begin{aligned} \frac{5x}{5} = \frac{17.25}{5} \\ x = 3.45 \end{aligned}\nonumber \]
Thus, 15 oranges cost $3.45.
If 7 apples cost $3.15, how much will 10 apples cost (assuming an equal rate)?
- Answer
-
$4.50
When setting up a proportion, check to make sure that both numerators have the same units and both denominators have the same units.
For example, in Example 5, both numerators have “oranges” as units and both denominators have “dollars” as units.
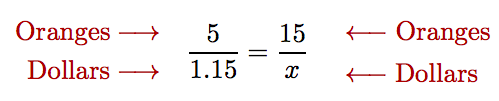
This proportion is set up correctly, because both numerators have the same units and both denominators have the same units. On the other hand, if we had set the proportion up incorrectly as follows,
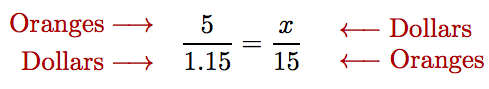
a quick check of the units reveals the error; i.e., the numerators have different units and the denominators have different units. Checking units helps us avoid errors!
Dylan and David are planning a backpacking trip in Yosemite National Park. On their map, the legend indicates that 1.2 centimeters represents 2 miles. How long is their trip if the route measures 10.6 centimeters on the map? Round your answer to the nearest tenth of a mile.
Solution
Let’s set up the proportion with units.
\[\frac{1.2 \text{ cm}}{2 \text{ mi}} = \frac{10.6 \text{ cm}}{x \text{ mi}}\nonumber \]
Note how including the units aids in the setup of the proportion. Now, let’s drop the units and solve for x.
\[ \begin{aligned} \frac{1.2}{2} = \frac{10.6}{x} ~ & \textcolor{red}{ \text{ Original proportion.}} \\ 1.2x = (2)(10.6) ~ & \textcolor{red}{ \text{ Cross multiply.}} \\ 1.2x = 21.2 ~ & \textcolor{red}{ \text{ Simplify right-side hand.}} \\ \frac{1.2x}{1.2} = \frac{21.2}{1.2} ~ & \textcolor{red}{ \text{ Divide both sides by 1.2.}} \\ x \approx 17.66 ~ & \textcolor{red}{ \text{ On the right: Divide.}} \end{aligned}\nonumber \]
We carried the division on the right one decimal place past the tenths place. The rounding digit is a 6 and the following test digit is a 6. Add 1 to the rounding digit and truncate.
To the nearest tenth of a mile, the backpacking route is approximately 17.7 miles.
Eloise and Susannah are planning a trip is Sequoia National Park. On their map, 3 inches represents 50 miles. How long is their trip if the route measures \(4 \frac{1}{2}\) inches on the map?
- Answer
-
75 miles
A recipe making 2 dozen cookies requires \(1 \frac{3}{4}\) cups of flour, among other ingredients. If the baker wishes to make twice that number of cookies, how much flour is required?
Solution
Twice 2 dozen is 4 dozen cookies. Let x represent the amount of flour needed for 4 dozen cookies. Assuming an equal rate for 2 dozen cookies (2 dozen requires 1 3 4 cups of flour), we set up the following proportion. Again, using units helps us craft the correct proportion.
\[\frac{2 \text{ dozen}}{1 \frac{3}{4} \text{ cups}} = \frac{4 \text{ dozen}}{x \text{ cups}}\nonumber \]
Note how including the units aids in the setup of the proportion. Now, let’s drop the units and solve for x.
\[ \begin{aligned} \frac{2}{1 \frac{3}{4}} = \frac{4}{x} ~ & \textcolor{red}{ \text{ Original proportion.}} \\ 2x = 1 \frac{3}{4} \cdot 4 ~ & \textcolor{red}{ \text{ Cross multiply.}} \\ 2x = \frac{7}{4} \cdot 4 ~ & \textcolor{red}{ \text{ Change to improper fraction.}} \\ 2x = 7 ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]
Divide both sides of the equation by 2 and finish.
\[ \begin{aligned} \frac{2x}{2} = \frac{7}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ x = \frac{7}{2} \end{aligned}\nonumber \]
Change the improper fraction to a mixed fraction. Thus, it will take \(3 \frac{1}{2}\) cups of flour to make 4 dozen cookies.
Dough for 3 pizzas requires \(8 \frac{1}{2}\) cups of flour. If the baker wishes to make 9 pizzas, how many cups of flour are required?
- Answer
-
\(25 \frac{1}{2}\) cups
Exercises
In Exercises 1-12, which of the following is a true proportion?
1. \(\frac{9}{7} = \frac{27}{21}, ~ \frac{4}{3} = \frac{9}{7}, ~ \frac{7}{2} = \frac{8}{9}, ~ \frac{4}{8} = \frac{9}{6}\)
2. \(\frac{6}{7} = \frac{18}{21}, ~ \frac{2}{3} = \frac{8}{6}, ~ \frac{4}{3} = \frac{3}{2}, ~ \frac{8}{9} = \frac{3}{8}\)
3. \(\frac{7}{6} = \frac{28}{24}, ~ \frac{5}{6} = \frac{5}{4}, ~ \frac{9}{5} = \frac{7}{3}, ~ \frac{9}{2} = \frac{8}{9}\)
4. \(\frac{7}{6} = \frac{2}{8}, ~ \frac{4}{5} = \frac{5}{7}, ~ \frac{3}{4} = \frac{15}{20}, ~ \frac{8}{4} = \frac{8}{7}\)
5. \(\frac{6}{5} = \frac{24}{20}, ~ \frac{7}{3} = \frac{2}{4}, ~ \frac{2}{4} = \frac{2}{6}, ~ \frac{5}{2} = \frac{2}{8}\)
6. \(\frac{9}{8} = \frac{4}{3}, ~ \frac{5}{7} = \frac{10}{14}, ~ \frac{8}{6} = \frac{5}{4}, ~ \frac{8}{5} = \frac{2}{6}\)
7. \(\frac{3}{5} = \frac{2}{8}, ~ \frac{3}{7} = \frac{6}{14}, ~ \frac{5}{6} = \frac{2}{4}, ~ \frac{7}{4} = \frac{5}{9}\)
8. \(\frac{7}{3} = \frac{7}{6}, ~ \frac{4}{7} = \frac{8}{14}, ~ \frac{5}{3} = \frac{7}{8}, ~ \frac{5}{7} = \frac{6}{9}\)
9. \(\frac{5}{4} = \frac{25}{20}, ~ \frac{9}{3} = \frac{9}{6}, ~ \frac{7}{4} = \frac{3}{6}, ~ \frac{3}{5} = \frac{9}{4}\)
10. \(\frac{7}{6} = \frac{6}{9}, ~ \frac{7}{3} = \frac{2}{5}, ~ \frac{6}{7} = \frac{30}{35}, ~ \frac{4}{7} = \frac{2}{8}\)
11. \(\frac{9}{7} = \frac{4}{3}, ~ \frac{9}{4} = \frac{7}{9}, ~ \frac{3}{5} = \frac{6}{10}, ~ \frac{3}{9} = \frac{9}{5}\)
12. \(\frac{4}{3} = \frac{8}{7}, ~ \frac{2}{6} = \frac{5}{8}, ~ \frac{7}{2} = \frac{3}{6}, ~ \frac{9}{4} = \frac{36}{16}\)
In Exercises 13-36, solve the given proportion.
13. \(\frac{17}{3} = \frac{x}{18}\)
14. \(\frac{16}{5} = \frac{x}{20}\)
15. \(\frac{6x + 10}{6} = \frac{11}{3}\)
16. \(\frac{4x + 8}{12} = \frac{5}{3}\)
17. \(\frac{17}{9} = \frac{x}{18}\)
18. \(\frac{8}{9} = \frac{x}{18}\)
19. \(\frac{11}{2} = \frac{x}{8}\)
20. \(\frac{11}{4} = \frac{x}{8}\)
21. \(\frac{7x + 15}{15} = \frac{10}{3}\)
22. \(\frac{7x + 3}{8} = \frac{5}{4}\)
23. \(\frac{11}{2} = \frac{x}{10}\)
24. \(\frac{19}{6} = \frac{x}{18}\)
25. \(\frac{5x + 8}{12} = \frac{2}{3}\)
26. \(\frac{3x + 12}{6} = \frac{3}{2}\)
27. \(\frac{2}{15} = \frac{24}{x}\)
28. \(\frac{7}{8} = \frac{14}{x}\)
29. \(\frac{3}{16} = \frac{6}{x}\)
30. \(\frac{4}{21} = \frac{12}{x}\)
31. \(\frac{5}{22} = \frac{20}{x}\)
32. \(\frac{3}{22} = \frac{21}{x}\)
33. \(\frac{2x + 10}{6} = \frac{14}{3}\)
34. \(\frac{2x + 9}{9} = \frac{13}{3}\)
35. \(\frac{7}{2} = \frac{21}{x}\)
36. \(\frac{2}{15} = \frac{18}{x}\)
37. If 13 dog bones cost $1.97, what will be the cost for 7 dog bones (assuming an equal rate)? Round your answer to the nearest penny.
38. If 2 watermelons cost $3.89, what will be the cost for 11 watermelons (assuming an equal rate)? Round your answer to the nearest penny.
39. If 7 bananas cost $2.55, what will be the cost for 14 bananas (assuming an equal rate)? Round your answer to the nearest penny.
40. If 2 apples cost $2.05, what will be the cost for 8 apples (assuming an equal rate)? Round your answer to the nearest penny.
41. If 13 oranges cost $3.61, what will be the cost for 11 oranges (assuming an equal rate)? Round your answer to the nearest penny.
42. If 3 watermelons cost $1.05, what will be the cost for 9 watermelons (assuming an equal rate)? Round your answer to the nearest penny.
43. If 3 dog bones cost $1.23, what will be the cost for 13 dog bones (assuming an equal rate)? Round your answer to the nearest penny.
44. If 3 watermelons cost $4.41, what will be the cost for 7 watermelons (assuming an equal rate)? Round your answer to the nearest penny.
45. If 3 apples cost $3.24, what will be the cost for 13 apples (assuming an equal rate)? Round your answer to the nearest penny.
46. If 6 apples cost $3.43, what will be the cost for 7 apples (assuming an equal rate)? Round your answer to the nearest penny.
47. If 4 dog bones cost $1.03, what will be the cost for 8 dog bones (assuming an equal rate)? Round your answer to the nearest penny.
48. If 4 oranges cost $4.28, what will be the cost for 3 oranges (assuming an equal rate)? Round your answer to the nearest penny.
49. Two rolls. In Haiti, two flat rolls cost 5 gourdes, about 12 cents. How many cents would 20 rolls cost? Associated Press-Times-Standard 02/18/10 Haiti’s earthquake camps turning into shanty towns.
50. Turbines. As proposed, the Shell Wind Energy project consists of 25 ridge-top turbines that can generate up to 50 megawatts, or enough to supply electricity to about 1, 000 homes. Estimate the number of ridge-top turbines that would be needed to supply electricity to 70, 000 homes, the approximate number of properties in Humboldt County, CA. John Driscoll Times-Standard 12/24/09 Wind power project goes under analysis.
51. Dumptrucks. U.S. Highway 199 had a landslide where as much as 3, 000 cubic yards of material fell on the road, reportedly requiring about 200 large dumptrucks to remove. Only a week earlier, 40, 000 cubic yards of material fell on Highway 96. Estimate the number of dumptrucks needed for that slide rounded to the nearest whole number. Associated Press-Times-Standard 03/09/10 Another highway closed by slide.
52. Timber sales. Alaska’s 26, 000 square mile Tongass National Forest plan allows for timber sales of up to 267 million board-feet per year – enough for nearly 27, 000 two-bedroom homes, but demand for timber is far short of that. Less than 25 million board-feet was logged in the forest in 2009. Forest Service officials have said they hope to increase logging in the Tongass to about 100 million board-feet per year. Associated Press-Times-Standard 02/18/10 Industry loses lawsuit over logging in Alaska.
i) Estimate the number of 2-bedroom homes that 25 million board-feet of timber would build.
ii) How many 2-bedroom homes would 100 million board-feet of timber build?
53. Costly spill. In Australia, penalties on ships causing oil spills are approximately $1.75 million Australian dollars, equivalent to about $1.64 million US dollars. After an oil tanker was grounded onto a coral reef, Australian officials are considering raising the fine to $10 million Australian dollars. What will the new fine be in US dollars? Round your answer to the nearest hundredth of a million dollars. Associated Press-Times-Standard 04/13/10 Ship that leaked oil on Great Barrier Reef removed.
Answers
1. \(\frac{9}{7} = \frac{27}{21}\) is a proportion
3. \(\frac{7}{6} = \frac{28}{24}\) is a proportion
5. \(\frac{6}{5} = \frac{24}{20}\) is a proportion
7. \(\frac{3}{7} = \frac{6}{14}\) is a proportion
9. \(\frac{5}{4} = \frac{25}{20}\) is a proportion
11. \(\frac{3}{5} = \frac{6}{10}\) is a proportion
13. 102
15. 2
17. 34
19. 44
21. 5
23. 55
25. 0
27. 180
29. 32
31. 88
33. 9
35. 6
37. $1.06
39. $5.10
41. $3.05
43. $5.33
45. $14.04
47. $2.06
49. $0.48
51. 2, 667 loads
53. $9.37 million US dollars


