6.4: Unit Conversion - American System
- Page ID
- 22497
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section we will develop a technique for converting units used in the American system. We begin with a discussion of common measurements of length in the United States.
Units of Length
The most common units of length are the inch, foot, yard, and mile. Our focus will be on the technique used to convert from one unit of length to another.
Facts relating common units of length.
- 1 foot (ft) = 12 inches (in)
- 1 yard (yd) = 3 feet (ft)
- 1 mile (mi) = 5280 feet (ft)
Take for example, the fact that there are 3 feet in 1 yard, which can be stated as an equation, using the common abbreviations for feet (ft) and yards (yd).
3 ft = 1 yd
If we divide both sides of the equation by 3 ft,
\[ \frac{3 \text{ ft}}{3 \text{ ft}} = \frac{1 \text{ yd}}{3 \text{ ft}}, \nonumber\nonumber \]
or equivalently,
\[1 = \frac{1 \text{ yd}}{3 \text{ ft}}. \nonumber\nonumber \]
The key observation is the fact that the ratio 1 yd/3 ft equals the number 1. Consequently, multiplying by the “conversion factor” 1 yd/3 ft is equivalent to multiplying by 1. This can be used to change a measurement in feet to yards.
Change 36 feet to yards.
Solution
Multiply by the conversion factor 1 yd/3 ft.
\[ \begin{aligned} 36 \text{ ft} = 36 \text{ ft} \cdot 1 ~ & \textcolor{red}{ \text{ Multiplicative Identity Property.}} \\ = 36 \text{ ft} \cdot \frac{1 \text{ yd}}{3 \text{ ft}} ~ & \textcolor{red}{ \text{ Replace 1 with 1 yd/3 ft.}} \\ = 36 \cancel{ \text{ ft}} \cdot \frac{1 \text{ yd}}{3 \cancel{ \text{ ft}}} ~ & \textcolor{red}{ \text{ Cancel common unit.}} \\ = \frac{36 \cdot 1}{3} \text{ yd} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ = \frac{36}{3} \text{ yd} ~ & \textcolor{red}{ \text{ Simplify.}} \\ = 12 \text{ yd} ~ & \textcolor{red}{ \text{ Divide.}} \end{aligned}\nonumber \]
Hence, 36 feet equals 12 yards.
Change 81 feet to yards.
- Answer
-
27 yards
On the other hand, we can start again with
\[3 \text{ ft} = 1 \text{ yd}\nonumber \]
and divide both sides of the equation by 1 yd.
\[\frac{3 \text{ ft}}{1 \text{ yd}} = \frac{1 \text{ yd}}{1 \text{ yd}} \nonumber\nonumber \]
This gives the conversion factor
\[ \frac{3 \text{ ft}}{1 \text{ yd}} = 1.\nonumber\nonumber \]
The key observation is the fact that the ratio 3 ft/1 yd equals the number 1. Consequently, multiplying by the “conversion factor” 3 ft/1 yd is equivalent to multiplying by 1. This can be used to change a measurement in yards to feet.
Change 18 yards to feet.
Solution
Multiply by the conversion factor 3 ft/1 yd.
\[ \begin{aligned} 18 \text{ yd} = 18 \text{ yd} \cdot 1 ~ & \textcolor{red}{ \text{ Multiplicative Identity Property.}} \\ = 18 \text{ yd} \cdot \frac{1 \text{ ft}}{1 \text{ yd}} ~ & \textcolor{red}{ \text{ Replace 1 with 3 ft/1 yd.} \\ = 18 \cancel{ \text{ yd}} \cdot \frac{3 \text{ ft}}{1 \cancel{ \text{ yd}} ~ & \textcolor{red}{ \text{ Cancel common unit.}} \\ = \frac{18 \cdot 3}{1} \text{ ft} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 54 \text{ ft} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Hence, 18 yards equals 54 feet.
Change 15 yards to feet.
- Answer
-
45 feet
Another common comparison is the fact that there are 12 inches in 1 foot. This can be represented as an equation using the common abbreviation for inches (in) and feet (ft).
\[12 \text{ in} = 1 \text{ ft}\nonumber \]
Dividing both sides by 12 in
\[ \frac{12 \text{ in}}{12 \text{ in}} = \frac{1 \text{ ft}}{12 \text{ in}},\nonumber \]
yields the conversion factor
\[1 = \frac{1 \text{ ft}}{12 \text{ in}}.\nonumber \]
The key observation is the fact that the ratio 1 ft/12 in equals the number 1. Consequently, multiplying by the “conversion factor” 1 ft/12 in is equivalent to multiplying by 1. This can be used to change a measurement in inches to feet.
Change 24 inches to feet.
Solution
Multiply by the conversion factor 1 ft/12 in.
\[ \begin{aligned} 24 \text{ in} = 24 \text{ in} \cdot 1 ~ & \textcolor{red}{ \text{ Multiplicative Identity Property.}} \\ = 24 \text{ in} \cdot \frac{1 \text{ ft}}{12 \text{ in}} ~ & \textcolor{red}{ \text{ Replace 1 with 1 ft/12 in.}} \\ = 24 \cancel{ \text{ in}} \cdot \frac{1 \text{ in}}{12 \cancel{ \text{ in}}} ~ & \textcolor{red}{ \text{ Cancel common unit.}} \\ = \frac{24 \cdot 1}{12} \text{ ft} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 2 \text{ ft} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Hence, 24 inches equals 2 feet.
Change 48 inches to feet.
- Answer
-
4 feet
We provide a summary of conversion factors for units of length in Table 6.1.
| Convert | Conversion Factor | Convert | Conversion Factor |
|---|---|---|---|
| feet to inches | 12 in/1 ft | inches to feet | 1 ft/12 in |
| yards to feet | 3 ft/1 yd | feet to yards | 1 yd/3 ft |
| miles to feet | 5280 ft/1 mi | feet to miles | 1 mi/5280 ft |
Some conversions require more than one application of a conversion factor.
Change 4 yards to inches.
Solution
We multiply by a chain of conversion factors, the first to change yards to feet, the second to change feet to inches.
\[ \begin{aligned} 4 \text{ yd} = 4 \text{ yd} \cdot \frac{3 \text{ ft}}{1 \text{ yd}} \cdot \frac{12 \text{ in}}{1 \text{ ft}} ~ & \textcolor{red}{ \text{ Multiply by conversion factors.}} \\ = 4 \cancel{ \text{ yd}} \cdot \frac{3 \cancel{ \text{ ft}}{1 \cancel{ \text{ yd}} \cdot \frac{12 \text{ in}}{1 \cancel{ \text{ ft}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{4 \cdot 3 \cdot 12}{1 \cdot 1} \text{ in} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 144 \text{ in} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Hence, 4 yards equals 144 inches.
Change 8 yards to inches.
- Answer
-
288 inches
Change 2 miles to yards.
Solution
We multiply by a chain of conversion factors, the first to change miles to feet, the second to change feet to yards.
\[ \begin{aligned} 2 \text{ mi} = 2 \text{ mi} \cdot \frac{5280 \text{ ft}}{1 \text{ mi}} \cdot \frac{1 \text{ yd}}{3 \text{ ft}} ~ & \textcolor{red}{ \text{ Multiply by conversion factors.}} \\ = 2 \cancel{ \text{ mi}} \cdot \frac{5280 \cancel{ \text{ ft}}}{1 \cancel{ \text{ mi}}} \cdot \frac{1 \text{ yd}}{3 \cancel{ \text{ ft}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{2 \cdot 5280 \cdot 1}{1 \cdot 3} \text{ yd} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 3520 \text{ yd} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Hence, 2 miles equals 3,520 yards.
Change 5 miles to yards.
- Answer
-
8,800 yards
Units of Weight
The most common units of weight are the ounce, pound, and ton. Our focus will remain on how to convert from one unit to another.
Facts relating common units of weight.
- 1 pound (lb) = 16 ounces (oz)
- 1 ton = 2000 pounds (lb)
The above facts lead to the conversion factors in Table 6.2.
| Convert | Conversion Factor | Convert | Conversion Factor |
|---|---|---|---|
| pounds to ounces | 16 oz/1 lb | ounces to pounds | 1 lb/16 oz |
| tons to pounds | 2000 lb/1 ton | pounds to tons | 1 ton/2000 lb |
Change \(2 \frac{1}{2}\) pounds to ounces.
Solution
Multiply by the appropriate conversion factor.
\[ \begin{aligned} 2 \frac{1}{2} \text{ lb} = 2 \frac{1}{2} \text{ lb} \cdot \frac{16 \text{ oz}}{1 \text{ lb}} ~ & \textcolor{red}{ \text{ Multiply by conversion factor.}} \\ = 2 \frac{1}{2} \cancel{ \text{ lb}} \cdot \frac{16 \text{ oz}}{1 \cancel{ \text{ lb}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \left( 2 \frac{1}{2} \cdot 16 \right) \text{ oz } & \textcolor{red}{ \text{ Multiply fractions.}} \\ = \left( \frac{5}{2} \cdot 16 \right) \text{ oz } & \textcolor{red}{ \text{ Mixed to improper fraction.}} \\ = \frac{80}{2} \text{ oz } & \textcolor{red}{ \text{ Multiply.}} \\ = 40 \text{ oz } & \textcolor{red}{ \text{ Divide.}} \end{aligned}\nonumber \]
Hence, \(2 \frac{1}{2}\) pounds equals 40 ounces.
Change \(6 \frac{1}{4}\) pounds to ounces.
- Answer
-
100 ounces
Change 3.2 tons to ounces.
Solution
This exercise requires multiplying by a chain of conversion factors.
\[ \begin{aligned} 3.2 \text{ ton } = 3.2 \text{ ton } \cdot \frac{2000 \text{ lb}}{1 \text{ ton}} \cdot \frac{16 \text{ oz}}{1 \text{ lb}} ~ & \textcolor{red}{ \text{ Multiply by conversion factors.}} \\ = 3.2 \cancel{ \text{ ton}} \cdot \frac{2000 \cancel{ \text{ lb}}}{1 \cancel{ \text{ ton}}} \cdot \frac{16 \text{ oz}}{1 \cancel{ \text{ lb}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{3.2 \cdot 2000 \cdot 16}{1 \cdot 1} \text{ oz } & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 102,400 \text{ oz } & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Hence, 3.2 tons equals 102,400 ounces.
Change 4.1 tons to ounces.
- Answer
-
128,000 ounces
Units of Volume
The most common units of volume are fluid ounces, cups, pints, quarts, and gallons. We will focus on converting from one unit to another.
Facts relating common units of volume.
- 1 cup (c) = 8 fluid ounces (fl oz)
- 1 pint (pt) = 2 cups (c)
- 1 quart (qt) = 2 pints (pt)
- 1 gallon (gal) = 4 quarts (qt)
These facts lead to the conversion factors listed in Table 6.3.
| Convert | Conversion Factor | Convert | Conversion Factor |
|---|---|---|---|
| cups to ounces | 8 fl oz/1 c | ounces to cups | 1c/8 fl oz |
| pints to cups | 2 c/1 pt | cups to pints | 1 pt/2 c |
| quarts to pints | 2 pt/1 qt | pints to quarts | 1 qt/2 pt |
| gallons to quarts | 4 qt/1 gal | quarts to gallons | 1 gal/4 qt |
Change 5.6 gallons to pints.
Solution
This exercise requires multiplying by a chain of conversion factors.
\[ \begin{aligned} 5.6 \text{ gal } = 5.6 \text{ gal } \cdot \frac{4 \text{ qt}}{1 \text{ gal}} \cdot \frac{2 \text{ pt}}{1 \text{ qt}} ~ & \textcolor{red}{ \text{ Multiply by conversion factors.}} \\ = 5.6 \cancel{\text{ gal }} \cdot \frac{4 \cancel{\text{ qt}}}{1 \cancel{ \text{ gal}}} \cdot \frac{2 \text{ pt}}{1 \cancel{ \text{ qt}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{5.6 \cdot 4 \cdot 2}{1 \cdot 1} \text{ pt } & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 44.8 \text{ pt } & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Hence, 5.6 gallons equals 44.8 pints.
Change 3.2 gallons to pints.
- Answer
-
25.6 pints
Units of Time
The most common units of time are seconds, minutes, hours, days, and years.
Facts relating common units of time.
- 1 minute (min) = 60 seconds (s)
- 1 hour (hr) = 60 minutes (min)
- 1 day (day) = 24 hours (hr)
- 1 year (yr) = 365 days (day)
These facts lead to the conversion factors in Table 6.4.
| Convert | Conversion Factor | Convert | Conversion Factor |
|---|---|---|---|
| minutes to seconds | 60 s/1 min | seconds to minutes | 1 min/60 s |
| hours to minutes | 60 min/1 hr | minutes to hours | 1 hr/60 min |
| days to hours | 24 hr/1 day | hours to days | 1 day/24 hr |
| years to days | 365 day/1 yr | days to years | 1 yr/365 day |
How many seconds in a year?
Solution
A chain of conversion factors is needed.
\[ \begin{aligned} 1 \text{ yr } = 1 \text{ yr } \cdot \frac{365 \text{ day}}{1 \text{ yr}} \cdot \frac{24 \text{ hr}}{1 \text{ day}} \cdot \frac{60 \text{ min}}{1 \text{ hr}} \cdot \frac{60 \text{ s}}{1 \text{ min}} ~ & \textcolor{red}{ \text{ Conversion factors.}} \\ = 1 \cancel{ \text{ yr}} \cdot \frac{365 \cancel{ \text{ day}}}{1 \cancel{ \text{ yr}}} \cdot \frac{24 \cancel{ \text{ hr}}}{1 \cancel{ \text{ day}}} \cdot \frac{60 \cancel{ \text{ min}}}{1 \cancel{ \text{ hr}}} \cdot \frac{60 \text{ s}}{1 \cancel{ \text{ min}}} & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{1 \cdot 365 \cdot 24 \cdot 60 \cdot 60}{1 \cdot 1 \cdot 1 \cdot 1} \text{ s } & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 31,536,000 \text{ s } & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Thus, 1 year equals 31,536,000 seconds.
How many seconds in a day?
- Answer
-
86,400 seconds
Converting Units of Speed
Ever wonder how fast a baseball is moving?
A professional pitcher can throw a baseball at 95 miles per hour. How fast is this in feet per second? Round your answer to the nearest foot per second.
Solution
There are 5280 feet in a mile, 60 minutes in an hour, and 60 seconds in a minute.
\[ \begin{aligned} 95 \frac{ \text{mi}}{ \text{h}} \approx 95 \frac{ \text{mi}}{\text{h}} \cdot \frac{5280 \text{ ft}}{1 \text{ mi}} \cdot \frac{1 \text{ h}}{60 \text{ min}} \cdot \frac{1 \text{ min}}{60 \text{ s}} ~ & \textcolor{red}{ \text{ Conversion factors.}} \\ \approx 95 \frac{ \cancel{\text{mi}}}{\cancel{\text{h}}} \cdot \frac{5280 \text{ ft}}{1 \cancel{\text{ mi}}} \cdot \frac{1 \cancel{\text{ h}}}{60 \cancel{\text{ min}}} \cdot \frac{1 \cancel{\text{ min}}}{60 \text{ s}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ \approx \frac{95 \cdot 5280 \cdot 1 \cdot 1}{1 \cdot 60 \cdot 60} \frac{ \text{ft}}{\text{s}} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ \approx 139.3 \frac{ \text{ft}}{\text{s}} ~ & \textcolor{red}{ \text{ Multiply and divide.}} \end{aligned}\nonumber \]
To round to the nearest foot per second, identify the rounding and test digits.
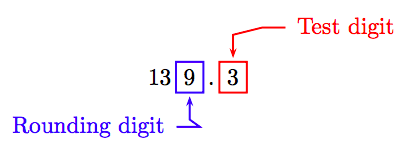
Because the test digit is less than 5, leave the rounding digit alone and truncate. Thus, to the nearest foot per second, the speed is approximately 139 feet per second.
Whew! Since the batter stands at home plate, which is about 60 feet from where the pitch is delivered, the batter has less than 1/2 a second to react to the pitch!
A women’s softball pitcher can throw her fastball at 60 miles per hour. How fast is this in feet per second? Round your answer to the nearest foot per second.
- Answer
-
88 feet per second
Exercises
1. Change 8 yards to feet.
2. Change 60 yards to feet.
3. Change 261 feet to yards.
4. Change 126 feet to yards.
5. Change 235 inches to yards. Round your answer to the nearest tenth of a yard.
6. Change 244 inches to yards. Round your answer to the nearest tenth of a yard.
7. Change 141 feet to yards.
8. Change 78 feet to yards.
9. Change 2.8 miles to feet.
10. Change 4.9 miles to feet.
11. Change 104 inches to yards. Round your answer to the nearest tenth of a yard.
12. Change 101 inches to yards. Round your answer to the nearest tenth of a yard.
13. Change 168,372 inches to miles, correct to the nearest tenth of a mile.
14. Change 198,550 inches to miles, correct to the nearest tenth of a mile.
15. Change 82 feet to inches.
16. Change 80 feet to inches.
17. Change 2.9 yards to inches. Round your answer to the nearest inch.
18. Change 4.5 yards to inches. Round your answer to the nearest inch.
19. Change 25,756 feet to miles. Round your answer to the nearest tenth of a mile.
20. Change 19,257 feet to miles. Round your answer to the nearest tenth of a mile.
21. Change 5 yards to feet.
22. Change 20 yards to feet.
23. Change 169,312 inches to miles, correct to the nearest tenth of a mile.
24. Change 162,211 inches to miles, correct to the nearest tenth of a mile.
25. Change 1.5 yards to inches. Round your answer to the nearest inch.
26. Change 2.1 yards to inches. Round your answer to the nearest inch.
27. Change 360 inches to feet.
28. Change 768 inches to feet.
29. Change 48 inches to feet.
30. Change 528 inches to feet.
31. Change 15,363 feet to miles. Round your answer to the nearest tenth of a mile.
32. Change 8,540 feet to miles. Round your answer to the nearest tenth of a mile.
33. Change 1.7 miles to inches.
34. Change 4.7 miles to inches.
35. Change 3.1 miles to inches.
36. Change 1.8 miles to inches.
37. Change 3.6 miles to feet.
38. Change 3.1 miles to feet.
39. Change 18 feet to inches.
40. Change 33 feet to inches.
41. Change \(5 \frac{1}{8}\) pounds to ounces.
42. Change \(3 \frac{1}{16}\) pounds to ounces.
43. Change 2.4 tons to ounces.
44. Change 3.4 tons to ounces.
45. Change 34 ounces to pounds. Express your answer as a fraction reduced to lowest terms.
46. Change 78 ounces to pounds. Express your answer as a fraction reduced to lowest terms.
47. Change 2.2 tons to pounds.
48. Change 4.8 tons to pounds.
49. Change 70 ounces to pounds. Express your answer as a fraction reduced to lowest terms.
50. Change 20 ounces to pounds. Express your answer as a fraction reduced to lowest terms.
51. Change 9,560 pounds to tons. Round your answer to the nearest tenth of a ton.
52. Change 9,499 pounds to tons. Round your answer to the nearest tenth of a ton.
53. Change \(2 \frac{1}{2}\) pounds to ounces.
54. Change \(7 \frac{1}{16}\) pounds to ounces.
55. Change 5.9 tons to pounds.
56. Change 2.1 tons to pounds.
57. Change 2.5 tons to ounces.
58. Change 5.3 tons to ounces.
59. Change 8,111 pounds to tons. Round your answer to the nearest tenth of a ton.
60. Change 8,273 pounds to tons. Round your answer to the nearest tenth of a ton.
61. Change 4.5625 pints to fluid ounces.
62. Change 2.9375 pints to fluid ounces.
63. Change 32 fluid ounces to pints.
64. Change 160 fluid ounces to pints.
65. Change 3.7 gallons to pints.
66. Change 2.4 gallons to pints.
67. Change 216 pints to gallons.
68. Change 96 pints to gallons.
69. Change 544 fluid ounces to pints.
70. Change 432 fluid ounces to pints.
71. Change 112 pints to gallons.
72. Change 200 pints to gallons.
73. Change 7.7 gallons to pints.
74. Change 5.7 gallons to pints.
75. Change 3.875 pints to fluid ounces.
76. Change 3 pints to fluid ounces.
77. Change 7.8 years to hours.
78. Change 4.7 years to hours.
79. Change 7.6 years to hours.
80. Change 6.6 years to hours.
81. Change 4,025,005 seconds to days. Round your answer to the nearest tenth of a day.
82. Change 4,672,133 seconds to days. Round your answer to the nearest tenth of a day.
83. Change 37,668 hours to years.
84. Change 40,296 hours to years.
85. Change 22,776 hours to years.
86. Change 29,784 hours to years.
87. Change 96 days to seconds.
88. Change 50 days to seconds.
89. Change 40 days to seconds.
90. Change 10 days to seconds.
91. Change 3,750,580 seconds to days. Round your answer to the nearest tenth of a day.
92. Change 4,493,469 seconds to days. Round your answer to the nearest tenth of a day.
93. Change 367 feet per second to miles per hour. Round your answer to the nearest mile per hour.
94. Change 354 feet per second to miles per hour. Round your answer to the nearest mile per hour.
95. Change 442 feet per second to miles per hour. Round your answer to the nearest mile per hour.
96. Change 388 feet per second to miles per hour. Round your answer to the nearest mile per hour.
97. Change 30 miles per hour to feet per second. Round your answer to the nearest foot per second.
98. Change 99 miles per hour to feet per second. Round your answer to the nearest foot per second.
99. Change 106 miles per hour to feet per second. Round your answer to the nearest foot per second.
100. Change 119 miles per hour to feet per second. Round your answer to the nearest foot per second.
101. Strong man. Famed strongman Joe Rollino, who was still bending quarters with his fingers at age 104, once lifted 3, 200 pounds at Coney Island Amusement Park. How many tons did Joe lift that day? Associated Press-Times-Standard 01/12/10 NYC amusement park strongman, 104, killed by van.
102. Earth day. The amount of time it takes the Earth to rotate once around its axis is one day. How many seconds is that?
103. Water break. “The average age of Washington, DC’s water pipes is 76 years, and they are not alone. Every two minutes, somewhere in the country, a pipe breaks.” How many pipes break each year in the US? New York Times 03/14/10 Saving U.S. water and sewer systems could be costly.
Answers
1. 24 feet
3. 87 yards
5. 6.5 yards
7. 47 yards
9. 14,784 feet
11. 2.9 yards
13. 2.7 miles
15. 984 inches
17. 104 inches
19. 4.9 miles
21. 15 feet
23. 2.7 miles
25. 54 inches
27. 30 feet
29. 4 feet
31. 2.9 miles
33. 107,712 inches
35. 196,416 inches
37. 19,008 feet
39. 216 inches
41. 82 ounces
43. 76,800 ounces
45. \(2 \frac{1}{8}\) pounds
47. 4,400 pounds
49. \(4 \frac{3}{8}\) pounds
51. 4.8 tons
53. 40 ounces
55. 11,800 pounds
57. 80,000 ounces
59. 4.1 tons
61. 73 fluid ounces
63. 2 pints
65. 29.6 pints
67. 27 gallons
69. 34 pints
71. 14 gallons
73. 61.6 pints
75. 62 fluid ounces
77. 68,328 hours
79. 66,576 hours
81. 46.6 days
83. 4.3 years
85. 2.6 years
87. 8,294,400 seconds
89. 3,456,000 seconds
91. 43.4 days
93. 250 mi/hr
95. 301 mi/hr
97. 44 ft/s
99. 155 ft/s
101. 1.6 tons
103. 262, 800