6.5: Unit Conversion- Metric System
- Page ID
- 22498
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The metric system of units is the standard system of units preferred by scientists. It is based on the base ten number system and its decimal format is more friendly to users of this system. There is a common set of prefixes adopted by the metric system to indicate a power of ten to apply to the base unit.
This is a list of standard prefixes for the metric system and their meanings.
\[ \begin{array}{c c} \text{deka = 10} & \text{deci = 1/10} \\ \text{hecto = 100} & \text{centi = 1/100} \\ \text{kilo = 1000} & \text{milli = 1/1000} \end{array}\nonumber \]
Thus, for example, a decameter is 10 meters, a hectoliter is 100 liters, and a kilogram is 1000 grams. Similarly, a decimeter is 1/10 of a meter, a centiliter is 1/100 of a liter, and a milligram is 1/1000 of a gram.
Units of Length
The standard measure of length in the metric system is the meter.
Historically, the meter was defined by the French Academy of Sciences as the length between two marks on a platinum-iridium bar, which was designed to represent 110,000,000 of the distance from the equator to the north pole through Paris. In 1983, it was redefined by the International Bureau of Weights and Measures (BIPM) as the distance travelled by light in free space in 1299,792,458 of a second. (Wikipedia)
We can apply the standard prefixes to get the following result.
These units of length are used in the metric system.
| Unit Length | Unit Abbreviation |
|---|---|
| 1 kilometer = 1000 meters | km |
| 1 hectometer = 100 meters | hm |
| 1 dekameter = 10 meters | dam |
| 1 meter | m |
| 1 decimeter = \(\frac{1}{10}\) meter | dm |
| 1 centimeter = \(\frac{1}{100}\) meter | cm |
| 1 millimeter = \(\frac{1}{1000}\) meter | mm |
We can use these facts to build conversion factors as we did in Section 6.3. For example, because
1 km = 1000 m,
we can divide both sides by 1000 m to produce the conversion factor
\[1 = \frac{1 \text{ km}}{1000 \text{ m}}.\nonumber \]
This conversion factor can help change meters into kilometers.
Before using this conversion factor in an example, we repeat here the rules for multiplying and dividing by powers of ten. We will be making heavy use of these rules in this section.
- Multiplying a decimal number by 10n will move the decimal point n places to the right. For example, 3.2567 · 102 = 3.2567 · 100 = 325.67.
- Dividing a decimal number by 10n will move the decimal point n places to the left. For example, 3.2567/102 = 3.2567/100 = 0.032567.
And now the example.
Change 2,326 meters to kilometers.
Solution
Multiply by the conversion factor 1 km/1000m.
\[ \begin{aligned} 2326 \text{ m} = 2326 \text{ m} \cdot \frac{1 \text{ km}}{1000 \text{ m}} ~ & \textcolor{red}{ \text{ Apply conversion factor.}} \\ = 2326 \cancel{ \text{ m}} \cdot \frac{1 \text{ km}}{1000 \cancel{ \text{ m}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{2326 \cdot 1}{1000} \text{ km} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 2.326 \text{ km } & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
In the last step, note that dividing by 1000 moves the decimal point three places to the left. Thus, 2326 meters is equal to 2.326 kilometers.
Alternate Solution
A second solution depends upon the fact that multiplying or dividing by a power of ten will move the decimal point right or left a number of places equal to the number of zeros present in the multiplier or divisor. Thus, as we saw above, dividing by 1000 moved the decimal point 3 places to the left. Suppose that we arrange the metric units of length in order, from largest to smallest, as shown below.

Note that we must move 3 places left to move from the meters (m) abbreviation to the kilometers (km) abbreviation. In like manner, if we write 2,326 meters as 2,326.0meters, then we can convert to kilometers by moving the decimal 3 places to the left.

Change 1,156 meters to kilometers
- Answer
-
1.156 kilometers
Change 537 centimeters to meters.
Solution
We know that
\[1 \text{ cm } = \frac{1}{100} \text{ m,}\nonumber \]
or multiplying both sides of this result by 100,
\[100 \text{ cm } = 1 \text{ m.}\nonumber \]
Dividing both sides of this last result by 100 cm, we obtain the conversion factor 1 m/100 cm.
\[\begin{aligned} 537 \text{ cm } = 537 \text{ cm } \cdot \frac{1 \text{ m}}{100 \text{ cm}} ~ & \textcolor{red}{ \text{ Apply conversion factor.}} \\ = 537 ~ \cancel{ \text{cm}} \cdot \frac{1 \text{ m}}{100 ~ \cancel{ \text{ cm}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{537 \cdot 1}{100} \text{ m} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 5.37 \text{ m} \end{aligned}\nonumber \]
In the last step, note that dividing by 100 moves the decimal point two places to the left. Alternately, we can set up our ordered list of units.

Note that we must move 2 places left to move from the centimeters (cm) abbreviation to the meters (m) abbreviation. In like manner, if we write 537 centimeters as 537.0 centimeters, then we can convert to meters by moving the decimal 2 places to the left.

Sometimes more than one conversion factor is needed.
Change 276 centimeters to meters.
- Answer
-
2.76 meters
Change 10.2 dekameters to centimeters.
Solution
We have two facts:
- 1 dam=10 m, which yields the conversion factor 10 m/1 dam.
- 1 cm=(1/100) m or 100 cm=1 m, which yields the conversion factor 100 cm/1 m.
\[\begin{aligned} 10.2 \text{ dam } = 10.2 \text{ dam } \cdot \frac{10 \text{ m}}{1 \text{ dam}} \cdot \frac{100 \text{ cm}}{1 \text{ m}} ~ & \textcolor{red}{ \text{ Apply conversion factor.}} \\ = 10.2 ~ \cancel{ \text{dam}} \cdot \frac{10 ~ \cancel{ \text{ m}}}{1 ~ \cancel{ \text{ dam}}} \cdot \frac{100 \text{ cm}}{1 ~ \cancel{ \text{ m}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{10.2 \cdot 10 \cdot 100}{1} \text{ cm} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 10,200 \text{ cm} \end{aligned}\nonumber \]
In the last step, note that multiplying by 10, then by 100, moves the decimal point three places to the right.
Alternately, we can set up our ordered list of units.
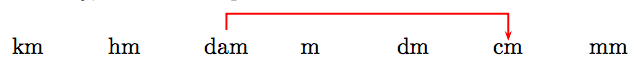
Note that we must move 3 places right to move from the dekameters (dam) abbreviation to the centimeters (cm) abbreviation. In like manner, we can convert 10.2 dekameters to centimeters by moving the decimal 3 places to the right.
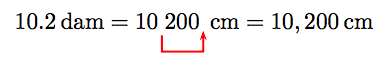
Change 13.5 dekameters to centimeters
- Answer
-
13,500 centimeters
Units of Mass
The fundamental unit of mass in the metric system is called a gram. Originally, it was defined to be equal to one cubic centimeter of water measured at the temperature of melting ice. Now it is simply defined as 1/1000 of a kilogram, which is defined by a physical prototype preserved by the International Bureau of Weights and Measures (Wikipedia). The mass of an object is not the same as an object’s weight, but rather a resistance to motion when an external force is applied.
The same metric system prefixes apply.
These units of mass are used in the metric system.
| Units of Mass | Unit Abbreviation |
| 1 kilogram = 1000 grams | kg |
| 1 hectogram = 100 grams | hg |
| 1 dekagram = 10 grams | dag |
| 1 gram | g |
| 1 decigram = \(\frac{1}{10}\) gram | dg |
| 1 centigram = \(\frac{1}{100}\) gram | cg |
| 1 milligram = \(\frac{1}{1000}\) gram | mg |
Convert 0.025 dekagrams to milligrams.
Solution
We’ll use two conversion factors:
- 1 dag=10 g, which yields the conversion factor 10 g/1 dag.
- 1 mg=(1/1000) g, which yields the conversion factor 1000 mg/1 g.
\[\begin{aligned} 0.025 \text{ dag } = 0.025 \text{ dag } \cdot \frac{10 \text{ g}}{1 \text{ dag}} \cdot \frac{1000 \text{ mg}}{1 \text{ g}} ~ & \textcolor{red}{ \text{ Apply conversion factor.}} \\ = 0.025 ~ \cancel{ \text{dag}} \cdot \frac{10 ~ \cancel{ \text{ g}}}{1 ~ \cancel{ \text{ dag}}} \cdot \frac{1000 \text{ mg}}{1 ~ \cancel{ \text{ g}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{0.025 \cdot 10 \cdot 1000}{1} \text{ mg} ~ & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 250 \text{ mg} \end{aligned}\nonumber \]
Alternately, we can set up our ordered list of units.
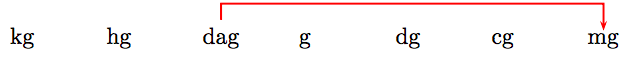
Note that we must move 4 places right to move from the dekagrams (dag) abbreviation to the milligrams (mg) abbreviation. In like manner, we can convert 0.025 dekagrams to milligrams by moving the decimal 4 places to the right.

Convert 0.05 dekagrams to milligrams.
- Answer
-
500 milligrams
Units of Volume
The fundamental unit of volume in the metric system is called a litre. Originally, one litre was defined as the volume of one kilogram of water measured at 4◦ C at 760 millimeters of mercury (Wikipedia). Currently, 1 litre is defined as 1 cubic decimeter (imagine a cube with each edge 1/10 of a meter).
The same metric system prefixes apply.
These units of volume are used in the metric system.
| Unit of Volume | Unit Abbreviation |
| 1 kilolitre = 1000 litres | kL |
| 1 hectolitre = 100 litres | hL |
| 1 dekalitre = 10 litres | daL |
| 1 litre | L |
| 1 decilitre = \(\frac{1}{10}\) litre | dL |
| 1 centilitre = \(\frac{1}{100}\) litre | cL |
| 1 millilitre = \(\frac{1}{1000}\) litre | mL |
Convert 11,725 millilitres to dekalitres.
Solution
We’ll use two conversion factors:
- 1 daL=10 L, which yields the conversion factor 1 daL/10 L.
- 1 mL=(1/1000) L, which yields the conversion factor 1 L/1000 mL.
\[ \begin{aligned} 11, 725 \text{ mL } = 11, 725 \text{ mL } \cdot \frac{1 \text{ L}}{1000 \text{ mL}} \cdot \frac{1 \text{ daL}}{10 \text{ L}} ~ & \textcolor{red}{ \text{ Apply conversion factors.}} \\ = 11, 725 ~ \cancel{\text{mL}} \cdot \frac{1 ~ \cancel{\text{L}}}{1000 ~ \cancel{\text{mL}}} \cdot \frac{1 \text{ daL}}{10 ~ \cancel{\text{L}}} ~ & \textcolor{red}{ \text{ Cancel common units.}} \\ = \frac{11, 725 \cdot 1 \cdot 1}{1000 \cdot 10} \text{ daL } & \textcolor{red}{ \text{ Multiply fractions.}} \\ = 1.1725 \text{ daL} \end{aligned}\nonumber \]
Alternately, we can set up our ordered list of units.
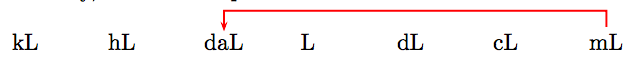
Note that we must move 4 places left to move from the millitres (mL) abbreviation to the dekalitres (daL) abbreviation. In like manner, we can convert 11,725 millilitres to dekalitres by moving the decimal 4 places to the left.
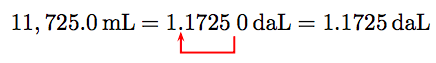
Convert 5,763 millilitres to dekalitres.
- Answer
-
0.5763 dekalitres
Exercises
1. What is the meaning of the metric system prefix centi?
2. What is the meaning of the metric system prefix deka?
3. What is the meaning of the metric system prefix hecto?
4. What is the meaning of the metric system prefix kilo?
5. What is the meaning of the metric system prefix deci?
6. What is the meaning of the metric system prefix milli?
7. What is the meaning of the metric system abbreviation mg?
8. What is the meaning of the metric system abbreviation g?
9. What is the meaning of the metric system abbreviation m?
10. What is the meaning of the metric system abbreviation km?
11. What is the meaning of the metric system abbreviation kL?
12. What is the meaning of the metric system abbreviation daL?
13. What is the meaning of the metric system abbreviation hm?
14. What is the meaning of the metric system abbreviation dm?
15. What is the meaning of the metric system abbreviation dam?
16. What is the meaning of the metric system abbreviation cm?
17. What is the meaning of the metric system abbreviation dL?
18. What is the meaning of the metric system abbreviation L?
19. What is the meaning of the metric system abbreviation hg?
20. What is the meaning of the metric system abbreviation kg?
21. What is the meaning of the metric system abbreviation dg?
22. What is the meaning of the metric system abbreviation dag?
23. What is the meaning of the metric system abbreviation hL?
24. What is the meaning of the metric system abbreviation cL?
25. Change 5,490 millimeters to meters.
26. Change 8,528 millimeters to meters.
27. Change 64 meters to millimeters.
28. Change 65 meters to millimeters.
29. Change 4,571 millimeters to meters.
30. Change 8,209 millimeters to meters.
31. Change 15 meters to centimeters.
32. Change 12 meters to centimeters.
33. Change 569 centimeters to meters.
34. Change 380 centimeters to meters.
35. Change 79 meters to centimeters.
36. Change 60 meters to centimeters.
37. Change 7.6 kilometers to meters.
38. Change 4.9 kilometers to meters.
39. Change 861 centimeters to meters.
40. Change 427 centimeters to meters.
41. Change 4,826 meters to kilometers.
42. Change 1,929 meters to kilometers.
43. Change 4,724 meters to kilometers.
44. Change 1,629 meters to kilometers.
45. Change 6.5 kilometers to meters.
46. Change 7.9 kilometers to meters.
47. Change 17 meters to millimeters.
48. Change 53 meters to millimeters.
49. Change 512 milligrams to centigrams.
50. Change 516 milligrams to centigrams.
51. Change 541 milligrams to centigrams.
52. Change 223 milligrams to centigrams.
53. Change 70 grams to centigrams.
54. Change 76 grams to centigrams.
55. Change 53 centigrams to milligrams.
56. Change 30 centigrams to milligrams.
57. Change 83 kilograms to grams.
58. Change 70 kilograms to grams.
59. Change 8,196 grams to kilograms.
60. Change 6,693 grams to kilograms.
61. Change 564 centigrams to grams.
62. Change 884 centigrams to grams.
63. Change 38 grams to centigrams.
64. Change 88 grams to centigrams.
65. Change 77 centigrams to milligrams.
66. Change 61 centigrams to milligrams.
67. Change 5,337 grams to kilograms.
68. Change 4,002 grams to kilograms.
69. Change 15 kilograms to grams.
70. Change 45 kilograms to grams.
71. Change 833 centigrams to grams.
72. Change 247 centigrams to grams.
73. Change 619,560 centilitres to kilolitres.
74. Change 678,962 centilitres to kilolitres.
75. Change 15.2 litres to millilitres.
76. Change 9.7 litres to millilitres.
77. Change 10,850 centilitres to litres.
78. Change 15,198 centilitres to litres.
79. Change 10.7 litres to millilitres.
80. Change 17.3 litres to millilitres.
81. Change 15,665 millilitres to litres.
82. Change 12,157 millilitres to litres.
83. Change 6.3 kilolitres to centilitres.
84. Change 8.3 kilolitres to centilitres.
85. Change 4.5 kilolitres to centilitres.
86. Change 6.2 kilolitres to centilitres.
87. Change 10.6 litres to centilitres.
88. Change 16.6 litres to centilitres.
89. Change 14,383 centilitres to litres.
90. Change 11,557 centilitres to litres.
91. Change 9.9 litres to centilitres.
92. Change 19.5 litres to centilitres.
93. Change 407,331 centilitres to kilolitres.
94. Change 827,348 centilitres to kilolitres.
95. Change 14,968 millilitres to litres.
96. Change 18,439 millilitres to litres.
Answers
1. 1/100
3. 100
5. 1/10
7. milligram
9. meter
11. kilolitre or kiloliter
13. hectometer
15. dekameter
17. decilitre or deciliter
19. hectogram
21. decigram
23. hectolitre or hectoliter
25. 5.49 meters
27. 64,000 millimeters
29. 4.571 meters
31. 1,500 centimeters
33. 5.69 meters
35. 7,900 centimeters
37. 7,600 meters
39. 8.61 meters
41. 4.826 kilometers
43. 4.724 kilometers
45. 6,500 meters
47. 17,000 millimeters
49. 51.2 centigrams
51. 54.1 centigrams
53. 7,000 centigrams
55. 530 milligrams
57. 83,000 grams
59. 8.196 kilograms
61. 5.64 grams
63. 3,800 centigrams
65. 770 milligrams
67. 5.337 kilograms
69. 15,000 grams
71. 8.33 grams
73. 6.1956 kilolitres
75. 15,200 millilitres
77. 108.5 litres
79. 10,700 millilitres
81. 15.665 litres
83. 630,000 centilitres
85. 450,000 centilitres
87. 1,060 centilitres
89. 143.83 litres
91. 990 centilitres
93. 4.07331 kilolitres
95. 14.968 litres


