11.8: Understand Slope of a Line (Part 2)
- Page ID
- 5044
Graph a Line Given a Point and the Slope
In this chapter, we graphed lines by plotting points, by using intercepts, and by recognizing horizontal and vertical lines.
Another method we can use to graph lines is the point-slope method. Sometimes, we will be given one point and the slope of the line, instead of its equation. When this happens, we use the definition of slope to draw the graph of the line.
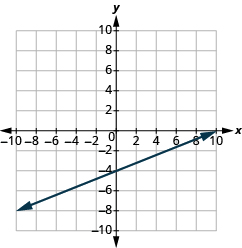
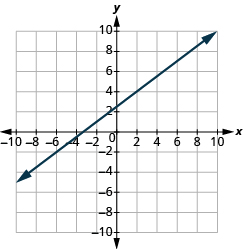
Graph the line passing through the point (1, −1) whose slope is m = \(\dfrac{3}{4}\).
Solution
Plot the given point, (1, −1).
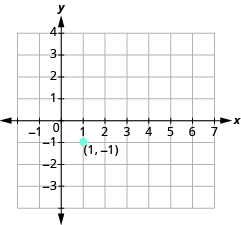
Use the slope formula m = \(\dfrac{rise}{run}\) to identify the rise and the run.
\[\begin{split} m &= \dfrac{3}{4} \\ \dfrac{rise}{run} &= \dfrac{3}{4} \\ rise &= 3 \\ run &= 4 \end{split}\]
Starting at the point we plotted, count out the rise and run to mark the second point. We count 3 units up and 4 units right.
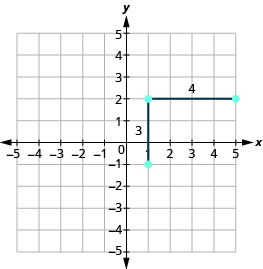
Then we connect the points with a line and draw arrows at the ends to show it continues.
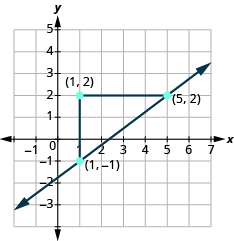
We can check our line by starting at any point and counting up 3 and to the right 4. We should get to another point on the line.
Graph the line passing through the point with the given slope:
(2, −2), m = \(\dfrac{4}{3}\)
- Answer
-
Graph the line passing through the point with the given slope:
(−2, 3), m = \(\dfrac{1}{4}\)
- Answer
-
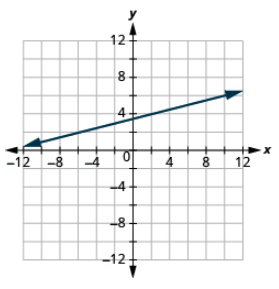
Step 1. Plot the given point.
Step 2. Use the slope formula to identify the rise and the run.
Step 3. Starting at the given point, count out the rise and run to mark the second point.
Step 4. Connect the points with a line.
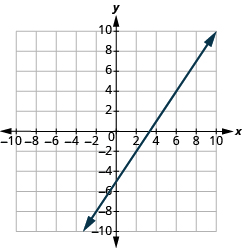
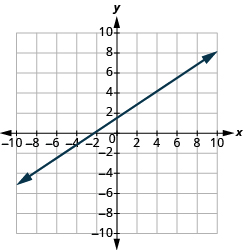
Graph the line with y -intercept (0, 2) and slope m = \(− \dfrac{2}{3}\).
Solution
Plot the given point, the y -intercept (0, 2).
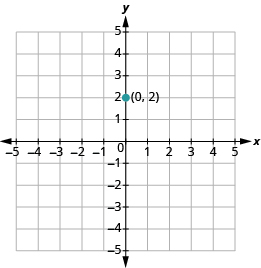
Use the slope formula m = rise run to identify the rise and the run.
\[\begin{split} m &= − \dfrac{2}{3} \\ \dfrac{rise}{run} &= \dfrac{−2}{3} \\ rise &= –2 \\ run &= 3 \end{split}\]
Starting at (0, 2), count the rise and the run and mark the second point.
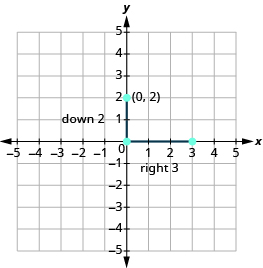
Connect the points with a line.
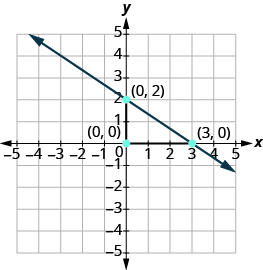
Graph the line with the given intercept and slope:
y-intercept 4, m = \(− \dfrac{5}{2}\)
- Answer
-
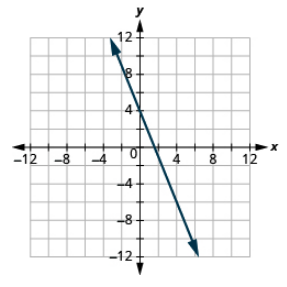
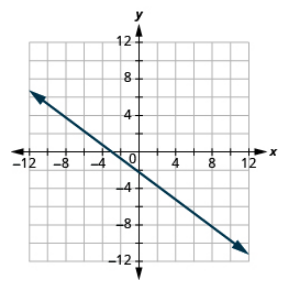
Graph the line with the given intercept and slope:
x-intercept −3, m = \(− \dfrac{3}{4}\)
- Answer
-
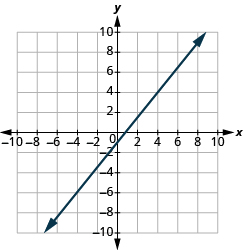
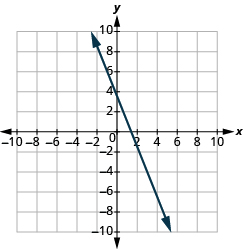
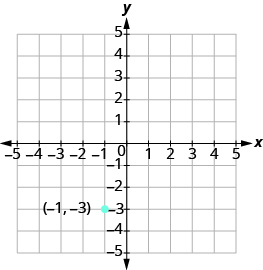
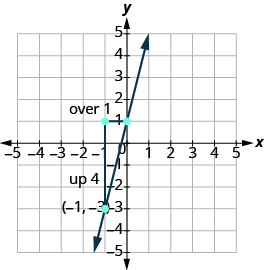
Graph the line passing through the point (−1, −3) whose slope is m = 4.
Solution
Plot the given point.
| Identify the rise and the run. | $$m = 4 \tag{11.4.44}$$ |
| Write 4 as a fraction. | $$\dfrac{rise}{run} = \dfrac{4}{1} \tag{11.4.45}$$ |
| rise = 4, run = 1 |
Count the rise and run.
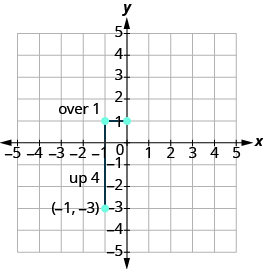
Mark the second point. Connect the two points with a line.
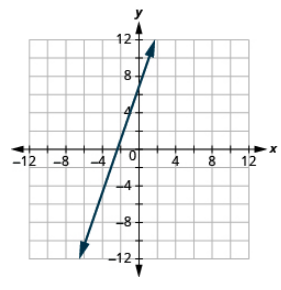
Graph the line with the given intercept and slope: (−2, 1), m = 3.
- Answer
-
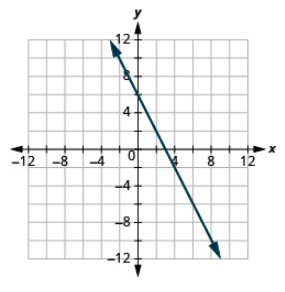
Graph the line with the given intercept and slope: (4, −2), m = −2.
- Answer
-
Solve Slope Applications
At the beginning of this section, we said there are many applications of slope in the real world. Let’s look at a few now.
The pitch of a building’s roof is the slope of the roof. Knowing the pitch is important in climates where there is heavy snowfall. If the roof is too flat, the weight of the snow may cause it to collapse. What is the slope of the roof shown?
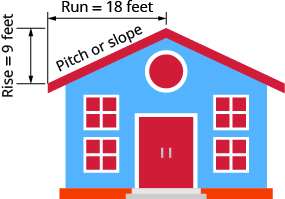
Solution
| Use the slope formula. | $$m = \dfrac{rise}{run} \tag{11.4.46}$$ |
| Substitute the values for rise and run. | $$m = \dfrac{9\; ft}{18\; ft} \tag{11.4.47}$$ |
| Simplify. | $$m = \dfrac{1}{2} \tag{11.4.48}$$ |
| The slope of the roof is \(\dfrac{1}{2}\). |
Find the slope given rise and run: A roof with a rise = 14 and run = 24.
- Answer
-
\(\frac{7}{12}\)
Find the slope given rise and run: A roof with a rise = 15 and run = 36.
- Answer
-
\(\frac{5}{12}\)
Have you ever thought about the sewage pipes going from your house to the street? Their slope is an important factor in how they take waste away from your house.
Sewage pipes must slope down \(\dfrac{1}{4}\) inch per foot in order to drain properly. What is the required slope?

Solution
| Use the slope formula. | $$m = \dfrac{rise}{run} = \dfrac{- \dfrac{1}{4}\; in.}{1\; ft} \tag{11.4.49}$$ |
| Convert 1 foot to 12 inches. | $$m = \dfrac{- \dfrac{1}{4}\; in.}{12\; in} \tag{11.4.50}$$ |
| Simplify. | $$m = - \dfrac{1}{48} \tag{11.4.51}$$ |
| The slope of the pipe is \(− \dfrac{1}{48}\). |
Find the slope of the pipe: The pipe slopes down \(\dfrac{1}{3}\) inch per foot.
- Answer
-
\(-\frac{1}{36}\)
Find the slope of the pipe: The pipe slopes down \(\dfrac{3}{4}\) inch per yard.
- Answer
-
\(-\frac{1}{48}\)
Determine Positive slope from a Graph
Determine Negative slope from a Graph
Determine Slope from Two Points
Practice Makes Perfect
Use Geoboards to Model Slope
In the following exercises, find the slope modeled on each geoboard.
In the following exercises, model each slope. Draw a picture to show your results.
- \(\dfrac{2}{3}\)
- \(\dfrac{3}{4}\)
- \(\dfrac{1}{4}\)
- \(\dfrac{4}{3}\)
- \(- \dfrac{1}{2}\)
- \(- \dfrac{3}{4}\)
- \(- \dfrac{2}{3}\)
- \(- \dfrac{3}{2}\)
Find the Slope of a Line from its Graph
In the following exercises, find the slope of each line shown.
Find the Slope of Horizontal and Vertical Lines
In the following exercises, find the slope of each line.
- y = 3
- y = 1
- x = 4
- x = 2
- y = −2
- y = −3
- x = −5
- x = −4
Use the Slope Formula to find the Slope of a Line between Two Points
In the following exercises, use the slope formula to find the slope of the line between each pair of points.
- (1, 4), (3, 9)
- (2, 3), (5, 7)
- (0, 3), (4, 6)
- (0, 1), (5, 4)
- (2, 5), (4, 0)
- (3, 6), (8, 0)
- (−3, 3), (2, −5)
- (−2, 4), (3, −1)
- (−1, −2), (2, 5)
- (−2, −1), (6, 5)
- (4, −5), (1, −2)
- (3, −6), (2, −2)
Graph a Line Given a Point and the Slope
In the following exercises, graph the line given a point and the slope.
- (1, −2); m = \(\dfrac{3}{4}\)
- (1, −1); m = \(\dfrac{1}{2}\)
- (2, 5); m = \(− \dfrac{1}{3}\)
- (1, 4); m = \(− \dfrac{1}{2}\)
- (−3, 4); m = \(− \dfrac{3}{2}\)
- (−2, 5); m = \(− \dfrac{5}{4}\)
- . (−1, −4); m = \(\dfrac{4}{3}\)
- (−3, −5); m = \(\dfrac{3}{2}\)
- (0, 3); m = \(− \dfrac{2}{5}\)
- (0, 5); m = \(− \dfrac{4}{3}\)
- (−2, 0); m = \(−\dfrac{3}{4}\)
- (−1, 0); m = \(\dfrac{1}{5}\)
- (−3, 3); m = 2
- (−4, 2); m = 4
- (1, 5); m = −3
- (2, 3); m = −1
Solve Slope Applications
In the following exercises, solve these slope applications.
- Slope of a roof A fairly easy way to determine the slope is to take a 12-inch level and set it on one end on the roof surface. Then take a tape measure or ruler, and measure from the other end of the level down to the roof surface. You can use these measurements to calculate the slope of the roof. What is the slope of the roof in this picture?
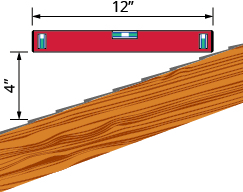
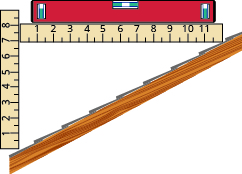
- What is the slope of the roof shown?
- Road grade A local road has a grade of 6%. The grade of a road is its slope expressed as a percent.
- Find the slope of the road as a fraction and then simplify the fraction.
- What rise and run would reflect this slope or grade?
- Highway grade A local road rises 2 feet for every 50 feet of highway.
- What is the slope of the highway?
- The grade of a highway is its slope expressed as a percent. What is the grade of this highway?
Everyday Math
- Wheelchair ramp The rules for wheelchair ramps require a maximum 1 inch rise for a 12 inch run.
- How long must the ramp be to accommodate a 24-inch rise to the door?
- Draw a model of this ramp.
- Wheelchair ramp A 1-inch rise for a 16-inch run makes it easier for the wheelchair rider to ascend the ramp.
- How long must the ramp be to easily accommodate a 24-inch rise to the door?
- Draw a model of this ramp.
Writing Exercises
- What does the sign of the slope tell you about a line?
- How does the graph of a line with slope m = \(\dfrac{1}{2}\) differ from the graph of a line with slope m = 2?
- Why is the slope of a vertical line undefined?
- Explain how you can graph a line given a point and its slope.
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
(b) On a scale of 1–10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."