Skip to main content
Mathematics LibreTexts

11.E: Graphs (Exercises)

  1. Last updated
  2. Save as PDF
  • Page ID
    7296

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    11.1 - Use the Rectangular Coordinate System

    Plot Points in a Rectangular Coordinate System

    In the following exercises, plot each point in a rectangular coordinate system.

    1. (1, 3), (3, 1)
    2. (2, 5), (5, 2)

    In the following exercises, plot each point in a rectangular coordinate system and identify the quadrant in which the point is located.

    1. (a) (−1, −5) (b) (−3, 4) (c) (2, −3) (d) \(\left(1, \dfrac{5}{2}\right)\)
    2. (a) (3, −2) (b) (−4, −1) (c) (−5, 4) (d) \(\left(2, \dfrac{10}{3}\right)\)

    Identify Points on a Graph

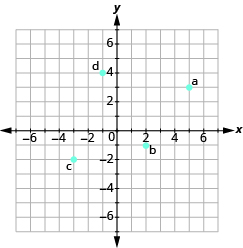
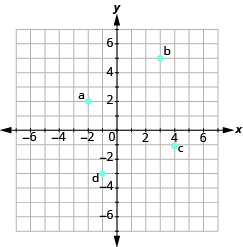
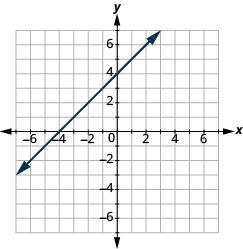
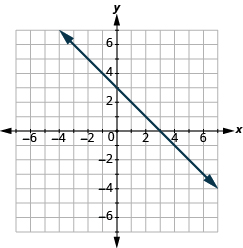
    In the following exercises, name the ordered pair of each point shown in the rectangular coordinate system.

    1. The graph shows the x y-coordinate plane. The axes run from -7 to 7. “a” is plotted at 5, 3, “b” at 2, -1, “c” at -3,-2, and “d” at -1,4.
    2. The graph shows the x y-coordinate plane. The axes run from -7 to 7. “a” is plotted at -2, 2, “b” at 3, 5, “c” at 4,-1, and “d” at -1,3.
    3. The graph shows the x y-coordinate plane. The axes run from -7 to 7. “a” is plotted at 2, 0, “b” at 0, -5, “c” at -4,0, and “d” at 0,3.
    4. The graph shows the x y-coordinate plane. The axes run from -7 to 7. “a” is plotted at 0, 4, “b” at 5, 0, “c” at 0,-1, and “d” at -3,0.

    Verify Solutions to an Equation in Two Variables

    In the following exercises, find the ordered pairs that are solutions to the given equation.

    1. 5x + y = 10
      1. (5, 1)
      2. (2, 0)
      3. (4, −10)
    2. y = 6x − 2
      1. (1, 4)
      2. \(\left(\dfrac{1}{3} , 0\right)\)
      3. (6, −2)

    Complete a Table of Solutions to a Linear Equation in Two Variables

    In the following exercises, complete the table to find solutions to each linear equation.

    1. y = 4x − 1
    x y (x, y)
    0    
    1    
    -2    
    1. y = \(− \dfrac{1}{2}\)x + 3
    x y (x, y)
    0    
    1    
    -2    
    1. x + 2y = 5
    x y (x, y)
      0  
    1    
    -1    
    1. 3x − 2y = 6
    x y (x, y)
    0    
      0  
    -2    

    Find Solutions to a Linear Equation in Two Variables

    In the following exercises, find three solutions to each linear equation.

    1. x + y = 3
    2. x + y = −4
    3. y = 3x + 1
    4. y = − x − 1

    11.2 - Graphing Linear Equations

    Recognize the Relation Between the Solutions of an Equation and its Graph

    In the following exercises, for each ordered pair, decide (a) if the ordered pair is a solution to the equation. (b) if the point is on the line.

    1. y = − x + 4
      1. (0, 4)
      2. (−1, 3)
      3. (2, 2)
      4. (−2, 6)

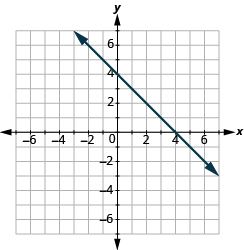
    The graph shows the x y-coordinate plane. The axes run from -7 to 7. A line passes through the points “ordered pair 0, 4” and “ordered pair 4, 0”.

    1. y = \(\dfrac{2}{3}\)x − 1
      1. (0, −1)
      2. (3, 1)
      3. (−3, −3)
      4. (6, 4)

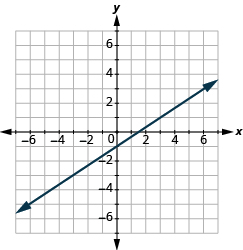
    The graph shows the x y-coordinate plane. The axes run from -7 to 7. A line passes through the points “ordered pair 0, -1” and “ordered pair 3, 1”.

    Graph a Linear Equation by Plotting Points

    In the following exercises, graph by plotting points.

    1. y = 4x − 3
    2. y = −3x
    3. 2x + y = 7

    Graph Vertical and Horizontal lines

    In the following exercises, graph the vertical or horizontal lines.

    1. y = −2
    2. x = 3

    11.3 - Graphing with Intercepts

    Identify the Intercepts on a Graph

    In the following exercises, find the x- and y-intercepts.

    1. The graph shows the x y-coordinate plane. The axes run from -7 to 7. A line passes through the points “ordered pair 0, 4” and “ordered pair -4, 0”.
    2. The graph shows the x y-coordinate plane. The x-axis runs from -1 to 6. The y-axis runs from -4 to 2. A line passes through the points “ordered pair 5, 1” and “ordered pair 0, -3”.

    Find the Intercepts from an Equation of a Line

    In the following exercises, find the intercepts.

    1. x + y = 5
    2. x − y = −1
    3. y = \(\dfrac{3}{4}\)x − 12
    4. y = 3x

    Graph a Line Using the Intercepts

    In the following exercises, graph using the intercepts.

    1. −x + 3y = 3
    2. x + y = −2

    Choose the Most Convenient Method to Graph a Line

    In the following exercises, identify the most convenient method to graph each line.

    1. x = 5
    2. y = −3
    3. 2x + y = 5
    4. x − y = 2
    5. y = \(\dfrac{1}{2}\)x + 2
    6. y = \(\dfrac{3}{4}\)x − 1

    11.4 - Understand Slope of a Line

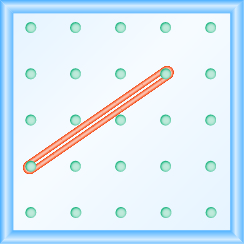
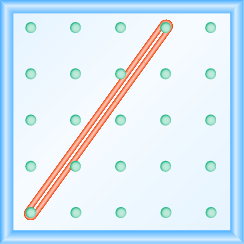
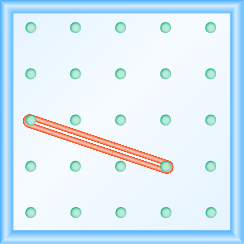
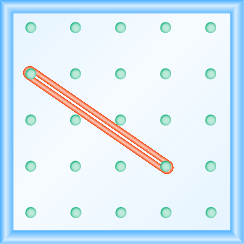
    Use Geoboards to Model Slope

    In the following exercises, find the slope modeled on each geoboard.

    1. The figure shows a grid of evenly spaced dots. There are 5 rows and 5 columns. There is a rubber band style loop connecting the point in column 1 row 4 and the point in column 4 row 2.
    2. The figure shows a grid of evenly spaced dots. There are 5 rows and 5 columns. There is a rubber band style loop connecting the point in column 1 row 5 and the point in column 4 row 1.
    3. The figure shows a grid of evenly spaced dots. There are 5 rows and 5 columns. There is a rubber band style loop connecting the point in column 1 row 3 and the point in column 4 row 4.
    4. The figure shows a grid of evenly spaced dots. There are 5 rows and 5 columns. There is a rubber band style loop connecting the point in column 1 row 2 and the point in column 4 row 4.

    In the following exercises, model each slope. Draw a picture to show your results.

    1. \(\dfrac{1}{3}\)
    2. \(\dfrac{3}{2}\)
    3. \(− \dfrac{2}{3}\)
    4. \(− \dfrac{1}{2}\)

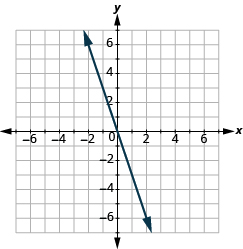
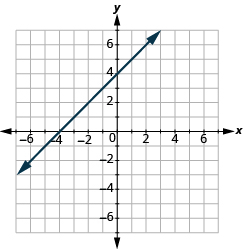
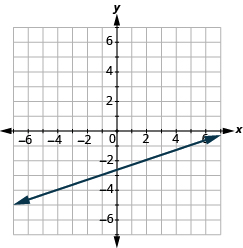
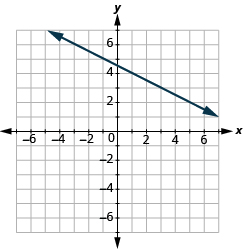
    Find the Slope of a Line from its Graph

    In the following exercises, find the slope of each line shown.

    1. The graph shows the x y-coordinate plane. The axes run from -7 to 7. A line passes through the points “ordered pair 0, 0” and “ordered pair 2, -6”.
    2. The graph shows the x y-coordinate plane. The axes run from -7 to 7. A line passes through the points “ordered pair 0, 4” and “ordered pair -4, 0”.
    3. The graph shows the x y-coordinate plane. The axes run from -7 to 7. A line passes through the points “ordered pair -4, -4” and “ordered pair 5, -1”.
    4. The graph shows the x y-coordinate plane. The axes run from -7 to 7. A line passes through the points “ordered pair -3, 6” and “ordered pair 5, 2”.

    Find the Slope of Horizontal and Vertical Lines

    In the following exercises, find the slope of each line.

    1. y = 2
    2. x = 5
    3. x = −3
    4. y = −1

    Use the Slope Formula to find the Slope of a Line between Two Points

    In the following exercises, use the slope formula to find the slope of the line between each pair of points.

    1. (2, 1), (4, 5)
    2. (−1, −1), (0, −5)
    3. (3, 5), (4, −1)
    4. (−5, −2), (3, 2)

    Graph a Line Given a Point and the Slope

    In the following exercises, graph the line given a point and the slope.

    1. (2, −2); m = \(\dfrac{5}{2}\)
    2. (−3, 4); m = \(− \dfrac{1}{3}\)

    Solve Slope Applications

    In the following exercise, solve the slope application.

    1. A roof has rise 10 feet and run 15 feet. What is its slope?

    PRACTICE TEST

    1. Plot and label these points:
      1. (2, 5)
      2. (−1, −3)
      3. (−4, 0)
      4. (3, −5)
      5. (−2, 1)
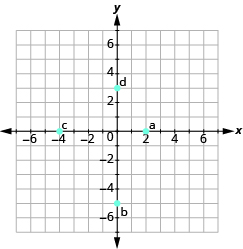
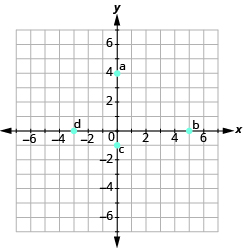
    2. Name the ordered pair for each point shown.

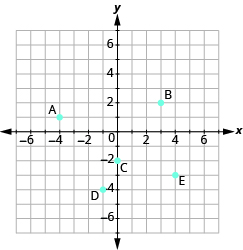
    The graph shows the x y-coordinate plane. The axes extend from -7 to 7. A is plotted at -4, 1, B at 3, 2, C at 0, -2, D at -1, -4, and E at 4,-3.

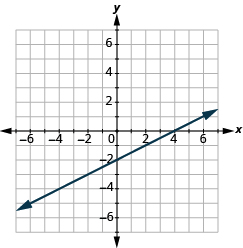
    1. Find the x-intercept and y-intercept on the line shown.

    The graph shows the x y-coordinate plane. The x-axis runs from -7 to 7. The y-axis runs from -7 to 7. A line passes through the points “ordered pair 4, 0” and “ordered pair 0, -2”.

    1. Find the x-intercept and y-intercept of the equation 3x − y = 6.
    2. Is (1, 3) a solution to the equation x + 4y = 12? How do you know?
    3. Complete the table to find four solutions to the equation y = − x + 1.
    x y (x, y)
    0    
    1    
    3    
    -2    
    1. Complete the table to find three solutions to the equation 4x + y = 8.
    x y (x, y)
    0    
      0  
    3    

    In the following exercises, find three solutions to each equation and then graph each line.

    1. y = −3x
    2. 2x + 3y = −6

    In the following exercises, find the slope of each line.

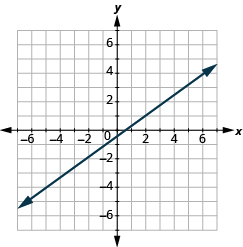
    1. The graph shows the x y-coordinate plane. The axes run from -7 to 7. The y-axis runs from -5 to -4. A line passes through the points “ordered pair 6, 4” and “ordered pair 0, -3”.
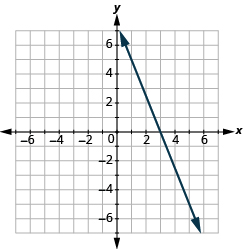
    2. The graph shows the x y-coordinate plane. The axes run from -7 to 7. A line passes through the points “ordered pair 3, 0” and “ordered pair 1, 5”.
    3. Use the slope formula to find the slope of the line between (0, −4) and (5, 2).
    4. Find the slope of the line y = 2.
    5. Graph the line passing through (1, 1) with slope m = \(\dfrac{3}{2}\).
    6. A bicycle route climbs 20 feet for 1,000 feet of horizontal distance. What is the slope of the route?

    Contributors and Attributions

    11.E: Graphs (Exercises) is shared under a CC BY license and was authored, remixed, and/or curated by LibreTexts.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      License
      CC BY
      Show Page TOC
      no
    2. Tags
      This page has no tags.