9.4: Perimeter and Circumference of Geometric Figures

Last updated
Save as PDF

Page ID: 48888

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

know what a polygon is
know what perimeter is and how to find it
know what the circumference, diameter, and radius of a circle is and how to find each one
know the meaning of the symbol ππ and its approximating value
know what a formula is and four versions of the circumference formula of a circle

Polygons

We can make use of conversion skills with denominate numbers to make measurements of geometric figures such as rectangles, triangles, and circles. To make these measurements we need to be familiar with several definitions.

Definition: Polygon

A polygon is a closed plane (flat) figure whose sides are line segments (portions of straight lines).

Polygons

$Four shapes, each completely closed, with various numbers of straight line segments as sides.$ $graphics2.png$ $graphics3.png$ $graphics4.png$

Not polygons

$Four shapes. One three-sided open box. One oval. One oval-shaped object with one flat side, and one nondescript blob.$ $graphics6.png$ $graphics7.png$ $graphics8.png$

Perimeter

Definition: Perimeter

The perimeter of a polygon is the distance around the polygon.

To find the perimeter of a polygon, we simply add up the lengths of all the sides.

Sample Set A

Find the perimeter of each polygon.

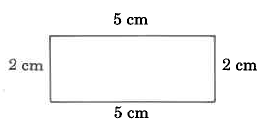
$A rectangle with short sides of length 2 cm and long sides of length 5 cm.$

Solution

$\begin{array} {rcl} {\text{Perimeter}} & = & {\text{2 cm + 5 cm + 2 cm + 5 cm}} \\ {} & = & {\text{14 cm}} \end{array}$

Sample Set A

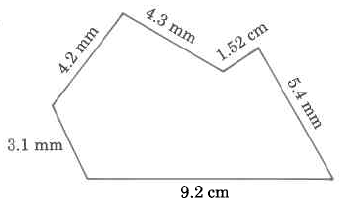
$A polygon with sides of the following lengths: 9.2cm, 31mm, 4.2mm, 4.3mm, 1.52cm, and 5.4mm.$

Solution

$\begin{array} {rcr} {\text{Perimeter}} & = & {\text{3.1 mm}} \\ {} & & {\text{4.2 mm}} \\ {} & & {\text{4.3 mm}} \\ {} & & {\text{1.52 mm}} \\ {} & & {\text{5.4 mm}} \\ {} & & {\underline{\text{+ 9.2 mm}}} \\ {} & & {\text{27.72 mm}} \end{array}$

Sample Set A

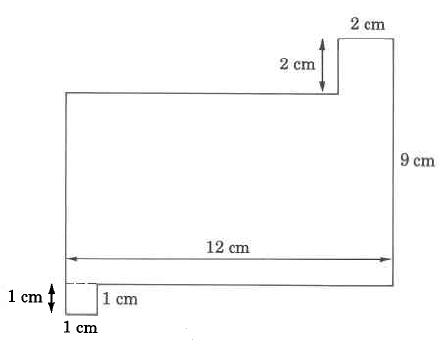
$A polygon with eight sides. It is not an octagon, but can be visualized as one large rectangle with two smaller rectangles connected to it.$

Solution

Our first observation is that three of the dimensions are missing. However, we can determine the missing measurements using the following process. Let A, B, and C represent the missing measurements. Visualize

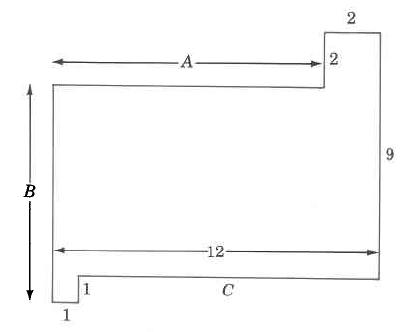
$A polygon with eight sides. It is not an octagon, but can be visualized as one large rectangle with two smaller rectangles connected to it. The height and width are measured and labeled with variables, A, B, and C.$

$\text{A = 12m - 2m = 10m}$
$\text{B = 9m + 1m - 2m = 8m}$
$\text{C = 12m - 1m = 11m}$

$\begin{array} {rcr} {\text{Perimeter}} & = & {\text{8 m}} \\ {} & & {\text{10 m}} \\ {} & & {\text{2 m}} \\ {} & & {\text{2 m}} \\ {} & & {\text{9 m}} \\ {} & & {\text{11 m}} \\ {} & & {\text{1 m}} \\ {} & & {\underline{\text{+ 1 m}}} \\ {} & & {\text{44 m}} \end{array}$

Practice Set A

Find the perimeter of each polygon.

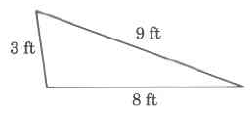
$A three-sided polygon with sides of the following lengths: 3 ft, 8 ft, and 9 ft.$

Answer: 20 ft

Practice Set A

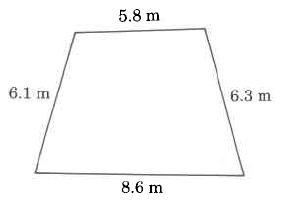
$A four-sided polygon with sides of the following length: 6.1m, 8.6m, 6.3m, and 5.8m.$

Answer: 26.8 m

Practice Set A

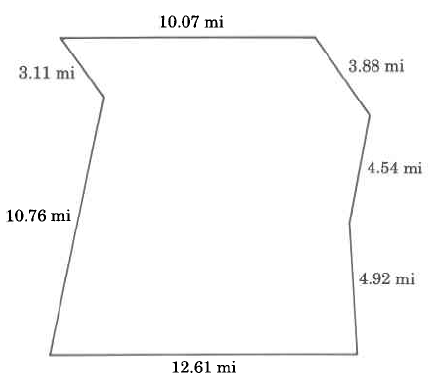
$A seven-sided polygon with sides of the following lengths: 10.07mi, 3.88mi, 4.54mi, 4.92mi, 12.61, 10.76mi, and 3.11mi.$

Answer: 49.89 mi

Circumference/Diameter/Radius

Circumference
The circumference of a circle is the distance around the circle.

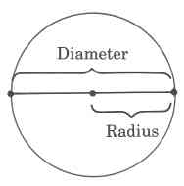
Diameter
A diameter of a circle is any line segment that passes through the center of the circle and has its endpoints on the circle.

Radius
A radius of a circle is any line segment having as its endpoints the center of the circle and a point on the circle.
The radius is one half the diameter.

$A circle with a line directly through the middle, ending at the edges of the shape. The entire length of the line is labeled diameter, and the length of the portion of the line from the center of the circle to the edge of the circle is labeled radius.$

The Number $\pi$

The symbol $\pi$, read "pi," represents the nonterminating, nonrepeating decimal number 3.14159 … . This number has been computed to millions of decimal places without the appearance of a repeating block of digits.

For computational purposes, $\pi$ is often approximated as 3.14. We will write $\pi \approx 3.14$ to denote that $\pi$ is approximately equal to 3.14. The symbol "≈" means "approximately equal to."

Formulas

To find the circumference of a circle, we need only know its diameter or radius. We then use a formula for computing the circumference of the circle.

Formula
A formula is a rule or method for performing a task. In mathematics, a formula is a rule that directs us in computations.

Formulas are usually composed of letters that represent important, but possibly unknown, quantities.

If $C, d$, and $r$ represent, respectively, the circumference, diameter, and radius of a circle, then the following two formulas give us directions for computing the circumference of the circle.

Circumference Formulas

$C = \pi d$ or $C \approx (3.14) d$
$C = 2 \pi r$ or $C \approx 2 (3.14) r$

Sample Set B

Find the exact circumference of the circle.

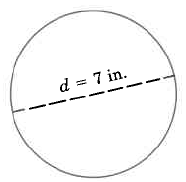
$A circle with a dashed line from one edge to the other, labeled d = 7 in.$

Solution

Use the formula $C = \pi d$.

$C = \pi \cdot 7\ in.$

By commutativity of multiplication,

$C = 7\ in. \cdot \pi$

$C = 7 \pi in.$, exactly

This result is exact since $\pi$ has not been approximated.

Sample Set B

Find the approximate circumference of the circle.

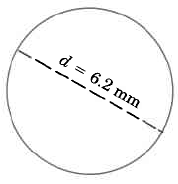
$A circle with a dashed line from one edge to the other, labeled d = 6.2 mm.$

Solution

Use the formula $C = \pi d$.

$C \approx (3.14)(6.2)$

$C \approx 19.648 \text{ mm}$

This result is approximate since ππ has been approximated by 3.14.

Sample Set B

Find the approximate circumference of a circle with radius 18 inches.

Solution

Since we're given that the radius, $r$, is 18 in., we'll use the formula $C = 2\pi r$.

$C \approx (2)(3.14)(18 \text{ in.})$

$C \approx 113.04 \text{ in.}$

Sample Set B

Find the approximate perimeter of the figure.

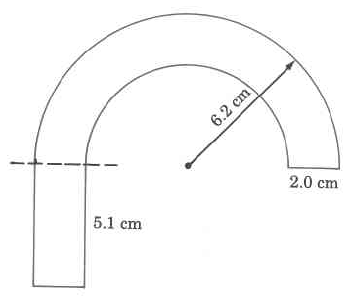
$A cane-shaped object of an even thickness, with one straight portion and one portion shaped in a half-circle. The thickness is 2.0cm, the length of the straight portion is 5.1cm, and the radius of the semicircle portion is 6.2cm.$

Solution

We notice that we have two semicircles (half circles).

The larger radius is 6.2 cm.

The smaller radius is $\text{6.2 cm - 2.0 cm = 4.2 cm.}$

The width of the bottom part of the rectangle is 2.0 cm.

$\begin{array} {rcll} {\text{Perimeter}} & = & {\text{2.0 cm}} & {} \\ {} & & {\text{5.1 cm}} & {} \\ {} & & {\text{2.0 cm}} & {} \\ {} & & {\text{5.1 cm}} & {} \\ {} & & {(0.5) \cdot (2) \cdot (3.14) \cdot \text{(6.2 com)}} & {\text{Circumference of outer semicircle.}} \\ {} & \ \ + & {\underline{(0.5) \cdot (2) \cdot (3.14) \cdot \text{(4.2 com)}}} & {\text{Circumference of inner semicircle.}} \\ {} & & {} & {\text{6.2 cm - 2.0 cm = 4.2 cm}} \\ {} & & {} & {\text{The 0.5 appears because we want the}} \\ {} & & {} & {\text{perimeter of only half a circle.}} \end{array}$

$\begin{array} {rcr} {\text{Perimeter}} & \approx & {\text{2.0 cm}} \\ {} & & {\text{5.1 cm}} \\ {} & & {\text{2.0 cm}} \\ {} & & {\text{5.1 cm}} \\ {} & & {\text{19.468 cm}} \\ {} & & {\underline{\text{+13.188 cm}}} \\ {} & & {\text{48.856 cm}} \end{array}$

Practice Set B

Find the exact circumference of the circle.

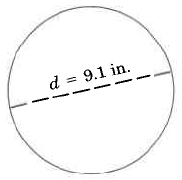
$A circle with a line through the middle, ending at the edges of the circle. The line is labeled, d = 9.1in.$

Answer: $9.1 \pi$ in.

Practice Set B

Find the approximate circumference of the circle.

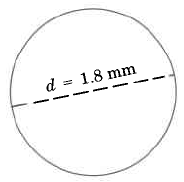
$A circle with a line through the middle, ending at the edges of the circle. The line is labeled, d = 1.8in.$

Answer: 5.652 mm

Practice Set B

Find the approximate circumference of the circle with radius 20.1 m.

Answer: 126.228 m

Practice Set B

Find the approximate outside perimeter of

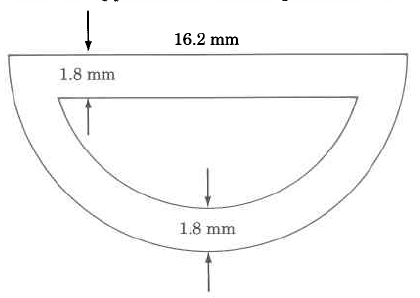
$A shape best visualized as a hollow half-circle. The thickness is 1.8mm, and the diameter of the widest portion of the half-circle is 16.2mm.$

Answer: 41.634 mm

Exercises

Find each perimeter or approximate circumference. Use $\pi = 3.14$.

Exercise $\PageIndex{1}$

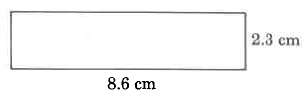
$A rectangle with sides of length 2.3cm and 8.6cm.$

Answer: 21.8 cm

Exercise $\PageIndex{2}$

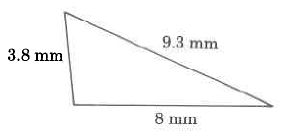
$A triangle with sides of length 8mm, 9.3mm, and 3.8mm.$

Exercise $\PageIndex{3}$

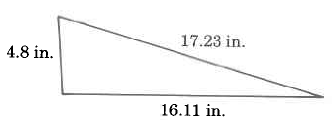
$A triangle with sides of length 4.8in, 16.11in, and 17.23in.$

Answer: 38.14 inches

Exercise $\PageIndex{4}$

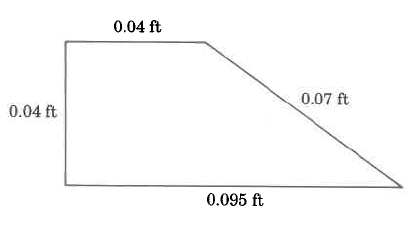
$A four-sided polygon with sides of length 0.04ft, 0.07ft, 0.04ft, and 0.095ft.$

Exercise $\PageIndex{5}$

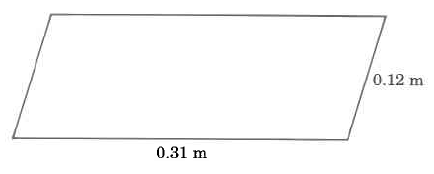
$A four sided parallelogram with short sides of length 0.12m and long sides of length 0.31m.$

Answer: 0.86 m

Exercise $\PageIndex{6}$

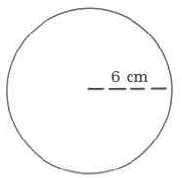
$A circle of radius 6m.$

Exercise $\PageIndex{7}$

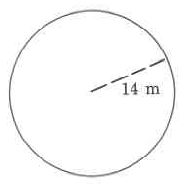
$A circle of radius 14m.$

Answer: 87.92 m

Exercise $\PageIndex{8}$

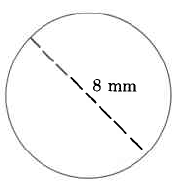
$A circle of diameter 8mm.$

Exercise $\PageIndex{9}$

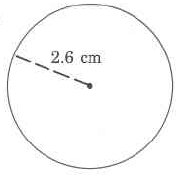
$A circle of diameter 2.6cm.$

Answer: 16.328 cm

Exercise $\PageIndex{10}$

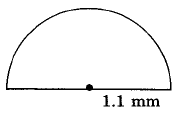
$A half-circle of diameter 1.1mm.$

Exercise $\PageIndex{11}$

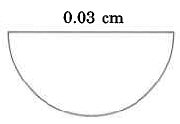
$A half-circle of diameter 0.03cm.$

Answer: 0.0771 cm

Exercise $\PageIndex{12}$

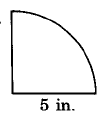
$A quarter-circle of radius 5 in.$

Exercise $\PageIndex{13}$

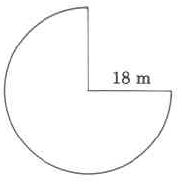
$Three quarters of a circle. The radius is 18m.$

Answer: 120.78 m

Exercise $\PageIndex{14}$

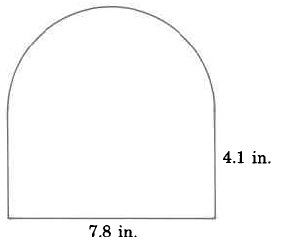
$A shape best visualized as a rectangle connected to a half-circle on top. The rectangle's height is 4.1in, and the rectangle's width is 7.8in.$

Exercise $\PageIndex{15}$

$A shape best visualized as a rectangle connected to a half-circle on top. The rectangle's height is 4.1in, and the rectangle's width is 7.8in.$

Answer: 21.71 inches

Exercise $\PageIndex{16}$

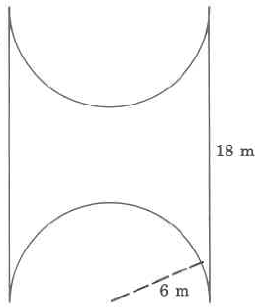
$A shape best described as a rectangle with two half-circle slices taken out of the top and bottom. The rectangle's height is 18m, and the radius of the circles is 6m.$

Exercise $\PageIndex{17}$

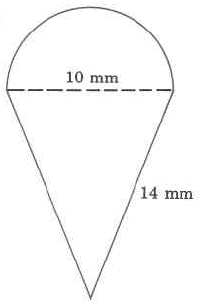
$A shape best described as an ice cream cone, or a triangle with a half-circle attached to the top. The sides of the triangle are measured to be 14mm, and the diameter of the half-circle is 10mm.$

Answer: 43.7 mm

Exercise $\PageIndex{18}$

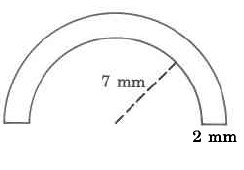
$A tube in the shape of a half-circle with straight ends. The ends have a width of 2mm, and the inner side of the circular tube has a radius of 7mm.$

Exercise $\PageIndex{19}$

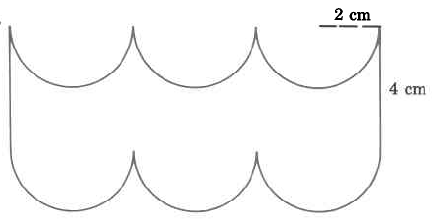
$A rectangle that has three half-circular cutouts and three half-circular additions. The vertical straight edge is length 4cm, and the radius of the circular cutouts and additions are 2cm.$

Answer: 45.68 cm

Exercise $\PageIndex{20}$

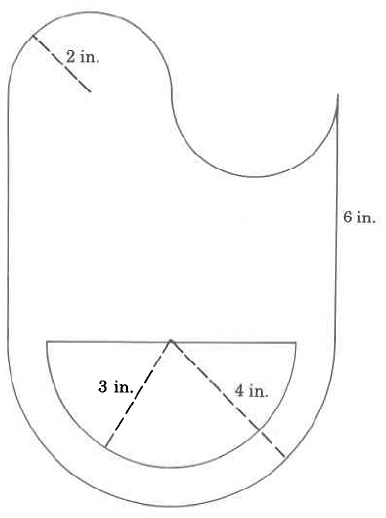
$A complex shape.$

Exercises for Review

Exercise $\PageIndex{19}$

Find the value of $2 \dfrac{8}{13} \cdot \sqrt{10 \dfrac{9}{16}}$.

Answer: 8.5 or $\dfrac{17}{2}$ or $8 \dfrac{1}{2}$

Exercise $\PageIndex{20}$

Find the value of $\dfrac{8}{15} + \dfrac{7}{10} + \dfrac{21}{60}$.

Exercise $\PageIndex{19}$

Convert $\dfrac{7}{8}$ to a decimal.

Answer: 0.875

Exercise $\PageIndex{20}$

What is the name given to a quantity that is used as a comparison to determine the measure of another quantity?

Exercise $\PageIndex{19}$

Add 42 min 26 sec to 53 min 40 sec and simplify the result.

Answer: 1 hour 36 minutes 6 seconds

Polygons

Perimeter

Circumference/Diameter/Radius

The Number \(\pi\)

Formulas

Exercises

Exercises for Review