10.1: Variables, Constants, and Real Numbers

Learning Objectives

• be able to distinguish between variables and constants
• be able to recognize a real number and particular subsets of the real numbers
• understand the ordering of the real numbers

Variables and Constants

A basic distinction between algebra and arithmetic is the use of symbols (usually letters) in algebra to represent numbers. So, algebra is a generalization of arithme­tic. Let us look at two examples of situations in which letters are substituted for numbers:

1. Suppose that a student is taking four college classes, and each class can have at most 1 exam per week. In any 1-week period, the student may have 0, 1, 2, 3, or 4 exams. In algebra, we can let the letter \(x\) represent the number of exams this student may have in a 1-week period. The letter \(x\) may assume any of the various values 0, 1, 2, 3, 4.
2. Suppose that in writing a term paper for a biology class a student needs to specify the average lifetime, in days, of a male housefly. If she does not know this number off the top of her head, she might represent it (at least temporarily) on her paper with the letter \(t\) (which reminds her of time). Later, she could look up the average time in a reference book and find it to be 17 days. The letter \(t\) can assume only the one value, 17, and no other values. The value \(t\) is constant.

Definition: Variable, Constant

1. A letter or symbol that represents any member of a collection of two or more numbers is called a variable.
2. A letter or symbol that represents one specific number, known or unknown, is called a constant.

In example 1, the letter \(x\) is a variable since it can represent any of the numbers 0, 1, 2, 3, 4. The letter \(t\) example 2 is a constant since it can only have the value 17.

Real Numbers

Real Number Line
The study of mathematics requires the use of several collections of numbers. The real number line allows us to visually display (graph) the numbers in which we are interested.

A line is composed of infinitely many points. To each point we can associate a unique number, and with each number, we can associate a particular point.

Definition: Coordinate

The number associated with a point on the number line is called the coordinate of the point.

Definition: Graph

The point on a number line that is associated with a particular number is called the graph of that number.

Constructing a Real Number Line
We construct a real number line as follows:

Draw a horizontal line.

Origin
Choose any point on the line and label it 0. This point is called the origin.

Choose a convenient length. Starting at 0, mark this length off in both direc­tions, being careful to have the lengths look like they are about the same.

We now define a real number.

Definition: Real Number

A real number is any number that is the coordinate of a point on the real number line.

Definition: Positive Number, Negative Numbers

Real numbers whose graphs are to the right of 0 are called positive real numbers, or more simply, positive numbers. Real numbers whose graphs appear to the left of 0 are called negative real numbers, or more simply, negative numbers.

The number 0 is neither positive nor negative.

Subsets of Real Numbers

The set of real numbers has many subsets. Some of the subsets that are of interest in the study of algebra are listed below along with their notations and graphs.

Natural Numbers, Counting Numbers
The natural or counting numbers \((N)\): 1, 2, 3, 4, . . . Read “and so on.”

Whole Numbers
The whole numbers \((W)\): 0, 1, 2, 3, 4, . . .

Notice that every natural number is a whole number.

Integers
The integers \((Z)\): . . . -3, -2, -1, 0, 1, 2, 3, . . .

Notice that every whole number is an integer.

Rational Numbers (Fractions)
The rational numbers \((Q)\): Rational numbers are sometimes called fractions. They are numbers that can be written as the quotient of two integers. They have decimal representations that either terminate or do not terminate but contain a repeating block of digits. Some examples are
\(\underbrace{\dfrac{-3}{4} = -0.75}_{text{Terminating}}\) \(\underbrace{8 \dfrac{11}{27} = 8.407407407...}_{\text{Nonterminating, but repeating.}}\)

Some rational numbers are graphed below.

Notice that every integer is a rational number.

Notice that there are still a great many points on the number line that have not yet been assigned a type of number. We will not examine these other types of numbers in this text. They are examined in detail in algebra. An example of these numbers is the number \(\pi\), whose decimal representation does not terminate nor contain a repeating block of digits. An approximation for \(\pi\) is 3.14.

Sample Set A

Is every whole number a natural number?

Solution

No. The number 0 is a whole number but it is not a natural number.

Sample Set A

Is there an integer that is not a natural number?

Solution

Yes. Some examples are 0, -1, -2, -3, and -4.

Sample Set A

Is there an integer that is a whole number?

Solution

Yes. In fact, every whole number is an integer.

Practice Set A

Is every natural number a whole number?

Answer

yes

Practice Set A

Is every whole number an integer?

Answer

yes

Practice Set A

Is every integer a real number?

Answer

yes

Practice Set A

Is there an integer that is a whole number?

Answer

yes

Practice Set A

Is there an integer that is not a natural number?

Answer

yes

Ordering Real Numbers

Ordering Real Numbers
A real number \(b\) is said to be greater than a real number \(a\), denoted \(b > a\), if \(b\) is to the right of \(a\) on the number line. Thus, as we would expect, \(5 > 2\) since 5 is to the right of 2 on the number line. Also, \(-2 > -5\) since -2 is to the right of -5 on the number line.

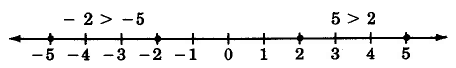
If we let \(a\) and \(b\) represent two numbers, then \(a\) and \(b\) are related in exactly one of three ways: Either

Equality Symbol
\(a = b\) \(a\) and \(b\) are equal (8 = 8)

Inequality Symbols
\(\begin{cases} a > b & a \text{ is greater than }b & (8 > 5) \\ a < b & a \text{ is less than } b & (5 < 8) \\ \ & \text{Some variations of these symbols are} & \ \\ a \ne b & a \text{ is not equal to } b & (8 \ne 5) \\ a \ge b & a \text{ is greater than or equal to } b & (a \ge 8) \\ a \le b & a \text{ is less than or equal to } b & (a \le 8) \end{cases}\)

Sample Set B

What integers can replace xx so that the following statement is true?

\(-3 \le x < 2\)

Solution

The integers are -3, -2, -1, 0, 1.

Sample Set B

Draw a number line that extends from -3 to 5. Place points at all whole numbers between and including -1 and 3.

Solution

-1 is not a whole number

Practice Set B

What integers can replace \(x\) so that the following statement is true? \(-5 \le x < 2\)

Answer

-5, -4, -3, -2, -1, 0

Practice Set B

Draw a number line that extends from -4 to 3. Place points at all natural numbers between, but not including, -2 to 2.

Answer

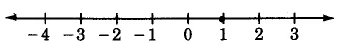
Exercises

For the following 8problems, next to each real number, note all collections to which it belongs by writing \(N\) for natural number, \(W\) for whole number, or \(Z\) for integer. Some numbers may belong to more than one collec­tion.

Exercise \(\PageIndex{1}\)

6

Answer

N, W, Z

Exercise \(\PageIndex{2}\)

12

Exercise \(\PageIndex{3}\)

0

Answer

W, Z

Exercise \(\PageIndex{4}\)

1

Exercise \(\PageIndex{5}\)

-3

Answer

Z

Exercise \(\PageIndex{6}\)

-7

Exercise \(\PageIndex{7}\)

-805

Answer

Z

Exercise \(\PageIndex{8}\)

-900

Exercise \(\PageIndex{9}\)

Is the number 0 a positive number, a negative number, neither, or both?

Answer

Neither

Exercise \(\PageIndex{10}\)

An integer is an even integer if it is evenly divisi­ble by 2. Draw a number line that extends from -5 to 5 and place points at all negative even integers and all positive odd integers.

Exercise \(\PageIndex{11}\)

Draw a number line that extends from -5 to 5. Place points at all integers that satisfy \(-3 \le x < 4\).

Answer

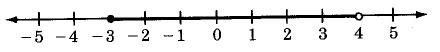
Exercise \(\PageIndex{12}\)

Is there a largest two digit number? If so, what is it?

Exercise \(\PageIndex{13}\)

Is there a smallest two digit number? If so, what is it?

Answer

Yes, 10

For the pairs of real numbers in the following 5 problems, write the appropriate symbol (<, >, =) in place of the □.

Exercise \(\PageIndex{14}\)

-7 □ -2

Exercise \(\PageIndex{15}\)

-5 □ 0

Answer

<

Exercise \(\PageIndex{16}\)

-1 □ 4

Exercise \(\PageIndex{17}\)

6 □ -1

Answer

>

Exercise \(\PageIndex{18}\)

10 □ 10

For the following 5 problems, what numbers can replace m so that the following statements are true?

Exercise \(\PageIndex{19}\)

\(-1 \le m \le -5\), \(m\) an integer.

Answer

{-1, 0, 1, 2, 3, 4, 5}

Exercise \(\PageIndex{20}\)

\(-7 < m < -1\), \(m\) an integer.

Exercise \(\PageIndex{21}\)

\(-3 \le m < 2\), \(m\) a natural number.

Answer

{1}

Exercise \(\PageIndex{22}\)

\(-15 < m \le -1\), \(m\) a natural number.

Exercise \(\PageIndex{23}\)

\(-5 \le m < 5\), \(m\) a whole number.

Answer

{0, 1, 2, 3, 4}

For the following 10 problems, on the number line, how many units are there between the given pair of numbers?

Exercise \(\PageIndex{24}\)

0 and 3

Exercise \(\PageIndex{25}\)

-4 and 0

Answer

4

Exercise \(\PageIndex{26}\)

-1 and 6

Exercise \(\PageIndex{27}\)

-6 and 2

Answer

8

Exercise \(\PageIndex{28}\)

-3 and 3

Exercise \(\PageIndex{29}\)

Are all positive numbers greater than zero?

Answer

yes

Exercise \(\PageIndex{30}\)

Are all positive numbers greater than all nega­tive numbers?

Exercise \(\PageIndex{31}\)

Is 0 greater than all negative number?

Answer

yes

Exercise \(\PageIndex{32}\)

Is there a largest natural number?

Exercise \(\PageIndex{33}\)

Is there a largest negative integer?

Answer

yes, -1

Exercises for Review

Exercise \(\PageIndex{34}\)

Convert \(6 \dfrac{5}{8}\) to an improper fraction.

Exercise \(\PageIndex{35}\)

Find the value: \(\dfrac{3}{11}\) of \(\dfrac{33}{5}\).

Answer

\(\dfrac{9}{5}\) or \(1 \dfrac{4}{5}\) or 1.8

Exercise \(\PageIndex{36}\)

Find the sum of \(\dfrac{4}{5} + \dfrac{3}{8}\).

Exercise \(\PageIndex{37}\)

Convert 30.06 cm to m.

Answer

0.3006 m

Exercise \(\PageIndex{38}\)

Find the area of the triangle.