2.2.4: Side Length Quotients in Similar Triangles

Lesson

Let's find missing side lengths in triangles.

Exercise \(\PageIndex{1}\): Two-three-four and Four-five-six

Triangle \(A\) has side lengths 2, 3, and 4. Triangle \(B\) has side lengths 4, 5, and 6. Is Triangle \(A\) similar to Triangle \(B\)?

Exercise \(\PageIndex{2}\): Quotients of Sides Within Similar Triangles

Triangle \(ABC\) is similar to triangles \(DEF\), \(GHI\), and \(JKL\). The scale factors for the dilations that show triangle \(ABC\) is similar to each triangle are in the table.

Figure \(\PageIndex{1}\)

1. Find the side lengths of triangles \(DEF\), \(GHI\), and \(JKL\). Record them in the table.

Table \(\PageIndex{1}\)

triangle	scale factor	length of short side	length of medium side	length of long side
\(ABC\)	\(1\)	\(4\)	\(5\)	\(7\)
\(DEF\)	\(2\)
\(GHI\)	\(3\)
\(JKL\)	\(\frac{1}{2}\)

2. Your teacher will assign you one of the three columns. For all four triangles, find the quotient of the triangle side lengths assigned to you and record it in the table. What do you notice about the quotients?

Table \(\PageIndex{2}\)

triangle	(long side) \(\div\) (short side)	(long side) \(\div\) (medium side)	(medium side) \(\div\) (short side)
\(ABC\)	\(\frac{7}{4}\) or \(1.75\)
\(DEF\)
\(GHI\)
\(JKL\)

3. Compare your results with your partner's and complete your table.

Are you ready for more?

Triangle \(ABC\) and \(DEF\) are similar. Explain why \(\frac{AB}{BC}=\frac{DE}{EF}\).

Figure \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\): Using Side Quotients to Find Side Lengths of Similar Triangles

Triangles \(ABC\), \(EFD\), and \(GHI\) are all similar. The side lengths of the triangles all have the same units. Find the unknown side lengths.

Figure \(\PageIndex{3}\): Three triangles. Vertices capital A, B C. Sides B C and A, C length 4. Side A, B length lower-case c. Vertices capital I H G. Side I G length lower-case h. Side I H length fraction 12 over 5. Side H G length fraction 6 over 5. Vertices capital D E F. Side E F 5, Side F D length lower-case e, side E D length lowercase d.

Summary

If two polygons are similar, then the side lengths in one polygon are multiplied by the same scale factor to give the corresponding side lengths in the other polygon.

For these triangles the scale factor is 2:

Figure \(\PageIndex{4}\)

Here is a table that shows relationships between the short and medium length sides of the small and large triangle.

Table \(\PageIndex{3}\)

	small triangle	large triangle
medium side	\(4\)	\(8\)
short side	\(3\)	\(6\)
(medium side) \(\div\) (short side)	\(\frac{4}{3}\)	\(\frac{8}{6}=\frac{4}{3}\)

The lengths of the medium side and the short side are in a ratio of \(4\) : \(3\). This means that the medium side in each triangle is \(\frac{4}{3}\) as long as the short side. This is true for all similar polygons; the ratio between two sides in one polygon is the same as the ratio of the corresponding sides in a similar polygon.

We can use these facts to calculate missing lengths in similar polygons. For example, triangles \(A'B'C'\) and \(ABC\) shown here are similar. Let's find the length of segment \(B'C'\).

In triangle \(ABC\), side \(BC\) is twice as long as side \(AB\), so this must be true for any triangle that is similar to triangle \(ABC\). Since \(A'B'\) is 1.2 units long and \(2\cdot 1.2 =2.4\), the length of side \(B'C'\) is 2.4 units.

Figure \(\PageIndex{5}\)

Glossary Entries

Definition: Similar

Two figures are similar if one can fit exactly over the other after rigid transformations and dilations.

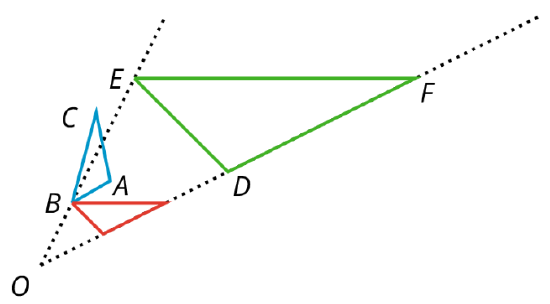
In this figure, triangle \(ABC\) is similar to triangle \(DEF\).

If \(ABC\) is rotated around point \(B\) and then dilated with center point \(O\), then it will fit exactly over \(DEF\). This means that they are similar.

Figure \(\PageIndex{6}\)

Practice

Exercise \(\PageIndex{4}\)

These two triangles are similar. What are \(a\) and \(b\)? Note: the two figures are not drawn to scale.

Figure \(\PageIndex{7}\)

Exercise \(\PageIndex{5}\)

Here is triangle \(ABC\). Triangle \(XYZ\) is similar to \(ABC\) with scale factor \(\frac{1}{4}\).

Figure \(\PageIndex{8}\)

1. Draw what triangle \(XYZ\) might look like.
2. How do the angle measures of triangle \(XYZ\) compare to triangle \(ABC\)? Explain how you know.
3. What are the side lengths of triangle \(XYZ\)?
4. For triangle \(XYZ\), calculate (long side) \(\div\) (medium side), and compare to triangle \(ABC\).

Exercise \(\PageIndex{6}\)

The two triangles shown are similar. Find the value of \(\frac{d}{c}\).

Figure \(\PageIndex{9}\)

Exercise \(\PageIndex{7}\)

The diagram shows two nested triangles that share a vertex. Find a center and a scale factor for a dilation that would move the larger triangle to the smaller triangle.

Figure \(\PageIndex{10}\): Coordinate plane, x, negative 9 to 3, y, negative 2 to 7. A line through negative 6 comma 6 and the origin. A triangle connecting negative 6 comma 6, to negative 6 comma 1, to negative 1 comma 1. Another triangle connecting negative 2 comma 2, to negative 2 comma 1, to negative 1 comma 1.

(From Unit 2.1.5)