5.5.4: The Volume of a Sphere
- Page ID
- 36046
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Lesson
Let's explore spheres and their volumes.
Exercise \(\PageIndex{1}\): Sketch a Sphere
Here is a method for quickly sketching a sphere:
- Draw a circle.
- Draw an oval in the middle whose edges touch the sphere.
- Practice sketching some spheres. Sketch a few different sizes.
- For each sketch, draw a radius and label it \(r\).
Exercise \(\PageIndex{2}\): A Sphere in a Cylinder

Here are a cone, a sphere, and a cylinder that all have the same radii and heights. The radius of the cylinder is 5 units. When necessary, express all answers in terms of \(\pi\).
- What is the height of the cylinder?
- What is the volume of the cylinder?
- What is the volume of the cone?
- What is the volume of the sphere? Explain your reasoning.
Exercise \(\PageIndex{3}\): Spheres in Cylinders

Here are a cone, a sphere, and a cylinder that all have the same radii and heights. Let the radius of the cylinder be \(r\) units. When necessary, express answers in terms of \(\pi\).
- What is the height of the cylinder in terms of \(r\)?
- What is the volume of the cylinder in terms of \(r\)?
- What is the volume of the cone in terms of \(r\)?
- What is the volume of the sphere in terms of \(r\)?
- A volume of the cone is \(\frac{1}{3}\) the volume of a cylinder. The volume of the sphere is what fraction of the volume of the cylinder?
Summary
Think about a sphere with radius \(r\) units that fits snugly inside a cylinder. The cylinder must then also have a radius of \(r\) units and a height of \(2r\) units. Using what we have learned about volume, the cylinder has a volume of \(\pi r^{2}h=\pi r^{2}\cdot (2r)\), which is equal to \(2\pi r^{3}\) cubic units.
We know from an earlier lesson that the volume of a cone with the same base and height as a cylinder has \(\frac{1}{3}\) of the volume. In this example, such a cone has a volume of \(\frac{1}{3}\cdot \pi r^{2}\cdot 2r\) or just \(\frac{2}{3}\pi r^{3}\) cubic units.
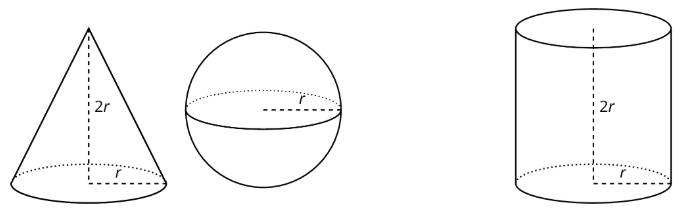
If we filled the cone and sphere with water, and then poured that water into the cylinder, the cylinder would be completely filled. That means the volume of the sphere and the volume of the cone add up to the volume of the cylinder. In other words, if \(V\) is the volume of the sphere, then
\(V+\frac{2}{3}\pi r^{3}=2\pi r^{3}\)
This leads to the formula for the volume of the sphere,
\(V=\frac{4}{3}\pi r^{3}\)
Practice
Exercise \(\PageIndex{4}\)
- A cube's volume is 512 cubic units. What is the length of its edge?
- If a sphere fits snugly inside this cube, what is its volume?
- What fration of the cube is taken up by the sphere? What percentage is this? Explain or show your reasoning.
Exercise \(\PageIndex{5}\)
Sphere A has radius 2 cm. Sphere B has radius 4 cm.
- Calculate the volume of each sphere.
- The radius of Sphere B is double that of Sphere A. How many times greater is the volume of B?
Exercise \(\PageIndex{6}\)
Three cones have a volume of \(192\pi\) cm3. Cone A has a radius of 2 cm. Cone B has a radius of 3 cm. Cone C has a radius of 4 cm. Find the height of each cone.
(From Unit 5.4.6)
Exercise \(\PageIndex{7}\)
The graph represents the average price of regular gasoline in the United States in dollars as a function of the number of months after January 2014.
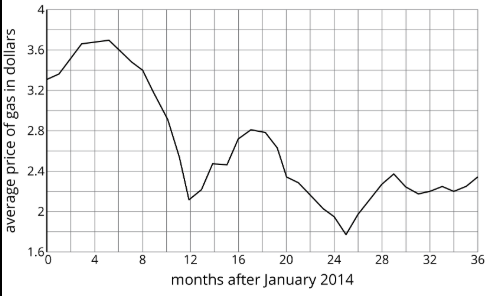
- How many months after January 2014 was the price of gas the greatest?
- Did the average price of gas ever get below $2?
- Describe what happened to the average price of gas in 2014.
(From Unit 5.2.3)
Exercise \(\PageIndex{8}\)
Match the description of each sphere to its correct volume.
- Sphere A: radius of 4 cm
- Sphere B: diameter of 6 cm
- Sphere C: radius of 8 cm
- Sphere D: radius of 6 cm
- \(288\pi\text{ cm}^{3}\)
- \(\frac{256}{3}\pi\text{ cm}^{3}\)
- \(36\pi\text{ cm}^{3}\)
- \(\frac{2048}{3}\pi\text{ cm}^{3}\)
Exercise \(\PageIndex{9}\)
While conducting an inventory in their bicycle shop, the owner noticed the number of bicycles is 2 fewer than 10 times the number of tricycles. They also know there are 410 wheels on all the bicycles and tricycles in the store. Write and solve a system of equations to find the number of bicycles in the store.
(From Unit 4.3.6)


