5.6.1: Volume as a Function of ...
- Page ID
- 36042
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Lesson
Let's compare water heights in different containers.
Exercise \(\PageIndex{1}\): Missing Information
A cylinder and sphere have the same height.
- If the sphere has a volume of \(36\pi\) cubic units, what is the height of the cylinder?
- What is a possible volume for the cylinder? Be prepared to explain your reasoning.
Exercise \(\PageIndex{2}\): Scaling Volume of a Sphere
- Fill in the missing volumes in terms of \(\pi\). Add two more radius and volume pairs of your choosing.
radius \(1\) \(2\) \(3\) \(\frac{1}{2}\) \(\frac{1}{3}\) \(100\) \(r\) volume \(\frac{4}{3}\pi\) Table \(\PageIndex{1}\) - How does the volume of a sphere with radius 2 cm compare to the volume of a sphere with radius 1 cm
- How does the volume of a sphere with radius \(\frac{1}{2}\) cm compare to the volume of a sphere with radius 1 cm?
- A sphere has a radius of length \(r\).
- What happens to the volume of this sphere if its radius is doubled?
- What happens to the volume of this sphere if its radius is halved?
- Sphere Q has a volume of 500 cm3. Sphere S has a radius \(\frac{1}{5}\) as large as Sphere Q. What is the volume of Sphere S?
Exercise \(\PageIndex{3}\): A Cylinder, a Cone, and a Sphere
Three containers of the same height were filled with water at the same rate. One container is a cylinder, one is a cone, and one is a sphere. As they were filled, the relationship between the volume of water and the height of the water was recorded in different ways, shown here:
- Cylinder: \(h=\frac{V}{4\pi}\)
- Cone:
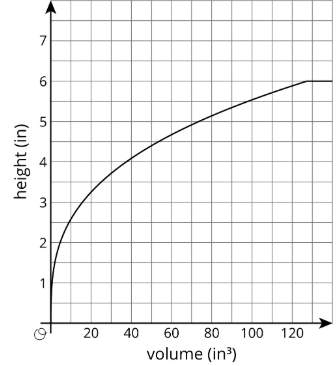
- Sphere:
| volume (in\(^{3}\)) | height (in) |
|---|---|
| 0 | 0 |
| 8.38 | 1 |
| 29.32 | 2 |
| 56.55 | 3 |
| 83.76 | 4 |
| 104.72 | 5 |
| 113.04 | 6 |
| 120 | 6 |
| 200 | 6 |
- The maximum volume of water the cylinder can hold is \(24\pi\). What is the radius of the cylinder?
- Graph the relationship between the volume of water poured into the cylinder and the height of water in the cylinder on the same axes as the cone. What does the slope of this line represent?
- Which container can fit the largest volume of water? The smallest?
- About how much water does it take for the cylinder and the sphere to have the same height? The cylinder and the cone? Explain how you know.
- For what approximate range of volumes is the height of the water in the cylinder greater than the height of the water in the cone? Explain how you know.
- For what approximate range of volumes is the height of the water in the sphere less than the height of the water in the cylinder? Explain how you know.