7.2.5: What about Other Bases?

Lesson

Let's explore exponent patterns with bases other than 10.

Exercise \(\PageIndex{1}\): True or False: Comparing Expressions with Exponents

Is each statement true or false? Be prepared to explain your reasoning.

1. \(3^{5}<4^{6}\)
2. \((-3)^{2}<3^{2}\)
3. \((-3)^{3}=3^{3}\)
4. \((-5)^{2}>-5^{2}\)

Exercise \(\PageIndex{2}\): What Happens with Zero and Negative Exponents?

Complete the table to show what it means to have an exponent of zero or a negative exponent.

Figure \(\PageIndex{1}\): A table with two rows. First row, value, 16, 4 blanks, fraction 1 over 2, three blanks. Second row, exponent form, 2 to the fourth power, 8 blanks. Above the top row, arrows point column to column right to left, labeled time 2. Below the bottom row, arrows point column to column, left to right, labeled times question mark.

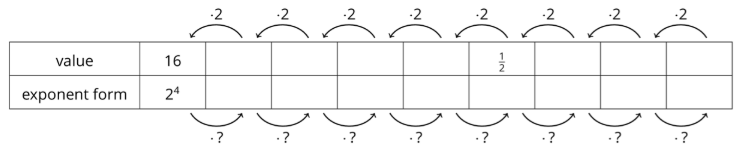
1. As you move toward the left, each number is being multiplied by 2. What is the multiplier as you move toward the right?
2. Use the patterns you found in the table to write \(2^{-6}\) as a fraction.
3. Write \(\frac{1}{32}\) as a power of 2 with a single exponent.
4. What is the value of \(2^{0}\)?
5. From the work you have done with negative exponents, how would you write \(5^{-3}\) as a fraction?
6. How would you write \(3^{-4}\) as a fraction?

Are you ready for more?

1. Find an expression equivalent to \(\left(\frac{2}{3}\right)^{-3}\) but with positive exponents.
2. Find an expression equivalent to \(\left(\frac{4}{5}\right)^{-8}\) but with positive exponents.
3. What patterns do you notice when you start with a fraction raised to a negative exponent and rewrite it using a single positive exponent? Show or explain your reasoning.

Exercise \(\PageIndex{3}\): Exponent Rules with Bases Other than 10

Lin, Noah, Diego, and Elena decide to test each other’s knowledge of exponents with bases other than 10. They each chose an expression to start with and then came up with a new list of expressions; some of which are equivalent to the original and some of which are not.

Choose 2 of the 4 lists to analyze. For each list of expressions you choose to analyze, decide which expressions are not equivalent to the original. Be prepared to explain your reasoning.

1. Lin's original expression is \(5^{-9}\) and her list is:
   \[(5^{3})^{-3}\qquad -5^{9}\qquad \frac{5^{-6}}{5^{3}}\qquad(5^{3})^{-2}\qquad\frac{5^{-4}}{5^{-5}}\qquad 5^{-4}\cdot 5^{-5}\nonumber\]
2. Noah's original expression is \(3^{10}\) and his list is:
   \[3^{5}\cdot 3^{2}\qquad (3^{5})^{2}\qquad (3\cdot 3)(3\cdot 3)(3\cdot 3)(3\cdot 3)\qquad \left(\frac{1}{3}\right)^{-10}\qquad 3^{7}\cdot 3^{3}\qquad\frac{3^{20}}{3^{10}}\qquad\frac{3^{20}}{3^{2}}\nonumber\]
3. Diego's original expression is \(x^{4}\) and his list is:
   \[\frac{x^{8}}{x^{4}}\qquad x\cdot x\cdot x\cdot x\qquad\frac{x^{-4}}{x^{-8}}\qquad\frac{x^{-4}}{x^{8}}\qquad (x^{2})^{2}\qquad 4\cdot x\qquad x\cdot x^{3}\nonumber\]
4. Elena's original expression is \(8^{0}\) and her list is:
   \[1\qquad 0\qquad 8^{3}\cdot 8^{-3}\qquad\frac{8^{2}}{8^{2}}\qquad 10^{0}\qquad 11^{0}\nonumber\]

Summary

Earlier we focused on powers of 10 because 10 plays a special role in the decimal number system. But the exponent rules that we developed for 10 also work for other bases. For example, if \(2^{0}=1\) and \(2^{-n}=\frac{1}{2^{n}}\), then

\[\begin{aligned}2^{m}\cdot 2^{n}&=2^{m+n}\\ (2^{m})^{n}&=2^{m\cdot n} \\ \frac{2^{m}}{2^{n}}&=2^{m-n}\end{aligned}\nonumber\]

These rules also work for powers of numbers less than 1. For example, \(\left(\frac{1}{3}\right)^{2}=\frac{1}{3}\cdot\frac{1}{3}\) and \(\left(\frac{1}{3}\right)^{4}=\frac{1}{3}\cdot\frac{1}{3}\cdot\frac{1}{3}\cdot\frac{1}{3}\). We can also check that \(\left(\frac{1}{3}\right)^{2}\cdot\left(\frac{1}{3}\right)^{4}=\left(\frac{1}{3}\right)^{2+4}\).

Using a variable \(x\) helps to see this structure. Since \(x^{2}\cdot x^{5}=x^{7}\) (both sides have 7 factors that are \(x\)), if we let \(x=4\), we can see that \(4^{2}\cdot 4^{5}=4^{7}\). Similarly, we could let \(x=\frac{2}{3}\) or \(x=11\) or any other positive value and show that these relationships still hold.

Glossary Entries

Definition: Base (of an exponent)

In expressions like \(5^{3}\) and \(8^{2}\), the 5 and the 8 are called bases. They tell you what factor to multiply repeatedly. For example, \(5^{3}=5\cdot 5\cdot 5\), and \(8^{2}=8\cdot 8\).

Practice

Exercise \(\PageIndex{4}\)

Priya says “I can figure out \(5^{0}\) by looking at other powers of 5. \(5^{3}\) is 125, \(5^{2}\) is 25, then \(5^{1}\) is 5.”

1. What pattern do you notice?
2. If this pattern continues, what should be the value of \(5^{0}\)? Explain how you know.
3. If this pattern continues, what should be the value of \(5^{-1}\)? Explain how you know.

Exercise \(\PageIndex{5}\)

Select all the expressions that are equivalent to \(4^{-3}\).

1. \(-12\)
2. \(2^{-6}\)
3. \(\frac{1}{4^{3}}\)
4. \(\left(\frac{1}{4}\right)\cdot\left(\frac{1}{4}\right)\cdot\left(\frac{1}{4}\right)\)
5. \(12\)
6. \((-4)\cdot (-4)\cdot (-4)\)
7. \(\frac{8^{-1}}{2^{2}}\)

Exercise \(\PageIndex{6}\)

Write each expression using a single exponent.

1. \(\frac{5^{3}}{5^{6}}\)
2. \((14^{3})^{6}\)
3. \(8^{3}\cdot 8^{6}\)
4. \(\frac{16^{6}}{16^{3}}\)
5. \((21^{3})^{-6}\)

Exercise \(\PageIndex{7}\)

Andre sets up a rain gauge to measure rainfall in his back yard. On Tuesday, it rains off and on all day.

• He starts at 10 a.m. with an empty gauge when it starts to rain.
• Two hours later, he checks, and the gauge has 2 cm of water in it.
• It starts raining even harder, and at 4 p.m., the rain stops, so Andre checks the rain gauge and finds it has 10 cm of water in it.
• While checking it, he accidentally knocks the rain gauge over and spills most of the water, leaving only 3 cm of water in the rain gauge.
• When he checks for the last time at 5 p.m., there is no change.

Graph A

Figure \(\PageIndex{2}\): Line graph, horizontal axis labeled 10, 11, 12, 1, 2, 3, 4, 5, 6. Vertical, 0 to 12 by 2. Segments, 10 comma 0 to 12 comma 2, then to 4 comma 10, closed circles. An open circle at 4 comma 3 connects to a closed circle at 5 comma 3.

Graph B

Figure \(\PageIndex{3}\)

1. Which of the two graphs could represent Andre’s story? Explain your reasoning.
2. Label the axes of the correct graph with appropriate units.
3. Use the graph to determine how much total rain fell on Tuesday.

(From Unit 5.2.4)