8.2.4: The Converse

Lesson

Let's figure out if a triangle is a right triangle.

Exercise \(\PageIndex{1}\): The Hands of a Clock

Consider the tips of the hands of an analog clock that has an hour hand that is 3 centimeters long and a minute hand that is 4 centimeters long.

Figure \(\PageIndex{1}\): The image of a circle that represent an analog clock. On the circle are 12 evenly spaced tick marks. There are two hands on the clock. One hand is labeled 3, begins in the center of the circle and extends upward and to the right, and points to the third tick mark from the top. The other hand is labeled 4, begins in the center of the circle and extends upward and to the left. It points to the eleventh tick mark from the top.

Over the course of a day:

1. What is the farthest apart the two tips get?
2. What is the closest the two tips get?
3. Are the two tips ever exactly five centimeters apart?

Exercise \(\PageIndex{2}\): Proving the Converse

Here are three triangles with two side lengths measuring 3 and 4 units, and the third side of unknown length.

Figure \(\PageIndex{2}\): A figure of three triangles each with 2 given side lengths and one unknown side length. The first triangle has a horizontal side of 4, a side length slanted upward and to the left of 3, and the third side length labeled x. The middle triangle has a horizontal side length of 4, a second side length slanted upward and to the right of 3, and the third side length labeled y. The third triangle is a right triangle with a horizontal side length of 4, a vertical side length of 3, and the third side is labeled z.

Sort the following six numbers from smallest to largest. Put an equal sign between any you know to be equal. Be ready to explain your reasoning.

\(1\quad 5\quad 7\quad x\quad y\quad z\)

Are you ready for more?

A related argument also lets us distinguish acute from obtuse triangles using only their side lengths.

Decide if triangles with the following side lengths are acute, right, or obtuse. In right or obtuse triangles, identify which side length is opposite the right or obtuse angle.

• \(x=15,\quad y=20,\quad z=8\)
• \(x=8,\quad y=15,\quad z=13\)
• \(x=17,\quad y=8,\quad z=15\)

Exercise \(\PageIndex{3}\): Calculating Legs of Right Triangles

1. Given the information provided for the right triangles shown here, find the unknown leg lengths to the nearest tenth.

Figure \(\PageIndex{3}\): Two right triangles are indicated. The triangle on the left has two leg with lengths of 2 and a. The hypotenuse has a length of 7. The triangle on the right has two legs with length x and a hypotenuse of length 4.

2. The triangle shown here is not a right triangle. What are two different ways you change one of the values so it would be a right triangle? Sketch these new right triangles, and clearly label the right angle.

Figure \(\PageIndex{4}\)

Summary

What if it isn’t clear whether a triangle is a right triangle or not? Here is a triangle:

Figure \(\PageIndex{5}\)

Is it a right triangle? It’s hard to tell just by looking, and it may be that the sides aren’t drawn to scale.

If we have a triangle with side lengths \(a\), \(b\), and \(c\), with \(c\) being the longest of the three, then the converse of the Pythagorean Theorem tells us that any time we have \(a^{2}+b^{2}=c^{2}\), we must have a right triangle. Since \(8^{2}+15^{2}=64+225=289=17^{2}\), any triangle with side lengths 8, 15, and 17 must be a right triangle.

Together, the Pythagorean Theorem and its converse provide a one-step test for checking to see if a triangle is a right triangle just using its side lengths. If \(a^{2}+b^{2}=c^{2}\), it is a right triangle. If \(a^{2}+b^{2}\neq c^{2}\), it is not a right triangle.

Glossary Entries

Definition: Pythagorean Theorem

The Pythagorean Theorem describes the relationship between the side lengths of right triangles.

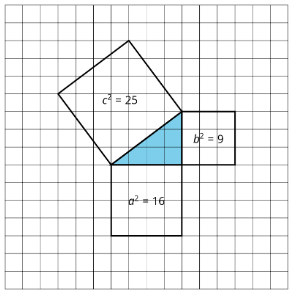
The diagram shows a right triangle with squares built on each side. If we add the areas of the two small squares, we get the area of the larger square.

The square of the hypotenuse is equal to the sum of the squares of the legs. This is written as \(a^{2}+b^{2}=c^{2}\).

Figure \(\PageIndex{6}\)

Definition: Hypotenuse

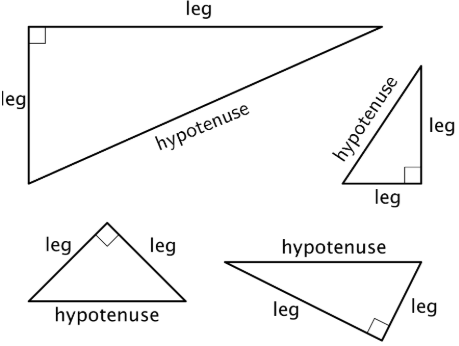
The hypotenuse is the side of a right triangle that is opposite the right angle. It is the longest side of a right triangle.

Here are some right triangles. Each hypotenuse is labeled.

Figure \(\PageIndex{7}\)

Definition: LEgs

The legs of a right triangle are the sides that make the right angle.

Here are some right triangles. Each leg is labeled.

Figure \(\PageIndex{8}\)

Practice

Exercise \(\PageIndex{4}\)

Which of these triangles are definitely right triangles? Explain how you know. (Note that not all triangles are drawn to scale.)

Figure \(\PageIndex{9}\)

Exercise \(\PageIndex{5}\)

A right triangle has a hypotenuse of 15 cm. What are possible lengths for the two legs of the triangle? Explain your reasoning.

Figure \(\PageIndex{10}\)

Exercise \(\PageIndex{6}\)

In each part, \(a\) and \(b\) represent the length of a leg of a right triangle, and \(c\) represents the length of its hypotenuse. Find the missing length, given the other two lengths.

1. \(a=12,\quad b=5,\quad c=?\)
2. \(a=?,\quad b=21,\quad c=29\)

(From Unit 8.2.3)

Exercise \(\PageIndex{7}\)

For which triangle does the Pythagorean Theorem express the relationship between the lengths of its three sides?

Figure \(\PageIndex{11}\)

(From Unit 8.2.1)

Exercise \(\PageIndex{8}\)

Andre makes a trip to Mexico. He exchanges some dollars for pesos at a rate of 20 pesos per dollar. While in Mexico, he spends 9000 pesos. When he returns, he exchanges his pesos for dollars (still at 20 pesos per dollar). He gets back \(\frac{1}{10}\) the amount he started with. Find how many dollars Andre exchanged for pesos and explain your reasoning. If you get stuck, try writing an equation representing Andre’s trip using a variable for the number of dollars he exchanged.

(From Unit 4.2.4)