1.1.5: The Size of the Scale Factor

Lesson

Let's look at the effects of different scale factors.

Exercise \(\PageIndex{1}\): Number Talk: Missing Factor

Solve each equation mentally.

\(16x=176\)

\(16x=8\)

\(16x=1\)

\(\frac{1}{5}x=1\)

\(\frac{2}{5}x=1\)

Exercise \(\PageIndex{2}\): Card Sort: Scaled Copies

Your teacher will give you a set of cards. On each card, Figure A is the original and Figure B is a scaled copy.

1. Sort the cards based on their scale factors. Be prepared to explain your reasoning.
2. Examine cards 10 and 13 more closely. What do you notice about the shapes and sizes of the figures? What do you notice about the scale factors?
3. Examine cards 8 and 12 more closely. What do you notice about the figures? What do you notice about the scale factors?

Are you ready for more?

Triangle B is a scaled copy of Triangle A with scale factor \(\frac{1}{2}\).

1. How many times bigger are the side lengths of Triangle B when compared with Triangle A?
2. Imagine you scale Triangle B by a scale factor of \(\frac{1}{2}\) to get Triangle C. How many times bigger will the side lengths of Triangle C be when compared with Triangle A?
3. Triangle B has been scaled once. Triangle C has been scaled twice. Imagine you scale triangle A \(n\) times to get Triangle N, always using a scale factor of \(\frac{1}{2}\). How many times bigger will the side lengths of Triangle N be when compared with Triangle A?

Exercise \(\PageIndex{3}\): Scaling A Puzzle

Your teacher will give you 2 pieces of a 6-piece puzzle.

1. If you drew scaled copies of your puzzle pieces using a scale factor of \(\frac{1}{2}\), would they be larger or smaller than the original pieces? How do you know?

2. Create a scaled copy of each puzzle piece on a blank square, with a scale factor of \(\frac{1}{2}\).

3. When everyone in your group is finished, put all 6 of the original puzzle pieces together like this:

Figure \(\PageIndex{1}\)

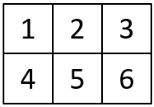
Next, put all 6 of your scaled copies together. Compare your scaled puzzle with the original puzzle. Which parts seem to be scaled correctly and which seem off? What might have caused those parts to be off?

4. Revise any of the scaled copies that may have been drawn incorrectly.

5. If you were to lose one of the pieces of the original puzzle, but still had the scaled copy, how could you recreate the lost piece?

Exercise \(\PageIndex{4}\): Missing Figure, Factor, or Copy

1. What is the scale factor from the original triangle to its copy? Explain or show your reasoning.

Figure \(\PageIndex{2}\)

2. The scale factor from the original trapezoid to its copy is 2. Draw the scaled copy.

Figure \(\PageIndex{3}\)

3. The scale factor from the original figure to its copy is \(\frac{3}{2}\). Draw the original figure.

Figure \(\PageIndex{4}\)

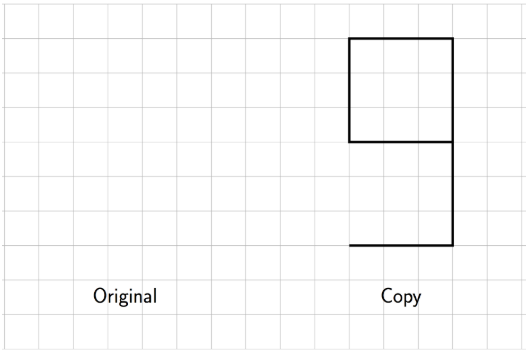
4. What is the scale factor from the original figure to the copy? Explain how you know.

Figure \(\PageIndex{5}\)

5. The scale factor from the original figure to its scaled copy is 3. Draw the scaled copy.

Figure \(\PageIndex{6}\): A triangle with the horizontal side extended to the right and the vertical side extended upward creating a figure that resembles the number 4. The figure is labeled original. On the right, the position labeled copy is blank.

Summary

The size of the scale factor affects the size of the copy. When a figure is scaled by a scale factor greater than 1, the copy is larger than the original. When the scale factor is less than 1, the copy is smaller. When the scale factor is exactly 1, the copy is the same size as the original.

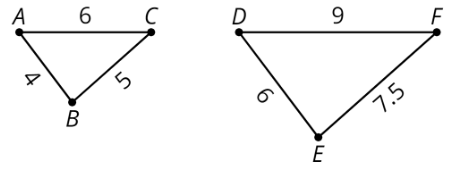
Triangle \(DEF\) is a larger scaled copy of triangle \(ABC\), because the scale factor from \(ABC\) to \(DEF\) is \(\frac{3}{2}\). Triangle \(ABC\) is a smaller scaled copy of triangle \(DEF\), because the scale factor from \(DEF\) to \(ABC\) is \(\frac{2}{3}\).

Figure \(\PageIndex{7}\): Two triangles; one labeled A B C with horizontal A B and the other D E F with horizontal D E. The length of A B is labeled 4. The length of B C is labeled 3. The length of C A is labeled 5. The length of D E is labeled 6. The length of E F is labeled 4.5. The length of F D is labeled 7.5. An arrow from triangle A B C pointing to triangle D E F is labeled, times 3 halves. An arrow from triangle D E F pointing to triangle A B C is labeled times 2 thirds.

This means that triangles \(ABC\) and \(DEF\) are scaled copies of each other. It also shows that scaling can be reversed using reciprocal scale factors, such as \(\frac{2}{3}\) and \(\frac{3}{2}\).

In other words, if we scale Figure A using a scale factor of 4 to create Figure B, we can scale Figure B using the reciprocal scale factor, \(\frac{1}{4}\), to create Figure A.

Glossary Entries

Definition: Corresponding

When part of an original figure matches up with part of a copy, we call them corresponding parts. These could be points, segments, angles, or distances.

For example, point \(B\) in the first triangle corresponds to point \(E\) in the second triangle. Segment \(AC\) corresponds to segment \(DF\).

Figure \(\PageIndex{8}\)

Definition: Reciprocal

Dividing 1 by a number gives the reciprocal of that number. For example, the reciprocal of 12 is \(\frac{1}{12}\), and the reciprocal of \(\frac{2}{5}\) is \(\frac{5}{2}\).

Definition: Scale Factor

To create a scaled copy, we multiply all the lengths in the original figure by the same number. This number is called the scale factor.

In this example, the scale factor is 1.5, because \(4\cdot (1.5)=6\), \(5\cdot (1.5)=7.5\), and \(6\cdot (1.5)=9\).

Figure \(\PageIndex{9}\)

Definition: Scaled Copy

A scaled copy is a copy of an figure where every length in the original figure is multiplied by the same number.

For example, triangle \(DEF\) is a scaled copy of triangle \(ABC\). Each side length on triangle \(ABC\) was multiplied by 1.5 to get the corresponding side length on triangle \(DEF\).

Figure \(\PageIndex{10}\)

Practice

Exercise \(\PageIndex{5}\)

Rectangles P, Q, R, and S are scaled copies of one another. For each pair, decide if the scale factor from one to the other is greater than 1, equal to 1, or less than 1.

Figure \(\PageIndex{11}\): Four rectangles, labeled P, Q, R and S. Each rectangle is a scaled copy of one another. Ranked in order from least to greatest, the area of the rectangles are as follows: the area of P is equal to S, which are less than the area of Q, which is less than the area of R.

1. from P to Q
2. from P to R
3. from Q to S
4. from Q to R
5. from S to P
6. from R to P
7. from P to S

Exercise \(\PageIndex{6}\)

Triangle S and Triangle L are scaled copies of one another.

1. What is the scale factor from S to L?
2. What is the scale factor from L to S?
3. Triangle M is also a scaled copy of S. The scale factor from S to M is \(\frac{3}{2}\). What is the scale factor from M to S?

Figure \(\PageIndex{12}\)

Exercise \(\PageIndex{7}\)

Are two squares with the same side lengths scaled copies of one another? Explain your reasoning.

Exercise \(\PageIndex{8}\)

Quadrilateral A has side lengths 2, 3, 5, and 6. Quadrilateral B has side lengths 4, 5, 8, and 10. Could one of the quadrilaterals be a scaled copy of the other? Explain.

(From Unit 1.1.2)

Exercise \(\PageIndex{9}\)

Select all the ratios that are equivalent to the ratio \(12:3\)

1. \(6:1\)
2. \(1:4\)
3. \(4:1\)
4. \(24:6\)
5. \(15:6\)
6. \(1,200:300\)
7. \(112:13\)