1.2.3: Creating Scale Drawings

Lesson

Let's create our own scale drawings.

Exercise \(\PageIndex{1}\): Number Talk: Which is Greater?

Without calculating, decide which quotient is larger.

\(11\div 23\) or \(7\div 13\)

\(0.63\div 2\) or \(0.55\div 3\)

\(15\div\frac{1}{3}\) or \(15\div\frac{1}{4}\)

Exercise \(\PageIndex{2}\): Bedroom Floor Plan

Here is a rough sketch of Noah’s bedroom (not a scale drawing).

Figure \(\PageIndex{1}\)

Noah wants to create a floor plan that is a scale drawing.

1. The actual length of Wall C is 4 m. To represent Wall C, Noah draws a segment 16 cm long. What scale is he using? Explain or show your reasoning.
2. Find another way to express the scale.
3. Discuss your thinking with your partner. How do your scales compare?
4. The actual lengths of Wall A, Wall B, and Wall D are 2.5 m, 2.75 m, and 3.75 m. Determine how long these walls will be on Noah’s scale floor plan.
5. Use the Point tool

Figure \(\PageIndex{2}\)

and the Segment tool

Figure \(\PageIndex{3}\)

to draw the walls of Noah's scale floor plan in the applet.

Are you ready for more?

If Noah wanted to draw another floor plan on which Wall C was 20 cm, would 1 cm to 5 m be the right scale to use? Explain your reasoning.

Exercise \(\PageIndex{3}\): Two Maps of Utah

A rectangle around Utah is about 270 miles wide and about 350 miles tall. The upper right corner that is missing is about 110 miles wide and about 70 miles tall.

1. Make a scale drawing of Utah where 1 centimeter represents 50 miles.
   Make a scale drawing of Utah where 1 centimeter represents 75 miles.
2. How do the two drawings compare? How does the choice of scale influence the drawing?

Summary

If we want to create a scale drawing of a room's floor plan that has the scale “1 inch to 4 feet,” we can divide the actual lengths in the room (in feet) by 4 to find the corresponding lengths (in inches) for our drawing.

Figure \(\PageIndex{4}\)

Suppose the longest wall is 15 feet long. We should draw a line 3.75 inches long to represent this wall, because \(15\div 4=3.75\).

There is more than one way to express this scale. These three scales are all equivalent, since they represent the same relationship between lengths on a drawing and actual lengths:

• \(1\) inch to \(4\) feet
• \(\frac{1}{2}\) inch to \(2\) feet
• \(\frac{1}{4}\) inch to \(1\) foot

Any of these scales can be used to find actual lengths and scaled lengths (lengths on a drawing). For instance, we can tell that, at this scale, an 8-foot long wall should be 2 inches long on the drawing because \(\frac{1}{4}\cdot 8=2\).

The size of a scale drawing is influenced by the choice of scale. For example, here is another scale drawing of the same room using the scale 1 inch to 8 feet.

Figure \(\PageIndex{5}\)

Notice this drawing is smaller than the previous one. Since one inch on this drawing represents twice as much actual distance, each side length only needs to be half as long as it was in the first scale drawing.

Glossary Entries

Definition: Scale

A scale tells how the measurements in a scale drawing represent the actual measurements of the object.

For example, the scale on this floor plan tells us that 1 inch on the drawing represents 8 feet in the actual room. This means that 2 inches would represent 16 feet, and \(\frac{1}{2}\) inch would represent 4 feet.

Figure \(\PageIndex{6}\)

Definition: Scale Drawing

A scale drawing represents an actual place or object. All the measurements in the drawing correspond to the measurements of the actual object by the same scale.

Figure \(\PageIndex{7}\)

Practice

Exercise \(\PageIndex{4}\)

An image of a book shown on a website is 1.5 inches wide and 3 inches tall on a computer monitor. The actual book is 9 inches wide.

1. What scale is being used for the image?
2. How tall is the actual book?

Exercise \(\PageIndex{5}\)

The flag of Colombia is a rectangle that is 6 ft long with three horizontal strips.

Figure \(\PageIndex{8}\): A rectangular figure that represents a flag. The rectangle is divided by two horizontal lines. The first horizontal line is drawn dividing the rectangle in half and the top half is shaded yellow. The second horizontal line is drawn halfway between the first horizontal line and the base of the rectangle. The middle section is shaded blue and the bottom section is shaded red. Flag of Colombia, by SKopp. Public Domain. Wikimedia Commons. Source.

• The top stripe is 2 ft tall and is yellow.
• The middle stripe is 1 ft tall and is blue.
• The bottom stripe is also 1 ft tall and is red.

1. Create a scale drawing of the Colombian flag with a scale of 1 cm to 2 ft.
2. Create a scale drawing of the Colombian flag with a scale of 2 cm to 1 ft.

Exercise \(\PageIndex{6}\)

These triangles are scaled copies of each other.

Figure \(\PageIndex{9}\): Four right triangles labeled F, B, G, and H. Triangle F has the vertical side labeled 8, the horizontal side labeled 6, and the longest side labeled 10. Triangle B has the vertical side labeled 2, the horizontal side labeled 3 halves, and the longest side labeled 5 halves. Triangle G has the vertical side labeled 4, the horizontal side labeled 3, and the longest side labeled 5. Triangle H has the vertical side labeled 8 thirds, the horizontal side labeled 2, and the longest side labeled 10 thirds.

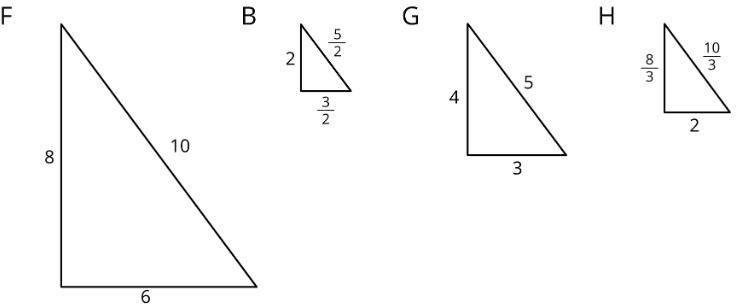
For each pair of triangles listed, the area of the second triangle is how many times larger than the area of the first?

1. Triangle G and Triangle F
2. Triangle G and Triangle B
3. Triangle B and Triangle F
4. Triangle F and Triangle H
5. Triangle G and Triangle H
6. Triangle H and Triangle B

(From Unit 1.1.6)

Exercise \(\PageIndex{7}\)

Here is an unlabeled rectangle, followed by other quadrilaterals that are labeled.

Figure B has side lengths 8, 3, 8, 3. C has side lengths 6, 3, 6, 3. D has 2, 1, 2, 1. E has 4, 2, 4, 2. F has 7, diagonal side down 3, right 1, 7, and diagonal side left 1, up 3. G has 5, 2, 5, 2. H has 8, 4, 8, 4.

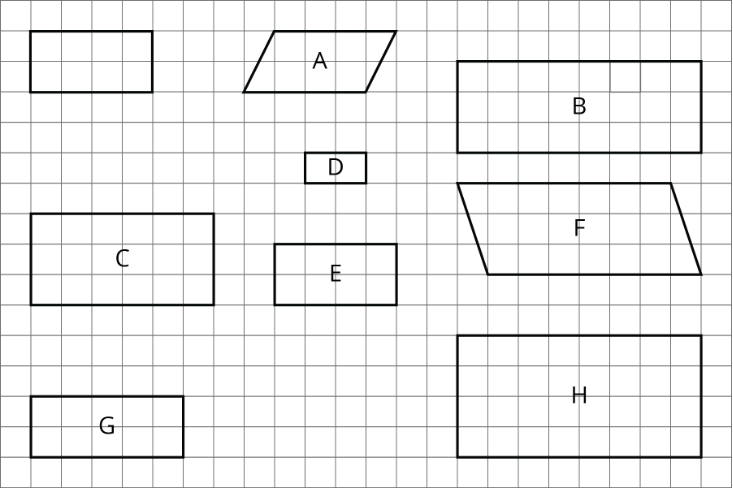
1. Select all quadrilaterals that are scaled copies of the unlabeled rectangle. Explain how you know.
2. On graph paper, draw a different scaled version of the original rectangle.

(From Unit 1.1.3)