3.3.1: Distinguishing Circumference and Area

Lesson

Let's contrast circumference and area.

Exercise \(\PageIndex{1}\): Filling the Plate

About how many cheese puffs can fit on the plate in a single layer? Be prepared to explain your reasoning.

Figure \(\PageIndex{1}\): A picture of a tray with covered with one layer of circular cheese puffs. On top of the cheese puffs is a circular plate with 1 cheese puff placed in the center of the plate. The diameter of the plate is approximately the same as the width of the tray. Approximately 14 cheese puffs are used to measure the width of the tray. Cheese Balls, by Andrew Stadel . CC BY-SA. Estimation 180. Source.

Exercise \(\PageIndex{2}\): Cart Sort: Circle Problems

Your teacher will give you cards with questions about circles.

1. Sort the cards into two groups based on whether you would use the circumference or the area of the circle to answer the question. Pause here so your teacher can review your work.
2. Your teacher will assign you a card to examine more closely. What additional information would you need in order to answer the question on your card?
3. Estimate measurements for the circle on your card.
4. Use your estimates to calculate the answer to the question.

Exercise \(\PageIndex{3}\): Visual Display of Circle Problem

In the previous activity you estimated the answer to a question about circles.

Create a visual display that includes:

• The question you were answering
• A diagram of a circle labeled with your estimated measurements
• Your thinking, organized so that others can follow it
• Your answer, expressed in terms of \(\pi\) and also expressed as a decimal approximation

Exercise \(\PageIndex{4}\): Analyzing Circle Claims

Here are two students’ answers for each question. Do you agree with either of them? Explain or show your reasoning.

1. How many feet are traveled by a person riding once around the merry-go-round?

Figure \(\PageIndex{2}\)

• Clare says, “The radius of the merry-go-round is about 4 feet, so the distance around the edge is about \(8\pi\) feet.”
• Andre says, “The diameter of the merry-go-round is about 4 feet, so the distance around the edge is about \(4\pi\) feet.”

2. How much room is there to spread frosting on the cookie?

Figure \(\PageIndex{3}\)

• Clare says “The radius of the cookie is about 3 centimeters, so the space for frosting is about \(6\pi\) cm².”
• Andre says “The diameter of the cookie is about 3 inches, so the space for frosting is about \(2.25\pi\) in².”

3. How far does the unicycle move when the wheel makes 5 full rotations?

Figure \(\PageIndex{4}\)

• Clare says, “The diameter of the unicycle wheel is about 0.5 meters. In 5 complete rotations it will go about \(\frac{5}{2}\pi\) m².”
• Andre says, “I agree with Clare's estimate of the diameter, but that means the unicycle will go about \(\frac{5}{4}\pi\) m.”

Are you ready for more?

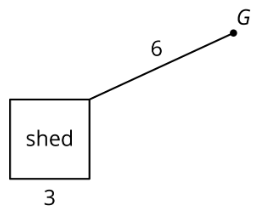
A goat (point \(G\)) is tied with a 6-foot rope to the corner of a shed. The floor of the shed is a square whose sides are each 3 feet long. The shed is closed and the goat can't go inside. The space all around the shed is flat, grassy, and the goat can't reach any other structures or objects. What is the area over which the goat can roam?

Figure \(\PageIndex{5}\): Square, side length = 3 units. Square labeled shed. Line segment from top right corner of square, running up and to the right diagonally, ends at point labeled G. Line segment labeled 6.

Summary

Sometimes we need to find the circumference of a circle, and sometimes we need to find the area. Here are some examples of quantities related to the circumference of a circle:

• The length of a circular path.
• The distance a wheel will travel after one complete rotation.
• The length of a piece of rope coiled in a circle.

Here are some examples of quantities related to the area of a circle:

• The amount of land that is cultivated on a circular field.
• The amount of frosting needed to cover the top of a round cake.
• The number of tiles needed to cover a round table.

In both cases, the radius (or diameter) of the circle is all that is needed to make the calculation. The circumference of a circle with radius \(r\) is \(2\pi r\) while its area is \(\pi r^{2}\). The circumference is measured in linear units (such as cm, in, km) while the area is measured in square units (such as cm², in², km²).

Practice

Exercise \(\PageIndex{5}\)

For each problem, decide whether the circumference of the circle or the area of the circle is most useful for finding a solution. Explain your reasoning.

1. A car’s wheels spin at 1000 revolutions per minute. The diameter of the wheels is 23 inches. You want to know how fast the car is travelling.
2. A circular kitchen table has a diameter of 60 inches. You want to know how much fabric is needed to cover the table top.
3. A circular puzzle is 20 inches in diameter. All of the pieces are about the same size. You want to know about how many pieces there are in the puzzle.
4. You want to know about how long it takes to walk around a circular pond.

Exercise \(\PageIndex{6}\)

The city of Paris, France is completely contained within an almost circular road that goes around the edge. Use the map with its scale to:​

1. Estimate the circumference of Paris.
2. Estimate the area of Paris.

Figure \(\PageIndex{6}\): Map of the city of Paris, France. Paris is completely contained within an almost circular road. Map scale indicates 1 mile = a line segment that is approximately one sixth of the diameter of the circle. By United States Census Bureau. Public Domain. American Fact Finder. Source.

Exercise \(\PageIndex{7}\)

Here is a diagram of a softball field:

Figure \(\PageIndex{7}\): A quarter-circle that represents the diagram of a softball field. A small circular-like region inside the quarter-circle is labeled Infield and a dashed line goes through the center of the circular region connecting to two points on its edge is labeled 110 ft. The area outside of the circular region is labeled Outfield and the horizontal base of the quarter-circle is labeled 250 ft.

1. About how long is the fence around the field?
2. About how big is the outfield?

Exercise \(\PageIndex{8}\)

While in math class, Priya and Kiran come up with two ways of thinking about the proportional relationship shown in the table.

Table \(\PageIndex{1}\)

\(x\)	\(y\)
\(2\)	?
\(5\)	\(1750\)

Both students agree that they can solve the equation \(5k=1750\) to find the constant of proportionality.

• Priya says, “I can solve this equation by dividing 1750 by 5.”
• Kiran says, “I can solve this equation by multiplying 1750 by \(\frac{1}{5}\).”

1. What value of \(k\) would each student get using their own method?
2. How are Priya and Kiran's approaches related?
3. Explain how each student might approach solving the equation \(\frac{2}{3}k=50\).

(From Unit 2.2.2)