5.2.1: Changing Temperatures
- Page ID
- 38329
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lesson
Let's add signed numbers.
Exercise \(\PageIndex{1}\): Which One Doesn't Belong: Arrows
Which pair of arrows doesn't belong?
1.
2.
3.
4.
Exercise \(\PageIndex{2}\): Warmer and Colder
1. Complete the table and draw a number line diagram for each situation.
| start (\(^{\circ}\)C) | change (\(^{\circ}\)C) | final (\(^{\circ}\)C) | addition equation | |
|---|---|---|---|---|
| a | \(+40\) | \(10\) degrees warmer | \(+50\) | \(40+10=50\) |
| b | \(+40\) | \(5\) degrees colder | ||
| c | \(+40\) | \(30\) degrees colder | ||
| d | \(+40\) | \(40\) degrees colder | ||
| e | \(+40\) | \(50\) degrees colder |
a.
b.
c.
d.
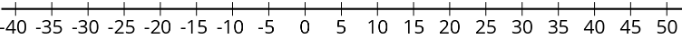
e.
2. Complete the table and draw a number line diagram for each situation.
| start (\(^{\circ}\)C) | change (\(^{\circ}\)C) | final (\(^{\circ}\)C) | addition equation | |
|---|---|---|---|---|
| a | \(-20\) | \(30\) degrees warmer | ||
| b | \(-20\) | \(35\) degrees warmer | ||
| c | \(-20\) | \(15\) degrees warmer | ||
| d | \(-20\) | \(15\) degrees colder |
a.
b.
c.
d.
Are you ready for more?
For the numbers \(a\) and \(b\) represented in the figure, which expression is equal to \(|a+b|\)?
\(|a|+|b|\qquad |a|-|b| \qquad |b|-|a|\)
Exercise \(\PageIndex{3}\): Winter Temperatures
One winter day, the temperature in Houston is \(8^{\circ}\) Celsius. Find the temperatures in these other cities. Explain or show your reasoning.
- In Orlando, it is \(10^{\circ}\) warmer than it is in Houston.
- In Salt Lake City, it is \(8^{\circ}\) colder than it is in Houston.
- In Minneapolis, it is \(20^{\circ}\) colder than it is in Houston.
- In Fairbanks, it is \(10^{\circ}\) colder than it is in Minneapolis.
- Use the thermometer applet to verify your answers and explore your own scenarios.
Summary
If it is \(42^{\circ}\) outside and the temperature increases by \(7^{\circ}\), then we can add the initial temperature and the change in temperature to find the final temperature.
\(42+7=49\)
If the temperature decreases by \(7^{\circ}\), we can either subtract \(42-7\) to find the final temperature, or we can think of the change as \(-7^{\circ}\). Again, we can add to find the final temperature.
\(42+(-7)=35\)
In general, we can represent a change in temperature with a positive number if it increases and a negative number if it decreases. Then we can find the final temperature by adding the initial temperature and the change. If it is \(3^{\circ}\) and the temperature decreases by \(7^{\circ}\), then we can add to find the final temperature.
\(3+(-7)=-4\)
We can represent signed numbers with arrows on a number line. We can represent positive numbers with arrows that start at 0 and points to the right. For example, this arrow represents +10 because it is 10 units long and it points to the right.
We can represent negative numbers with arrows that start at 0 and point to the left. For example, this arrow represents -4 because it is 4 units long and it points to the left.
To represent addition, we put the arrows “tip to tail.” So this diagram represents \(3+5\):
And this represents \(3+(-5)\):
Practice
Exercise \(\PageIndex{4}\)
- The temperature is \(-2^{\circ}\text{C}\). If the temperature rises by \(15^{\circ}\text{C}\), what is the new temperature?
- At midnight the temperature is \(-6^{\circ}\text{C}\). At midday the temperature is \(9^{\circ}\text{C}\). By how much did the temperature rise?
Exercise \(\PageIndex{5}\)
Draw a diagram to represent each of these situations. Then write an addition expression that represents the final temperature.
- The temperature was \(80^{\circ}\text{F}\) and then fell \(20^{\circ}\text{F}\).
- The temperature was \(-13^{\circ}\text{F}\) and then rose \(9^{\circ}\text{F}\).
- The temperature was \(-5^{\circ}\text{F}\) and then fell \(8^{\circ}\text{F}\).
Exercise \(\PageIndex{6}\)
Complete each statement with a number that makes the statement true.
- _____ < \(7^{\circ}\text{C}\)
- _____ < \(-3^{\circ}\text{C}\)
- \(-0.8^{\circ}\text{C}\) < _____ < \(-0.1^{\circ}\text{C}\)
- _____ > \(-2^{\circ}\text{C}\)
(From Unit 5.1.1)
Exercise \(\PageIndex{7}\)
Decide whether each table could represent a proportional relationship. If the relationship could be proportional, what would be the constant of proportionality?
- The number of wheels on a group of buses.
number of buses number of wheels wheels per bus \(5\) \(30\) \(8\) \(48\) \(10\) \(60\) \(15\) \(90\) Table \(\PageIndex{3}\) - The number of wheels on a train.
number of train cars number of wheels wheels per train car \(20\) \(184\) \(30\) \(264\) \(40\) \(344\) \(50\) \(424\) Table \(\PageIndex{4}\)
(From Unit 2.3.1)
Exercise \(\PageIndex{8}\)
Noah was assigned to make 64 cookies for the bake sale. He made 125% of that number. 90% of the cookies he made were sold. How many of Noah's cookies were left after the bake sale?
(From Unit 4.2.2)