7.3.4: Surface Area of Right Prisms

Lesson

Let's look at the surface area of prisms.

Exercise \(\PageIndex{1}\): Multifaceted

Your teacher will show you a prism.

1. What are some things you could measure about the object?
2. What units would you use for these measurements?

Exercise \(\PageIndex{2}\): So Many Faces

Here is a picture of your teacher's prism:

Figure \(\PageIndex{1}\)

Three students are trying to calculate the surface area of this prism.

• Noah says, “This is going to be a lot of work. We have to find the areas of 14 different faces and add them up.”
• Elena says, “It’s not so bad. All 12 rectangles are identical copies, so we can find the area for one of them, multiply that by 12 and then add on the areas of the 2 bases.”
• Andre says, “Wait, I see another way! Imagine unfolding the prism into a net. We can use 1 large rectangle instead of 12 smaller ones.”

1. Do you agree with any of them? Explain your reasoning.
2. How big is the “1 large rectangle” Andre is talking about? Explain or show your reasoning. If you get stuck, consider drawing a net for the prism.
3. Will Noah’s method always work for finding the surface area of any prism? Elena’s method? Andre’s method? Be prepared to explain your reasoning.
4. Which method do you prefer? Why?

Exercise \(\PageIndex{3}\): Revisiting a Pentagonal Prism

1. Between you and your partner, choose who will use each of these two methods to find the surface area of the prism.
   • Adding the areas of all the faces
   • Using the perimeter of the base.
2. Use your chosen method to calculate the surface area of the prism. Show your thinking. Organize it so it can be followed by others.

Figure \(\PageIndex{2}\)

3. Trade papers with your partner, and check their work. Discuss your thinking. If you disagree, work to reach an agreement.

Are you ready for more?

Figure \(\PageIndex{3}\)

Figure \(\PageIndex{4}\)

In a deck of cards, each card measures 6 cm by 9 cm.

1. When stacked, the deck is 2 cm tall, as shown in the first photo. Find the volume of this deck of cards.
2. Then the cards are fanned out, as shown in the second picture. The distance from the rightmost point on the bottom card to the rightmost point on the top card is now 7 cm instead of 2 cm. Find the volume of the new stack.

Summary

To find the surface area of a three-dimensional figure whose faces are made up of polygons, we can find the area of each face, and add them up!

Sometimes there are ways to simplify our work. For example, all of the faces of a cube with side length \(s\) are the same. We can find the area of one face, and multiply by 6. Since the area of one face of a cube is \(s^{2}\), the surface area of a cube is \(6s^{2}\).

We can use this technique to make it faster to find the surface area of any figure that has faces that are the same.

For prisms, there is another way. We can treat the prism as having three parts: two identical bases, and one long rectangle that has been taped along the edges of the bases. The rectangle has the same height as the prism, and its width is the perimeter of the base. To find the surface area, add the area of this rectangle to the areas of the two bases.

Glossary Entries

Definition: Base (of a prism or pyramid)

The word base can also refer to a face of a polyhedron.

A prism has two identical bases that are parallel. A pyramid has one base.

A prism or pyramid is named for the shape of its base.

Figure \(\PageIndex{5}\): The figure on the left is labeled pentagonal prism. There are two identical pentagons on the top and bottom. Each vertex of a pentagon is connected by a vertical segment to the corresponding vertex of the other pentagons. The pentagons are each shaded, with the word base pointing to each. The figure on the right is labeled hexagonal pyramid. There is a hexagon on the bottom shaded green. From a point above the hexagon extend 6 segments, each connected to a vertex of the hexagon.

Definition: Cross Section

A cross section is the new face you see when you slice through a three-dimensional figure.

For example, if you slice a rectangular pyramid parallel to the base, you get a smaller rectangle as the cross section.

Definition: Prism

A prism is a type of polyhedron that has two bases that are identical copies of each other. The bases are connected by rectangles or parallelograms.

Here are some drawings of prisms.

Figure \(\PageIndex{6}\)

Definition: Pyramid

A pyramid is a type of polyhedron that has one base. All the other faces are triangles, and they all meet at a single vertex.

Here are some drawings of pyramids.

Figure \(\PageIndex{7}\)

Definition: Surface Area

The surface area of a polyhedron is the number of square units that covers all the faces of the polyhedron, without any gaps or overlaps.

For example, if the faces of a cube each have an area of 9 cm², then the surface area of the cube is \(6\cdot 9\), or 54 cm².

Definition: Volume

Volume is the number of cubic units that fill a three-dimensional region, without any gaps or overlaps.

For example, the volume of this rectangular prism is 60 units³, because it is composed of 3 layers that are each 20 units³.

Figure \(\PageIndex{8}\)

Practice

Exercise \(\PageIndex{4}\)

Edge lengths are given in units. Find the surface area of each prism in square units.

Figure \(\PageIndex{9}\): Five prisms. Prism A, rectangular prism with dimensions 5, 8, 10. Prism B, base is a right triangle with sides 6, 8, 10, prism height 15. Prism C, rectangular prism with dimensions 5, 13, 4. Prism D, base is a right triangle with sides 5, 12, and 13, prism height is 8. Prism E, base is a triangle with sides 6, 5, 5 and height perpendicular to the 6 side is 4, prism height 12.

Exercise \(\PageIndex{5}\)

Priya says, “No matter which way you slice this rectangular prism, the cross section will be a rectangle.” Mai says, “I’m not so sure.” Describe a slice that Mai might be thinking of.

Figure \(\PageIndex{10}\)

(From Unit 7.3.1)

Exercise \(\PageIndex{6}\)

\(B\) is the intersection of line \(AC\) and line \(ED\). Find the measure of each of the angles.

Figure \(\PageIndex{11}\): Two lines and two rays that intersect at point B creating 6 angles. Line AC is slanted downward and to the right and line ED is slanted upward and to the right. Ray BG is drawn between line segment BD and line segment BC. Angle GBC that is formed measures 65 degrees. Ray BF is drawn between line segment BC and line segment BE. Angle FBE that is formed measures 20 degrees. Angle ABE is labeled 110 degrees.

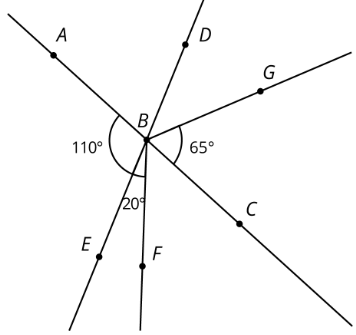
1. Angle \(ABF\)
2. Angle \(ABD\)
3. Angle \(EBC\)
4. Angle \(FBC\)
5. Angle \(DBG\)

(From Unit 7.1.5)

Exercise \(\PageIndex{7}\)

Write each expression with fewer terms.

1. \(12m-4m\)
2. \(12m-5k+m\)
3. \(9m+k-(3m-2k)\)

(From Unit 6.4.3)

Exercise \(\PageIndex{8}\)

1. Find 44% of 625 using the facts that 40% of 625 is 250 and 4% of 625 is 25.
2. What is 4.4% of 625?
3. What is 0.44% of 625?

(From Unit 4.2.4)