5.2: Introduction to Decimals
- Page ID
- 22488
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Recall that whole numbers are constructed by using digits.
The set
\[ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} \nonumber\nonumber \]
is called the set of digits.
As an example, the whole number 55,555 (“fifty-five thousand five hundred fifty-five”) is constructed by using a single digit. However, the position of the digit 5 determines its value in the number 55,555. The first occurrence of the
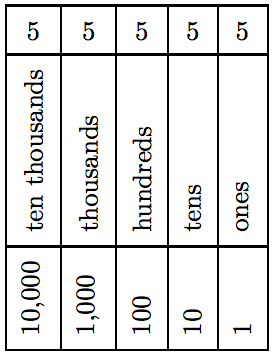
Table 5.1: Place value.
digit 5 happens in the ten thousands place, so its value is 5 ten thousands, or 50,000. The next occurrence of the digit 5 is in the thousands place, so its value is 5 thousands, or 5,000. Indeed, the whole number 55,555 in expanded form is
50000 + 5000 + 500 + 50 + 5,
which reflects the value of the digit 5 in each place.
Decimal Notation
In Table 5.1, each time you move one column to the left, the place value is 10 times larger than the place value of the preceding column. Vice-versa, each time you move one column to the right, the place value is 1/10 of the place value of the preceding column.
Now, consider the decimal number 12.3456, which consists of three parts: the whole number part, the decimal point, and the fractional part.
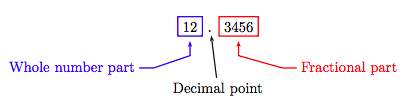
The whole number part of the decimal number is the part that lies strictly to the left of the decimal point, and the place value of each digit in the whole number part is given by the columns shown in Table 5.1.
The fractional part of the decimal number is the part that lies strictly to the right of the decimal point. As we saw in Table 5.1, each column has a value equal to 1/10 of the value of the column that lies to its immediate left. Thus, it should come as no surprise that:
- The first column to the right of the decimal point has place value 1/10 (tenths).
- The second column to the right of the decimal point has place value 1/100 (hundredths).
- The third column to the right of the decimal point has place value 1/1000 (thousandths).
- The fourth column to the right of the decimal point has place value 1/10000 (ten-thousandths).
These results are summarized for the decimal number 12.3456 in Table 5.2.
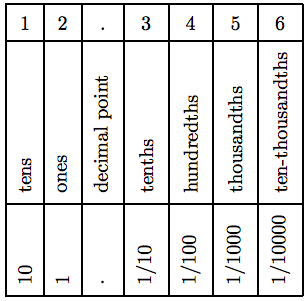
Table 5.2: Place value.
Pronouncing Decimal Numbers
The decimal number 12.3456 is made up of 1 ten, 2 ones, 3 tenths, 4 hundredths, 5 thousandths, and 6 ten-thousandths (see Table 5.2), and can be written in expanded form as
\[12.3456 = 10 + 2 + \frac{3}{10} + \frac{4}{100} + \frac{5}{1000} + \frac{6}{10000}.\nonumber \]
Note that the whole numbers can be combined and the fractions can be written with a common denominator and summed.
\[ \begin{aligned} 12.3456 & = 12 + \frac{3 \cdot \textcolor{red}{1000}}{10 \cdot \textcolor{red}{1000}} + \frac{4 \cdot \textcolor{red}{100}}{100 \cdot \textcolor{red}{100}} + \frac{5 \cdot \textcolor{red}{10}}{1000 \cdot \textcolor{10}} + \frac{6}{10000} \\ & = 12 + \frac{3000}{10000} + \frac{400}{10000} + \frac{50}{10000} + \frac{6}{10000} \\ & = 12 + \frac{3456}{10000} \end{aligned}\nonumber \]
The result tells us how to pronounce the number 12.3456. It is pronounced “twelve and three thousand, four hundred fifty-six ten-thousandths.”
Place the decimal number 1,234.56 in expanded form, then combine the whole number part and sum the fractional part over a common denominator. Use the result to help pronounce the decimal number.
Solution
In expanded form,
\[1, 234.56 = 1, 000 + 200 + 30 + 4 + \frac{5}{10} + \frac{6}{100}\nonumber \]
Sum the whole number parts. Express the fractional parts as equivalent fractions and combine over one common denominator.
\[ \begin{aligned} = 1,234 + \frac{5 \cdot \textcolor{10}}{10 \cdot \textcolor{red}{10}} + \frac{6}{100} \\ = 1,234 + \frac{50}{100} + \frac{6}{100} \\ = 1, 234 + \frac{56}{100} \end{aligned} \nonumber \]
Hence, 1,234.56 is pronounced “one thousand, two hundred thirty-four and fifty-six hundreths."
Place the decimal number 3,502.23 in expanded form, then combine the whole number part and sum the fractional part over a common denominator.
- Answer
-
\(3,502 + \frac{23}{100}\)
Place the decimal number 56.128 in expanded form, then combine the whole number part and sum the fractional part over a common denominator. Use the result to help pronounce the decimal number.
Solution
In expanded form,
\[56.128 = 50 + 6 + \frac{1}{10} + \frac{2}{100} + \frac{8}{1000}\nonumber \]
Sum the whole number parts. Express the fractional parts as equivalent fractions and combine over one common denominator.
\[ \begin{aligned} = 56 + \frac{1 \cdot \textcolor{red}{100}}{10 \cdot \textcolor{red}{100}} + \frac{2 \cdot \textcolor{red}{10}}{100 \cdot \textcolor{red}{10}} + \frac{8}{1000} \\ = 56 + \frac{100}{1000} + \frac{20}{1000} + \frac{8}{1000} \\ = 56 + \frac{128}{1000} \end{aligned}\nonumber \]
Thus, 56.128 is pronounced “fifty-six and one hundred twenty-eight thousandths.”
Place the decimal number 235.568 in expanded form, then combine the whole number part and sum the fractional part over a common denominator.
- Answer
-
\(235 + \frac{568}{1000}\)
The discussion and example leads to the following result.
- Pronounce the whole number part to the left of the decimal as you would any whole number.
- Say the word “and” for the decimal point.
- State the fractional part to the right of the decimal as you would any whole number, followed by the place value of the digit in the rightmost column.
Pronounce the decimal number 34.12.
Solution
The rightmost digit in the fractional part of 34.12 is in the hundredths column. Thus, 34.12 is pronounced “thirty-four and twelve hundredths.”
Pronounce 28.73
- Answer
-
“Twenty-eight and seventy-three hundredths”
In pronouncing decimal numbers, the decimal point is read as “and.” No other instance of the word “and” should appear in the pronunciation.
Explain why “four hundred and thirty-four and two tenths” is an incorrect pronunciation of the decimal number 434.2.
Solution
The decimal point is read as “and.” No other occurrence of the word “and” is allowed in the pronunciation. The correct pronunciation should be “four hundred thirty-four and two tenths.”
Pronounce 286.9.
- Answer
-
"Two hundred eighty six and nine tenths"
Pronounce the decimal number 5,678.123.
Solution
The rightmost digit in the fractional part of 5,678.123 is in the thousandths column. Hence, 5,678.123 is pronounced “five thousand six hundred seventy-eight and one hundred twenty-three thousandths.”
Pronounce 7, 002.207
- Answer
-
Answer: “Seven thousand two and two hundred seven thousandths.”
Pronounce the decimal number 995.4325.
Solution
The rightmost digit in the fractional part of 995.4325 is in the ten-thousandths column. Hence, 995.4325 is pronounced “nine hundred ninety-five and four thousand three hundred twenty-five ten-thoudandths.”
Pronounce 500.1205.
- Answer
-
Answer: “Five hundred and one thousand two hundred five ten-thousandths.”
Decimals to Fractions
Because we now have the ability to pronounce decimal numbers, it is a simple exercise to change a decimal to a fraction.1 For example, 134.12 is pronounced “one hundred thirty-four and twelve hundredths,” so it can easily be written as a mixed fraction.
\[134.12 = 134 \frac{12}{100}\nonumber \]
But this mixed fraction can be changed to an improper fraction.
\[ \begin{aligned} 134 \frac{12}{100} \\ & = \frac{100 \cdot 134 + 12}{100} & = \frac{13400 + 12}{100} \\ * = \frac{13412}{100} \end{aligned}\nonumber \]
Note that the numerator is our original number without the decimal point. There are two decimal places in the original number and the denominator of the final improper fraction contains two zeros.
This discussion leads to the following result.
1Changing fractions to decimals will be covered in Section 5.5.
To change a decimal number to an improper fraction, proceed as follows:
- Create a fraction.
- Place the decimal number in the numerator without the decimal point.
- Count the number of decimal places. Place an equal number of zeros in the denominator.
Change the following decimal numbers to improper fractions: (a) 1.2345, and (b) 27.198.
Solution
In each case, place the number in the numerator without the decimal point. In the denominator, add a number of zeros equal to the number of decimal places.
a) The decimal number 1.2345 has four decimal places. Hence,
\[1.2345 = \frac{12345}{10000}\nonumber \]
b) The decimal number 27.198 has three decimal places. Hence,
\[27.198 = \frac{27198}{1000}\nonumber \]
Change 17.205 to an improper fraction.
- Answer
-
\(\frac{17205}{100}\)
Change each of the following decimals to fractions reduced to lowest terms: (a) 0.35, and (b) 0.125.
Solution
Place each number in the numerator without the decimal point. Place a number of zeros in the denominator equal to the number of decimal places. Reduce to lowest terms.
a) First, place 35 over 100.
\[0.35 = \frac{35}{100}\nonumber \]
We can divide both numerator and denominator by the greatest common divisor.
\[ \begin{aligned} = \frac{35 \div 5}{100 \div 5} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by 5.}} \\ = \frac{7}{20} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
b) First, place 125 over 1000.
\[0.125 = \frac{125}{1000}\nonumber \]
Prime factor and cancel common factors.
\[ \begin{aligned} = \frac{5 \cdot 5 \cdot 5}{2 \cdot 2 \cdot 2 \cdot 5 \cdot 5 \cdot 5} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = \frac{ \cancel{5} \cdot \cancel{5} \cdot \cancel{5}}{2 \cdot 2 \cdot 2 \cdot \cancel{5} \cdot \cancel{5} \cdot \cancel{5}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{1}{8} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Change 0.375 to a fraction, reduced to lowest terms.
- Answer
-
3/8
Rounding
The rules for rounding decimal numbers are almost identical to the rules for rounding whole numbers. First, a bit of terminology.
The digit in the place to which we wish to round is called the rounding digit and the digit that follows on its immediate right is called the test digit.
If we want to round the decimal number 12.254 to the nearest hundredth, then the rounding digit is 5 and the test digit is 4.
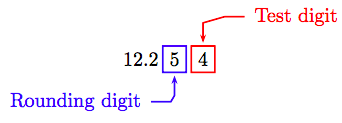
If we used the rules for rounding whole numbers, because the test digit 4 is less than 5, we would replace all digits to the right of the rounding digit with zeros to obtain the following approximation.
12.254 ≈ 12.250
However, because
\[12.250 = 12 \frac{250}{1000} = 12 \frac{25}{100},\nonumber \]
the trailing zero at the end of the fractional part is irrelevant. Hence, we truncate every digit after the rounding digit and use the following approximation.
12.254 ≈ 12.25
Deleting trailing zeros from the end of the fractional part of a decimal number does not change its value.
The above discussion motivates the following algorithm for rounding decimal numbers.
Locate the rounding digit and the test digit.
- If the test digit is greater than or equal to 5, add 1 to the rounding digit and truncate all digits to the right of the rounding digit.
- If the test digit is less than 5, simply truncate all digits to the right of the rounding digit.
Round 8.7463 to the nearest hundredth.
Solution
Locate the rounding digit in the hundredths place and the test digit to its immediate right.
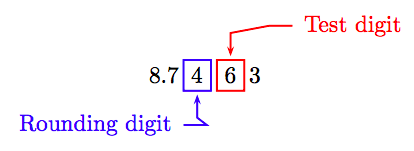
Because the test digit is greater than 5, add 1 to the rounding digit and truncate all digits to the right of the rounding digit. Hence, to the nearest hundredth:
8.7463 ≈ 8.75
Round 9.2768 to the nearest hundredth.
- Answer
-
9.28
Round 113.246 to the nearest tenth.
Solution
Locate the rounding digit in the tenths place and the test digit to its immediate right.
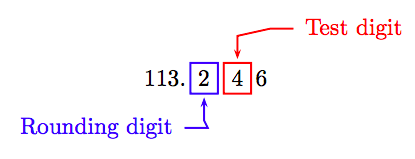
Because the test digit is less than 5, truncate all digits to the right of the rounding digit. Hence, to the nearest tenth:
113.246 ≈ 113.2
Round 58.748 to the nearest tenth.
- Answer
-
58.7
Comparing Decimals
We can compare two positive decimals by comparing digits in each place as we move from left to right, place by place. For example, suppose we wish to compare the decimal numbers 5.234 and 5.2357. First, add enough trailing zeros to the decimal number with the fewer decimal places so that the numbers have the same number of decimal places. In this case, note that
\[ 5.234 = 5 \frac{234}{1000} = 5 \frac{2340}{10000} = 5.2340.\nonumber \]
Adding trailing zeros to the end of the fractional part of a decimal number does not change its value.
Next, align the numbers as follows.
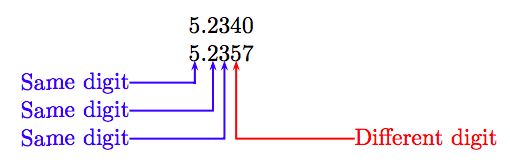
As you scan the columns, moving left to right, the first place that has different digits occurs in the thousandths place, where the digit 5 is the second number is greater than the digit 4 in the first number in the same place. Because 5 is greater than 4, the second number is larger than the first. That is:
5.234 < 5.2357
This discussion suggests the following algorithm.
- Add enough trailing zeros so that both numbers have the same number of decimal places.
- Compare the digits in each place, moving left to right.
- As soon as you find two digits in the same place that are different, the decimal number with the greatest digit in this place is the larger number.
Compare 4.25 and 4.227.
Solution
Add a trailing zero to the first decimal number and align the numbers as follows.
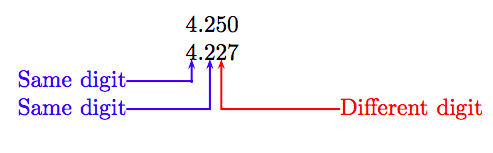
The first difference is in the hundredths place, where the digit 5 in the first number is greater than the digit 2 in the same place of the second number. Hence, the first number is larger than the second; that is:
4.25 > 4.227
Compare 8.34 and 8.348.
- Answer
-
8.34 < 8.348
When comparing negative numbers, the number with the larger magnitude is the smaller number. Hence, we have to adjust our algorithm for comparing negative decimal numbers.
- Add enough trailing zeros so that both numbers have the same number of decimal places.
- Compare the digits in each place, moving left to right.
- As soon as you find two digits in the same place that are different, the decimal number with the greatest digit in this place is the smaller number.
Compare −4.25 and −4.227.
Solution
Add a trailing zero to the first decimal number and align the numbers as follows.
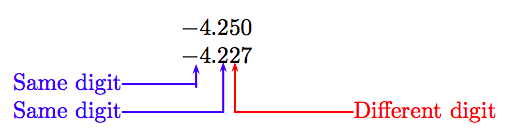
The first difference is in the hundredths place, where the digit 5 in the first number is greater than the digit 2 in the same place of the second number. Hence, the first number is smaller than the second; that is:
−4.25 < −4.227
Compare −7.86 and −7.85.
- Answer
-
−7.86 < −7.85
Exercises
1. Which digit is in the tenths column of the number 4,552.0908?
2. Which digit is in the thousandths column of the number 7,881.6127?
3. Which digit is in the tenths column of the number 4,408.2148?
4. Which digit is in the tenths column of the number 9,279.0075?
5. Which digit is in the ten-thousandths column of the number 2,709.5097?
6. Which digit is in the hundredths column of the number 1,743.1634?
7. Which digit is in the hundredths column of the number 3,501.4456?
8. Which digit is in the ten-thousandths column of the number 9,214.3625?
9. Which digit is in the hundredths column of the number 5,705.2193?
10. Which digit is in the hundredths column of the number 7,135.2755?
11. Which digit is in the tenths column of the number 8,129.3075?
12. Which digit is in the thousandths column of the number 6,971.4289?
In Exercises 13-20, write the given decimal number in expanded form.
13. 46.139
14. 68.392
15. 643.19
16. 815.64
17. 14.829
18. 45.913
19. 658.71
20. 619.38
In Exercises 21-28, follow the procedure shown in Examples 1 and 2 to write the decimal number in expanded form, then combine the whole number part and sum the fractional part over a common denominator.
21. 32.187
22. 35.491
23. 36.754
24. 89.357
25. 596.71
26. 754.23
27. 527.49
28. 496.15
In Exercises 29-40, pronounce the given decimal number. Write your answer out in words.
29. 0.9837
30. 0.6879
31. 0.2653
32. 0.8934
33. 925.47
34. 974.35
35. 83.427
36. 32.759
37. 63.729
38. 85.327
39. 826.57
40. 384.72
In Exercises 41-52, convert the given decimal to a mixed fraction. Do not simplify your answer.
41. 98.1
42. 625.591
43. 781.7
44. 219.999
45. 915.239
46. 676.037
47. 560.453
48. 710.9
49. 414.939
50. 120.58
51. 446.73
52. 653.877
In Exercises 53-60, convert the given decimal to an improper fraction. Do not simplify your answer.
53. 8.7
54. 3.1
55. 5.47
56. 5.27
57. 2.133
58. 2.893
59. 3.9
60. 1.271
In Exercises 61-68, convert the given decimal to a fraction. Reduce your answer to lowest terms.
61. 0.35
62. 0.38
63. 0.06
64. 0.84
65. 0.98
66. 0.88
67. 0.72
68. 0.78
69. Round 79.369 to the nearest hundredth.
70. Round 54.797 to the nearest hundredth.
71. Round 71.2427 to the nearest thousandth.
72. Round 59.2125 to the nearest thousandth.
73. Round 29.379 to the nearest tenth.
74. Round 42.841 to the nearest tenth.
75. Round 89.3033 to the nearest thousandth.
76. Round 9.0052 to the nearest thousandth.
77. Round 20.655 to the nearest tenth.
78. Round 53.967 to the nearest tenth.
79. Round 19.854 to the nearest hundredth.
80. Round 49.397 to the nearest hundredth.
In Exercises 81-92, determine which of the two given statements is true.
81. 0.30387617 < 0.3036562 or 0.30387617 > 0.3036562
82. 8.5934 < 8.554 or 8.5934 > 8.554
83. −0.034 < −0.040493 or −0.034 > −0.040493
84. −0.081284 < −0.08118 or −0.081284 > −0.08118
85. −8.3527 < −8.36553 or −8.3527 > −8.36553
86. −0.00786 < −0.0051385 or −0.00786 > −0.0051385
87. 18.62192 < 18.6293549 or 18.62192 > 18.6293549
88. 514.873553 < 514.86374 or 514.873553 > 514.86374
89. 36.8298 < 36.8266595 or 36.8298 > 36.8266595
90. 0.000681 < 0.00043174 or 0.000681 > 0.00043174
91. −15.188392 < −15.187157 or −15.188392 > −15.187157
92. −0.049785 < −0.012916 or −0.049785 > −0.012916
93. Write the decimal number in words.
i) A recently discovered 7.03-carat blue diamond auctioned at Sotheby’s.
ii) The newly launched European Planck telescope will stay in orbit 1.75 years measuring radiation from the Big Bang.
iii) The sun composes 0.9985 of the mass in our solar system.
iv) Clay particles are small - only 0.0001 inch.
94. Light speed. The index of refraction for a given material is a value representing the number of times slower a light wave travels in that particular material than it travels in the vacuum of space.
i) Reorder the materials by their index of refraction from lowest to highest.
ii) How many times slower is a lightwave in a diamond compared with a vacuum?
| Material | Index of Refraction |
| Diamond | 2.417 |
| Vacuum | 1.0000 |
| Plexiglass | 1.51 |
| Air | 1.0003 |
| Water | 1.333 |
| Zircon | 1.923 |
| Crown Glass | 1.52 |
| Ice | 1.31 |
95. Shorter day? Scientists at NASA’s Jet Propulsion Laboratory calculated that the earthquake in Chile may have shortened the length of a day on Earth by 1.26 millionths of a second.
i) Write that number completely as a decimal.
ii) Actual observations of the length of the day are accurate to five millionths of a second. Write this fraction as a decimal.
iii) Comparing the two decimals above and determine which is smaller. Do you think scientists can observe and measure the calculated slowing of the earth?
Answers
1. 0
3. 2
5. 7
7. 4
9. 1
11. 3
13. \(40 + 6 + 1 10 + \frac{3}{100} + \frac{9}{1000}\)
15. \(600 + 40 + 3 + \frac{1}{10} + \frac{9}{100}\)
17. \(10 + 4 + \frac{8}{10} + \frac{2}{100} + \frac{9}{1000}\)
19. \(600 + 50 + 8 + \frac{7}{10} + \frac{1}{100}\)
21. \(32 + \frac{187}{1000}\)
23. \(36 + \frac{754}{1000}\)
25. \(596 + \frac{71}{100}\)
27. \(527 + \frac{49}{100}\)
29. nine thousand eight hundred thirty-seven ten-thousandths
31. two thousand six hundred fifty-three ten-thousandths
33. nine hundred twenty-five and forty-seven hundredths
35. eighty-three and four hundred twenty-seven thousandths
37. sixty-three and seven hundred twenty-nine thousandths
39. eight hundred twenty-six and fifty-seven hundredths
41. \(98 \frac{1}{10}\)
43. \(781 \frac{7}{10}\)
45. \(915 \frac{239}{1000}\)
47. \(560 \frac{453}{1000}\)
49. \(414 \frac{939}{1000}\)
51. \(446 \frac{73}{100}\)
53. \(\frac{87}{10}\)
55. \(\frac{547}{100}\)
57. \(\frac{2133}{1000}\)
59. \(\frac{39}{10}|)
61. \(\frac{7}{20}\)
63. \(\frac{3}{50}\)
65. \(\frac{49}{50}|)
67. \(\frac{18}{25}\)
69. 79.37
71. 71.243
73. 29.4
75. 89.303
77. 20.7
79. 19.85
81. 0.30387617 > 0.3036562
83. −0.034 > −0.040493
85. −8.3527 > −8.36553
87. 18.62192 < 18.6293549
89. 36.8298 > 36.8266595
91. −15.188392 < −15.187157
93.
i) seven and three hundredths
ii) one and seventy-five hundredths
iii) nine thousand nine hundred eighty-five ten-thousandths
iv) one ten-thousandth of an inch
95.
i) 0.00000126
ii) 0.000005
iii) 0.00000126 < 0.000005; scientists would be unable to measure the calculated change in the length of a day.


