5.9: The Pythagorean Theorem
- Page ID
- 24413
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Pythagoras was a Greek mathematician and philosopher, born on the island of Samos (ca. 582 BC). He founded a number of schools, one in particular in a town in southern Italy called Crotone, whose members eventually became known as the Pythagoreans. The inner circle at the school, the Mathematikoi, lived at the school, rid themselves of all personal possessions, were vegetarians, and observed a strict vow of silence. They studied mathematics, philosophy, and music, and held the belief that numbers constitute the true nature of things, giving numbers a mystical or even spiritual quality.
Today, nothing is known of Pythagoras’s writings, perhaps due to the secrecy and silence of the Pythagorean society. However, one of the most famous theorems in all of mathematics does bear his name, the Pythagorean Theorem.
Prior to revealing the contents of the Pythagorean Theorem, we pause to provide the definition of a right triangle and its constituent parts.
A triangle with one right angle (90◦) is called a right triangle. In the figure below, the right angle is marked with a little square.
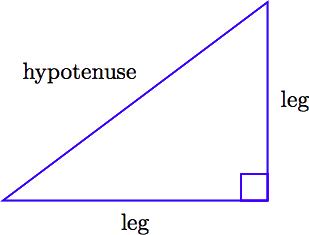
The side of the triangle that is directly opposite the right angle is called the hypotenuse. The sides of the triangle that include the right angle are called the legs of the right triangle.
Now we can state one of the most ancient theorems of mathematics, the Pythagorean Theorem.
Let \(c\) represent the length of the hypotenuse of a right triangle, and let a and b represent the lengths of its legs, as pictured in the image that follows.
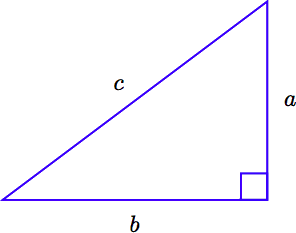
The relationship involving the legs and hypotenuse of the right triangle, given by
\[a^2 + b^2 = c^2,\nonumber \]
is called the Pythagorean Theorem.
Here are two important observations.
Two important facts regarding the hypotenuse of the right triangle are:
- The hypotenuse is the longest side of the triangle and lies directly opposite the right angle.
- In the Pythagorean equation \(a^2 + b^2 = c^2\), the hypotenuse lies by itself on one side of the equation.
The Pythagorean Theorem can only be applied to right triangles.
Let’s look at a simple application of the Pythagorean Theorem.
The legs of a right triangle measure 3 and 4 meters, respectively. Find the length of the hypotenuse.
Solution
Let’s follow the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. Let c represent the length of the hypotenuse, as pictured in the following sketch.
2. Set up an Equation. The Pythagorean Theorem says that
\[a^2 + b^2 = c^2.\nonumber \]
In this example, the legs are known. Substitute 4 for a and 3 for b (3 for a and 4 for b works equally well) into the Pythagorean equation.
\[4^2 + 3^2 = c^2\nonumber \]
3. Solve the Equation.
\[ \begin{aligned} 4^2 + 3^2 = c^2 ~ & \textcolor{red}{ \text{ The Pythagorean equation.}} \\ 16 + 9 = c^2 ~ & \textcolor{red}{ \text{ Exponents first: } 4^2 = 16 \text{ and } 3^2 = 9.} \\ 25 = c^2 ~ & \textcolor{red}{ \text{ Add: } 16+9=25.} \\ 5 = c~ & \textcolor{red}{ \text{ Take the nonnegative square root.}} \end{aligned}\nonumber \]
Technically, there are two answers to c2 = 25, i.e., c = −5 or c = 5. However, c represents the hypotenuse of the right triangle and must be nonnegative. Hence, we must choose c = 5.
4. Answer the Question. The hypotenuse has length 5 meters.
5. Look Back. Do the numbers satisfy the Pythagorean Theorem? The sum of the squares of the legs should equal the square of the hypotenuse. Let’s check.
\[\begin{aligned} 4^2 + 3^2 = 5^2 \\ 16 + 9 = 25 \\ 25 = 25 \end{aligned}\nonumber \]
All is well!
The legs of a right triangle measure 5 and 12 feet, respectively. Find the length of the hypotenuse.
- Answer
-
13 feet
Given the following right triangle, find the length of the missing side.
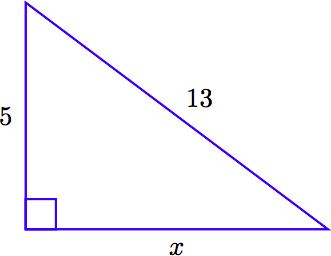
Solution
Note that the hypotenuse (across from the right angle) has length 13. This quantity should lie on one side of the Pythagorean equation all by itself. The sum of the squares of the legs go on the other side. Hence,
\[5^2 + x^2 = 13^2\nonumber \]
Solve the equation for x.
\[ \begin{aligned} 25+x^2 = 169 ~ & \textcolor{red}{ \text{ Exponents first: } 5^2 = 25 \text{ and } 13^2 = 169.} \\ 25 + x^2 -25 = 169 - 25 ~ & \textcolor{red}{ \text{ Subtract 25 from both sides.}} \\ x^2 = 144 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ x= 12 ~ & \textcolor{red}{ \text{ Take the nonnegative square root of 144.}} \end{aligned}\nonumber \]
The hypotenuse of a right triangle measures 25 centimeters. One leg of the right triangle measures 24 centimeters. Find the length of the remaining leg.
- Answer
-
7 centimeters
Perfect squares are nice, but not required.
Given the following right triangle, find the exact length of the missing side.
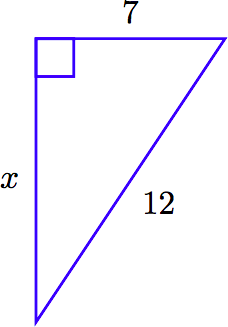
Solution
Note that the hypotenuse (across from the right angle) has length 12. This quantity should lie on one side of the Pythagorean equation all by itself. The sum of the squares of the legs go on the other side. Hence,
\[x^2 + 7^2 = 12^2\nonumber \]
Solve the equation for x.
\[ \begin{aligned} x^2 + 49 = 144 ~ & \textcolor{red}{ \text{ Exponents first: } 7^2 = 49 \text{ and } 12^2 = 144.} \\ x^2 + 49-49 = 144 - 49 ~ & \textcolor{red}{ \text{ Subtract 49 from both sides.}} \\ x^2 = 95 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ x = \sqrt{95} ~ & \textcolor{red}{ \text{ Take the nonnegative square root of 95.}} \end{aligned}\nonumber \]
Hence, the exact length of the missing side is \(\sqrt{95}\).
The hypotenuse and one leg of a right triangle measure 9 and 7 inches, respectively. Find the length of the remaining leg.
- Answer
-
Add texts here. Do not delete this text first.
Any attempt to use your calculator to approximate 95 in Example 3 would be an error as the instructions asked for an exact answer.
Sometimes an approximate answer is desired, particularly in applications.
Ginny want to create a vegetable garden in the corner of her yard in the shape of a right triangle. She cuts two boards of length 8 feet which will form the legs of her garden. Find the length of board she should cut to form the hypotenuse of her garden, correct to the nearest tenth of a foot.
Solution
We follow the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. We begin with a labeled sketch. Let x represent the length of the unknown hypotenuse.
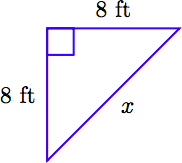
2. Set Up an Equation. The hypotenuse is isolated on one side of the Pythagorean equation.
\[x^2 = 8^2 + 8^2\nonumber \]
3. Solve the Equation.
\[ \begin{aligned} x^2 = 8^2 + 8^2 ~ & \textcolor{red}{ \text{ The Pythagorean equation.}} \\ x^2 = 64 + 64 ~ & \textcolor{red}{ \text{ Exponents first: } 8^2 = 64 \text{ and } 8^2 = 64.} \\ x^2 = 128 ~ & \textcolor{red}{ \text{ Add: } 64 + 64 = 128.} \\ x = \sqrt{128} ~ & \textcolor{red}{ \text{ Take the nonnegative square root.}} \end{aligned}\nonumber \]
4. Answer the Question. The exact length of the hypotenuse is \(\sqrt{128}\) feet, but we’re asked to find the hypotenuse to the nearest tenth of a foot. Using a calculator, we find an approximation for \(\sqrt{128}\).
\[\sqrt{128} \approx 11.313708499\nonumber \]
To round to the nearest tenth, first identify the rounding and test digits.
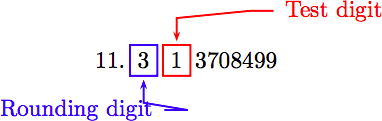
The test digit is less than five. So we leave the rounding digit alone and truncate. Therefore, correct to the nearest tenth of a foot, the length of the hypotenuse is approximately 11.3 feet.
5. Look Back. The sum of the squares of the legs is
\[ \begin{aligned} 8^2 + 8^2 = 64 + 64 \\ = 128. \end{aligned}\nonumber \]
The square of the hypotenuse is
\[(11.3)^2 = 127.69\nonumber \]
These are almost the same, the discrepancy due to the fact that we rounded to find an approximation for the hypotenuse.
A 15 foot ladder leans against the wall of a building. The base of the ladder lies 5 feet from the base of the wall. How high up the wall does the top of the ladder reach? Round your answer to the nearest tenth of a foot.
- Answer
-
14.1 feet
Exercises
In Exercises 1-16, your solutions should include a well-labeled sketch.
1. The length of one leg of a right triangle is 15 meters, and the length of the hypotenuse is 25 meters. Find the exact length of the other leg.
2. The length of one leg of a right triangle is 7 meters, and the length of the hypotenuse is 25 meters. Find the exact length of the other leg.
3. The lengths of two legs of a right triangle are 12 meters and 16 meters. Find the exact length of the hypotenuse.
4. The lengths of two legs of a right triangle are 9 meters and 12 meters. Find the exact length of the hypotenuse.
5. The length of one leg of a right triangle is 13 meters, and the length of the hypotenuse is 22 meters. Find the exact length of the other leg.
6. The length of one leg of a right triangle is 6 meters, and the length of the hypotenuse is 15 meters. Find the exact length of the other leg.
7. The lengths of two legs of a right triangle are 2 meters and 21 meters. Find the exact length of the hypotenuse.
8. The lengths of two legs of a right triangle are 7 meters and 8 meters. Find the exact length of the hypotenuse.
9. The length of one leg of a right triangle is 12 meters, and the length of the hypotenuse is 19 meters. Find the exact length of the other leg.
10. The length of one leg of a right triangle is 5 meters, and the length of the hypotenuse is 10 meters. Find the exact length of the other leg.
11. The lengths of two legs of a right triangle are 6 meters and 8 meters. Find the exact length of the hypotenuse.
12. The lengths of two legs of a right triangle are 5 meters and 12 meters. Find the exact length of the hypotenuse.
13. The length of one leg of a right triangle is 6 meters, and the length of the hypotenuse is 10 meters. Find the exact length of the other leg.
14. The length of one leg of a right triangle is 9 meters, and the length of the hypotenuse is 15 meters. Find the exact length of the other leg.
15. The lengths of two legs of a right triangle are 6 meters and 22 meters. Find the exact length of the hypotenuse.
16. The lengths of two legs of a right triangle are 9 meters and 19 meters. Find the exact length of the hypotenuse.
In Exercises 17-24, your solutions should include a well-labeled sketch.
17. The lengths of two legs of a right triangle are 3 meters and 18 meters. Find the length of the hypotenuse. Round your answer to the nearest hundredth.
18. The lengths of two legs of a right triangle are 10 feet and 16 feet. Find the length of the hypotenuse. Round your answer to the nearest tenth.
19. The length of one leg of a right triangle is 2 meters, and the length of the hypotenuse is 17 meters. Find the length of the other leg. Round your answer to the nearest tenth.
20. The length of one leg of a right triangle is 4 meters, and the length of the hypotenuse is 12 meters. Find the length of the other leg. Round your answer to the nearest hundredth.
21. The lengths of two legs of a right triangle are 15 feet and 18 feet. Find the length of the hypotenuse. Round your answer to the nearest hundredth.
22. The lengths of two legs of a right triangle are 6 feet and 13 feet. Find the length of the hypotenuse. Round your answer to the nearest tenth.
23. The length of one leg of a right triangle is 4 meters, and the length of the hypotenuse is 8 meters. Find the length of the other leg. Round your answer to the nearest hundredth.
24. The length of one leg of a right triangle is 3 meters, and the length of the hypotenuse is 15 meters. Find the length of the other leg. Round your answer to the nearest tenth.
25. Greta and Fritz are planting a 13-meter by 18-meter rectangular garden, and are laying it out using string. They would like to know the length of a diagonal to make sure that right angles are formed. Find the length of a diagonal. Round your answer to the nearest hundredth. Your solution should include a well-labeled sketch.
26. Markos and Angelina are planting an 11- meter by 19-meter rectangular garden, and are laying it out using string. They would like to know the length of a diagonal to make sure that right angles are formed. Find the length of a diagonal. Round your answer to the nearest tenth. Your solution should include a well-labeled sketch.
27. The base of a 24-meter long guy wire is located 10 meters from the base of the telephone pole that it is anchoring. How high up the pole does the guy wire reach? Round your answer to the nearest hundredth. Your solution should include a well-labeled sketch.
28. The base of a 30-foot long guy wire is located 9 feet from the base of the telephone pole that it is anchoring. How high up the pole does the guy wire reach? Round your answer to the nearest hundredth. Your solution should include a well-labeled sketch.
29. Hiking Trail. A hiking trail runs due south for 8 kilometers, then turns west for about 15 kilometers, and then heads northeast on a direct path to the starting point. How long is the entire trail?
30. Animal Trail. An animal trail runs due east from a watering hole for 12 kilometers, then goes north for 5 kilometers. Then the trail turns southwest on a direct path back to the watering hole. How long is the entire trail?
31. Upper Window. A 10-foot ladder leans against the wall of a house. How close to the wall must the bottom of the ladder be in order to reach a window 8 feet above the ground?
32. How high? A 10-foot ladder leans against the wall of a house. How high will the ladder be if the bottom of the ladder is 4 feet from the wall? Round your answer to the nearest tenth.
Answers
1. 20 meters
3. 20 meters
5. √315 meters
7. \(\sqrt{445}\) meters
9. \(\sqrt{217}\) meters
11. 10 meters
13. 8 meters
15. \(\sqrt{520}\) meters
17. 18.25 meters
19. 16.9 meters
21. 23.43 feet
23. 6.93 meters
25. 22.20 meters
27. 21.82 meters
29. 40 kilometers
31. 6 ft.

