4.6: Multiply and Divide Mixed Numbers and Complex Fractions (Part 2)
- Page ID
- 6056
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Simplify Expressions with a Fraction Bar
Where does the negative sign go in a fraction? Usually, the negative sign is placed in front of the fraction, but you will sometimes see a fraction with a negative numerator or denominator. Remember that fractions represent division. The fraction \(− \dfrac{1}{3}\) could be the result of dividing \(\dfrac{−1}{3}\), a negative by a positive, or of dividing \(\dfrac{1}{−3}\), a positive by a negative. When the numerator and denominator have different signs, the quotient is negative.
\[\dfrac{-1}{3} = - \dfrac{1}{3} \quad \dfrac{negative}{positive} = negative \quad \dfrac{1}{-3} = - \dfrac{1}{3} \quad \dfrac{positive}{negative} = negative \tag{4.3.46} \nonumber \]
If both the numerator and denominator are negative, then the fraction itself is positive because we are dividing a negative by a negative.
\[\dfrac{-1}{-3} = \dfrac{1}{3} \qquad \dfrac{negative}{negative} = positive \tag{4.3.47} \nonumber \]
For any positive numbers \(a\) and \(b\),
\[\dfrac{-a}{b} = \dfrac{a}{-b} = - \dfrac{a}{b} \]
Which of the following fractions are equivalent to \(\dfrac{7}{−8}\)?
\[\dfrac{-7}{-8}, \dfrac{-7}{8}, \dfrac{7}{8}, - \dfrac{7}{8} \nonumber \]
Solution
The quotient of a positive and a negative is a negative, so \(\dfrac{7}{−8}\) is negative. Of the fractions listed, \(\dfrac{−7}{8}\) and \(− \dfrac{7}{8}\) are also negative.
Which of the following fractions are equivalent to \(\dfrac{-3}{5}\)?
\[\dfrac{-3}{-5}, \dfrac{3}{5}, - \dfrac{3}{5}, \dfrac{3}{-5} \nonumber \]
- Answer
-
\(-\dfrac{3}{5}, \dfrac{3}{-5}\)
Which of the following fractions are equivalent to \(- \dfrac{2}{7}\)?
\[\dfrac{-2}{-7}, \dfrac{-2}{7}, \dfrac{2}{7}, \dfrac{2}{-7} \nonumber \]
- Answer
-
\(\dfrac{-2}{7}, \dfrac{2}{-7}\)
Fraction bars act as grouping symbols. The expressions above and below the fraction bar should be treated as if they were in parentheses. For example, \(\dfrac{4 + 8}{5 − 3}\) means \((4 + 8) ÷ (5 − 3)\). The order of operations tells us to simplify the numerator and the denominator first—as if there were parentheses—before we divide.
We’ll add fraction bars to our set of grouping symbols from Use the Language of Algebra to have a more complete set here.
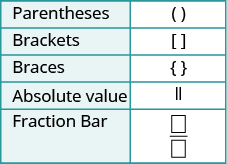
Step 1. Simplify the numerator.
Step 2. Simplify the denominator.
Step 3. Simplify the fraction.
Simplify: \(\dfrac{4 + 8}{5 − 3}\).
Solution
| Simplify the expression in the numerator. | \(\dfrac{12}{5 - 3}\) |
| Simplify the expression in the denominator. | \(\dfrac{12}{2}\) |
| Simplify the fraction. | \(6\) |
Simplify: \(\dfrac{4 + 6}{11 − 2}\).
- Answer
-
\(\dfrac{10}{9}\)
Simplify: \(\dfrac{3 + 5}{18− 2}\).
- Answer
-
\(\dfrac{1}{2}\)
Simplify: \(\dfrac{4 − 2(3)}{2^{2} + 2}\).
Solution
| Use the order of operations. Multiply in the numerator and use the exponent in the denominator. | \(\dfrac{4 - 6}{4 + 2}\) |
| Simplify the numerator and the denominator. | \(\dfrac{-2}{6}\) |
| Simplify the fraction. | \(- \dfrac{1}{3}\) |
Simplify: \(\dfrac{6 − 3(5)}{3^{2} + 3}\).
- Answer
-
\(\dfrac{-3}{4}\)
Simplify: \(\dfrac{4 − 4(6)}{3^{3} + 3}\).
- Answer
-
\(-\dfrac{2}{3}\)
Simplify: \(\dfrac{(8 − 4)^{2}}{8^{2} − 4^{2}}\).
Solution
| Use the order of operations (parentheses first, then exponents). | \(\dfrac{(4)^{2}}{64 - 16}\) |
| Simplify the numerator and denominator. | \(\dfrac{16}{48}\) |
| Simplify the fraction. | \(\dfrac{1}{3}\) |
Simplify: \(\dfrac{(11 − 7)^{2}}{11^{2} − 7^{2}}\).
- Answer
-
\(\dfrac{2}{9}\)
Simplify: \(\dfrac{(6 + 2)^{2}}{6^{2} − 2^{2}}\).
- Answer
-
\(\dfrac{8}{5}\)
Simplify: \(\dfrac{4(−3) + 6(−2)}{−3(2)−2}\).
Solution
| Multiply. | \(\dfrac{-12 + (-12)}{-6 - 2}\) |
| Simplify. | \(\dfrac{-24}{-8} \) |
| Divide. | \(3 \) |
Simplify: \(\dfrac{8(−2) + 4(−3)}{−5(2) + 3}\).
- Answer
-
\(4\)
Simplify: \(\dfrac{7(−1) + 9(−3)}{−5(3) + 2}\).
- Answer
-
\(2\)
Access Additional Online Resources
- Division Involving Mixed Numbers
- Evaluate a Complex Fraction
Key Concepts
- Multiply or divide mixed numbers.
- Convert the mixed numbers to improper fractions.
- Follow the rules for fraction multiplication or division.
- Simplify if possible.
- Simplify a complex fraction.
- Rewrite the complex fraction as a division problem.
- Follow the rules for dividing fractions.
- Simplify if possible.
- Placement of negative sign in a fraction.
- For any positive numbers \(a\) and \(b\), \(\dfrac{-a}{b} = \dfrac{a}{-b} = -\dfrac{a}{b}\).
- Simplify an expression with a fraction bar.
- Simplify the numerator.
- Simplify the denominator.
- Simplify the fraction.
Glossary
- complex fraction
-
A complex fraction is a fraction in which the numerator or the denominator contains a fraction.
Practice Makes Perfect
Multiply and Divide Mixed Numbers
In the following exercises, multiply and write the answer in simplified form.
- \(4 \dfrac{3}{8} \cdot \dfrac{7}{10}\)
- \(2 \dfrac{4}{9} \cdot \dfrac{6}{7}\)
- \(\dfrac{15}{22} \cdot 3 \dfrac{3}{5}\)
- \(\dfrac{25}{36} \cdot 6 \dfrac{3}{10}\)
- \(4 \dfrac{2}{3} (−1 \dfrac{1}{8})\)
- \(2 \dfrac{2}{5} (−2 \dfrac{2}{9})\)
- \(−4 \dfrac{4}{9} \cdot 5 \dfrac{13}{16}\)
- \(−1 \dfrac{7}{20} \cdot 2 \dfrac{11}{12}\)
In the following exercises, divide, and write your answer in simplified form.
- \(5 \dfrac{1}{3}\) ÷ 4
- \(13 \dfrac{1}{2}\) ÷ 9
- −12 ÷ \(3 \dfrac{3}{11}\)
- −7 ÷ \(5 \dfrac{1}{4}\)
- \(6 \dfrac{3}{8} \div 2 \dfrac{1}{8}\)
- \(2 \dfrac{1}{5} \div 1 \dfrac{1}{10}\)
- \(−9 \dfrac{3}{5} \div (−1 \dfrac{3}{5})\)
- \(−18 \dfrac{3}{4} \div (−3 \dfrac{3}{4})\)
Translate Phrases to Expressions with Fractions
In the following exercises, translate each English phrase into an algebraic expression.
- the quotient of 5u and 11
- the quotient of 7v and 13
- the quotient of p and q
- the quotient of a and b
- the quotient of r and the sum of s and 10
- the quotient of A and the difference of 3 and B
Simplify Complex Fractions
In the following exercises, simplify the complex fraction.
- \(\dfrac{\dfrac{2}{3}}{\dfrac{8}{9}}\)
- \(\dfrac{\dfrac{4}{5}}{\dfrac{8}{15}}\)
- \(\dfrac{− \dfrac{8}{21}}{\dfrac{12}{35}}\)
- \(\dfrac{− \dfrac{9}{16}}{\dfrac{33}{40}}\)
- \(\dfrac{− \dfrac{4}{5}}{2}\)
- \(\dfrac{− \dfrac{9}{10}}{3}\)
- \(\dfrac{\dfrac{2}{5}}{8}\)
- \(\dfrac{\dfrac{5}{3}}{10}\)
- \(\dfrac{\dfrac{m}{3}}{\dfrac{n}{2}}\)
- \(\dfrac{\dfrac{r}{5}}{\dfrac{s}{3}}\)
- \(\dfrac{− \dfrac{x}{6}}{− \dfrac{8}{9}}\)
- \(\dfrac{− \dfrac{3}{8}}{− \dfrac{y}{12}}\)
- \(\dfrac{2 \dfrac{4}{5}}{\dfrac{1}{10}}\)
- \(\dfrac{4 \dfrac{2}{3}}{\dfrac{1}{6}}\)
- \(\dfrac{\dfrac{7}{9}}{−2 \dfrac{4}{5}}\)
- \(\dfrac{\dfrac{3}{8}}{−6 \dfrac{3}{4}}\)
Simplify Expressions with a Fraction Bar
In the following exercises, identify the equivalent fractions.
- Which of the following fractions are equivalent to \(\dfrac{5}{−11}\)? $$\dfrac{−5}{−11}, \dfrac{−5}{11}, \dfrac{5}{11}, − \dfrac{5}{11}$$
- Which of the following fractions are equivalent to \(\dfrac{−4}{9}\)? $$\dfrac{−4}{−9}, \dfrac{−4}{9}, \dfrac{4}{9}, − \dfrac{4}{9}$$
- Which of the following fractions are equivalent to \(− \dfrac{11}{3}\)? $$\dfrac{−11}{3}, \dfrac{11}{3}, \dfrac{−11}{−3}, \dfrac{11}{−3}$$
- Which of the following fractions are equivalent to \(− \dfrac{13}{6}\)? $$\dfrac{13}{6}, \dfrac{13}{−6}, \dfrac{−13}{−6}, \dfrac{−13}{6}$$
In the following exercises, simplify.
- \(\dfrac{4 + 11}{8}\)
- \(\dfrac{9 + 3}{7}\)
- \(\dfrac{22 + 3}{10}\)
- \(\dfrac{19 − 4}{6}\)
- \(\dfrac{48}{24 − 15}\)
- \(\dfrac{46}{4 + 4}\)
- \(\dfrac{−6 + 6}{8 + 4}\)
- \(\dfrac{−6 + 3}{17 − 8}\)
- \(\dfrac{22 − 14}{19 − 13}\)
- \(\dfrac{15 + 9}{18 + 12}\)
- \(\dfrac{5 \cdot 8}{−10}\)
- \(\dfrac{3 \cdot 4}{−24}\)
- \(\dfrac{4 \cdot 3}{6 \cdot 6}\)
- \(\dfrac{6 \cdot 6}{9 \cdot 2}\)
- \(\dfrac{4^{2} − 1}{25}\)
- \(\dfrac{7^{2} + 1}{60}\)
- \(\dfrac{8 \cdot 3 + 2 \cdot 9}{14 + 3}\)
- \(\dfrac{9 \cdot 6 − 4 \cdot 7}{22 + 3}\)
- \(\dfrac{15 \cdot 5 − 5^{2}}{2 \cdot 10}\)
- \(\dfrac{12 \cdot 9 − 3^{2}}{3 \cdot 18}\)
- \(\dfrac{5 \cdot 6 − 3 \cdot 4}{4 \cdot 5 − 2 \cdot 3}\)
- \(\dfrac{8 \cdot 9 − 7 \cdot 6}{5 \cdot 6 − 9 \cdot 2}\)
- \(\dfrac{5^{2} − 3^{2}}{3 − 5}\)
- \(\dfrac{6^{2} − 4^{2}}{4 − 6}\)
- \(\dfrac{2 + 4(3)}{−3 − 2^{2}}\)
- \(\dfrac{7 + 3(5)}{−2 − 3^{2}}\)
- \(\dfrac{7 \cdot 4 − 2(8 − 5)}{9 \cdot 3 − 3 \cdot 5}\)
- \(\dfrac{9 \cdot 7 − 3(12 − 8)}{8 \cdot 7 − 6 \cdot 6}\)
- \(\dfrac{9(8 − 2)−3(15 − 7)}{6(7 − 1)−3(17 − 9)}\)
- \(\dfrac{8(9 − 2)−4(14 − 9)}{7(8 − 3)−3(16 − 9)}\)
Everyday Math
- Baking A recipe for chocolate chip cookies calls for \(2 \dfrac{1}{4}\) cups of flour. Graciela wants to double the recipe.
- How much flour will Graciela need? Show your calculation. Write your result as an improper fraction and as a mixed number.
- Measuring cups usually come in sets with cups for \(\dfrac{1}{8}, \dfrac{1}{4}, \dfrac{1}{3}, \dfrac{1}{2}\), and 1 cup. Draw a diagram to show two different ways that Graciela could measure out the flour needed to double the recipe.
- Baking A booth at the county fair sells fudge by the pound. Their award winning “Chocolate Overdose” fudge contains \(2 \dfrac{2}{3}\) cups of chocolate chips per pound.
- How many cups of chocolate chips are in a half-pound of the fudge?
- The owners of the booth make the fudge in 10 -pound batches. How many chocolate chips do they need to make a 10 -pound batch? Write your results as improper fractions and as a mixed numbers.
Writing Exercises
- Explain how to find the reciprocal of a mixed number.
- Explain how to multiply mixed numbers.
- Randy thinks that \(3 \dfrac{1}{2} \cdot 5 \dfrac{1}{4}\) is \(15 \dfrac{1}{8}\). Explain what is wrong with Randy’s thinking.
- Explain why \(− \dfrac{1}{2}, \dfrac{−1}{2}\), and \(\dfrac{1}{−2}\) are equivalent.
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
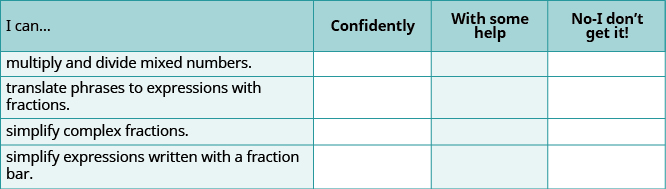
(b) What does this checklist tell you about your mastery of this section? What steps will you take to improve?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


