7.4: Distributive Property
- Page ID
- 5035
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Simplify expressions using the distributive property
- Evaluate expressions using the distributive property
Before you get started, take this readiness quiz.
- Multiply: 3(0.25). If you missed this problem, review Example 5.3.5
- Simplify: 10 − (−2)(3). If you missed this problem, review Example 3.7.5.
- Combine like terms: 9y + 17 + 3y − 2. If you missed this problem, review Example 2.3.10.
Simplify Expressions Using the Distributive Property
Suppose three friends are going to the movies. They each need $9.25; that is, 9 dollars and 1 quarter. How much money do they need all together? You can think about the dollars separately from the quarters.


They need 3 times $9, so $27, and 3 times 1 quarter, so 75 cents. In total, they need $27.75. If you think about doing the math in this way, you are using the Distributive Property.
If a, b, c are real numbers, then a(b + c) = ab + ac.
Back to our friends at the movies, we could show the math steps we take to find the total amount of money they need like this:
\[\begin{split} 3(9&.25) \\ 3(9 &+ 0.25) \\ 3(9) &+ 3(0.25) \\ 27 &+ 0.75 \\ 27&.75 \end{split}\]
In algebra, we use the Distributive Property to remove parentheses as we simplify expressions. For example, if we are asked to simplify the expression 3(x + 4), the order of operations says to work in the parentheses first. But we cannot add x and 4, since they are not like terms. So we use the Distributive Property, as shown in Example \(\PageIndex{1}\).
Simplify: 3(x + 4).
Solution
| Distribute. | 3 • x + 3 • 4 |
| Multiply. | 3x + 12 |
Simplify: 4(x + 2).
- Answer
-
\(4x+8\)
Simplify: 6(x + 7).
- Answer
-
6x + 42
Some students find it helpful to draw in arrows to remind them how to use the Distributive Property. Then the first step in Example 7.17 would look like this:
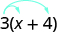
\[3 \cdot x + 3 \cdot 4\]
Simplify: 6(5y + 1).
Solution
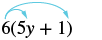
| Distribute. | $$6 \cdot 5y + 6 \cdot 1$$ |
| Multiply. | $$30y + 6$$ |
Simplify: 9(3y + 8).
- Answer
-
27y + 72
Simplify: 5(5w + 9).
- Answer
-
25w + 45
The distributive property can be used to simplify expressions that look slightly different from a(b + c). Here are two other forms.
If a, b, c are real numbers, then\[a(b + c) = ab + ac$$Other forms$$a(b − c) = ab − ac$$$$(b + c)a = ba + ca\]
Simplify: 2(x − 3).
Solution
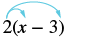
| Distribute. | $$2 \cdot x + 2 \cdot 3$$ |
| Multiply. | $$2x - 6$$ |
Simplify: 7(x − 6).
- Answer
-
7x - 42
Simplify: 8(x − 5).
- Answer
-
8x - 40
Do you remember how to multiply a fraction by a whole number? We’ll need to do that in the next two examples.
Simplify: \(\dfrac{3}{4}\)(n + 12).
Solution
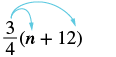
| Distribute. | $$\dfrac{3}{4} \cdot n + \dfrac{3}{4} \cdot 12$$ |
| Multiply. | $$\dfrac{3}{4}n + 9$$ |
Simplify: \(\dfrac{2}{5}\)(p + 10).
- Answer
-
\(\frac{2}{5}p + 4 \)
Simplify: \(\dfrac{3}{7}\)(u + 21).
- Answer
-
\(\frac{3}{7}u +9 \)
Simplify: \(8 \left(\dfrac{3}{8}x + \dfrac{1}{4}\right)\).
Solution
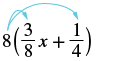
| Distribute. | $$8 \cdot \dfrac{3}{8}x + 8 \cdot \dfrac{1}{4}$$ |
| Multiply. | $$3x + 2$$ |
Simplify: \(6 \left(\dfrac{5}{6}y + \dfrac{1}{2}\right)\).
- Answer
-
5y + 3
Simplify: \(12 \left(\dfrac{1}{3}n + \dfrac{3}{4}\right)\).
- Answer
-
4n + 9
Using the Distributive Property as shown in the next example will be very useful when we solve money applications later.
Simplify: 100(0.3 + 0.25q).
Solution
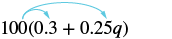
| Distribute. | $$100(0.3) + 100(0.25q)$$ |
| Multiply. | $$30 + 25q$$ |
Simplify: 100(0.7 + 0.15p).
- Answer
-
70 + 15p
Simplify: 100(0.04 + 0.35d).
- Answer
-
4 + 35d
In the next example we’ll multiply by a variable. We’ll need to do this in a later chapter.
Simplify: \(m(n − 4)\).
Solution
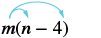
| Distribute. | $$m \cdot n - m \cdot 4$$ |
| Multiply. | $$mn - 4m$$ |
Notice that we wrote m • 4 as 4m. We can do this because of the Commutative Property of Multiplication. When a term is the product of a number and a variable, we write the number first.
Simplify: r(s − 2).
- Answer
-
rs - 2r
Simplify: y(z − 8).
- Answer
-
yz - 8y
The next example will use the ‘backwards’ form of the Distributive Property, (b + c)a = ba + ca.
Simplify: (x + 8)p.
Solution
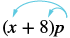
| Distribute. | $$px + 8p$$ |
Simplify: (x + 2)p.
- Answer
-
xp + 2p
Simplify: (y + 4)q.
- Answer
-
yq + 4q
When you distribute a negative number, you need to be extra careful to get the signs correct.
Simplify: −2(4y + 1).
Solution
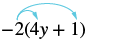
| Distribute. | $$-2 \cdot 4y + (-2) \cdot 1$$ |
| Simplify. | $$-8y - 2$$ |
Simplify: −3(6m + 5).
- Answer
-
-18m - 15
Simplify: −6(8n + 11).
- Answer
-
-48n - 66
Simplify: −11(4 − 3a).
Solution
| Distribute. | $$-11 \cdot 4 - (-11) \cdot 3a$$ |
| Multiply. | $$-44 - (-33a)$$ |
| Simplify. | $$-44 + 33a$$ |
You could also write the result as 33a − 44. Do you know why?
Simplify: −5(2 − 3a).
- Answer
-
-10 + 15a
Simplify: −7(8 − 15y).
- Answer
-
-56 + 105y
In the next example, we will show how to use the Distributive Property to find the opposite of an expression. Remember, −a = −1 • a.
Simplify: −(y + 5).
Solution
| Multiplying by −1 results in the opposite. | $$-1 (y + 5)$$ |
| Distribute. | $$-1 \cdot y + (-1) \cdot 5$$ |
| Simplify. | $$-y + (-5)$$ |
| Simplify. | $$-y -5$$ |
Simplify: −(z − 11).
- Answer
-
-z + 11
Simplify: −(x − 4).
- Answer
-
-x + 4
Sometimes we need to use the Distributive Property as part of the order of operations. Start by looking at the parentheses. If the expression inside the parentheses cannot be simplified, the next step would be multiply using the distributive property, which removes the parentheses. The next two examples will illustrate this.
Simplify: 8 − 2(x + 3).
Solution
| Distribute. | $$8 - 2 \cdot x - 2 \cdot 3$$ |
| Multiply. | $$8 - 2x - 6$$ |
| Combine like terms. | $$-2x + 2$$ |
Simplify: 9 − 3(x + 2).
- Answer
-
-3x + 3
Simplify: 7x − 5(x + 4).
- Answer
-
2x - 20
Simplify: 4(x − 8) − (x + 3).
Solution
| Distribute. | $$4x - 32 - x - 3$$ |
| Combine like terms. | $$3x - 35$$ |
Simplify: 6(x − 9) − (x + 12).
- Answer
-
5x - 66
Simplify: 8(x − 1) − (x + 5).
- Answer
-
7x - 13
Evaluate Expressions Using the Distributive Property
Some students need to be convinced that the Distributive Property always works. In the examples below, we will practice evaluating some of the expressions from previous examples; in part (a), we will evaluate the form with parentheses, and in part (b) we will evaluate the form we got after distributing. If we evaluate both expressions correctly, this will show that they are indeed equal.
When y = 10 evaluate: (a) 6(5y + 1) (b) 6 • 5y + 6 • 1.
Solution
(a) 6(5y + 1)
| Substitute \(\textcolor{red}{10}\) for y. | $$6(5 \cdot \textcolor{red}{10} + 1)$$ |
| Simplify in the parentheses. | $$6(51)$$ |
| Multiply. | $$306$$ |
(b) 6 • 5y + 6 • 1
| Substitute \(\textcolor{red}{10}\) for y. | $$6 \cdot 5 \cdot \textcolor{red}{10} + 6 \cdot 1$$ |
| Simplify. | $$300 + 6$$ |
| Add. | $$306$$ |
Notice, the answers are the same. When y = 10, 6(5y + 1) = 6 • 5y + 6 • 1. Try it yourself for a different value of y.
Evaluate when w = 3: (a) 5(5w + 9) (b) 5 • 5w + 5 • 9.
- Answer a
-
\(120\)
- Answer b
-
\(120\)
Evaluate when y = 2: (a) 9(3y + 8) (b) 9 • 3y + 9 • 8.
- Answer a
-
\(126\)
- Answer b
-
\(126\)
When y = 3, evaluate (a) −2(4y + 1) (b) −2 • 4y + (−2) • 1.
Solution
(a) −2(4y + 1)
| Substitute \(\textcolor{red}{3}\) for y. | $$-2(4 \cdot \textcolor{red}{3} + 1)$$ |
| Simplify in the parentheses. | $$-2(13)$$ |
| Multiply. | $$-26$$ |
(b) −2 • 4y + (−2) • 1
| Substitute \(\textcolor{red}{3}\) for y. | $$-2 \cdot 4 \cdot \textcolor{red}{3} + (-2) \cdot 1$$ |
| Multiply. | $$-24 - 2$$ |
| Subtract. | $$-26$$ |
| The answers are the same when y = 3. | $$-2(4y + 1) = -8y - 2$$ |
Evaluate when n = −2: (a) −6(8n + 11) (b) −6 • 8n + (−6) • 11.
- Answer a
-
\(30\)
- Answer b
-
\(30\)
Evaluate when m = −1: (a) −3(6m + 5) (b) −3 • 6m + (−3) • 5.
- Answer a
-
\(3\)
- Answer b
-
\(3\)
When y = 35 evaluate (a) −(y + 5) and (b) −y − 5 to show that −(y + 5) = −y − 5.
Solution
(a) −(y + 5)
| Substitute \(\textcolor{red}{35}\) for y. | $$-(\textcolor{red}{35} + 5)$$ |
| Add in the parentheses. | $$-(40)$$ |
| Simplify. | $$-40$$ |
(b) −y − 5
| Substitute \(\textcolor{red}{35}\) for y. | $$-\textcolor{red}{35} - 5$$ |
| Simplify. | $$-40$$ |
| The answers are the same when y = 35, demonstrating that | $$-(y + 5) = -y - 5$$ |
Evaluate when x = 36: (a) −(x − 4) (b) −x + 4 to show that −(x − 4) = − x + 4.
- Answer a
-
\(-32\)
- Answer b
-
\(-32\)
Evaluate when z = 55: (a) −(z − 10) (b) −z + 10 to show that −(z − 10) = − z + 10.
- Answer a
-
\(-45\)
- Answer b
-
\(-45\)
Model Distribution
The Distributive Property
Practice Makes Perfect
Simplify Expressions Using the Distributive Property
In the following exercises, simplify using the distributive property.
- 4(x + 8)
- 3(a + 9)
- 8(4y + 9)
- 9(3w + 7)
- 6(c − 13)
- 7(y − 13)
- 7(3p − 8)
- 5(7u − 4)
- \(\dfrac{1}{2}\)(n + 8)
- \(\dfrac{1}{3}\)(u + 9)
- \(\dfrac{1}{4}\)(3q + 12)
- \(\dfrac{1}{5}\)(4m + 20)
- \(9 \left(\dfrac{5}{9} y − \dfrac{1}{3}\right)\)
- \(10 \left(\dfrac{3}{10} x − \dfrac{2}{5}\right)\)
- \(12 \left(\dfrac{1}{4} + \dfrac{2}{3} r\right)\)
- \(12 \left(\dfrac{1}{6} + \dfrac{3}{4} s\right)\)
- r(s − 18)
- u(v − 10)
- (y + 4)p
- (a + 7)x
- −2(y + 13)
- −3(a + 11)
- −7(4p + 1)
- −9(9a + 4)
- −3(x − 6)
- −4(q − 7)
- −9(3a − 7)
- −6(7x − 8)
- −(r + 7)
- −(q + 11)
- −(3x − 7)
- −(5p − 4)
- 5 + 9(n − 6)
- 12 + 8(u − 1)
- 16 − 3(y + 8)
- 18 − 4(x + 2)
- 4 − 11(3c − 2)
- 9 − 6(7n − 5)
- 22 − (a + 3)
- 8 − (r − 7)
- −12 − (u + 10)
- −4 − (c − 10)
- (5m − 3) − (m + 7)
- (4y − 1) − (y − 2)
- 5(2n + 9) + 12(n − 3)
- 9(5u + 8) + 2(u − 6)
- 9(8x − 3) − (−2)
- 4(6x − 1) − (−8)
- 14(c − 1) − 8(c − 6)
- 11(n − 7) − 5(n − 1)
- 6(7y + 8) − (30y − 15)
- 7(3n + 9) − (4n − 13)
Evaluate Expressions Using the Distributive Property
In the following exercises, evaluate both expressions for the given value.
- If v = −2, evaluate
- 6(4v + 7)
- 6 · 4v + 6 · 7
- If u = −1, evaluate
- 8(5u + 12)
- 8 · 5u + 8 · 12
- If n = \(\dfrac{2}{3}\), evaluate
- \(3 \left(n + \dfrac{5}{6}\right)\)
- 3 • n + 3 • \(\dfrac{5}{6}\)
- If y = 3 4 , evaluate
- 4 ⎛ ⎝ y + 3 8 ⎞ ⎠
- 4 • y + 4 • \(\dfrac{3}{8}\)
- If y = \(\dfrac{7}{12}\), evaluate
- −3(4y + 15)
- 3 • 4y + (−3) • 15
- If p = \(\dfrac{23}{30}\), evaluate
- −6(5p + 11)
- −6 • 5p + (−6) • 11
- If m = 0.4, evaluate
- −10(3m − 0.9)
- −10 • 3m − (−10)(0.9)
- If n = 0.75, evaluate
- −100(5n + 1.5)
- −100 • 5n + (−100)(1.5)
- If y = −25, evaluate
- −(y − 25)
- −y + 25
- If w = −80, evaluate
- −(w − 80)
- −w + 80
- If p = 0.19, evaluate
- −(p + 0.72)
- −p − 0.72
- If q = 0.55, evaluate
- −(q + 0.48)
- −q − 0.48
Everyday Math
- Buying by the case Joe can buy his favorite ice tea at a convenience store for $1.99 per bottle. At the grocery store, he can buy a case of 12 bottles for $23.88.
- Use the distributive property to find the cost of 12 bottles bought individually at the convenience store. (Hint: notice that $1.99 is $2 − $0.01.)
- Is it a bargain to buy the iced tea at the grocery store by the case?
- Multi-pack purchase Adele’s shampoo sells for $3.97 per bottle at the drug store. At the warehouse store, the same shampoo is sold as a 3-pack for $10.49.
- Show how you can use the distributive property to find the cost of 3 bottles bought individually at the drug store.
- How much would Adele save by buying the 3-pack at the warehouse store?
Writing Exercises
- Simplify \(8 \left(x − \dfrac{1}{4}\right)\) using the distributive property and explain each step.
- Explain how you can multiply 4($5.97) without paper or a calculator by thinking of $5.97 as 6 − 0.03 and then using the distributive property.
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
(b) What does this checklist tell you about your mastery of this section? What steps will you take to improve?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


