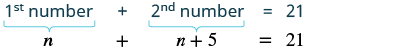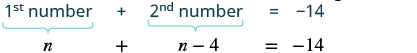9.2: Use a Problem Solving Strategy (Part 2)
- Page ID
- 7020
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Some number word problems ask you to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. We will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
One number is five more than another. The sum of the numbers is twenty-one. Find the numbers.
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | You are looking for two numbers. |
| Step 3. Name. Choose a variable to represent the first number. What do you know about the second number? Translate. |
Let n = 1st number. One number is five more than another. x + 5 = 2nd number |
| Step 4. Translate. Restate the problem as one sentence with all the important information. Translate into an equation. Substitute the variable expressions. |
The sum of the numbers is 21. The sum of the 1st number and the 2nd number is 21.
|
| Step 5. Solve the equation. | $$n + n + 5 = 21 \tag{9.1.15}$$ |
| Combine like terms. | $$2n + 5 = 21 \tag{9.1.16}$$ |
| Subtract five from both sides and simplify. | $$2n = 16 \tag{9.1.17}$$ |
| Divide by two and simplify. | $$n = 8 \qquad 1^{st}\; number \tag{9.1.18}$$ |
| Find the second number too. | $$n + 5 \qquad 2^{nd}\; number \tag{9.1.19}$$ |
| Substitute n = 8. | $$\textcolor{red}{8} + 5 \tag{9.1.20}$$ |
| Step 6. Check: Do these numbers check in the problem? Is one number 5 more than the other? Is thirteen, 5 more than 8? Yes. | $$\begin{split} 13 &\stackrel{?}{=} 8 + 5 \\ 13 &= 13\; \checkmark \end{split}$$ |
| Is the sum of the two numbers 21? | $$\begin{split} 8 + 13 &= 21 \\ 21 &= 21\; \checkmark \end{split}$$ |
| Step 7. Answer the question. | The numbers are 8 and 13. |
One number is six more than another. The sum of the numbers is twenty-four. Find the numbers.
- Answer
-
9, 15
The sum of two numbers is fifty-eight. One number is four more than the other. Find the numbers.
- Answer
-
27, 31
The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | two numbers |
| Step 3. Name. Choose a variable. What do you know about the second number? Translate. |
Let n = 1st number One number is 4 less than the other. n - 4 = 2nd number |
| Step 4. Translate. Write as one sentence. Translate into an equation. Substitute the variable expressions. |
The sum of two numbers is negative fourteen.
|
| Step 5. Solve the equation. | $$n + n - 4 = -14 \tag{9.1.21}$$ |
| Combine like terms. | $$2n - 4 = -14 \tag{9.1.22}$$ |
| Add 4 to each side and simplify. | $$2n = -10 \tag{9.1.23}$$ |
| Divide by 2. | $$n = -5 \qquad 1^{st}\; number \tag{9.1.24}$$ |
| Substitute n = −5 to find the 2nd number. | $$\begin{split} n - &4 \qquad 2^{nd}\; number \\ \textcolor{red}{-5} - &4 \\ - &9 \end{split}$$ |
| Step 6. Check: Is −9 four less than −5? | $$\begin{split} -5 - 4 &\stackrel{?}{=} -9\\ -9&= -9\; \checkmark \end{split}$$ |
| Is their sum −14? | $$\begin{split} -5 + (-9) &\stackrel{?}{=} -14 \\ -14 &= -14\; \checkmark \end{split}$$ |
| Step 7. Answer the question. | The numbers are −5 and −9. |
The sum of two numbers is negative twenty-three. One number is 7 less than the other. Find the numbers.
- Answer
-
-8, -15
The sum of two numbers is negative eighteen. One number is 40 more than the other. Find the numbers.
- Answer
-
-29, 11
One number is ten more than twice another. Their sum is one. Find the numbers.
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | two numbers |
| Step 3. Name. Choose a variable. One number is ten more than twice another. |
Let x = 1st number 2x + 10 = 2nd number |
| Step 4. Translate. Restate as one sentence. | Their sum is one. |
| Translate into an equation. |  |
| Step 5. Solve the equation. | $$x + 2x + 10 = 1 \tag{9.1.25}$$ |
| Combine like terms. | $$3x + 10 = 1 \tag{9.1.26}$$ |
| Subtract 10 from each side. | $$3x = -9 \tag{9.1.27}$$ |
| Divide each side by 3 to get the first number. | $$x = -3 \tag{9.1.28}$$ |
| Substitute to get the second number. | $$\begin{split} 2x + &10 \\ 2(\textcolor{red}{-3}) + &10 \\ &4 \end{split}$$ |
| Step 6. Check: Is 4 ten more than twice −3? | $$\begin{split} 2(-3) + 10 &\stackrel{?}{=} 4 \\ -6 + 10 &= 4 \\ 4 &= 4\; \checkmark \end{split}$$ |
| Is their sum 1? | $$\begin{split} -3 + 4 &\stackrel{?}{=} 1 \\ 1 &= 1\; \checkmark \end{split}$$ |
| Step 7. Answer the question. | The numbers are −3 and 4. |
One number is eight more than twice another. Their sum is negative four. Find the numbers.
- Answer
-
-4, 0
One number is three more than three times another. Their sum is negative five. Find the numbers.
- Answer
-
-2, -3
Consecutive integers are integers that immediately follow each other. Some examples of consecutive integers are:
\[\ldots 1, 2, 3, 4, \ldots \tag{9.1.29}\]
\[\ldots -10, -9, -8, -7, \ldots \tag{9.1.30}\]
\[\ldots 150, 151, 152, 153, \ldots \tag{9.1.31}\]
Notice that each number is one more than the number preceding it. So if we define the first integer as n, the next consecutive integer is n + 1. The one after that is one more than n + 1, so it is n + 1 + 1, or n + 2.
\[\begin{split} n \qquad &1^{st}\; integer \\ n + 1 \qquad &2^{nd}\; consecutive\; integer \\ n + 2 \qquad &3^{rd}\; consecutive\; integer \end{split}\]
The sum of two consecutive integers is 47. Find the numbers.
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | two consecutive integers |
| Step 3. Name. |
Let n = 1st integer n + 1 = next consecutive integer |
| Step 4. Translate. Restate as one sentence. Translate into an equation. | 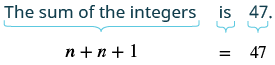 |
| Step 5. Solve the equation. | $$n + n + 1 = 47 \tag{9.1.32}$$ |
| Combine like terms. | $$2n + 1 = 47 \tag{9.1.33}$$ |
| Subtract 1 from each side. | $$2n = 46 \tag{9.1.34}$$ |
| Divide each side by 2. | $$n = 23 \qquad 1^{st}\; integer \tag{9.1.35}$$ |
| Substitute to get the second number. | $$\begin{split} n + 1& \qquad 2^{nd}\; integer \\ \textcolor{red}{23} + 1& \\ 24& \end{split}$$ |
| Step 6. Check. | $$\begin{split} 23 + 24 &\stackrel{?}{=} 47 \\ 47 &= 47\; \checkmark \end{split}$$ |
| Step 7. Answer the question. | The two consecutive integers are 23 and 24. |
The sum of two consecutive integers is 95. Find the numbers.
- Answer
-
47, 48
The sum of two consecutive integers is −31. Find the numbers.
- Answer
-
-15, -16
Find three consecutive integers whose sum is 42.
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | three consecutive integers |
| Step 3. Name. |
Let n = 1st integer n + 1 = 2nd consecutive integer n + 2 = 3rd consecutive integer |
| Step 4. Translate. Restate as one sentence. Translate into an equation. | 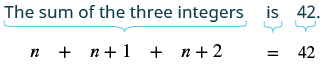 |
| Step 5. Solve the equation. | $$n + n + 1 + n + 2 = 42 \tag{9.1.36}$$ |
| Combine like terms. | $$3n + 3 = 42 \tag{9.1.37}$$ |
| Subtract 3 from each side. | $$3n = 39 \tag{9.1.38}$$ |
| Divide each side by 3. | $$n = 13 \qquad 1^{st}\; integer \tag{9.1.39}$$ |
| Substitute to get the second number. | $$\begin{split} n + 1& \qquad 2^{nd}\; integer \\ \textcolor{red}{13} + 1& \\ 24& \end{split}$$ |
| Substitute to get the third number. | $$\begin{split} n + 2& \qquad 3^{rd}\; integer \\ \textcolor{red}{13} + 2& \\ 15& \end{split}$$ |
| Step 6. Check. | $$\begin{split} 13 + 14 + 15 &\stackrel{?}{=} 42 \\ 42 &= 42\; \checkmark \end{split}$$ |
| Step 7. Answer the question. | The three consecutive integers are 13, 14, and 15. |
Find three consecutive integers whose sum is 96.
- Answer
-
31, 32, 33
Find three consecutive integers whose sum is −36.
- Answer
-
-11, -12, -13
Practice Makes Perfect
Use a Problem-solving Strategy for Word Problems
In the following exercises, use the problem-solving strategy for word problems to solve. Answer in complete sentences.
- Two-thirds of the children in the fourth-grade class are girls. If there are 20 girls, what is the total number of children in the class?
- Three-fifths of the members of the school choir are women. If there are 24 women, what is the total number of choir members?
- Zachary has 25 country music CDs, which is one-fifth of his CD collection. How many CDs does Zachary have?
- One-fourth of the candies in a bag of are red. If there are 23 red candies, how many candies are in the bag?
- There are 16 girls in a school club. The number of girls is 4 more than twice the number of boys. Find the number of boys in the club.
- There are 18 Cub Scouts in Troop 645. The number of scouts is 3 more than five times the number of adult leaders. Find the number of adult leaders.
- Lee is emptying dishes and glasses from the dishwasher. The number of dishes is 8 less than the number of glasses. If there are 9 dishes, what is the number of glasses?
- The number of puppies in the pet store window is twelve less than the number of dogs in the store. If there are 6 puppies in the window, what is the number of dogs in the store?
- After 3 months on a diet, Lisa had lost 12% of her original weight. She lost 21 pounds. What was Lisa's original weight?
- Tricia got a 6% raise on her weekly salary. The raise was $30 per week. What was her original weekly salary?
- Tim left a $9 tip for a $50 restaurant bill. What percent tip did he leave?
- Rashid left a $15 tip for a $75 restaurant bill. What percent tip did he leave?
- Yuki bought a dress on sale for $72. The sale price was 60% of the original price. What was the original price of the dress?
- Kim bought a pair of shoes on sale for $40.50. The sale price was 45% of the original price. What was the original price of the shoes?
Solve Number Problems
In the following exercises, solve each number word problem.
- The sum of a number and eight is 12. Find the number.
- The sum of a number and nine is 17. Find the number.
- The difference of a number and twelve is 3. Find the number.
- The difference of a number and eight is 4. Find the number.
- The sum of three times a number and eight is 23. Find the number.
- The sum of twice a number and six is 14. Find the number.
- The difference of twice a number and seven is 17. Find the number.
- The difference of four times a number and seven is 21. Find the number.
- Three times the sum of a number and nine is 12. Find the number.
- Six times the sum of a number and eight is 30. Find the number.
- One number is six more than the other. Their sum is forty-two. Find the numbers.
- One number is five more than the other. Their sum is thirty-three. Find the numbers.
- The sum of two numbers is twenty. One number is four less than the other. Find the numbers.
- The sum of two numbers is twenty-seven. One number is seven less than the other. Find the numbers.
- A number is one more than twice another number. Their sum is negative five. Find the numbers.
- One number is six more than five times another. Their sum is six. Find the numbers.
- The sum of two numbers is fourteen. One number is two less than three times the other. Find the numbers.
- The sum of two numbers is zero. One number is nine less than twice the other. Find the numbers.
- One number is fourteen less than another. If their sum is increased by seven, the result is 85. Find the numbers.
- One number is eleven less than another. If their sum is increased by eight, the result is 71. Find the numbers.
- The sum of two consecutive integers is 77. Find the integers.
- The sum of two consecutive integers is 89. Find the integers.
- The sum of two consecutive integers is −23. Find the integers.
- The sum of two consecutive integers is −37. Find the integers.
- The sum of three consecutive integers is 78. Find the integers.
- The sum of three consecutive integers is 60. Find the integers.
- Find three consecutive integers whose sum is −36.
- Find three consecutive integers whose sum is −3.
Everyday Math
- Shopping Patty paid $35 for a purse on sale for $10 off the original price. What was the original price of the purse?
- Shopping Travis bought a pair of boots on sale for $25 off the original price. He paid $60 for the boots. What was the original price of the boots?
- Shopping Minh spent $6.25 on 5 sticker books to give his nephews. Find the cost of each sticker book.
- Shopping Alicia bought a package of 8 peaches for $3.20. Find the cost of each peach.
- Shopping Tom paid $1,166.40 for a new refrigerator, including $86.40 tax. What was the price of the refrigerator before tax?
- Shopping Kenji paid $2,279 for a new living room set, including $129 tax. What was the price of the living room set before tax?
Writing Exercises
- Write a few sentences about your thoughts and opinions of word problems. Are these thoughts positive, negative, or neutral? If they are negative, how might you change your way of thinking in order to do better?
- When you start to solve a word problem, how do you decide what to let the variable represent?
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
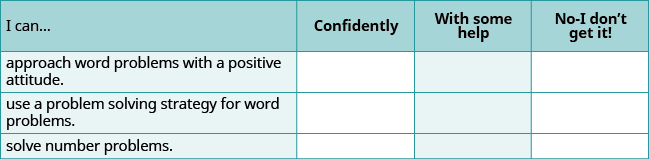
(b) If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math, every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."