3.E: Polynomial and Rational Functions(Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
3.1 Complex Numbers
Verbal
1) Explain how to add complex numbers.
- Answer
-
Add the real parts together and the imaginary parts together.
2) What is the basic principle in multiplication of complex numbers?
3) Give an example to show the product of two imaginary numbers is not always imaginary.
- Answer
-
i times i equals −1, which is not imaginary (answers vary)
4) What is a characteristic of the plot of a real number in the complex plane?
Algebraic
For the exercises 5-10, evaluate the algebraic expressions.
5) If f(x)=x2+x−4, evaluate f(2i).
- Answer
-
−8+2i
6) If f(x)=x3−2, evaluate f(i).
7) If f(x)=x2+3x+5,evaluate f(2+i).
- Answer
-
14+7i
8) If f(x)=2x2+x−3, evaluate f(2−3i).
9) If f(x)=x+12−x, evaluate f(5i).
- Answer
-
−2329+1529i
10) If f(x)=1+2xx+3, evaluate f(4i).
Graphical
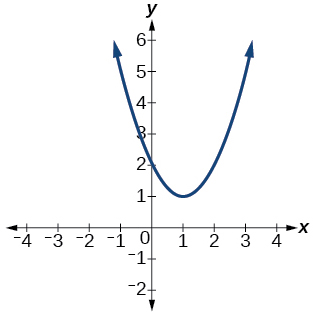
For the exercises 11-12, determine the number of real and nonreal solutions for each quadratic function shown.
11)
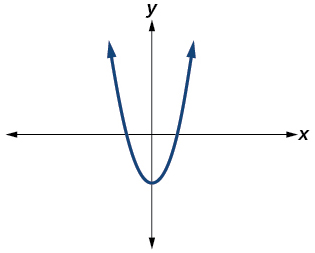
- Answer
-
2 real and 0 nonreal
12)
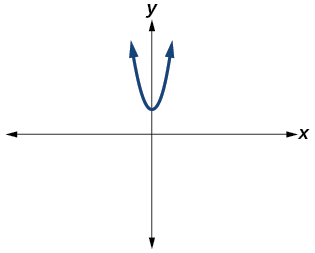
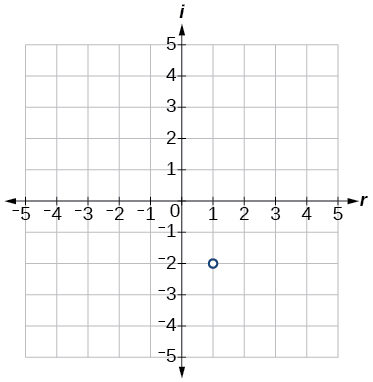
For the exercises 13-16, plot the complex numbers on the complex plane.
13) 1−2i
- Answer
-
14) −2+3i
15) i
- Answer
-
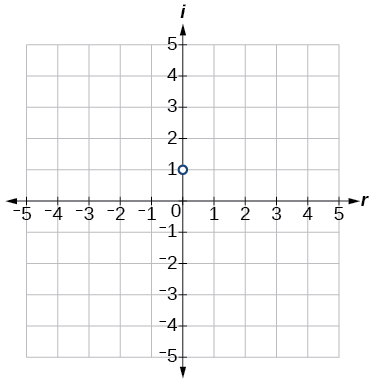
16) −3−4i
Numeric
For the exercises 17-43, perform the indicated operation and express the result as a simplified complex number.
17) (3+2i)+(5−3i)
- Answer
-
8−i
18) (−2−4i)+(1+6i)
19) (−5+3i)−(6−i)
- Answer
-
−11+4i
20) (2−3i)−(3+2i)
21) (−4+4i)−(−6+9i)
- Answer
-
2−5i
22) (2+3i)(4i)
23) (5−2i)(3i)
- Answer
-
6+15i
24) (6−2i)(5)
25) (−2+4i)(8)
- Answer
-
−16+32i
26) (2+3i)(4−i)
27) (−1+2i)(−2+3i)
- Answer
-
−4−7i
28) (4−2i)(4+2i)
29) (3+4i)(3−4i)
- Answer
-
25
30) 3+4i2
31) 6−2i3
- Answer
-
2−23i
32) −5+3i2i
33) 6+4ii
- Answer
-
4−6i
34) 2−3i4+3i
35) 3+4i2−i
- Answer
-
25+115i
36) 2+3i2−3i
37) √−9+3√−16
- Answer
-
15i
38) −√−4−4√−25
39) 2+√−122
- Answer
-
1+i√3
40) 4+√−202
41) i8
- Answer
-
1
42) i15
43) i22
- Answer
-
−1
Technology
For the exercises 44-48, use a calculator to help answer the questions.
44) Evaluate (1+i)k for k=4,8, and 12.Predict the value if k=16.
45) Evaluate (1−i)k for k=2,6, and 10.Predict the value if k=14.
- Answer
-
128i
46) Evaluate (1+i)k−(1−i)k for k=4, 8, and 12. Predict the value for k=16.
47) Show that a solution of x6+1=0 is √32+12i.
- Answer
-
(√32+12i)6=−1
48) Show that a solution of x8−1=0 is √22+√22i.
Extensions
For the exercises 49-58, evaluate the expressions, writing the result as a simplified complex number.
49) 1i+4i3
- Answer
-
3i
50) 1i11−1i21
51) i7(1+i2)
- Answer
-
0
52) i−3+5i7
53) (2+i)(4−2i)(1+i)
- Answer
-
5–5i
54) (1+3i)(2−4i)(1+2i)
55) (3+i)2(1+2i)2
- Answer
-
−2i
56) 3+2i2+i+(4+3i)
57) 4+ii+3−4i1−i
- Answer
-
92−92i
58) 3+2i1+2i−2−3i3+i
3.2 Quadratic Functions
Verbal
1) Explain the advantage of writing a quadratic function in standard form.
- Answer
-
When written in that form, the vertex can be easily identified.
2) How can the vertex of a parabola be used in solving real world problems?
3) Explain why the condition of a≠0 is imposed in the definition of the quadratic function.
- Answer
-
If a=0 then the function becomes a linear function.
4) What is another name for the standard form of a quadratic function?
5) What two algebraic methods can be used to find the horizontal intercepts of a quadratic function?
- Answer
-
If possible, we can use factoring. Otherwise, we can use the quadratic formula.
Algebraic
For the exercises 6-13, rewrite the quadratic functions in standard form and give the vertex.
6) f(x)=x2−12x+32
7) g(x)=x2+2x−3
- Answer
-
g(x)=(x+1)2−4, Vertex (−1,−4)
8) f(x)=x2−x
9) f(x)=x2+5x−2
- Answer
-
f(x)=(x+52)2−334, Vertex (−52,−334)
10) h(x)=2x2+8x−10
11) k(x)=3x2−6x−9
- Answer
-
k(x)=3(x−1)2−12, Vertex (1,−12)
12) f(x)=2x2−6x
13) f(x)=3x2−5x−1
- Answer
-
f(x)=3(x−56)2−3712, Vertex (56,−3712)
For the exercises 14-20, determine whether there is a minimum or maximum value to each quadratic function. Find the value and the axis of symmetry.
14) y(x)=2x2+10x+12
15) f(x)=2x2−10x+4
- Answer
-
Minimum is −172 and occurs at 52. Axis of symmetry is x=52.
16) f(x)=−x2+4x+3
17) f(x)=4x2+x−1
- Answer
-
Minimum is −1716 and occurs at −18. Axis of symmetry is x=−18.
18) h(t)=−4t2+6t−1
19) f(x)=12x2+3x+1
- Answer
-
Minimum is −72 and occurs at −3. Axis of symmetry is x=−3.
20) f(x)=−13x2−2x+3
For the exercises 21-25, determine the domain and range of the quadratic function.
21) f(x)=(x−3)2+2
- Answer
-
Domain is (−∞,∞). Range is [2,∞).
22) f(x)=−2(x+3)2−6
23) f(x)=x2+6x+4
- Answer
-
Domain is (−∞,∞). Range is [−5,∞).
24) f(x)=2x2−4x+2
25) k(x)=3x2−6x−9
- Answer
-
Domain is (−∞,∞). Range is [−12,∞).
For the exercises 26-44, solve the equations over the complex numbers.
26) x2=−25
27) x2=−8
- Answer
-
2i√2,−2i√2
28) x2+36=0
29) x2+27=0
- Answer
-
3i√3,−3i√3
30) x2+2x+5=0
31) x2−4x+5=0
- Answer
-
2+i,2−i
32) x2+8x+25=0
33) x2−4x+13=0
- Answer
-
2+3i,2−3i
34) x2+6x+25=0
35) x2−10x+26=0
- Answer
-
5+i,5−i
36) x2−6x+10=0
37) x(x−4)=20
- Answer
-
2+2√6,2−2√6
38) x(x−2)=10
39) 2x2+2x+5=0
- Answer
-
{−12+32i,−12−32i}
40) 5x2−8x+5=0
41) 5x2+6x+2=0
- Answer
-
{−35+15i,−35−15i}
42) 2x2−6x+5=0
43) x2+x+2=0
- Answer
-
{−12+12i√7,−12−12i√7}
44) x2−2x+4=0
For the exercises 45-52, use the vertex (h,k) and a point on the graph (x,y) to find the general form of the equation of the quadratic function.
45) (h,k)=(2,0),(x,y)=(4,4)
- Answer
-
f(x)=x2−4x+4
46) (h,k)=(−2,−1),(x,y)=(−4,3)
47) (h,k)=(0,1),(x,y)=(2,5)
- Answer
-
f(x)=x2+1
48) (h,k)=(2,3),(x,y)=(5,12)
49) (h,k)=(−5,3),(x,y)=(2,9)
- Answer
-
f(x)=649x2+6049x+29749
50) (h,k)=(3,2),(x,y)=(10,1)
51) (h,k)=(0,1),(x,y)=(1,0)
- Answer
-
f(x)=−x2+1
52) (h,k)=(1,0),(x,y)=(0,1)
Graphical
For the exercises 53-58, sketch a graph of the quadratic function and give the vertex, axis of symmetry, and intercepts.
53) f(x)=x2−2x
- Answer
-
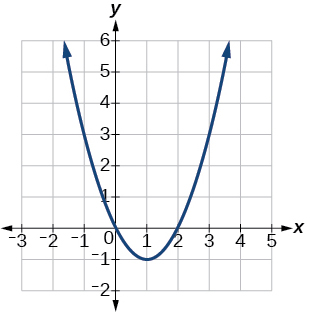
Vertex (1,−1), Axis of symmetry is x=1. Intercepts are (0,0),(2,0).
54) f(x)=x2−6x−1
55) f(x)=x2−5x−6
- Answer
-
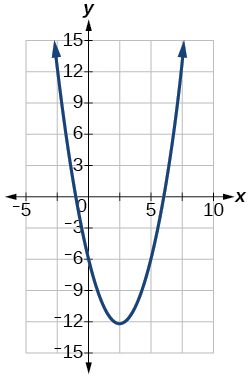
Vertex (52,−494), Axis of symmetry is x=52. Intercepts are (0,−6),(−1,0),(6,0).
56) f(x)=x2−7x+3
57) f(x)=−2x2+5x−8
- Answer
-
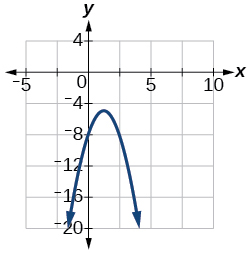
Vertex (54,−398), Axis of symmetry is x=54. Intercepts are (0,−8).
58) f(x)=4x2−12x−3
- Answer
-
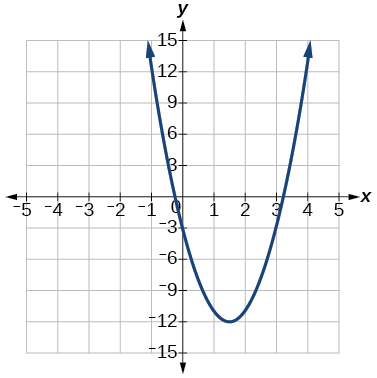
For the exercises 59-64, write the equation for the graphed function.
59)
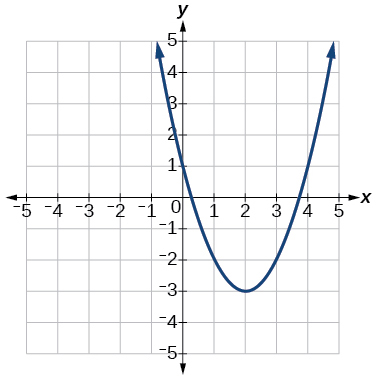
- Answer
-
f(x)=x2−4x+1
60)
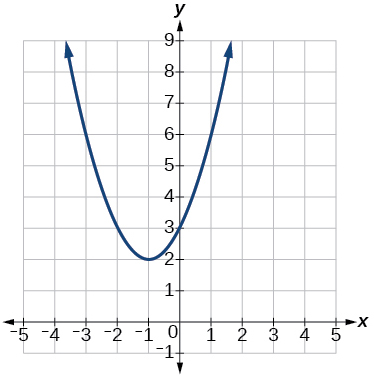
61)
- Answer
-
f(x)=−2x2+8x−1
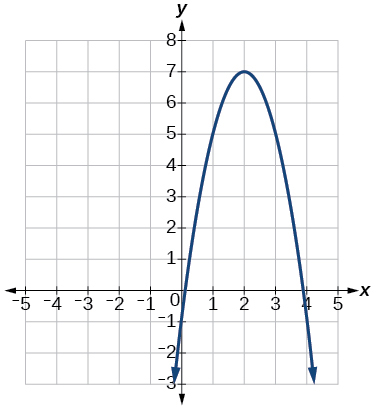
62)
63)

- Answer
-
f(x)=12x2−3x+72
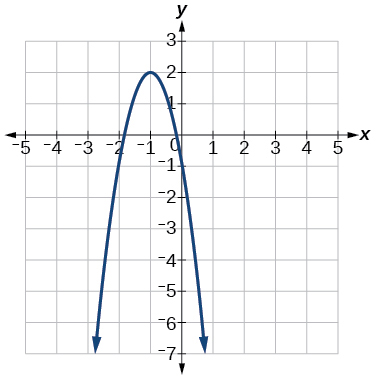
64)
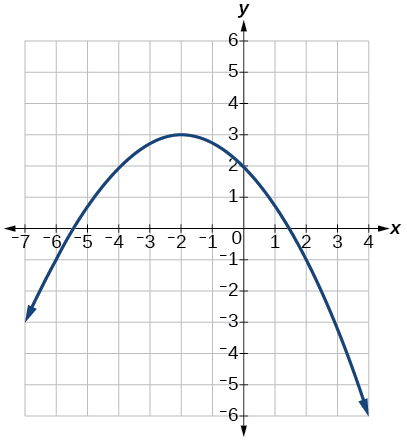
Numeric
For the exercises 65-69, use the table of values that represent points on the graph of a quadratic function. By determining the vertex and axis of symmetry, find the general form of the equation of the quadratic function.
65)
| x | –2 | –1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | 5 | 2 | 1 | 2 | 5 |
- Answer
-
f(x)=x2+1
66)
| x | –2 | –1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | 1 | 0 | 1 | 4 | 9 |
67)
| x | –2 | –1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | –2 | 1 | 2 | 1 | –2 |
- Answer
-
f(x)=2−x2
68)
| x | –2 | –1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | –8 | –3 | 0 | 1 | 0 |
69)
| x | –2 | –1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | 8 | 2 | 0 | 2 | 8 |
- Answer
-
f(x)=2x2
Technology
For the exercises 70-74, use a calculator to find the answer.
70) Graph on the same set of axes the functions f(x)=x2,f(x)=2x2, and f(x)=13x2. What appears to be the effect of changing the coefficient?
71) Graph on the same set of axes f(x)=x2,f(x)=x2+2 and f(x)=x2,f(x)=x2+5 and f(x)=x2−3. What appears to be the effect of adding a constant?
- Answer
-
The graph is shifted up or down (a vertical shift).
72) Graph on the same set of axes f(x)=x2,f(x)=(x−2)2,f(x−3)2, and f(x)=(x+4)2. What appears to be the effect of adding or subtracting those numbers?
73) The path of an object projected at a 45 degree angle with initial velocity of 80 feet per second is given by the function h(x)=−32(80)2x2+x where x is the horizontal distance traveled and h(x) is the height in feet. Use the TRACE feature of your calculator to determine the height of the object when it has traveled 100 feet away horizontally.
- Answer
-
50 feet
74) A suspension bridge can be modeled by the quadratic function h(x)=.0001x2 with −2000≤x≤2000 where |x| is the number of feet from the center and h(x) is height in feet. Use the TRACE feature of your calculator to estimate how far from the center does the bridge have a height of 100 feet.
Extensions
For the exercises 75-78, use the vertex of the graph of the quadratic function and the direction the graph opens to find the domain and range of the function.
75) Vertex (1,−2), opens up.
- Answer
-
Domain is (−∞,∞). Range is [−2,∞).
76) Vertex (−1,2) opens down.
77) Vertex (−5,11), opens down.
- Answer
-
Domain is (−∞,∞) Range is (−∞,11].
78) Vertex (−100,100), opens up.
For the exercises 79-84, write the equation of the quadratic function that contains the given point and has the same shape as the given function.
79) Contains (1,1) and has shape of f(x)=2x2. Vertex is on the y-axis.
- Answer
-
f(x)=2x2−1
80) Contains (−1,4) and has the shape of f(x)=2x2. Vertex is on the y-axis.
81) Contains (2,3) and has the shape of f(x)=3x2. Vertex is on the y-axis.
- Answer
-
f(x)=3x2−9
82) Contains (1,−3) and has the shape of f(x)=−x2. Vertex is on the y-axis.
83) Contains (4,3) and has the shape of f(x)=5x2. Vertex is on the y-axis.
- Answer
-
f(x)=5x2−77
84) Contains (1,−6) has the shape of f(x)=3x2. Vertex has x-coordinate of −1.
Real-World Applications
85) Find the dimensions of the rectangular corral producing the greatest enclosed area given 200 feet of fencing.
- Answer
-
50 feet by 50 feet. Maximize f(x)=−x2+100x.
86) Find the dimensions of the rectangular corral split into 2 pens of the same size producing the greatest possible enclosed area given 300 feet of fencing.
87) Find the dimensions of the rectangular corral producing the greatest enclosed area split into 3 pens of the same size given 500 feet of fencing.
- Answer
-
125 feet by 62.5 feet. Maximize f(x)=−2x2+250x.
88) Among all of the pairs of numbers whose sum is 6, find the pair with the largest product. What is the product?
89) Among all of the pairs of numbers whose difference is 12, find the pair with the smallest product. What is the product?
- Answer
-
6 and −6; product is −36; maximize f(x)=x2+12x.
90) Suppose that the price per unit in dollars of a cell phone production is modeled by p=$45−0.0125x, where x is in thousands of phones produced, and the revenue represented by thousands of dollars is R=x⋅p. Find the production level that will maximize revenue.
91) A rocket is launched in the air. Its height, in meters above sea level, as a function of time, in seconds, is given by h(t)=−4.9t2+229t+234. Find the maximum height the rocket attains.
- Answer
-
2909.56 meters
92) A ball is thrown in the air from the top of a building. Its height, in meters above ground, as a function of time, in seconds, is given by h(t)=−4.9t2+24t+8. How long does it take to reach maximum height?
93) A soccer stadium holds 62,000 spectators. With a ticket price of $11, the average attendance has been 26,000. When the price dropped to $9, the average attendance rose to 31,000. Assuming that attendance is linearly related to ticket price, what ticket price would maximize revenue?
- Answer
-
$10.70
94) A farmer finds that if she plants 75 trees per acre, each tree will yield 20 bushels of fruit. She estimates that for each additional tree planted per acre, the yield of each tree will decrease by 3 bushels. How many trees should she plant per acre to maximize her harvest?
3.3 Power Functions and Polynomial Functions
Verbal
1) Explain the difference between the coefficient of a power function and its degree.
- Answer
-
The coefficient of the power function is the real number that is multiplied by the variable raised to a power. The degree is the highest power appearing in the function.
2) If a polynomial function is in factored form, what would be a good first step in order to determine the degree of the function?
3) In general, explain the end behavior of a power function with odd degree if the leading coefficient is positive.
- Answer
-
As x decreases without bound, so does f(x). As x increases without bound, so does f(x).
4) What is the relationship between the degree of a polynomial function and the maximum number of turning points in its graph?
5) What can we conclude if, in general, the graph of a polynomial function exhibits the following end behavior? As x→−∞,f(x)→−∞ and as x→∞,f(x)→−∞.
- Answer
-
The polynomial function is of even degree and leading coefficient is negative.
Algebraic
For the exercises 6-11, identify the function as a power function, a polynomial function, or neither.
6) f(x)=x5
7) f(x)=(x2)3
- Answer
-
Power function
8) f(x)=x−x4
9) f(x)=x2x2−1
- Answer
-
Neither
10) f(x)=2x(x+2)(x−1)2
11) f(x)=3x+1
- Answer
-
Neither
For the exercises 12-16, find the degree and leading coefficient for the given polynomial.
12) −3x4
13) 7−2x2
- Answer
-
Degree = 2, Coefficient = −2
14) −2x2−3x5+x−6
15) x(4−x2)(2x+1)
- Answer
-
Degree =4, Coefficient = −2
16) x2(2x−3)2
For the exercises 17-24, determine the end behavior of the functions.
17) f(x)=x4
- Answer
-
As x→∞, f(x)→∞, as x→−∞, f(x)→∞
18) f(x)=x3
19) f(x)=−x4
- Answer
-
As x→−∞, f(x)→−∞, as x→∞, f(x)→−∞
20) f(x)=−x9
21) f(x)=−2x4−3x2+x−1
- Answer
-
As x→−∞, f(x)→−∞, as x→∞, f(x)→−∞
22) f(x)=3x2+x−2
23) f(x)=x2(2x3−x+1)
- Answer
-
As x→∞, f(x)→∞, as x→−∞, f(x)→−∞
24) f(x)=(2−x)7
For the exercises 25-30, find the intercepts of the functions.
25) f(t)=2(t−1)(t+2)(t−3)
- Answer
-
y-intercept is (0,12), t-intercepts are (1,0);(–2,0); and (3,0).
26) g(n)=−2(3n−1)(2n+1)
27) f(x)=x4−16
- Answer
-
y-intercept is (0,−16), x-intercepts are (2,0) and (−2,0).
28) f(x)=x3+27
29) f(x)=x(x2−2x−8)
- Answer
-
y-intercept is (0,0), x-intercepts are (0,0),(4,0), and (−2,0).
30) f(x)=(x+3)(4x2−1)
Graphical
For the exercises 31-38, determine the least possible degree of the polynomial function shown.
31)
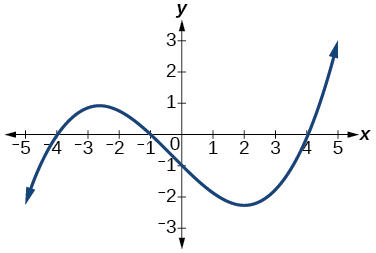
- Answer
-
3
32)
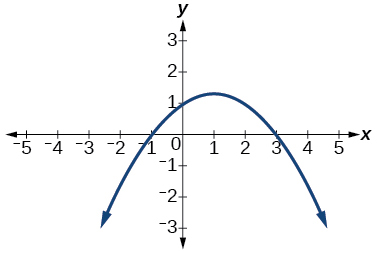
33)
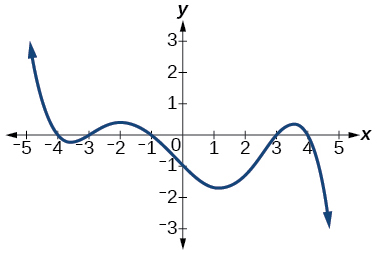
- Answer
-
5
34)
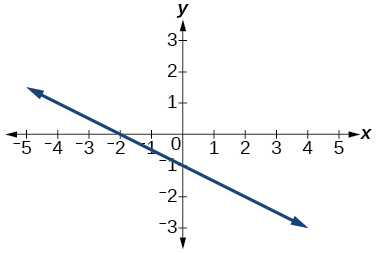
35)
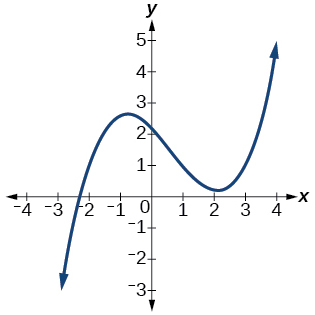
- Answer
-
3
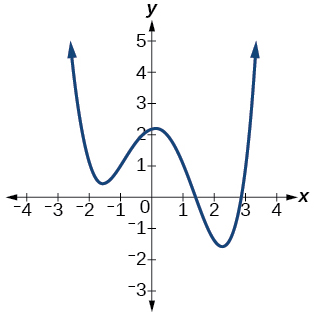
36)
37)
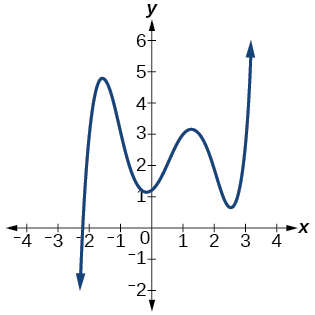
- Answer
-
5
38)
For the exercises 39-45, determine whether the graph of the function provided is a graph of a polynomial function. If so, determine the number of turning points and the least possible degree for the function.
39)
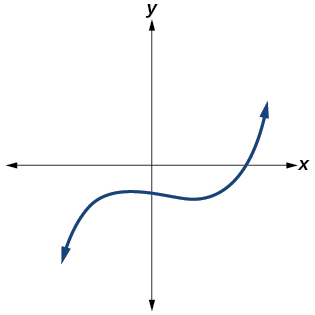
- Answer
-
Yes. Number of turning points is 2. Least possible degree is 3.
40)
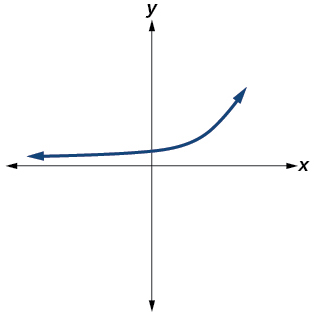
41)
- Answer
-
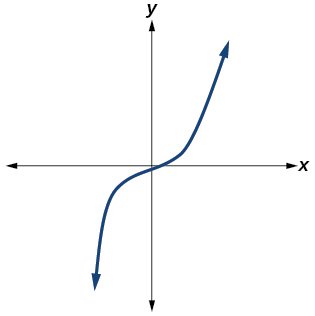
Yes. Number of turning points is 1. Least possible degree is 2.
42)
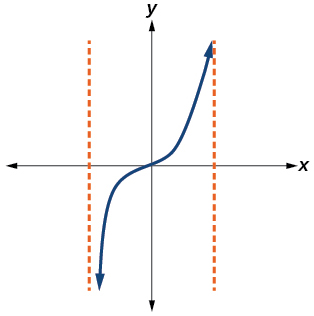
43)
- Answer
-
Yes. Number of turning points is 0. Least possible degree is 1.
44)
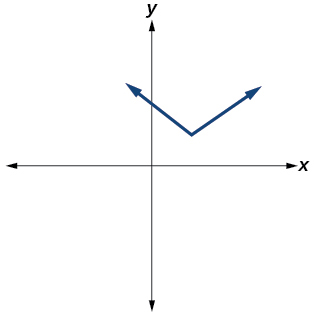
- Answer
-
No.
45)
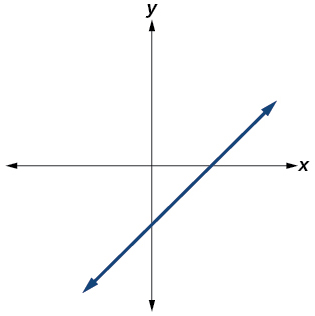
- Answer
-
Yes. Number of turning points is 0. Least possible degree is 1.
Numeric
For the exercises 46-50, make a table to confirm the end behavior of the function.
46) f(x)=−x3
47) f(x)=x4−5x2
- Answer
-
x f(x) 10 9,500 100 99,950,000 –10 9,500 –100 99,950,000 as x→−∞, f(x)→∞, as x→∞, f(x)→∞
48) f(x)=x2(1−x)2
49) f(x)=(x−1)(x−2)(3−x)
- Answer
-
x f(x) 10 –504 100 –941,094 –10 1,716 –100 1,061,106 as x→−∞, f(x)→∞, as x→∞, f(x)→−∞
50) f(x)=x510−x4
Technology
For the exercises 51-60, graph the polynomial functions using a calculator. Based on the graph, determine the intercepts and the end behavior.
51) f(x)=x3(x−2)
- Answer
-
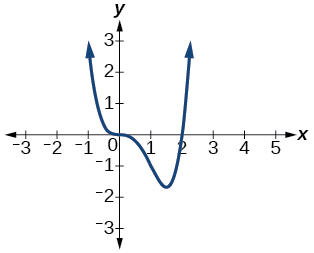
The y-intercept is (0,0). The x-intercepts are (0,0),(2,0). As x→−∞, f(x)→∞, as x→∞, f(x)→∞
52) f(x)=x(x−3)(x+3)
53) f(x)=x(14−2x)(10−2x)
- Answer
-
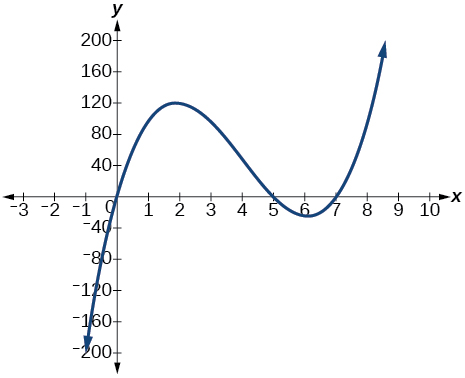
The y-intercept is (0,0). The x-intercepts are (0,0),(5,0),(7,0). As x→−∞, f(x)→−∞, as x→∞, f(x)→∞
54) f(x)=x(14−2x)(10−2x)2
55) f(x)=x3−16x
- Answer
-
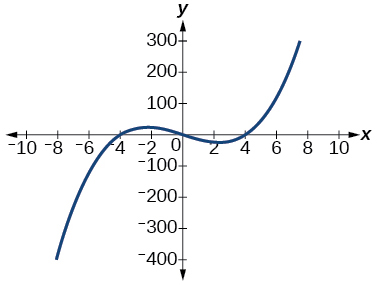
The y-intercept is (0,0). The x-intercept is (−4,0),(0,0),(4,0). As x→−∞, f(x)→−∞, as x→∞, f(x)→∞
56) f(x)=x3−27
57) f(x)=x4−81
- Answer
-
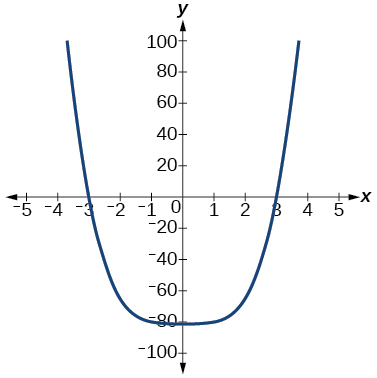
The y-intercept is (0,−81). The x-intercept are (3,0),(−3,0). As x→−∞, f(x)→∞, as x→∞, f(x)→∞
58) f(x)=−x3+x2+2x
59) f(x)=x3−2x2−15x
- Answer
-
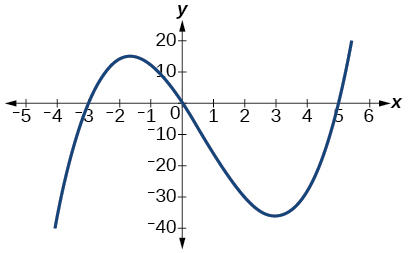
The y-intercept is (0,0). The x-intercepts are (−3,0),(0,0),(5,0). As x→−∞, f(x)→−∞, as x→∞, f(x)→∞
60) f(x)=x3−0.01x
Extensions
For the exercises 61-65, use the information about the graph of a polynomial function to determine the function. Assume the leading coefficient is 1 or −1. There may be more than one correct answer.
61) The y-intercept is (0,−4). The x-intercepts are (−2,0),(2,0). Degree is 2.
End behavior: as x→−∞, f(x)→∞, as x→∞, f(x)→∞.
- Answer
-
f(x)=x2−4
62) The y-intercept is (0,9). The x-intercepts are (−3,0),(3,0). Degree is 2.
End behavior: as x→−∞, f(x)→−∞, as x→∞, f(x)→−∞.
63) The y-intercept is (0,0). The x-intercepts are (0,0),(2,0). Degree is 3.
End behavior: as x→−∞, f(x)→−∞, as x→∞, f(x)→∞.
- Answer
-
f(x)=x^3−4x^2+4x
64) The y-intercept is (0,1). The x-intercept is (1,0). Degree is 3.
End behavior: as x→−∞, f(x)→∞, as x→∞, f(x)→−∞.
65) The y-intercept is (0,1). There is no x-intercept. Degree is 4.
End behavior: as x→−∞, f(x)→∞, as x→∞, f(x)→∞.
- Answer
-
f(x)=x^4+1
Real-World Applications
For the exercises 66-70, use the written statements to construct a polynomial function that represents the required information.
66) An oil slick is expanding as a circle. The radius of the circle is increasing at the rate of 20 meters per day. Express the area of the circle as a function of d, the number of days elapsed.
67) A cube has an edge of 3 feet. The edge is increasing at the rate of 2 feet per minute. Express the volume of the cube as a function of m, the number of minutes elapsed.
- Answer
-
V(m)=8m^3+36m^2+54m+27
68) A rectangle has a length of 10 inches and a width of 6 inches. If the length is increased by x inches and the width increased by twice that amount, express the area of the rectangle as a function of x.
69) An open box is to be constructed by cutting out square corners of x-inch sides from a piece of cardboard 8 inches by 8 inches and then folding up the sides. Express the volume of the box as a function of x.
- Answer
-
V(x)=4x^3−32x^2+64x
70) A rectangle is twice as long as it is wide. Squares of side 2 feet are cut out from each corner. Then the sides are folded up to make an open box. Express the volume of the box as a function of the width (x).
3.4 Graphs of Polynomial Functions
Verbal
1) What is the difference between an x-intercept and a zero of a polynomial function f?
- Answer
-
The x-intercept is where the graph of the function crosses the x-axis, and the zero of the function is the input value for which f(x)=0.
2) If a polynomial function of degree n has n distinct zeros, what do you know about the graph of the function?
3) Explain how the Intermediate Value Theorem can assist us in finding a zero of a function.
- Answer
-
If we evaluate the function at a and at b and the sign of the function value changes, then we know a zero exists between a and b.
4) Explain how the factored form of the polynomial helps us in graphing it.
5) If the graph of a polynomial just touches the x-axis and then changes direction, what can we conclude about the factored form of the polynomial?
- Answer
-
There will be a factor raised to an even power.
Algebraic
For the exercises 6-23, find the x-or t-intercepts of the polynomial functions.
6) C(t)=2(t−4)(t+1)(t−6)
7) C(t)=3(t+2)(t−3)(t+5)
- Answer
-
(−2,0),(3,0),(−5,0)
8) C(t)=4t(t−2)^2(t+1)
9) C(t)=2t(t−3)(t+1)^2
- Answer
-
(3,0),(−1,0),(0,0)
10) C(t)=2t^4−8t^3+6t^2
11) C(t)=4t^4+12t^3−40t^2
- Answer
-
(0,0), (−5,0), (2,0)
12) f(x)=x^4−x^2
13) f(x)=x^3+x^2−20x
- Answer
-
(0,0), (−5,0), (4,0)
14) f(x)=x^3+6x^2−7x
15) f(x)=x^3+x^2−4x−4
- Answer
-
(2,0), (−2,0), (−1,0)
16) f(x)=x^3+2x^2−9x−18
17) f(x)=2x^3−x^2−8x+4
- Answer
-
(−2,0),(2,0),\left(\dfrac{1}{2},0\right)
18) f(x)=x^6−7x^3−8
19) f(x)=2x^4+6x^2−8
- Answer
-
(1,0), (−1,0)
20) f(x)=x^3−3x^2−x+3
21) f(x)=x^6−2x^4−3x^2
- Answer
-
(0,0),(\sqrt{3},0),(−\sqrt{3},0)
22) f(x)=x^6−3x^4−4x^2
23) f(x)=x^5−5x^3+4x
- Answer
-
(0,0), (1,0), (−1,0), (2,0), (−2,0)
For the exercises 24-29, use the Intermediate Value Theorem to confirm that the given polynomial has at least one zero within the given interval.
24) f(x)=x^3−9x, between x=−4 and x=−2.
25) f(x)=x^3−9x, between x=2 and x=4.
- Answer
-
f(2)=–10 and f(4)=28. Sign change confirms.
26) f(x)=x^5−2x, between x=1 and x=2.
27) f(x)=−x^4+4, between x=1 and x=3.
- Answer
-
f(1)=3 and f(3)=–77. Sign change confirms.
28) f(x)=−2x^3−x, between x=–1 and x=1.
29) f(x)=x^3−100x+2, between x=0.01 and x=0.1
- Answer
-
f(0.01)=1.000001 and f(0.1)=–7.999. Sign change confirms.
For the exercises 30-41, find the zeros and give the multiplicity of each.
30) f(x)=(x+2)^3(x−3)^2
31) f(x)=x^2(2x+3)^5(x−4)^2
- Answer
-
0 with multiplicity 2, −\dfrac{3}{2} with multiplicity 5, 4 with multiplicity 2
32) f(x)=x^3(x−1)^3(x+2)
33) f(x)=x^2(x^2+4x+4)
- Answer
-
0 with multiplicity 2, -2 with multiplicity 2
34) f(x)=(2x+1)^3(9x^2−6x+1)
35) f(x)=(3x+2)^5(x^2−10x+25)
- Answer
-
−\dfrac{2}{3} with multiplicity 5, 5 with multiplicity 2
36) f(x)=x(4x^2−12x+9)(x^2+8x+16)
37) f(x)=x^6−x^5−2x^4
- Answer
-
0 with multiplicity 4, 2 with multiplicity 1, -1 with multiplicity 1
38) f(x)=3x^4+6x^3+3x^2
39) f(x)=4x^5−12x^4+9x^3
- Answer
-
\dfrac{3}{2} with multiplicity 2, 0 with multiplicity 3
40) f(x)=2x^4(x^3−4x^2+4x)
41) f(x)=4x^4(9x^4−12x^3+4x^2)
- Answer
-
0 with multiplicity 6, \dfrac{2}{3} with multiplicity 2
Graphical
For the exercises 42-47, graph the polynomial functions. Note x- and y- intercepts, multiplicity, and end behavior.
42) f(x)=(x+3)^2(x−2)
43) g(x)=(x+4)(x−1)^2
- Answer
-
x-intercepts, (1, 0) with multiplicity 2, (–4, 0) with multiplicity 1, y- intercept (0, 4). As x→−∞, f(x)→−∞, as x→∞, f(x)→∞.
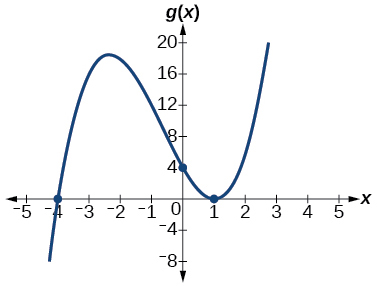
44) h(x)=(x−1)^3(x+3)^2
45) k(x)=(x−3)^3(x−2)^2
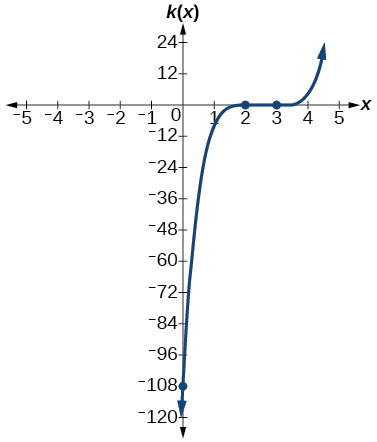
- Answer
-
x-intercepts (3,0) with multiplicity 3, (2,0) with multiplicity 2, y- intercept (0,–108). As x→−∞, f(x)→−∞, as x→∞, f(x)→∞.
46) m(x)=−2x(x−1)(x+3)
47) n(x)=−3x(x+2)(x−4)
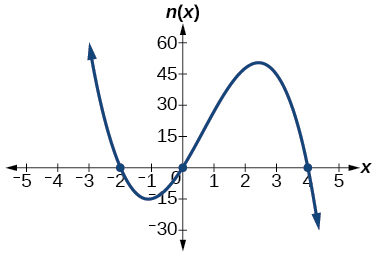
- Answer
-
x-intercepts (0, 0),(–2, 0),(4, 0) with multiplicity 1, y-intercept (0, 0). As x→−∞, f(x)→∞, as x→∞, f(x)→−∞.
For the exercises 48-52, use the graphs to write the formula for a polynomial function of least degree.
48)

49)
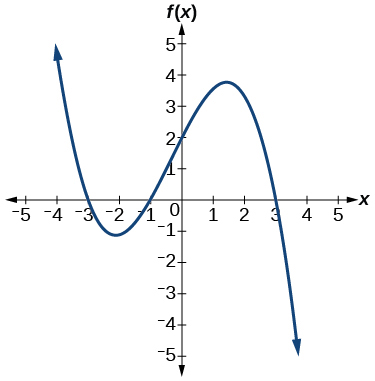
- Answer
-
f(x)=−\dfrac{2}{9}(x−3)(x+1)(x+3)
50)
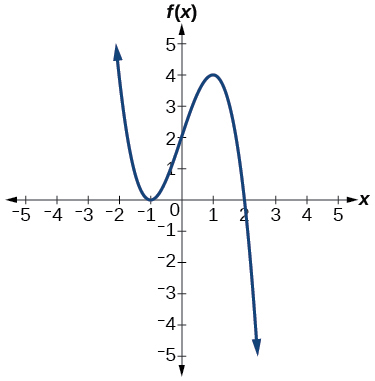
51)
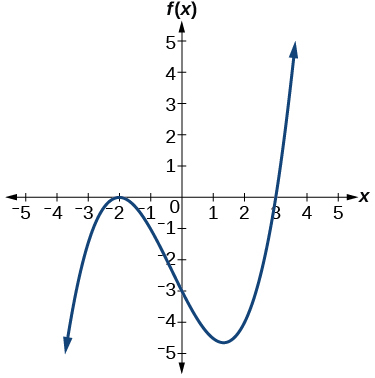
- Answer
-
f(x)=\dfrac{1}{4}(x+2)^2(x−3)
52)
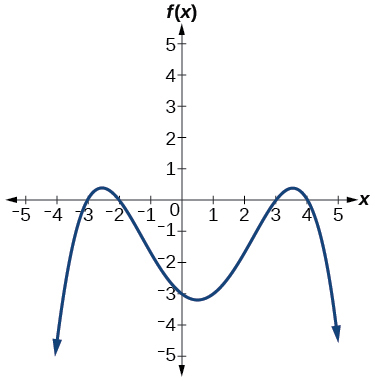
For the exercises 53-56, use the graph to identify zeros and multiplicity.
53)
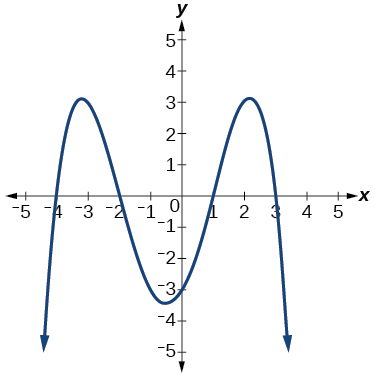
- Answer
-
–4, –2, 1, 3 with multiplicity 1
54)

55)
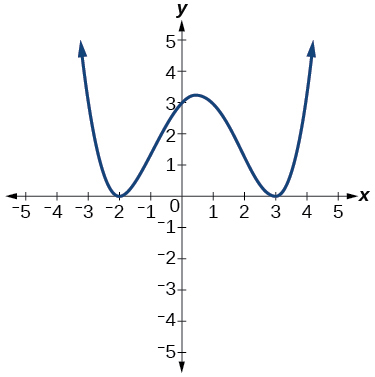
- Answer
-
–2, 3 each with multiplicity 2
56)
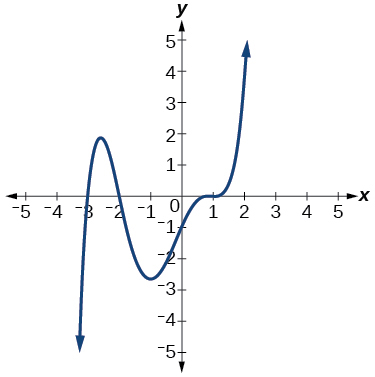
For the exercises 57-66, use the given information about the polynomial graph to write the equation.
57) Degree 3. Zeros at x=–2,x=1, and x=3. y-intercept at (0,–4)
- Answer
-
f(x)=−\dfrac{2}{3}(x+2)(x−1)(x−3)
58) Degree 3. Zeros at x=–5, x=–2, and x=1. y-intercept at (0,6)
59) Degree 5. Roots of multiplicity 2 at x=3 and x=1, and a root of multiplicity 1 at x=–3. y-intercept at (0,9)
- Answer
-
f(x)=\dfrac{1}{3}(x−3)^2(x−1)^2(x+3)
60) Degree 4. Root of multiplicity 2 at x=4, and a roots of multiplicity 1 at x=1 and x=–2. y-intercept at (0,–3)
61) Degree 5. Double zero at x=1, and triple zero at x=3. Passes through the point (2,15)
- Answer
-
f(x)=−15(x−1)^2(x−3)^3
62) Degree 3. Zeros at x=4, x=3, and x=2. y-intercept at (0,−24)
63) Degree 3. Zeros at x=−3, x=−2 and x=1. y-intercept at (0,12)
- Answer
-
f(x)=−2(x+3)(x+2)(x−1)
64) Degree 5. Roots of multiplicity 2 at x=−3 and x=2 and a root of multiplicity 1 at x=−2. y-intercept at (0, 4).
65) Degree 4. Roots of multiplicity 2 at x=\dfrac{1}{2} and roots of multiplicity 1 at x=6 and x=−2. y-intercept at (0,18)
- Answer
-
f(x)=−\dfrac{3}{2}(2x−1)^2(x−6)(x+2)
66) Double zero at x=−3 and triple zero at x=0. Passes through the point (1,32).
Technology
For the exercises 67-71, use a calculator to approximate local minima and maxima or the global minimum and maximum.
67) f(x)=x^3−x−1
- Answer
-
local max (–.58, –.62), local min (.58, –1.38)
68) f(x)=2x^3−3x−1
69) f(x)=x^4+x
- Answer
-
global min (–.63, –.47)
70) f(x)=−x^4+3x−2
71) f(x)=x^4−x^3+1
- Answer
-
global min (.75, .89)
Extensions
For the exercises 72-74, use the graphs to write a polynomial function of least degree.
72)
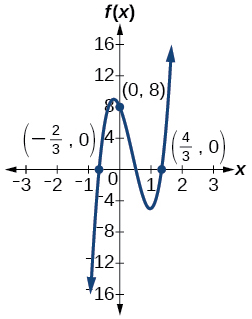
73)
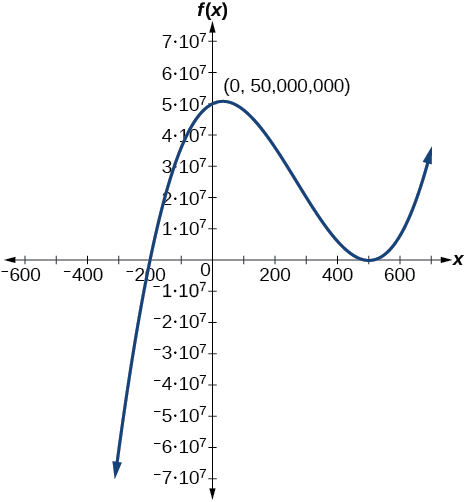
- Answer
-
f(x)=(x−500)^2(x+200)
74)
Real-World Applications
For the exercises 75-, write the polynomial function that models the given situation.
75) A rectangle has a length of 10 units and a width of 8 units. Squares of x by x units are cut out of each corner, and then the sides are folded up to create an open box. Express the volume of the box as a polynomial function in terms of x.
- Answer
-
f(x)=4x^3−36x^2+80x
76) Consider the same rectangle of the preceding problem. Squares of 2x by 2x units are cut out of each corner. Express the volume of the box as a polynomial in terms of x.
77) A square has sides of 12 units. Squares x +1 by x +1 units are cut out of each corner, and then the sides are folded up to create an open box. Express the volume of the box as a function in terms of x.
- Answer
-
f(x)=4x^3−36x^2+60x+100
78) A cylinder has a radius of x+2 units and a height of 3 units greater. Express the volume of the cylinder as a polynomial function.
79) A right circular cone has a radius of 3x+6 and a height 3 units less. Express the volume of the cone as a polynomial function. The volume of a cone is V=\dfrac{1}{3}πr^2h for radius r and height h.
- Answer
-
f(x)=π(9x^3+45x^2+72x+36)
3.5 Dividing Polynomials
Verbal
1) If division of a polynomial by a binomial results in a remainder of zero, what can be conclude?
- Answer
-
The binomial is a factor of the polynomial.
2) If a polynomial of degree n is divided by a binomial of degree 1, what is the degree of the quotient?
Algebraic
For the exercises 3-13, use long division to divide. Specify the quotient and the remainder.
3) (x^2+5x−1)÷(x−1)
- Answer
-
\mathrm{x+6+\dfrac{5}{x−1}, quotient: x+6, remainder: 5}
4) (2x^2−9x−5)÷(x−5)
5) (3x^2+23x+14)÷(x+7)
- Answer
-
\mathrm{3x+2, quotient: 3x+2, remainder: 0}
6) (4x^2−10x+6)÷(4x+2)
7) (6x^2−25x−25)÷(6x+5)
- Answer
-
\mathrm{x−5, quotient: x−5, remainder: 0}
8) (−x^2−1)÷(x+1)
9) (2x^2−3x+2)÷(x+2)
- Answer
-
\mathrm{2x−7+\dfrac{16}{x+2}, quotient: 2x−7, remainder: 16}
10) (x^3−126)÷(x−5)
11) (3x^2−5x+4)÷(3x+1)
- Answer
-
\mathrm{x−2+\dfrac{6}{3x+1}, quotient: x−2, remainder: 6}
12) (x^3−3x^2+5x−6)÷(x−2)
13) (2x^3+3x^2−4x+15)÷(x+3)
- Answer
-
\mathrm{2x^2−3x+5, quotient: 2x^2−3x+5, remainder: 0}
For the exercises 14-37, use synthetic division to find the quotient.
14) (3x^3−2x^2+x−4)÷(x+3)
15) (2x^3−6x^2−7x+6)÷(x−4)
- Answer
-
2x^2+2x+1+\dfrac{10}{x−4}
16) (6x^3−10x^2−7x−15)÷(x+1)
17) (4x^3−12x^2−5x−1)÷(2x+1)
- Answer
-
2x^2−7x+1−\dfrac{2}{2x+1}
18) (9x^3−9x^2+18x+5)÷(3x−1)
19) (3x^3−2x^2+x−4)÷(x+3)
- Answer
-
3x^2−11x+34−\dfrac{106}{x+3}
20) (−6x^3+x^2−4)÷(2x−3)
21) (2x^3+7x^2−13x−3)÷(2x−3)
- Answer
-
x^2+5x+1
22) (3x^3−5x^2+2x+3)÷(x+2)
23) (4x^3−5x^2+13)÷(x+4)
- Answer
-
4x^2−21x+84−\dfrac{323}{x+4}
24) (x^3−3x+2)÷(x+2)
25) (x^3−21x^2+147x−343)÷(x−7)
- Answer
-
x^2−14x+49
26) (x^3−15x^2+75x−125)÷(x−5)
27) (9x^3−x+2)÷(3x−1)
- Answer
-
3x^2+x+\dfrac{2}{3x−1}
28) (6x^3−x^2+5x+2)÷(3x+1)
29) (x^4+x^3−3x^2−2x+1)÷(x+1)
- Answer
-
x^3−3x+1
30) (x^4−3x^2+1)÷(x−1)
31) (x^4+2x^3−3x^2+2x+6)÷(x+3)
- Answer
-
x^3−x^2+2
32) (x^4−10x^3+37x^2−60x+36)÷(x−2)
33) (x^4−8x^3+24x^2−32x+16)÷(x−2)
- Answer
-
x^3−6x^2+12x−8
34) (x^4+5x^3−3x^2−13x+10)÷(x+5)
35) (x^4−12x^3+54x^2−108x+81)÷(x−3)
- Answer
-
x^3−9x^2+27x−27
36) (4x^4−2x^3−4x+2)÷(2x−1)
37) (4x^4+2x^3−4x^2+2x+2)÷(2x+1)
- Answer
-
2x^3−2x+2
For the exercises 38-43, use synthetic division to determine whether the first expression is a factor of the second. If it is, indicate the factorization.
38) x−2, 4x^3−3x^2−8x+4
39) x−2, 3x^4−6x^3−5x+10
- Answer
-
Yes (x−2)(3x^3−5)
40) x+3, −4x^3+5x^2+8
41) x−2, 4x^4−15x^2−4
- Answer
-
Yes (x−2)(4x^3+8x^2+x+2)
42) x−\dfrac{1}{2}, 2x^4−x^3+2x−1
43) x+\dfrac{1}{3}, 3x^4+x^3−3x+1
- Answer
-
No
Graphical
For the exercises 44-48, use the graph of the third-degree polynomial and one factor to write the factored form of the polynomial suggested by the graph. The leading coefficient is one.
44) Factor is x^2−x+3
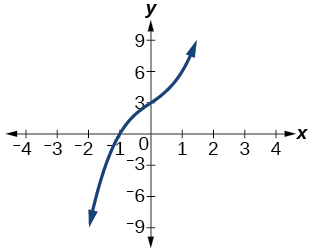
45) Factor is (x^2+2x+4)
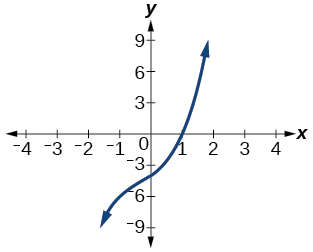
- Answer
-
(x−1)(x^2+2x+4)
46) Factor is x^2+2x+5
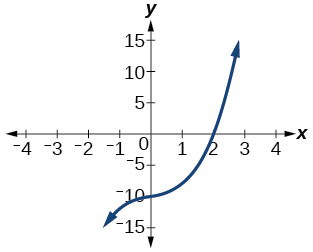
47) Factor is x^2+x+1
- Answer
-
(x−5)(x^2+x+1)
48) Factor is x^2+2x+2
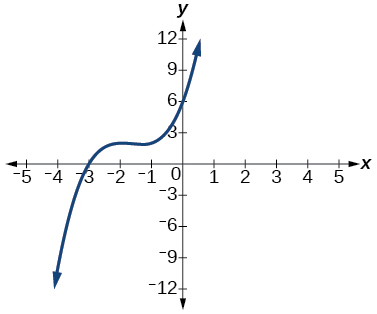
For the exercises 49-53, use synthetic division to find the quotient and remainder.
49) \dfrac{4x^3−33}{x−2}
- Answer
-
\mathrm{Quotient: 4x^2+8x+16, remainder: −1}
50) \dfrac{2x^3+25}{x+3}
51) \dfrac{3x^3+2x−5}{x−1}
- Answer
-
\mathrm{Quotient: 3x^2+3x+5, remainder: 0}
52) \dfrac{−4x^3−x^2−12}{x+4}
53) \dfrac{x^4−22}{x+2}
- Answer
-
\mathrm{Quotient: x^3−2x^2+4x−8, remainder: −6}
Technology
For the exercises 54-58, use a calculator with CAS to answer the questions.
54) Consider \dfrac{x^k−1}{x−1} with k=1, 2, 3. What do you expect the result to be if k=4?
55) Consider \dfrac{x^k+1}{x+1} for k=1, 3, 5. What do you expect the result to be if k=7?
- Answer
-
x^6−x^5+x^4−x^3+x^2−x+1
56) Consider \dfrac{x^4−k^4}{x−k} for k=1, 2, 3. What do you expect the result to be if k=4?
57) Consider \dfrac{x^k}{x+1} with k=1, 2, 3. What do you expect the result to be if k=4?
- Answer
-
x^3−x^2+x−1+\dfrac{1}{x+1}
58) Consider \dfrac{x^k}{x−1} with k=1, 2, 3. What do you expect the result to be if k=4?
Extensions
For the exercises 59-63, use synthetic division to determine the quotient involving a complex number.
59) \dfrac{x+1}{x−i}
- Answer
-
1+\dfrac{1+i}{x−i}
60) \dfrac{x^2+1}{x−i}
61) \dfrac{x+1}{x+i}
- Answer
-
1+\dfrac{1−i}{x+i}
62) \dfrac{x^2+1}{x+i}
63) \dfrac{x^3+1}{x−i}
- Answer
-
x^2−ix−1+\dfrac{1−i}{x−i}
Real-World Applications
For the exercises 64-66, use the given length and area of a rectangle to express the width algebraically.
64) Length is x+5, area is 2x^2+9x−5.
65) Length is 2x + 5, area is 4x^3+10x^2+6x+15.
- Answer
-
2x^2+3
66) Length is 3x–4, area is 6x^4−8x^3+9x^2−9x−4.
For the exercises 67-70, use the given volume of a box and its length and width to express the height of the box algebraically.
67) Volume is 12x^3+20x^2−21x−36, length is 2x+3, width is 3x−4.
- Answer
-
2x+3
68) Volume is 18x^3−21x^2−40x+48, length is 3x–4, width is 3x–4.
69) Volume is 10x^3+27x^2+2x−24, length is 5x–4, width is 2x+3.
- Answer
-
x+2
70) Volume is 10x^3+30x^2−8x−24, length is 2, width is x+3.
For the exercises 71-73, use the given volume and radius of a cylinder to express the height of the cylinder algebraically.
71) Volume is π(25x^3−65x^2−29x−3), radius is 5x+1.
- Answer
-
x−3
72) Volume is π(4x^3+12x^2−15x−50), radius is 2x+5.
73) Volume is π(3x^4+24x^3+46x^2−16x−32), radius is x+4.
- Answer
-
3x^2−2
3.6 Zeros of Polynomial Functions
Verbal
1) Describe a use for the Remainder Theorem.
- Answer
-
The theorem can be used to evaluate a polynomial.
2) Explain why the Rational Zero Theorem does not guarantee finding zeros of a polynomial function.
3) What is the difference between rational and real zeros?
- Answer
-
Rational zeros can be expressed as fractions whereas real zeros include irrational numbers.
4) If Descartes’ Rule of Signs reveals a no change of signs or one sign of changes, what specific conclusion can be drawn?
5) If synthetic division reveals a zero, why should we try that value again as a possible solution?
- Answer
-
Polynomial functions can have repeated zeros, so the fact that number is a zero doesn’t preclude it being a zero again.
Algebraic
For the exercises 6-13, use the Remainder Theorem to find the remainder.
6) (x^4−9x^2+14)÷(x−2)
7) (3x^3−2x^2+x−4)÷(x+3)
- Answer
-
−106
8) (x^4+5x^3−4x−17)÷(x+1)
9) (−3x^2+6x+24)÷(x−4)
- Answer
-
0
10) (5x^5−4x^4+3x^3−2x^2+x−1)÷(x+6)
11) (x^4−1)÷(x−4)
- Answer
-
255
12) (3x^3+4x^2−8x+2)÷(x−3)
13) (4x^3+5x^2−2x+7)÷(x+2)
- Answer
-
−1
For the exercises 14-21, use the Factor Theorem to find all real zeros for the given polynomial function and one factor.
14) f(x)=2x^3−9x^2+13x−6; x−1
15) f(x)=2x^3+x^2−5x+2; x+2
- Answer
-
−2, 1, \dfrac{1}{2}
16) f(x)=3x^3+x^2−20x+12; x+3
17) f(x)=2x^3+3x^2+x+6;x+2
- Answer
-
−2
18) f(x)=−5x^3+16x^2−9;x−3
19) x^3+3x^2+4x+12;x+3
- Answer
-
−3
20) 4x^3−7x+3;x−1
21) 2x^3+5x^2−12x−30,2x+5
- Answer
-
−\dfrac{5}{2}, \sqrt{6}, −\sqrt{6}
For the exercises 22-39, use the Rational Zero Theorem to find all real zeros.
22) x^3−3x^2−10x+24=0
23) 2x^3+7x^2−10x−24=0
- Answer
-
2, −4, −\dfrac{3}{2}
24) x^3+2x^2−9x−18=0
25) x^3+5x^2−16x−80=0
- Answer
-
4, −4, −5
26) x^3−3x^2−25x+75=0
27) 2x^3−3x^2−32x−15=0
- Answer
-
5, −3, −\dfrac{1}{2}
28) 2x^3+x^2−7x−6=0
29) 2x^3−3x^2−x+1=0
- Answer
-
\dfrac{1}{2}, \dfrac{1+\sqrt{5}}{2}, \dfrac{1−\sqrt{5}}{2}
30) 3x^3−x^2−11x−6=0
31) 2x^3−5x^2+9x−9=0
- Answer
-
\dfrac{3}{2}
32) 2x^3−3x^2+4x+3=0
33) x^4−2x^3−7x^2+8x+12=0
- Answer
-
2, 3, −1, −2
34) x^4+2x^3−9x^2−2x+8=0
35) 4x^4+4x^3−25x^2−x+6=0
- Answer
-
\dfrac{1}{2}, −\dfrac{1}{2}, 2, −3
36) 2x^4−3x^3−15x^2+32x−12=0
37) x^4+2x^3−4x^2−10x−5=0
- Answer
-
−1, −1, \sqrt{5}, −\sqrt{5}
38) 4x^3−3x+1=0
39) 8x^4+26x^3+39x^2+26x+6
- Answer
-
−\dfrac{3}{4}, −\dfrac{1}{2}
For the exercises 40-45, find all complex solutions (real and non-real).
40) x^3+x^2+x+1=0
41) x^3−8x^2+25x−26=0
- Answer
-
2, 3+2i, 3−2i
42) x^3+13x^2+57x+85=0
43) 3x^3−4x^2+11x+10=0
- Answer
-
−\dfrac{2}{3}, 1+2i, 1−2i
44) x^4+2x^3+22x^2+50x−75=0
45) 2x^3−3x^2+32x+17=0
- Answer
-
−\dfrac{1}{2}, 1+4i, 1−4i
Graphical
For the exercises 46-55, use Descartes’ Rule to determine the possible number of positive and negative solutions. Confirm with the given graph.
46) f(x)=x^3−1
47) f(x)=x^4−x^2−1
- Answer
-
1 positive, 1 negative
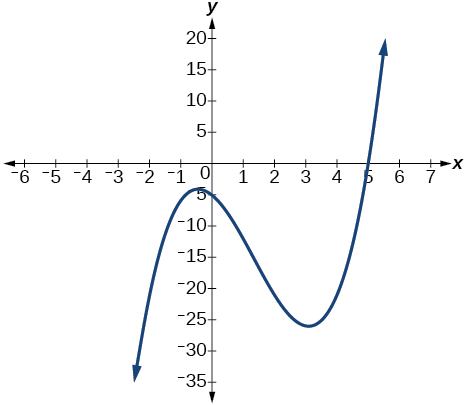
48) f(x)=x^3−2x^2−5x+6
49) f(x)=x^3−2x^2+x−1
- Answer
-
3 or 1 positive, 0 negative
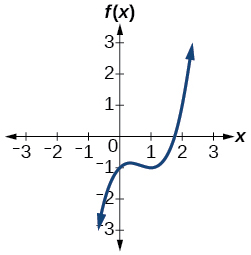
50) f(x)=x^4+2x^3−12x^2+14x−5
51) f(x)=2x^3+37x^2+200x+300
- Answer
-
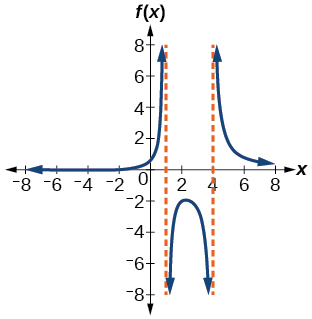
0 positive, 3 or 1 negative
.jpg?revision=1)
52) f(x)=x^3−2x^2−16x+32
53) f(x)=2x^4−5x^3−5x^2+5x+3
- Answer
-
2 or 0 positive, 2 or 0 negative
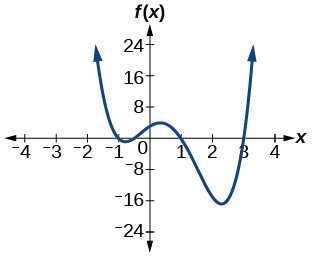
54) f(x)=2x^4−5x^3−14x^2+20x+8
55) f(x)=10x^4−21x^2+11
- Answer
-
2 or 0 positive, 2 or 0 negative
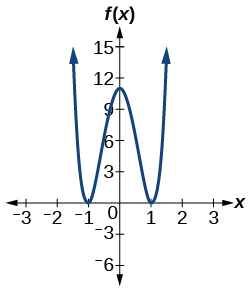
Numeric
For the exercises 56-60, list all possible rational zeros for the functions.
56) f(x)=x^4+3x^3−4x+4
57) f(x)=2x^3+3x^2−8x+5
- Answer
-
±5, ±1, ± \dfrac{5}{2}
58) f(x)=3x^3+5x^2−5x+4
59) f(x)=6x^4−10x^2+13x+1
- Answer
-
±1, ±\dfrac{1}{2}, ±\dfrac{1}{3}, ±\dfrac{1}{6}
60) f(x)=4x^5−10x^4+8x^3+x^2−8
Technology
For the exercises 61-65, use your calculator to graph the polynomial function. Based on the graph, find the rational zeros. All real solutions are rational.
61) f(x)=6x^3−7x^2+1
- Answer
-
1, \dfrac{1}{2}, −\dfrac{1}{3}
62) f(x)=4x^3−4x^2−13x−5
63) f(x)=8x^3−6x^2−23x+6
- Answer
-
2, \dfrac{1}{4}, −\dfrac{3}{2}
64) f(x)=12x^4+55x^3+12x^2−117x+54
65) f(x)=16x^4−24x^3+x^2−15x+25
- Answer
-
\dfrac{5}{4}
Extensions
For the exercises 66-70, construct a polynomial function of least degree possible using the given information.
66) Real roots: –1, 1, 3 and (2,f(2))=(2,4)
67) Real roots: –1 (with multiplicity 2 and 1) and (2,f(2))=(2,4)
- Answer
-
f(x)=\dfrac{4}{9}(x^3+x^2−x−1)
68) Real roots: –2, \dfrac{1}{2} (with multiplicity 2) and (−3,f(−3))=(−3,5)
69) Real roots:−\dfrac{1}{2}, 0,\dfrac{1}{2} and (−2,f(−2))=(−2,6)
- Answer
-
f(x)=−\dfrac{1}{5}(4x^3−x)
70) Real roots: –4, –1, 1, 4 and (−2,f(−2))=(−2,10)
Real-World Applications
For the exercises 71-75, find the dimensions of the box described.
71) The length is twice as long as the width. The height is 2 inches greater than the width. The volume is 192 cubic inches.
- Answer
-
8 by 4 by 6 inches
72) The length, width, and height are consecutive whole numbers. The volume is 120 cubic inches.
73) The length is one inch more than the width, which is one inch more than the height. The volume is 86.625 cubic inches.
- Answer
-
5.5 by 4.5 by 3.5 inches
74) The length is three times the height and the height is one inch less than the width. The volume is 108 cubic inches.
75) The length is 3 inches more than the width. The width is 2 inches more than the height. The volume is 120 cubic inches.
- Answer
-
8 by 5 by 3 inches
For the exercises 76-80, find the dimensions of the right circular cylinder described.
76) The radius is 3 inches more than the height. The volume is 16π cubic meters.
77) The height is one less than one half the radius. The volume is 72π cubic meters.
- Answer
-
Radius = 6 meters, Height = 2 meters
78) The radius and height differ by one meter. The radius is larger and the volume is 48π cubic meters.
79) The radius and height differ by two meters. The height is greater and the volume is 28.125π cubic meters.
- Answer
-
Radius = 2.5 meters, Height = 4.5 meters
80) The radius is \dfrac{1}{3} meter greater than the height. The volume is \dfrac{98}{9}π cubic meters.
3.7 Rational Functions
Verbal
1) What is the fundamental difference in the algebraic representation of a polynomial function and a rational function?
- Answer
-
The rational function will be represented by a quotient of polynomial functions.
2) What is the fundamental difference in the graphs of polynomial functions and rational functions?
3) If the graph of a rational function has a removable discontinuity, what must be true of the functional rule?
- Answer
-
The numerator and denominator must have a common factor.
4) Can a graph of a rational function have no vertical asymptote? If so, how?
5) Can a graph of a rational function have no x-intercepts? If so, how?
- Answer
-
Yes. The numerator of the formula of the functions would have only complex roots and/or factors common to both the numerator and denominator.
Algebraic
For the exercises 6-9, find the domain of the rational functions.
6) f(x)=\dfrac{x-1}{x+2}
7) f(x)=\dfrac{x+1}{x^{2}-1}
- Answer
-
All reals x \neq -1,1
8) f(x)=\dfrac{x^{2}+4}{x^{2}-2 x-8}
9) f(x)=\dfrac{x^{2}+4 x-3}{x^{4}-5 x^{2}+4}
- Answer
-
All reals x \neq-1,-2,1,2
For the exercises 10-19, find the domain, vertical asymptotes, and horizontal asymptotes of the functions.
10) f(x)=\dfrac{4}{x-1}
11) f(x)=\dfrac{2}{5 x+2}
- Answer
-
V.A. at x=-\dfrac{2}{5}; H.A. at y=0; Domain is all reals x \neq-\dfrac{2}{5}
12) f(x)=\dfrac{x}{x^{2}-9}
13) f(x)=\dfrac{x}{x^{2}+5 x-36}
- Answer
-
V.A. at x=4,-9; H.A. at y=0; Domain is all reals x \neq 4,-9
14) f(x)=\dfrac{3+x}{x^{3}-27}
15) f(x)=\dfrac{3x-4}{x^{3}-16x}
- Answer
-
V.A. at x=0,4,-4; H.A. at y=0; Domain is all reals x \neq 0,4,-4
16) f(x)=\dfrac{x^{2}-1}{x^{3}+9 x^{2}+14 x}
17) f(x)=\dfrac{x+5}{x^{2}-25}
- Answer
-
V.A. at x=-5; H.A. at y=0; Domain is all reals x \neq 5,-5
18) f(x)=\dfrac{x-4}{x-6}
19) f(x)=\dfrac{4-2x}{3 x-1}
- Answer
-
V.A. at x=\dfrac{1}{3}; H.A. at y=-\dfrac{2}{3}; Domain is all reals x \neq \dfrac{1}{3}
For the exercises 20-24, find the x- and y-intercepts for the functions.
20) f(x)=\dfrac{x+5}{x^{2}+4}
21) f(x)=\dfrac{x}{x^{2}-x}
- Answer
-
none
22) f(x)=\dfrac{x^{2}+8 x+7}{x^{2}+11 x+30}
23) f(x)=\dfrac{x^{2}+x+6}{x^{2}-10 x+24}
- Answer
-
x -intercepts none, y -intercept \left(0, \dfrac{1}{4}\right)
24) f(x)=\dfrac{94-2 x^{2}}{3 x^{2}-12}
For the exercises 25-29, describe the local and end behavior of the functions.
25) f(x)=\dfrac{x}{2 x+1}
- Answer
-
Local behavior: x \rightarrow-\dfrac{1}{2}^{+}, f(x) \rightarrow-\infty, x \rightarrow-\dfrac{1}{2}^{-}, f(x) \rightarrow \infty
End behavior: x \rightarrow \pm \infty, f(x) \rightarrow \dfrac{1}{2}
26) f(x)=\dfrac{2x}{x-6}
27) f(x)=\dfrac{-2x}{x-6}
- Answer
-
Local behavior: x \rightarrow 6^{+}, f(x) \rightarrow-\infty, x \rightarrow 6^{-}, f(x) \rightarrow \infty
End behavior: x \rightarrow \pm \infty, f(x) \rightarrow-2
28) f(x)=\dfrac{x^{2}-4 x+3}{x^{2}-4x-5}
29) f(x)=\dfrac{2 x^{2}-32}{6 x^{2}+13x-5}
- Answer
-
Local behavior: x \rightarrow-\dfrac{1}{3}, f(x) \rightarrow \infty, x \rightarrow-\dfrac{1}{3}, f(x) \rightarrow-\infty, x \rightarrow \dfrac{5}{2}, f(x) \rightarrow \infty, x \rightarrow \dfrac{5}{2}+f(x) \rightarrow-\infty
End behavior: x \rightarrow \pm \infty, f(x) \rightarrow \dfrac{1}{3}
For the exercises 30-34, find the slant asymptote of the functions.
30) f(x)=\dfrac{24 x^{2}+6 x}{2 x+1}
31) f(x)=\dfrac{4 x^{2}-10}{2 x-4}
- Answer
-
y=2 x+4
32) f(x)=\dfrac{81 x^{2}-18}{3 x-2}
33) f(x)=\dfrac{6 x^{3}-5 x}{3 x^{2}+4}
- Answer
-
y=2 x
34) f(x)=\dfrac{x^{2}+5x+4}{x-1}
Graphical
For the exercises 35-38, use the given transformation to graph the function. Note the vertical and horizontal asymptotes.
35) The reciprocal function shifted up two units.
- Answer
-
V.A. x=0, H.A. y=2
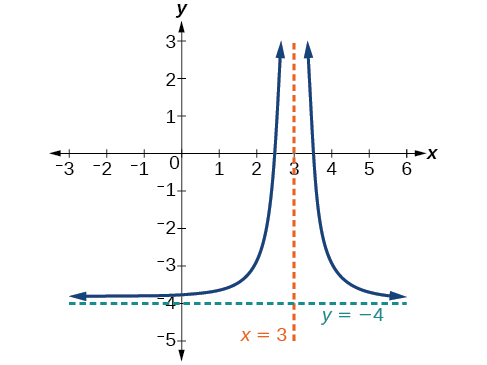
36) The reciprocal function shifted down one unit and left three units.
37) The reciprocal squared function shifted to the right 2 units.
- Answer
-
V.A. x=2, H.A. y=0
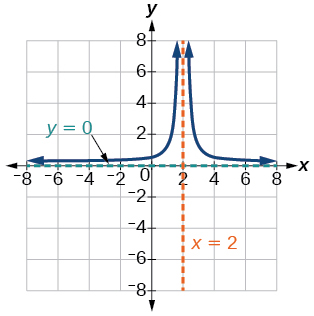
38) The reciprocal squared function shifted down 2 units and right 1 unit.
For the exercises 39-50, find the horizontal intercepts, the vertical intercept, the vertical asymptotes, and the horizontal or slant asymptote of the functions. Use that information to sketch a graph.
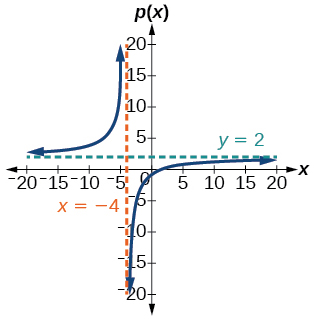
39) p(x)=\dfrac{2x-3}{x+4}
- Answer
-
V.A. x=-4, H.A. y=2; \left(\dfrac{3}{2}, 0\right); \left(0,-\dfrac{3}{4}\right)
40) q(x)=\dfrac{x-5}{3 x-1}
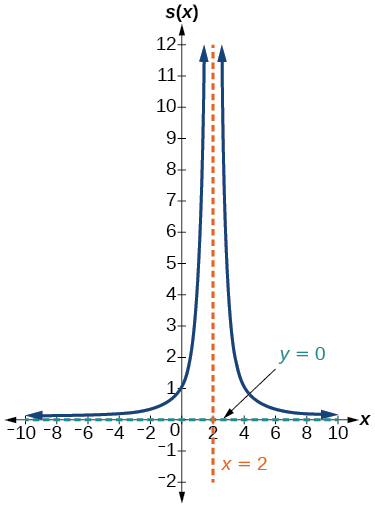
41) s(x)=\dfrac{4}{(x-2)^{2}}
- Answer
-
V.A. x=2, H.A. y=0, (0,1)
42) r(x)=\dfrac{5}{(x+1)^{2}}
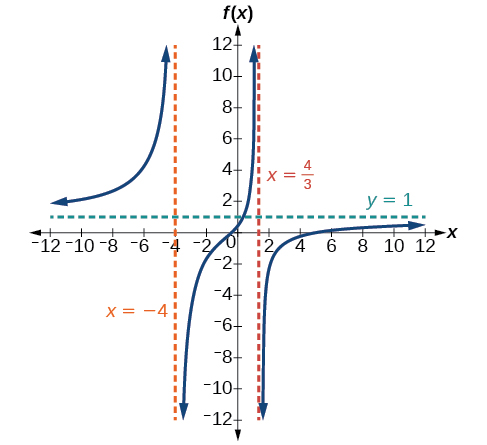
43) f(x)=\dfrac{3 x^{2}-14 x-5}{3 x^{2}+8 x-16}
- Answer
-
V.A. x=-4, x=\dfrac{4}{3}, H.A. y=1; (5,0); \left(-\dfrac{1}{3}, 0\right); \left(0, \dfrac{5}{16}\right)
44) g(x)=\dfrac{2 x^{2}+7 x-15}{3 x^{2}-14+15}
45) a(x)=\dfrac{x^{2}+2 x-3}{x^{2}-1}
- Answer
-
V.A. x=−1, H.A. y=1; (−3,0); (0,3)
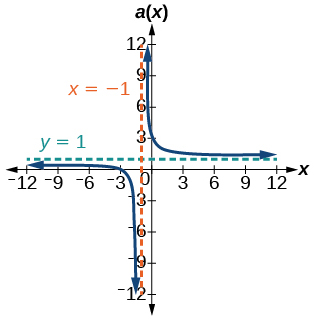
46) b(x)=\dfrac{x^{2}-x-6}{x^{2}-4}
47) h(x)=\dfrac{2 x^{2}+x-1}{x-4}
- Answer
-
V.A. x=4, S.A. y=2x+9; (-1,0); \left(\dfrac{1}{2}, 0\right); \left(0, \dfrac{1}{4}\right)
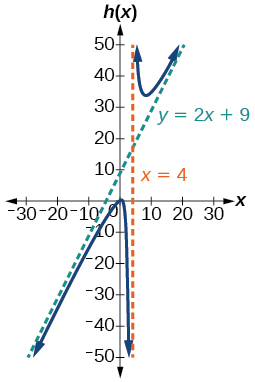
48) k(x)=\dfrac{2 x^{2}-3 x-20}{x-5}
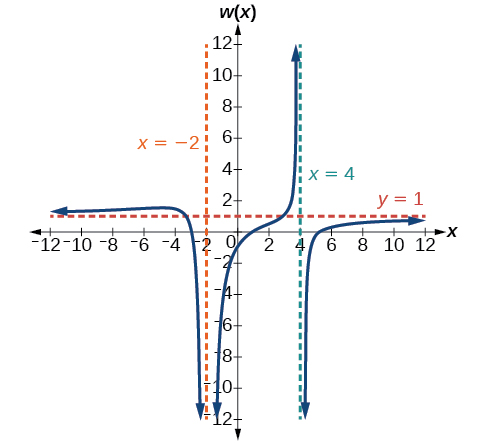
49) w(x)=\dfrac{(x-1)(x+3)(x-5)}{(x+2)^{2}(x-4)}
- Answer
-
V.A. x=-2, x=4, H.A. y=1, (1,0); (5,0); (-3,0); \left(0,-\dfrac{15}{16}\right)
50) z(x)=\dfrac{(x+2)^{2}(x-5)}{(x-3)(x+1)(x+4)}
For the exercises 51-56, write an equation for a rational function with the given characteristics.
51) Vertical asymptotes at x=5, x -intercepts at (2,0) and (-1,0), y -intercept at (0,4)
- Answer
-
y=50 \dfrac{x^{2}-x-2}{x^{2}-25}
52) Vertical asymptotes at x=-4 and x=-1, x -intercepts at (1,0) and (5,0), y -intercept at (0,7)
53) Vertical asymptotes at x=-4 and x=-5, x -intercepts at (4,0) and (-6,0), Horizontal asymptote at y=7
- Answer
-
y=7 \dfrac{x^{2}+2 x-24}{x^{2}+9 x+20}
54) Vertical asymptotes at x=-3 and x=6, x -intercepts at (-2,0) and (1,0), Horizontal asymptote at y=-2
55) Vertical asymptote at x=-1, Double zero at x=2, y -intercept at (0,2)
- Answer
-
y=\dfrac{1}{2} \dfrac{x^{2}-4 x+4}{x+1}
56) Vertical asymptote at x=3, Double zero at x=1, y -intercept at (0,4)
For the exercises 57-,64 use the graphs to write an equation for the function.
57)
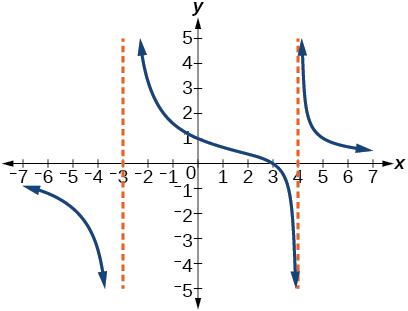
- Answer
-
y=4 \dfrac{x-3}{x^{2}-x-12}
58)
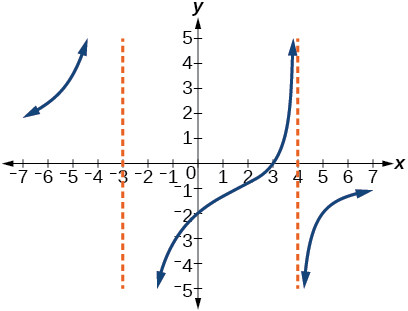
59)
- Answer
-
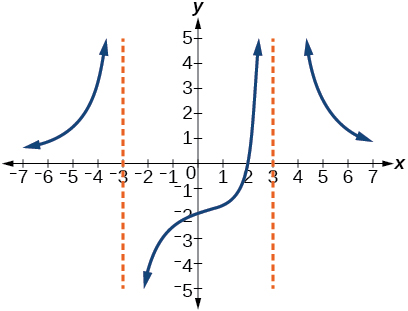
y=-9 \dfrac{x-2}{x^{2}-9}
60)
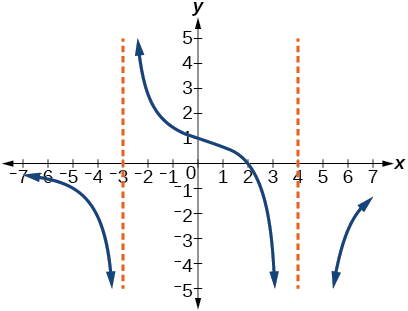
61)
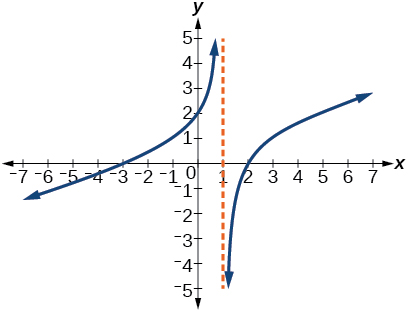
- Answer
-
y=\dfrac{1}{3} \dfrac{x^{2}+x-6}{x-1}
62)
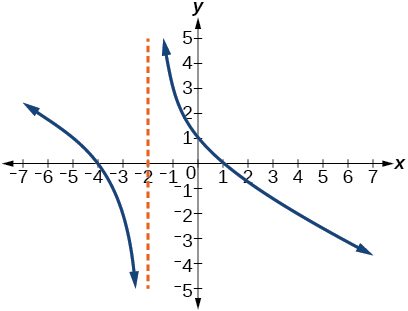
63)
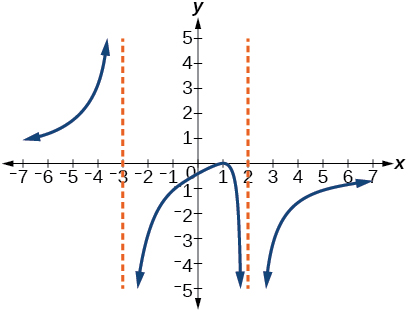
- Answer
-
y=-6 \dfrac{(x-1)^{2}}{(x+3)(x-2)^{2}}
64)
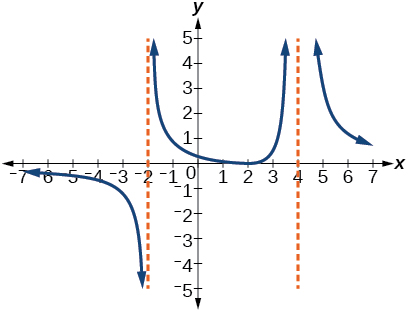
Numeric
For the exercises 65-69, make tables to show the behavior of the function near the vertical asymptote and reflecting the horizontal asymptote
65) f(x)=\dfrac{1}{x-2}
- Answer
-
x 2.01 2.001 2.0001 1.99 1.999 y 100 1,000 10,000 –100 –1,000 x 10 100 1,000 10,000 100,000 y .125 .0102 .001 .0001 .00001 Vertical asymptote x=2, Horizontal asymptote y=0
66) f(x)=\dfrac{x}{x-3}
67) f(x)=\dfrac{2x}{x+4}
- Answer
-
x –4.1 –4.01 –4.001 –3.99 –3.999 y 82 802 8,002 –798 –7998 x 10 100 1,000 10,000 100,000 y 1.4286 1.9331 1.992 1.9992 1.999992 Vertical asymptote x=-4, Horizontal asymptote y=2
68) f(x)=\dfrac{2 x}{(x-3)^{2}}
69) f(x)=\dfrac{x^{2}}{x^{2}+2 x+1}
- Answer
-
x –.9 –.99 –.999 –1.1 –1.01 y 81 9,801 998,001 121 10,201 x 10 100 1,000 10,000 100,000 y .82645 .9803 .998 .9998 Vertical asymptote x=-1
,
Technology
For the exercises 70-74, use a calculator to graph f(x). Use the graph to solve f(x)>0.
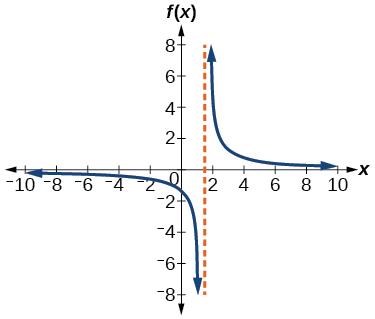
70) f(x)=\dfrac{2}{x+1}
71) f(x)=\dfrac{4}{2x-3}
- Answer
-
\left(\dfrac{3}{2}, \infty\right)
72) f(x)=\dfrac{2}{(x-1)(x+2)}
73) f(x)=\dfrac{x+2}{(x-1)(x-4)}
- Answer
-
(-2,1) \cup(4, \infty)
74) f(x)=\dfrac{(x+3)^{2}}{(x-1)^{2}(x+1)}
Extensions
For the exercises 75-79, identify the removable discontinuity.
75) f(x)=\dfrac{x^{2}-4}{x-2}
- Answer
-
(2,4)
76) f(x)=\dfrac{x^{3}+1}{x+1}
77) f(x)=\dfrac{x^{2}+x-6}{x-2}
- Answer
-
(2,5)
78) f(x)=\dfrac{2 x^{2}+5 x-3}{x+3}
79) f(x)=\dfrac{x^{3}+x^{2}}{x+1}
- Answer
-
(-1,1)
Real-World Applications
For the exercises 80-81, express a rational function that describes the situation.
80) A large mixing tank currently contains 200 gallons of water, into which 10 pounds of sugar have been mixed. A tap will open, pouring 10 gallons of water per minute into the tank at the same time sugar is poured into the tank at a rate of 3 pounds per minute. Find the concentration (pounds per gallon) of sugar in the tank after t
81) A large mixing tank currently contains 300 gallons of water, into which 8 pounds of sugar have been mixed. A tap will open, pouring 20 gallons of water per minute into the tank at the same time sugar is poured into the tank at a rate of 2 pounds per minute. Find the concentration (pounds per gallon) of sugar in the tank after t minutes.
- Answer
-
C(t)=\dfrac{8+2t}{300+20t}
For the exercises 82-83, use the given rational function to answer the question.
82) The concentration C of a drug in a patient's bloodstream t hours after injection in given by C(t)=\dfrac{2t}{3+t^{2}}. What happens to the concentration of the drug as t increases?
83) The concentration C of a drug in a patients bloodstream, hours after injection is given by C(t)=\dfrac{100t}{2 t^{2}+75}. Use a calculator to approximate the time when the concentration is highest.
- Answer
-
After about 6.12 hours.
For the exercises 84-88, construct a rational function that will help solve the problem. Then, use a calculator to answer the question.
84) An open box with a square base is to have a volume of 108 cubic inches. Find the dimensions of the box that will have minimum surface area. Let x = length of the side of the base.
85) A rectangular box with a square base is to have a volume of 20 cubic feet. The material for the base costs 30 cents/ square foot. The material for the sides costs 10 cents/square foot. The material for the top costs 20 cents/square foot. Determine the dimensions that will yield minimum cost. Let x = length of the side of the base.
- Answer
-
A(x)=50 x^{2}+\dfrac{800}{x} \cdot 2 by 2 by 5 feet.
86) A right circular cylinder has volume of 100 cubic inches. Find the radius and height that will yield minimum surface area. Let x = radius.
87) A right circular cylinder with no top has a volume of 50 cubic meters. Find the radius that will yield minimum surface area. Let x = radius.
- Answer
-
A(x)=\pi x^{2}+\dfrac{100}{x}. Radius = 2.52 meters.
88) A right circular cylinder is to have a volume of 40 cubic inches. It costs 4 cents/square inch to construct the top and bottom and 1 cent/square inch to construct the rest of the cylinder. Find the radius to yield minimum cost. Let x = radius.
3.8 Inverses and Radical Functions
Verbal
1) Explain why we cannot find inverse functions for all polynomial functions.
- Answer
-
It can be too difficult or impossible to solve for
2) Why must we restrict the domain of a quadratic function when finding its inverse?
3) When finding the inverse of a radical function, what restriction will we need to make?
- Answer
-
We will need a restriction on the domain of the answer.
4) The inverse of a quadratic function will always take what form?
Algebraic
For the exercises 5-12, find the inverse of the function on the given domain.
5) f(x)=(x-4)^{2},[4, \infty)
- Answer
-
f^{-1}(x)=\sqrt{x}+4
6) f(x)=(x+2)^{2},[-2, \infty)
7) f(x)=(x+1)^{2}-3,[-1, \infty)
- Answer
-
f^{-1}(x)=\sqrt{x+3}-1
8) f(x)=2-\sqrt{3+x}
9) f(x)=3 x^{2}+5,(-\infty, 0]
- Answer
-
f^{-1}(x)=-\sqrt{\dfrac{x-5}{3}}
10) f(x)=12-x^{2},[0, \infty)
11) f(x)=9-x^{2},[0, \infty)
- Answer
-
f(x)=\sqrt{9-x}
12) f(x)=2 x^{2}+4,[0, \infty)
For the exercises 13-16, find the inverse of the functions.
13) f(x)=x^{3}+5
- Answer
-
f^{-1}(x)=\sqrt[3]{x-5}
14) f(x)=3 x^{3}+1
15) f(x)=4-x^{3}
- Answer
-
f^{-1}(x)=\sqrt[3]{4-x}
16) f(x)=4-2 x^{3}
For the exercises 17-31, find the inverse of the functions.
17) f(x)=\sqrt{2x+1}
- Answer
-
f^{-1}(x)=\dfrac{x^{2}-1}{2},[0, \infty)
18) f(x)=\sqrt{3-4x}
19) f(x)=9+\sqrt{4x-4}
- Answer
-
f^{-1}(x)=\dfrac{(x-9)^{2}+4}{4},[9, \infty)
20) f(x)=\sqrt{6x-8}+5
21) f(x)=9+2 \sqrt[3]{x}
- Answer
-
f^{-1}(x)=\left(\dfrac{x-9}{2}\right)^{3}
22) f(x)=3-\sqrt[3]{x}
23) f(x)=\dfrac{2}{x+8}
- Answer
-
f^{-1}(x)=\dfrac{2-8x}{x}
24) f(x)=\dfrac{3}{x-4}
25) f(x)=\dfrac{x+3}{x+7}
- Answer
-
f^{-1}(x)=\dfrac{7x-3}{1-x}
26) f(x)=\dfrac{x-2}{x+7}
27) f(x)=\dfrac{3x+4}{5}
- Answer
-
f^{-1}(x)=\dfrac{5x-4}{4x+3}
28) f(x)=\dfrac{5x+1}{2-5x}
29) f(x)=x^{2}+2 x,[-1, \infty)
- Answer
-
f^{-1}(x)=\sqrt{x+1}-1
30) f(x)=x^{2}+4 x+1,[-2, \infty)
31) f(x)=x^{2}-6 x+3,[3, \infty)
- Answer
-
f^{-1}(x)=\sqrt{x+6}+3
Graphical
For the exercises 32-41, find the inverse of the function and graph both the function and its inverse.
32) f(x)=x^{2}+2, x \geq 0
33) f(x)=4-x^{2}, x \geq 0
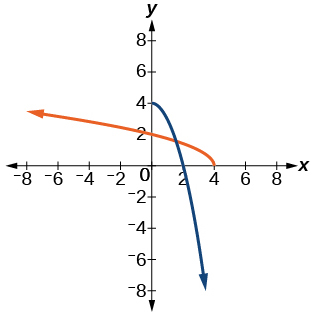
- Answer
-
f^{-1}(x)=\sqrt{4-x}
34) f(x)=(x+3)^{2}, x \geq-3
35) f(x)=(x-4)^{2}, x \geq 4
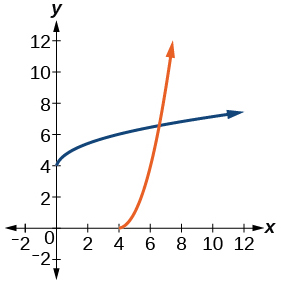
- Answer
-
f^{-1}(x)=\sqrt{x}+4
36) f(x)=x^{3}+3
37) f(x)=1-x^{3}
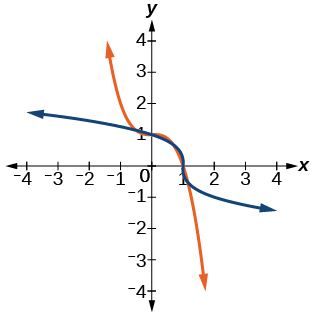
- Answer
-
f^{-1}(x)=\sqrt[3]{1-x}
38) f(x)=x^{2}+4 x, x \geq-2
39) f(x)=x^{2}-6 x+1, x \geq 3
- Answer
-
f^{-1}(x)=\sqrt{x+8}+3
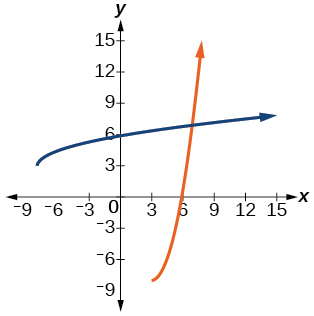
40) f(x)=\dfrac{2}{x}
41) f(x)=\dfrac{1}{x^{2}}, x \geq 0
- Answer
-
f^{-1}(x)=\sqrt{\dfrac{1}{x}}
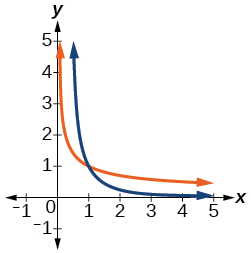
For the exercises 42-46, use a graph to help determine the domain of the functions.
42) f(x)=\sqrt{\dfrac{(x+1)(x-1)}{x}}
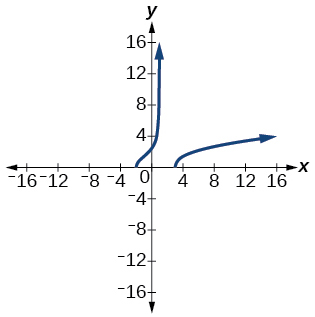
43) f(x)=\sqrt{\dfrac{(x+2)(x-3)}{x-1}}
- Answer
-
[-2,1) \cup[3, \infty)
44) f(x)=\sqrt{\dfrac{x(x+3)}{x-4}}
45) f(x)=\sqrt{\dfrac{x^{2}-x-20}{x-2}}
- Answer
-
[-4,2) \cup[5, \infty)
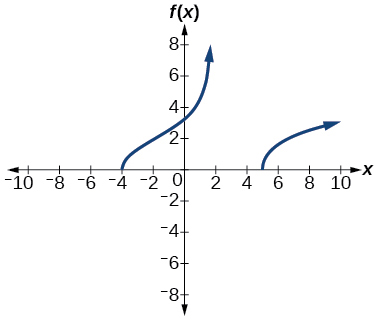
46) f(x)=\sqrt{\dfrac{9 x^{2}}{x+4}}
Technology
For the exercises 47-51, use a calculator to graph the function. Then, using the graph, give three points on the graph of the inverse with y-coordinates given.
47) f(x)=x^{3}-x-2, y=1,2,3
- Answer
-
(-2,0) ;(4,2) ;(22,3)
48) f(x)=x^{3}+x-2, y=0,1,2
49) f(x)=x^{3}+3 x-4, y=0,1,2
- Answer
-
(-4,0) ;(0,1) ;(10,2)
50) f(x)=x^{3}+8 x-4, y=-1,0,1
51) f(x)=x^{4}+5 x+1, y=-1,0,1
- Answer
-
(-3,-1) ;(1,0) ;(7,1)
Extensions
For the exercises 52-56, find the inverse of the functions with a, b, c positive real numbers.
52) f(x)=ax^{3}+b
53) f(x)=x^{2}+bx
- Answer
-
f^{-1}(x)=\sqrt{x+\dfrac{b^{2}}{4}}-\dfrac{b}{2}
54) f(x)=\sqrt{a x^{2}+b}
55) f(x)=\sqrt[3]{a x+b}
- Answer
-
f^{-1}(x)=\dfrac{x^{2}-b}{a}
56) f(x)=\dfrac{ax+b}{x+c}
Real-World Applications
For the exercises 57-66, determine the function described and then use it to answer the question.
57) An object dropped from a height of 200 meters has a height, h(t), in meters after t seconds have lapsed, such that h(t)=200-4.9 t^{2}. Express t as a function of height, h, and find the time to reach a height of 50 meters.
- Answer
-
t(h)=\sqrt{\dfrac{200-h}{4.9}}, 5.53 seconds
58) An object dropped from a height of 600 feet has a height, h(t), in feet after t seconds have elapsed, such that h(t)=600-16 t^{2}. Express t as a function of height h, and find the time to reach a height of 400 feet.
59) The volume, V, of a sphere in terms of its radius, r, is given by V(r)=\frac{4}{3} \pi r^{3}. Express r as a function of V, and find the radius of a sphere with volume of 200 cubic feet.
- Answer
-
r(V)=\sqrt[3]{\dfrac{3 V}{4 \pi}}, 3.63 feet
60) The surface area, A, of a sphere in terms of its radius, r, is given by A(r)=4 \pi r^{2}. Express r as a function of V, and find the radius of a sphere with a surface area of 1000 square inches.
61) A container holds 100 ml of a solution that is 25 ml acid. If n ml of a solution that is 60\% acid is added, the function C(n)=\dfrac{25+.6 n}{100+n} gives the concentration, C, as a function of the number of ml added, n. Express n as a function of C and determine the number of mL that need to be added to have a solution that is 50\% acid.
- Answer
-
n(C)=\dfrac{100 C-25}{6-C}, 250 \mathrm{mL}
62) The period T, in seconds, of a simple pendulum as a function of its length l, in feet, is given by T(l)=2 \pi \sqrt{\dfrac{l}{322}}. Express l as a function of T and determine the length of a pendulum with period of 2 seconds.
63) The volume of a cylinder, V, in terms of radius, r, and height, h, is given by V=\pi r^{2} h. If a cylinder has a height of 6 meters, express the radius as a function of V and find the radius of a cylinder with volume of 300 cubic meters.
- Answer
-
r(V)=\sqrt{\dfrac{V}{6 \pi}}, 3.99 meters
64) The surface area, A, of a cylinder in terms of its radius, r, and height, h, is given by A=2 \pi r^{2}+2 \pi r h. If the height of the cylinder is 4 feet, express the radius as a function of V and find the radius if the surface area is 200 square feet.
65) The volume of a right circular cone, V, in terms of its radius, r, and its height, h, is given by V=\frac{1}{3} \pi r^{2} h. Express r in terms of V if the height of the cone is 12 feet and find the radius of a cone with volume of 50 cubic inches.
- Answer
-
r(V)=\sqrt{\dfrac{V}{4 \pi}}, 1.99 inches
66) Consider a cone with height of 30 feet. Express the radius, r,
3.9 Modeling Using Variation
Verbal
1) What is true of the appearance of graphs that reflect a direct variation between two variables?
- Answer
-
The graph will have the appearance of a power function.
2) If two variables vary inversely, what will an equation representing their relationship look like?
3) Is there a limit to the number of variables that can jointly vary? Explain.
- Answer
-
No. Multiple variables may jointly vary.
Algebraic
For the exercises 4-23, write an equation describing the relationship of the given variables.
4) y varies directly as x and when x=6, y=12
5) y varies directly as the square of x and when x=4, y=80
- Answer
-
y=5 x^{2}
6) y varies directly as the square root of x and when x=36, y=24
7) y varies directly as the cube of x and when x=36, y=24
- Answer
-
y=10 x^{3}
8) y varies directly as the cube root of x and when x=27, y=15
9) y varies directly as the fourth power of x and when x=1, y=6
- Answer
-
y=6 x^{4}
10) y varies inversely as x and when x=4, y=2
11) y varies inversely as the square of x and when x=3, y=2
- Answer
-
y=\dfrac{18}{x^{2}}
12) y varies inversely as the cube of x and when x=2, y=5
13) y varies inversely as the fourth power of x and when x=3, y=1
- Answer
-
y=\dfrac{81}{x^{4}}
14) y varies inversely as the square root of x and when x=25, y=3
15) y varies inversely as the cube root of x and when x=64, y=5
- Answer
-
y=\dfrac{20}{\sqrt[3]{x}}
16) y varies jointly with x and z and when x=2 and z=3, y=36
17) y varies jointly as x, z, and w and when x=1, z=2, w=5, then y=100
- Answer
-
y=10 x z w
18) y varies jointly as the square of x and the square of z and when x=3 and z=4, then y=72
19) y varies jointly as x and the square root of z and when x=2 and z=25, then y=100
- Answer
-
y=10 x \sqrt{z}
20) y varies jointly as the square of x the cube of z and the square root of w . When x=1, z=2, and w=36, then y=48
21) y varies jointly as x and z and inversely as w. When x=3, z=5, and w=6, then y=10
- Answer
-
y=4 \dfrac{x z}{w}
22) y varies jointly as the square of x and the square root of z and inversely as the cube of w. When x=3, z=4, and w=3, then y=6
23) y varies jointly as x and z and inversely as the square root of wand the square of t. When x=3, z=1, w=25, and t=2, then y=6
- Answer
-
y=40 \dfrac{x z}{\sqrt{w} t^{2}}
Numeric
For the exercises 24-40, use the given information to find the unknown value.
24) y varies directly as x. When x=3, then y=12. Find y when x=20.
25) y varies directly as the square of x. When x=2, then y=16. Find y when x=8.
- Answer
-
y=256
26) y varies directly as the cube of x. When x=3, then y=5. Find y when x=4.
27) y varies directly as the square root of x. When x=16, then y=4. Find y when x=36.
- Answer
-
y=6
28) y varies directly as the cube root of x. When x=125, then y=15. Find y when x=1,000.
29) y varies inversely with x. When x=3, then y=2. Find y when x=1.
- Answer
-
y=6
30) y varies inversely with the square of x. When x=4, then y=3. Find y when x=2.
31) y varies inversely with the cube of x. When x=3, then y=1. Find y when x=1.
- Answer
-
y=27
32) y varies inversely with the square root of x. When x=64, then y=12. Find y when x=36.
33) y varies inversely with the cube root of x. When x=27, then y=5. Find y when x=125.
- Answer
-
y=3
34) y varies jointly as x and z. When x=4 and z=2, then y=16. Find y when x=3 and z=3.
35) y varies jointly as x, z, and w. When x=2, z=1, and w=12, then y=72. Find y when x=1, z=2, and w=3.
- Answer
-
y=18
36) y varies jointly as x and the square of z. When x=2 and z=4, then y=144. Find y when x=4 and z=5.
37) y varies jointly as the square of x and the square root of z. When x=9, then y=24. Find y when x=3 and z=25.
- Answer
-
y=90
38) y varies jointly as x and inversely as w. When x=5, z=2, and w=20, then y=4. Find y when x=3 and z=8 and w=48.
39) y varies jointly as the square of x and the cube of z and inversely as the square root of w. When x=2, z=2, and w=64 then y=12. Find y when x=1, z=3, and w=4.
- Answer
-
y=\dfrac{81}{2}
40) y varies jointly as the square of x and of z and inversely as the square root of wand of t. When x=2, z=3, w=16, and t=3, then y=1. Find y when x=3, z=2, w=36, and t=5.
Technology
For the exercises 41-45, use a calculator to graph the equation implied by the given variation.
41) y varies directly with the square of x and when x=2, y=3
- Answer
-
y=\dfrac{3}{4} x^{2}
42) y varies directly as the cube of x and when x=2, y=4.
43) y varies directly as the square root of x and when x=36, y=2.
- Answer
-
y=\dfrac{1}{3} \sqrt{x}
44) y varies inversely with x and when x=6, y=2.
45) y varies inversely as the square of x and when x=1, y=4.
- Answer
-
y=\dfrac{4}{x^{2}}
Extensions
For the exercises 46-50, use Kepler’s Law, which states that the square of the time, T, required for a planet to orbit the Sun varies directly with the cube of the mean distance, a, that the planet is from the Sun.
46) Using the Earth’s time of 1 year and mean distance of 93 million miles, find the equation relating T and a.
47) Use the result from the previous exercise to determine the time required for Mars to orbit the Sun if its mean distance is 142 million miles.
- Answer
-
1.89 years
48) Using Earth’s distance of 150 million kilometers, find the equation relating T and a.
49) Use the result from the previous exercise to determine the time required for Venus to orbit the Sun if its mean distance is 108 million kilometers.
- Answer
-
0.61 years
50) Using Earth’s distance of 1 astronomical unit (A.U.), determine the time for Saturn to orbit the Sun if its mean distance is 9.54 A.U.
Real-World Applications
For the exercises 51-60, use the given information to answer the questions.
51) The distance s that an object falls varies directly with the square of the time, t, of the fall. If an object falls 16 feet in one second, how long for it to fall 144 feet?
- Answer
-
3 seconds
52) The velocity v of a falling object varies directly to the time, t, of the fall. If after 2 seconds, the velocity of the object is 64 feet per second, what is the velocity after 5 seconds?
53) The rate of vibration of a string under constant tension varies inversely with the length of the string. If a string is 24 inches long and vibrates 128 times per second, what is the length of a string that vibrates 64 times per second?
- Answer
-
48 inches
54) The volume of a gas held at constant temperature varies indirectly as the pressure of the gas. If the volume of a gas is 1200 cubic centimeters when the pressure is 200 millimeters of mercury, what is the volume when the pressure is 300 millimeters of mercury?
55) The weight of an object above the surface of the Earth varies inversely with the square of the distance from the center of the Earth. If a body weighs 50 pounds when it is 3960 miles from Earth’s center, what would it weigh it were 3970 miles from Earth’s center?
- Answer
-
49.75 pounds
56) The intensity of light measured in foot-candles varies inversely with the square of the distance from the light source. Suppose the intensity of a light bulb is 0.08 foot-candles at a distance of 3 meters. Find the intensity level at 8 meters.
57) The current in a circuit varies inversely with its resistance measured in ohms. When the current in a circuit is 40 amperes, the resistance is 10 ohms. Find the current if the resistance is 12 ohms.
- Answer
-
33.33 amperes
58) The force exerted by the wind on a plane surface varies jointly with the square of the velocity of the wind and with the area of the plane surface. If the area of the surface is 40 square feet surface and the wind velocity is 20 miles per hour, the resulting force is 15 pounds. Find the force on a surface of 65 square feet with a velocity of 30 miles per hour.
59) The horsepower (hp) that a shaft can safely transmit varies jointly with its speed (in revolutions per minute (rpm)) and the cube of the diameter. If the shaft of a certain material 3 inches in diameter can transmit 45 hp at 100 rpm, what must the diameter be in order to transmit 60 hp at 150 rpm?
- Answer
-
2.88 inches
60) The kinetic energy K of a moving object varies jointly with its mass m and the square of its velocity v. If an object weighing 40 kilograms with a velocity of 15 meters per second has a kinetic energy of 1000 joules, find the kinetic energy if the velocity is increased to 20 meters per second.


