3.R: Polynomial and Rational Functions(Review)
- Page ID
- 19674
3.1 Complex Numbers
Perform the indicated operation with complex numbers.
1) \((4+3 i)+(-2-5 i)\)
- Answer
-
\(2-2 i\)
2) \((6-5 i)-(10+3 i)\)
3) \((2-3 i)(3+6 i)\)
- Answer
-
\(24+3 i\)
4) \(\dfrac{2-i}{2+i}\)
Solve the following equations over the complex number system.
5) \(x^{2}-4 x+5=0\)
- Answer
-
\(\{2+i, 2-i\}\)
6) \(x^{2}+2 x+10=0\)
3.2 Quadratic Functions
For the exercises 1-2, write the quadratic function in standard form. Then, give the vertex and axes intercepts. Finally, graph the function.
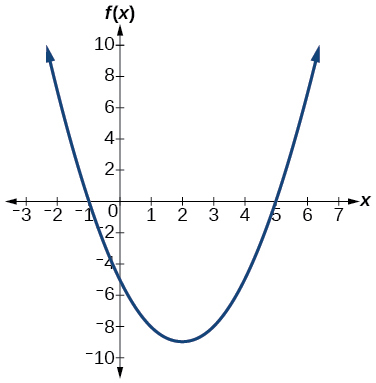
1) \(f(x)=x^{2}-4 x-5\)
- Answer
-
\(f(x)=(x-2)^{2}-9\) vertex \((2,-9)\), intercepts \((5,0); (-1,0); (0,-5)\)
2) \(f(x)=-2 x^{2}-4 x\)
For the problems 3-4, find the equation of the quadratic function using the given information.
3) The vertex is \((-2,3)\) and a point on the graph is \((3,6)\).
- Answer
-
\(f(x)=\dfrac{3}{25}(x+2)^{2}+3\)
4) The vertex is \((-3,6.5)\) and a point on the graph is \((2,6)\).
Answer the following questions.
5) A rectangular plot of land is to be enclosed by fencing. One side is along a river and so needs no fence. If the total fencing available is \(600\) meters, find the dimensions of the plot to have maximum area.
- Answer
-
\(300\) meters by \(150\) meters, the longer side parallel to river.
6) An object projected from the ground at a \(45\) degree angle with initial velocity of \(120\) feet per second has height, \(h\), in terms of horizontal distance traveled, \(x\),
3.3 Power Functions and Polynomial Functions
For the exercises 1-3, determine if the function is a polynomial function and, if so, give the degree and leading coefficient.
1) \(f(x)=4 x^{5}-3 x^{3}+2 x-1\)
- Answer
-
Yes, \(\text{degree} = 5\), \(\text{leading coefficient} = 4\)
2) \(f(x)=5^{x+1}-x^{2}\)
3) \(f(x)=x^{2}\left(3-6 x+x^{2}\right)\)
- Answer
-
Yes, \(\text{degree} = 4\), \(\text{leading coefficient} = 1\)
For the exercises 4-6, determine end behavior of the polynomial function.
4) \(f(x)=2 x^{4}+3 x^{3}-5 x^{2}+7\)
5) \(f(x)=4 x^{3}-6 x^{2}+2\)
- Answer
-
As \(x \rightarrow-\infty, f(x) \rightarrow-\infty \), as \(x \rightarrow \infty, f(x) \rightarrow \infty\)
6) \(f(x)=2 x^{2}\left(1+3 x-x^{2}\right)\)
3.4 Graphs of Polynomial Functions
For the exercises 1-3, find all zeros of the polynomial function, noting multiplicities.
1) \(f(x)=(x+3)^{2}(2 x-1)(x+1)^{3}\)
- Answer
-
\(-3\) with multiplicity \(2\), \(-\dfrac{1}{2}\) with multiplicity \(1\), \(-1\) with multiplicity \(3\)
2) \(f(x)=x^{5}+4 x^{4}+4 x^{3}\)
3) \(f(x)=x^{3}-4 x^{2}+x-4\)
- Answer
-
\(4\) with multiplicity \(1\)
For the exercises 4-5, based on the given graph, determine the zeros of the function and note multiplicity.
4)
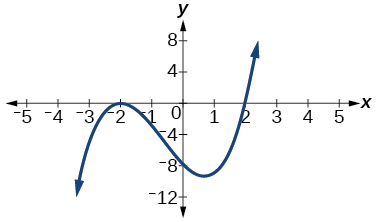
5)
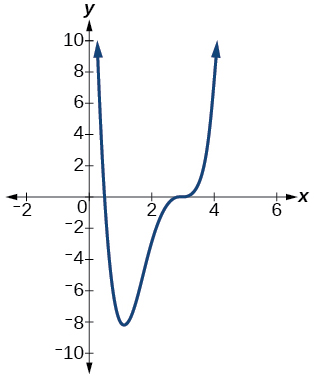
- Answer
-
\(\dfrac{1}{2}\) with multiplicity \(1\), \(3\) with multiplicity \(3\)
6) Use the Intermediate Value Theorem to show that at least one zero lies between \(2\) and \(3\) for the function \(f(x)=x^{3}-5 x+1\)
3.5 Dividing Polynomials
For the exercises 1-2, use long division to find the quotient and remainder.
1) \(\dfrac{x^{3}-2 x^{2}+4 x+4}{x-2}\)
- Answer
-
\(x^{2}+4\) with remainder \(12\)
2) \(\dfrac{3 x^{4}-4 x^{2}+4 x+8}{x+1}\)
For the exercises 3-6, use synthetic division to find the quotient. If the divisor is a factor, then write the factored form.
3) \(\dfrac{x^{2}-2 x^{2}+5 x-1}{x+3}\)
- Answer
-
\(x^{2}-5 x+20-\dfrac{61}{x+3}\)
4) \(\dfrac{x^{2}+4 x+10}{x-3}\)
5) \(\dfrac{2 x^{3}+6 x^{2}-11 x-12}{x+4}\)
- Answer
-
\(2 x^{2}-2x-3\), so factored form is \((x+4)\left(2 x^{2}-2x-3\right)\)
6) \(\dfrac{3 x^{4}+3 x^{3}+2 x+2}{x+1}\)
3.6 Zeros of Polynomial Functions
For the exercises 1-4, use the Rational Zero Theorem to help you solve the polynomial equation.
1) \(2 x^{3}-3 x^{2}-18 x-8=0\)
- Answer
-
\(\left\{-2,4,-\dfrac{1}{2}\right\}\)
2) \(3x^{3}+11 x^{2}+8 x-4=0\)
3) \(2 x^{4}-17 x^{3}+46 x^{2}-43 x+12=0\)
- Answer
-
\(\left\{1,3,4, \dfrac{1}{2}\right\}\)
4) \(4 x^{4}+8 x^{3}+19 x^{2}+32 x+12=0\)
For the exercises 5-6, use Descartes’ Rule of Signs to find the possible number of positive and negative solutions.
5) \(x^{3}-3 x^{2}-2 x+4=0\)
- Answer
-
\(0\) or \(2\) positive, \(1\) negative
6) \(2 x^{4}-x^{3}+4 x^{2}-5 x+1=0\)
3.7 Rational Functions
For the following rational functions 1-4, find the intercepts and the vertical and horizontal asymptotes, and then use them to sketch a graph.
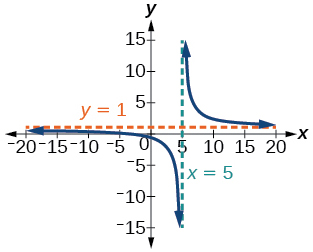
1) \(f(x)=\dfrac{x+2}{x-5}\)
- Answer
-
Intercepts \((-2,0)\) and \(\left(0,-\dfrac{2}{5}\right)\), Asymptotes \(x=5\) and \(y=1\)
2) \(f(x)=\dfrac{x^{2}+1}{x^{2}-4}\)
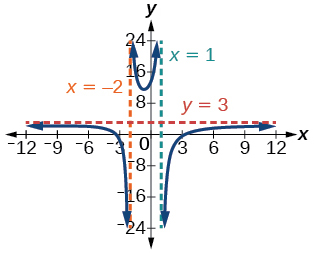
3) \(f(x)=\dfrac{3 x^{2}-27}{x^{2}-9}\)
- Answer
-
Intercepts \((3,0),(-3,0)\), and \(\left(0, \dfrac{27}{2}\right)\), Asymptotes \(x=1, x=-2, y=3\)
4) \(f(x)=\dfrac{x+2}{x^{2}-9}\)
For the exercises 5-6, find the slant asymptote.
5) \(f(x)=\dfrac{x^{2}-1}{x+2}\)
- Answer
-
\(y=x-2\)
6) \(f(x)=\dfrac{2 x^{3}-x^{2}+4}{x^{2}+1}\)
3.8 Inverses and Radical Functions
For the exercises 1-6, find the inverse of the function with the domain given.
1) \(f(x)=(x-2)^{2}, x \geq 2\)
- Answer
-
\(f^{-1}(x)=\sqrt{x}+2\)
2) \(f(x)=(x+4)^{2}-3, x \geq-4\)
3) \(f(x)=x^{2}+6 x-2, x \geq-3\)
- Answer
-
\(f^{-1}(x)=\sqrt{x+11}-3\)
4) \(f(x)=2 x^{3}-3\)
5) \(f(x)=\sqrt{4 x+5}-3\)
- Answer
-
\(f^{-1}(x)=\dfrac{(x+3)^{2}-5}{4}, x \geq-3\)
6) \(f(x)=\dfrac{x-3}{2 x+1}\)
3.9 Modeling Using Variation
For the exercises 1-4, find the unknown value.
1) \(y\) varies directly as the square of \(x\). If when \(x=3, y=36\), find \(y\) if \(x=4\).
- Answer
-
\(y=64\)
2) \(y\) varies inversely as the square root of \(x\). If when \(x=25, y=2\), find \(y\) if \(x=4\).
3) \(y\) varies jointly as the cube of \(x\) and as \(z\). If when \(x=1\) and \(z=2, y=6\), find \(y\) if \(x=2\) and \(z=3\).
- Answer
-
\(y=72\)
4) \(y\) varies jointly as \(x\) and the square of \(z\) and inversely as the cube of \(w\). If when \(x=3, z=4\), and \(w=2, y=48\), ind \(y\) if \(x=4, z=5\), and \(w=3\).
For the exercises 5-6, solve the application problem.
5) The weight of an object above the surface of the earth varies inversely with the distance from the center of the earth. If a person weighs \(150\) pounds when he is on the surface of the earth (\(3,960\) miles from center), find the weight of the person if he is \(20\) miles above the surface.
- Answer
-
\(148.5\) pounds
6) The volume \(V\) of an ideal gas varies directly with the temperature \(T\) and inversely with the pressure\(P\). A cylinder contains oxygen at a temperature of \(310\) degrees K and a pressure of \(18\) atmospheres in a volume of \(120\) liters. Find the pressure if the volume is decreased to \(100\) liters and the temperature is increased to \(320\) degrees K.
Practice Test
Perform the indicated operation or solve the equation.
1) \((3-4 i)(4+2 i)\)
- Answer
-
\(20-10 i\)
2) \(\dfrac{1-4 i}{3+4 i}\)
3) \(x^{2}-4 x+13=0\)
- Answer
-
\(\{2+3 i, 2-3 i\}\)
4) Give the degree and leading coefficient of the following polynomial function. \[f(x)=x^{3}\left(3-6 x^{2}-2 x^{2}\right) \nonumber \]
Determine the end behavior of the polynomial function.
5) \(f(x)=8 x^{3}-3 x^{2}+2 x-4\)
- Answer
-
As \(x \rightarrow-\infty, f(x) \rightarrow-\infty\), as \(x \rightarrow \infty, f(x) \rightarrow \infty\)
6) \(f(x)=-2 x^{2}\left(4-3 x-5 x^{2}\right)\)
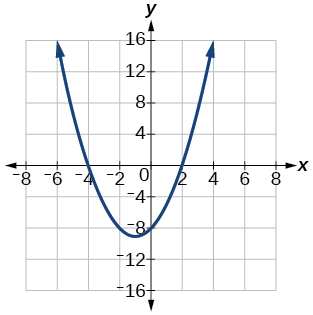
7) Write the quadratic function in standard form. Determine the vertex and axes intercepts and graph the function. \[f(x)=x^{2}+2 x-8 \nonumber \]
- Answer
-
\(f(x)=(x+1)^{2}-9,\) vertex \((-1,-9),\) intercepts \((2,0); (-4,0); (0,-8)\)
8) Given information about the graph of a quadratic function, find its equation: Vertex \((2,0)\) and point on graph \((4,12)\)
Solve the following application problem.
9) A rectangular field is to be enclosed by fencing. In addition to the enclosing fence, another fence is to divide the field into two parts, running parallel to two sides. If \(1,200\) feet of fencing is available, find the maximum area that can be enclosed.
- Answer
-
\(60,000\) square feet
Find all zeros of the following polynomial functions, noting multiplicities.
10) \(f(x)=(x-3)^{3}(3 x-1)(x-1)^{2}\)
11) \(f(x)=2 x^{6}-12 x^{5}+18 x^{4}\)
- Answer
-
\(0\) with multiplicity \(4\), \(3\) with multiplicity \(2\)
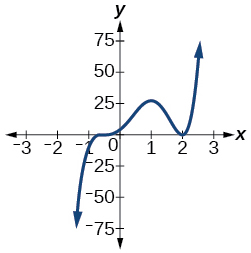
12) Based on the graph, determine the zeros of the function and multiplicities.
13) Use long division to find the quotient: \[\dfrac{2 x^{2}+3 x-4}{x+2} \nonumber \]
- Answer
-
\(2 x^{2}-4 x+11-\dfrac{26}{x+2}\)
Use synthetic division to find the quotient. If the divisor is a factor, write the factored form.
14) \(\dfrac{x^{4}+3 x^{2}-4}{x-2}\)
15) \(\dfrac{2 x^{3}+5 x^{2}-7 x-12}{x+3}\)
- Answer
-
\(2 x^{2}-x-4\). So factored form is \((x+3)\left(2 x^{2}-x-4\right)\)
Use the Rational Zero Theorem to help you find the zeros of the polynomial functions.
16) \(f(x)=2 x^{3}+5 x^{2}-6 x-9\)
17) \(f(x)=4 x^{4}+8 x^{3}+21 x^{2}+17 x+4\)
- Answer
-
\(-\dfrac{1}{2}\) (has multiplicity \(2\)), \(\dfrac{-1+i \sqrt{15}}{2}\)
18) \(f(x)=4 x^{4}+16 x^{3}+13 x^{2}-15 x-18\)
19) \(f(x)=x^{5}+6 x^{4}+13 x^{3}+14 x^{2}+12 x+8\)
- Answer
-
\(-2\) (has multiplicity \(3\)), \(\pm i\)
Given the following information about a polynomial function, find the function.
20) It has a double zero at \(x=3\) and zeroes at \(x=1\) and \(x=-2\). Its \(y\) -intercept is \((0,12)\).
21) It has a zero of multiplicity \(3\) at \(x=\dfrac{1}{2}\) and another zero at \(x=-3\). It contains the point \((1,8)\).
- Answer
-
\(f(x)=2(2 x-1)^{3}(x+3)\)
22) Use Descartes’ Rule of Signs to determine the possible number of positive and negative solutions. \[8 x^{3}-21 x^{2}+6=0 \nonumber \]
For the following rational functions, find the intercepts and horizontal and vertical asymptotes, and sketch a graph.
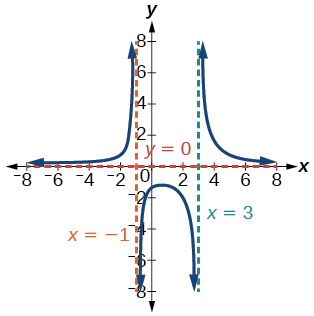
23) \(f(x)=\dfrac{x+4}{x^{2}-2 x-3}\)
- Answer
-
Intercepts \((-4,0)\), \(\left(0,-\dfrac{4}{3}\right)\), Asymptotes \(x=3, x=-1, y=0\)
24) \(f(x)=\dfrac{x^{2}+2 x-3}{x^{2}-4}\)
25) Find the slant asymptote of the rational function. \[f(x)=\dfrac{x^{2}+3 x-3}{x-1} \nonumber \]
- Answer
-
\(y=x+4\)
Find the inverse of the function.
26) \(f(x)=\sqrt{x-2}+4\)
27) \(f(x)=3 x^{3}-4\)
- Answer
-
\(f^{-1}(x)=\sqrt[3]{\dfrac{x+4}{3}}\)
28) \(f(x)=\dfrac{2 x+3}{3 x-1}\)
Find the unknown value.
29) \(y\) varies inversely as the square of \(x\) and when \(x=3, y=2\). Find \(y\) if \(x=1\).
- Answer
-
\(y=18\)
30) \(y\) varies jointly with \(x\) and the cube root of \(z\). If when \(x=27, y=12\), find \(y\) if \(x=5\) and \(z=8\).
Solve the following application problem.
31) The distance a body falls varies directly as the square of the time it falls. If an object falls \(64\) feet in \(2\) seconds, how long will it take to fall \(256\) feet?
- Answer
-
\(4\) seconds


