10.R: Analytic Geometry (Review)
- Page ID
- 18838
10.1: The Ellipse
In this section, we will investigate the shape of this room and its real-world applications, including how far apart two people in Statuary Hall can stand and still hear each other whisper.
For the exercises 1-4, write the equation of the ellipse in standard form. Then identify the center, vertices, and foci.
1) \(\dfrac{x^2}{25}+\dfrac{y^2}{64}=1\)
- Answer
-
\(\dfrac{x^2}{5^2}+\dfrac{y^2}{8^2}=1\); center: \((0,0)\); Vertices: \((5,0)\), \((-5,0)\), \((0,8)\), \((0,-8)\); foci: \((0,\sqrt{39})\), \((0,-\sqrt{39})\)
2) \(\dfrac{(x-2)^2}{100}+\dfrac{(y+3)^2}{36}=1\)
3) \(9x^2+y^2+54x-4y+76=0\)
- Answer
-
\(\dfrac{(x+3)^2}{1^2}+\dfrac{(y-2)^2}{3^2}=1\); center: \((-3,2)\); Vertices: \((-2,2)\), \((-4,2)\), \((-3,5)\), \((-3,-1)\); foci: \((-3,2+2\sqrt{2})\), \((-3,2-2\sqrt{2})\)
4) \(9x^2+36y^2-36x+72y+36=0\)
For the exercises 5-8, graph the ellipse, noting center, vertices, and foci.
5) \(\dfrac{x^2}{36}+\dfrac{y^2}{9}=1\)
- Answer
-
center: \((0,0)\); Vertices: \((6,0\), \((-6,0)\), \((0,3)\), \((0,-3)\); foci: \((3\sqrt{3},0)\), \((-3\sqrt{3},0)\)
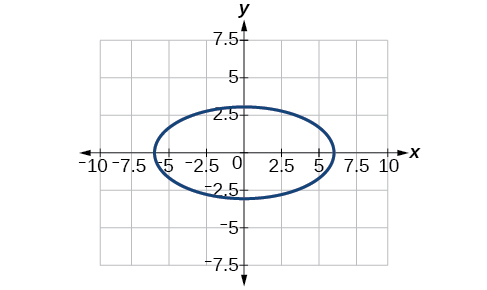
6) \(\dfrac{(x-4)^2}{25}+\dfrac{(y+3)^2}{49}=1\)
7) \(4x^2+y^2+16x+4y-44=0\)
- Answer
-
center: \((-2,-2)\); Vertices: \((2,-2)\), \((-6,-2)\), \((-2,6)\), \((-2,-10)\); foci: \((-2,-2+4\sqrt{3})\), \((-2,-2-4\sqrt{3})\)
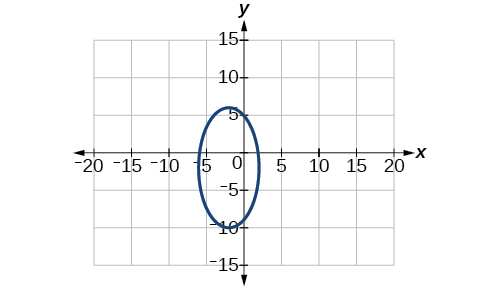
8) \(2x^2+3y^2-20x+12y+38=0\)
For the exercises 9-11, use the given information to find the equation for the ellipse.
9) Center at \((0,0)\), focus at \((3,0)\), vertex at \((-5,0)\)
- Answer
-
\(\dfrac{x^2}{25}+\dfrac{y^2}{16}=1\)
10) Center at \((2,-2)\), vertex at \((7,-2)\), focus at \((4,-2)\)
11) A whispering gallery is to be constructed such that the foci are located \(35\) feet from the center. If the length of the gallery is to be \(100\) feet, what should the height of the ceiling be?
- Answer
-
Approximately \(35.71\) feet
10.2: The Hyperbola
In analytic geometry, a hyperbola is a conic section formed by intersecting a right circular cone with a plane at an angle such that both halves of the cone are intersected. This intersection produces two separate unbounded curves that are mirror images of each other.
For the exercises 1-4, write the equation of the hyperbola in standard form. Then give the center, vertices, and foci.
1) \(\dfrac{x^2}{81}-\dfrac{y^2}{9}=1\)
2) \(\dfrac{(y+1)^2}{16}-\dfrac{(x-4)^2}{36}=1\)
- Answer
-
\(\dfrac{(y+1)^2}{4^2}-\dfrac{(x-4)^2}{6^2}=1\); center: \((4,-1)\); Vertices: \((4,3)\), \((4,-5)\); foci: \((4,-1+2\sqrt{13})\), \((4,-1-2\sqrt{13})\)
3) \(9y^2-4x^2+54y-16x+29=0\)
4) \(3x^2-y^2-12x-6y-9=0\)
- Answer
-
\(\dfrac{(x-2)^2}{2^2}-\dfrac{(y+3)^2}{(2\sqrt{3})^2}=1\); center: \((2,-3)\); Vertices: \((4,-3)\), \((0,-3)\); foci: \((6,-3)\), \((-2,-3)\)
For the exercises 5-8, graph the hyperbola, labeling vertices and foci.
5) \(\dfrac{x^2}{9}-\dfrac{y^2}{16}=1\)
6) \(\dfrac{(y-1)^2}{49}-\dfrac{(x+1)^2}{4}=1\)
- Answer
-
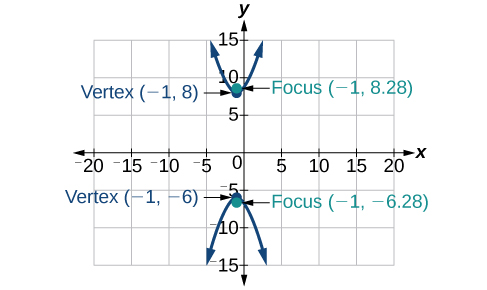
7) \(x^2-4y^2+6x+32y-91=0\)
8) \(2y^2-x^2-12y-6=0\)
- Answer
-
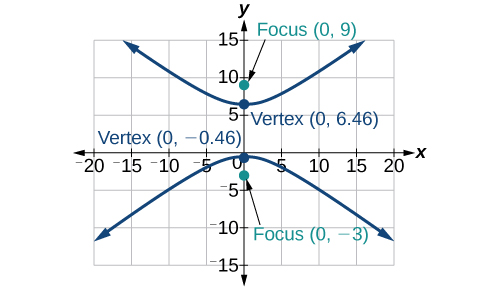
For the exercises 9-10, find the equation of the hyperbola.
9) Center at \((0,0)\), vertex at \((0,4)\), focus at \((0,-6)\)
10) Foci at \((3,7)\) and \((7,7)\), vertex at \((6,7\)
- Answer
-
\(\dfrac{(x-5)^2}{1}-\dfrac{(y-7)^2}{3}=1\)
10.3: The Parabola
Like the ellipse and hyperbola, the parabola can also be defined by a set of points in the coordinate plane. A parabola is the set of all points in a plane that are the same distance from a fixed line, called the directrix, and a fixed point (the focus) not on the directrix.
For the exercises 1-4, write the equation of the parabola in standard form. Then give the vertex, focus, and directrix.
1) \(y^2=12x\)
2) \((x+2)^2=\dfrac{1}{2}(y-1)\)
- Answer
-
\((x+2)^2=\dfrac{1}{2}(y-1)\); vertex: \((-2,1)\); focus: \( \left( -2, \dfrac{9}{8} \right ) \); directrix: \(y=\dfrac{7}{8}\)
3) \(y^2-6y-6x-3=0\)
4) \(x^2+10x-y+23=0\)
- Answer
-
\((x+5)^2=(y+2)\); vertex: \((-5,-2)\); focus: \( \left( -5, -\dfrac{7}{4} \right ) \); directrix: \(y=-\dfrac{9}{4}\)
For the exercises 5-8, graph the parabola, labeling vertex, focus, and directrix.
5) \(x^2+4y=0\)
6) \((y-1)^2=\dfrac{1}{2}(x+3)\)
- Answer
-
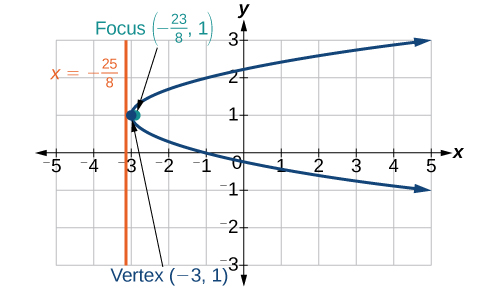
7) \(x^2-8x-10y+46=0\)
8) \(2y^2+12y+6x+15=0\)
- Answer
-
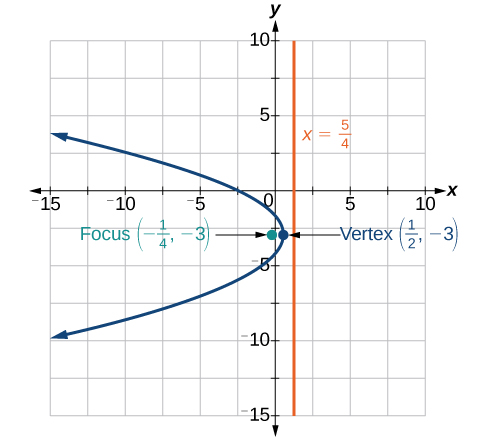
For the exercises 9-11, write the equation of the parabola using the given information.
9) Focus at \((-4,0)\); directrix is \(x=4\)
10) Focus at \( \left( 2, \dfrac{9}{8} \right ) \); directrix is \(y=\dfrac{7}{8}\)
- Answer
-
\((x-2)^2= \left (\dfrac{1}{2} \right ) (y-1)\)
11) A cable TV receiving dish is the shape of a paraboloid of revolution. Find the location of the receiver, which is placed at the focus, if the dish is \(5\) feet across at its opening and \(1.5\) feet deep.
10.4: Rotation of Axes
In previous sections of this chapter, we have focused on the standard form equations for nondegenerate conic sections. In this section, we will shift our focus to the general form equation, which can be used for any conic. The general form is set equal to zero, and the terms and coefficients are given in a particular order, as shown below.
For the exercises 1-3, determine which of the conic sections is represented.
1) \(16x^2+24xy+9y^2+24x-60y-60=0\)
- Answer
-
\(B^2 - 4AC =0\), parabola
2) \(4x^2+14xy+5y^2+18x-6y+30=0\)
3) \(4x^2+xy+2y^2+8x-26y+9=0\)
- Answer
-
\(B^2 - 4AC = -31 < 0\), ellipse
For the exercises 4-5, determine the angle \(\theta \) that will eliminate the \(xy\) term, and write the corresponding equation without the \(xy\) term.
4) \(x^2+4xy-2y^2-6=0\)
5) \(x^2-xy+y^2-6=0\)
- Answer
-
\(\theta =45^{\circ},x'^2+3y'^2-12=0\)
For the exercises 6-8, graph the equation relative to the \(x'y'\) system in which the equation has no \(x'y'\) term.
6) \(9x^2-24xy+16y^2-80x-60y+100=0\)
7) \(x^2-xy+y^2-2=0\)
- Answer
-
\(\theta =45^{\circ}\)
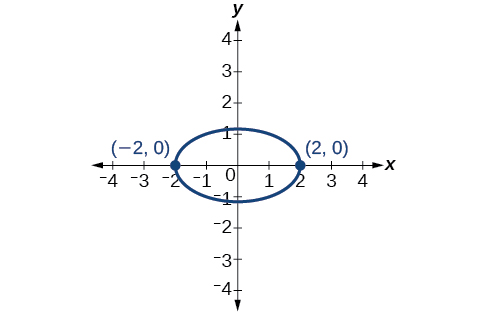
8) \(6x^2+24xy-y^2-12x+26y+11=0\)
10.5: Conic Sections in Polar Coordinates
In this section, we will learn how to define any conic in the polar coordinate system in terms of a fixed point, the focus at the pole, and a line, the directrix, which is perpendicular to the polar axis.
For the exercises 1-4, given the polar equation of the conic with focus at the origin, identify the eccentricity and directrix.
1) \(r=\dfrac{10}{1-5\cos \theta }\)
- Answer
-
Hyperbola with \(e=5\) and directrix \(2\) units to the left of the pole.
2) \(r=\dfrac{6}{3+2\cos \theta }\)
3) \(r=\dfrac{1}{4+3\sin \theta }\)
- Answer
-
Ellipse with \(e=\dfrac{3}{4}\) and directrix \(\dfrac{1}{3}\) unit above the pole.
4) \(r=\dfrac{3}{5-5\sin \theta }\)
For the exercises 5-8, graph the conic given in polar form. If it is a parabola, label the vertex, focus, and directrix. If it is an ellipse or a hyperbola, label the vertices and foci.
5) \(r=\dfrac{3}{1-\sin \theta }\)
- Answer
-
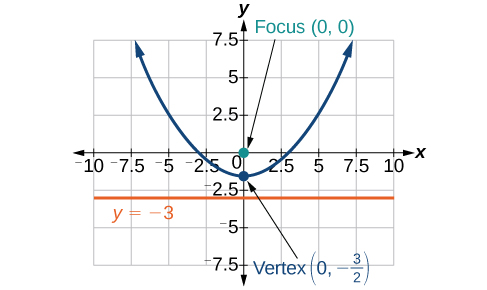
6) \(r=\dfrac{8}{4+3\sin \theta }\)
7) \(r=\dfrac{10}{4+5\cos \theta }\)
- Answer
-
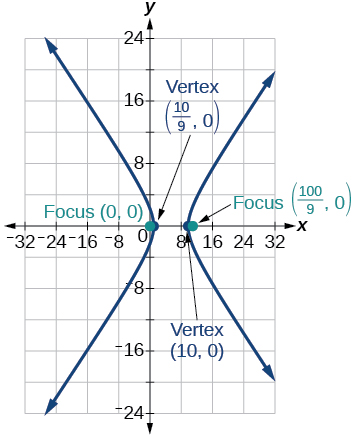
8) \(r=\dfrac{9}{3-6\cos \theta }\)
For the exercises 9-10, given information about the graph of a conic with focus at the origin, find the equation in polar form.
9) Directrix is \(x=3\) and eccentricity \(e=1\)
- Answer
-
\(r=\dfrac{3}{1+\cos \theta }\)
10) Directrix is \(y=-2\) and eccentricity \(e=4\)
Practice Test
For the exercises 1-2, write the equation in standard form and state the center, vertices, and foci.
1) \(\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\)
- Answer
-
\(\dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}=1\); center: \((0,0)\); vertices: \((3,0)\), \((-3,0)\), \((0,2)\), \((0,-2)\); foci: \((\sqrt{5},0)\), \((-\sqrt{5},0)\)
2) \(9y^2+16x^2-36y+32x-92=0\)
For the exercises 3-6, sketch the graph, identifying the center, vertices, and foci.
3) \(\dfrac{(x-3)^2}{64}+\dfrac{(y-2)^2}{36}=1\)
- Answer
-
center: \((3,2)\); vertices: \((11,2)\), \((-5,2)\), \((3,8)\), \((3,-4)\); foci: \((3+2\sqrt{7},2)\), \((3-2\sqrt{7},2)\)
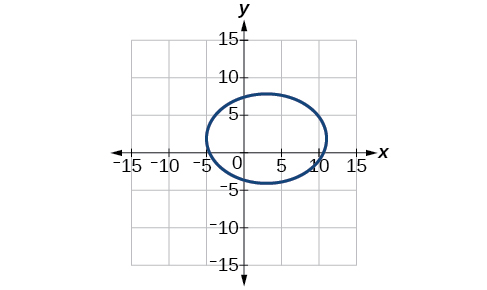
4) \(2x^2+y^2+8x-6y-7=0\)
5) Write the standard form equation of an ellipse with a center at \((1,2)\), vertex at \((7,2)\), and focus at \((4,2)\).
- Answer
-
\(\dfrac{(x-1)^2}{36}+\dfrac{(y-2)^2}{27}=1\)
6) A whispering gallery is to be constructed with a length of \(150\) feet. If the foci are to be located \(20\) feet away from the wall, how high should the ceiling be?
For the exercises 7-8, write the equation of the hyperbola in standard form, and give the center, vertices, foci, and asymptotes.
7) \(\dfrac{x^2}{49}-\dfrac{y^2}{81}=1\)
- Answer
-
\(\dfrac{x^2}{7^2}-\dfrac{y^2}{9^2}=1\); center: \((0,0)\); vertices: \((7,0)\), \((-7,0)\); foci: \((\sqrt{130},0)\), \((-\sqrt{130},0)\); asymptotes: \(y=\pm \dfrac{9}{7}x\)
8) \(16y^2-9x^2+128y+112=0\)
For the exercises 9-11, graph the hyperbola, noting its center, vertices, and foci. State the equations of the asymptotes.
9) \(\dfrac{(x-3)^2}{25}-\dfrac{(y+3)^2}{1}=1\)
- Answer
-
center: \((3,-3)\); vertices: \((8,-3)\), \((-2,-3)\); foci: \((3+\sqrt{26},-3)\), \((3-\sqrt{26},-3)\); asymptotes: \(y=\pm \dfrac{1}{5}(x-3)-3\)
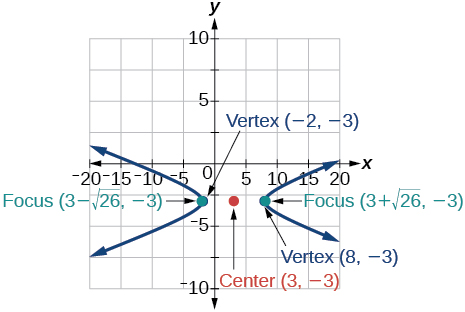
10) \(y^2-x^2+4y-4x-18=0\)
11) Write the standard form equation of a hyperbola with foci at \((1,0)\), and \((1,6)\), and a vertex at \((1,2)\).
- Answer
-
\(\dfrac{(y-3)^2}{1}-\dfrac{(x-1)^2}{8}=1\)
For the exercises 12-13, write the equation of the parabola in standard form, and give the vertex, focus, and equation of the directrix.
12) \(y^2+10x=0\)
13) \(3x^2-12x-y+11=0\)
- Answer
-
\((x-2)^2=\dfrac{1}{3}(y+1)\); vertex: \((2,-1)\); focus: \((2,-\dfrac{11}{12})\); directrix: \(y=-\dfrac{13}{12}\)
For the exercises 14-17, graph the parabola, labeling the vertex, focus, and directrix.
14) \((x-1)^2=-4(y+3)\)
15) \(y^2+8x-8y+40=0\)
- Answer
-
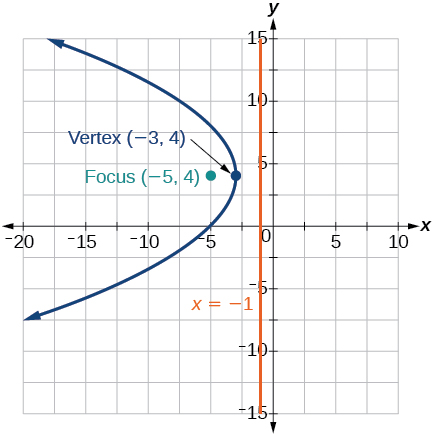
16) Write the equation of a parabola with a focus at \((2,3)\) and directrix \(y=-1\).
17) A searchlight is shaped like a paraboloid of revolution. If the light source is located \(1.5\) feet from the base along the axis of symmetry, and the depth of the searchlight is \(3\) feet, what should the width of the opening be?
- Answer
-
Approximately \(8.49\) feet
For the exercises 18-19, determine which conic section is represented by the given equation, and then determine the angle \(\theta\) that will eliminate the \(xy\) term.
18) \(3x^2-2xy+3y^2=4\)
19) \(x^2+4xy+4y^2+6x-8y=0\)
- Answer
-
parabola; \(\theta \approx 63.4^{\circ}\)
For the exercises 20-21, rewrite in the \(x'y'\) system without the \(x'y'\) term, and graph the rotated graph.
20) \(11x^2+10\sqrt{3}xy+y^2=4\)
21) \(16x^2+24xy+9y^2-125x=0\)
- Answer
-
\(x'^2-4x'+3y'=0\)
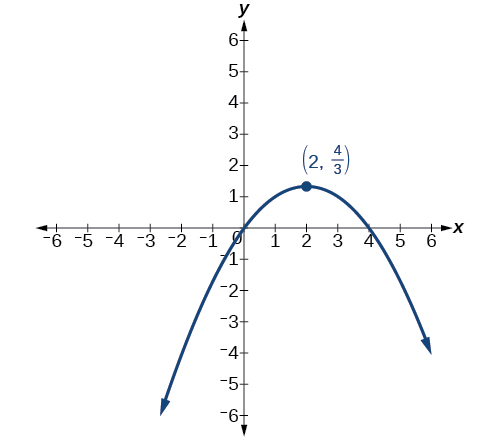
For the exercises 22-23, identify the conic with focus at the origin, and then give the directrix and eccentricity.
22) \(r=\dfrac{3}{2-\sin \theta }\)
23) \(r=\dfrac{5}{4+6\cos \theta }\)
- Answer
-
Hyperbola with \(e=\dfrac{3}{2}\) and directrix \(\dfrac{5}{6}\) units to the right of the pole.
For the exercises 24-26, graph the given conic section. If it is a parabola, label vertex, focus, and directrix. If it is an ellipse or a hyperbola, label vertices and foci.
24) \(r=\dfrac{12}{4-8\sin \theta }\)
25) \(r=\dfrac{2}{4+4\sin \theta }\)
- Answer
-
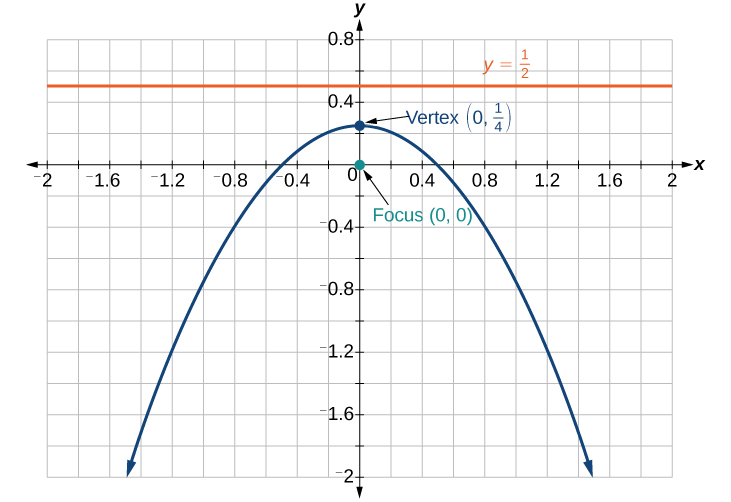
26) Find a polar equation of the conic with focus at the origin, eccentricity of \(e=2\), and directrix: \(x=3\).
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


