12.4: Derivatives
- Page ID
- 1406
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The average teen in the United States opens a refrigerator door an estimated 25 times per day. Supposedly, this average is up from 10 years ago when the average teenager opened a refrigerator door 20 times per day1. It is estimated that a television is on in a home 6.75 hours per day, whereas parents spend an estimated 5.5 minutes per day having a meaningful conversation with their children. These averages, too, are not the same as they were 10 years ago, when the television was on an estimated 6 hours per day in the typical household, and parents spent 12 minutes per day in meaningful conversation with their kids. What do these scenarios have in common? The functions representing them have changed over time. In this section, we will consider methods of computing such changes over time.
Finding the Average Rate of Change of a Function
The functions describing the examples above involve a change over time. Change divided by time is one example of a rate. The rates of change in the previous examples are each different. In other words, some changed faster than others. If we were to graph the functions, we could compare the rates by determining the slopes of the graphs.
A tangent line to a curve is a line that intersects the curve at only a single point but does not cross it there. (The tangent line may intersect the curve at another point away from the point of interest.) If we zoom in on a curve at that point, the curve appears linear, and the slope of the curve at that point is close to the slope of the tangent line at that point.
Figure \(\PageIndex{1}\) represents the function \(f(x)=x^3−4x\). We can see the slope at various points along the curve.
- slope at \(x=−2\) is 8
- slope at \(x=−1\) is –1
- slope at \(x=2\) is 8
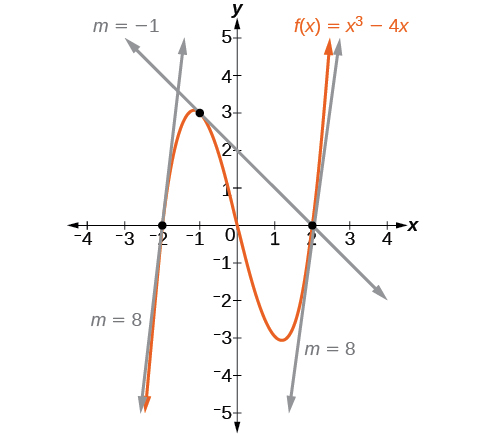
Let’s imagine a point on the curve of function \(f\) at \(x=a\) as shown in Figure \(\PageIndex{1}\). The coordinates of the point are \((a,f(a))\). Connect this point with a second point on the curve a little to the right of \(x=a\), with an x-value increased by some small real number \(h\). The coordinates of this second point are \((a+h,f(a+h))\) for some positive-value \(h\).
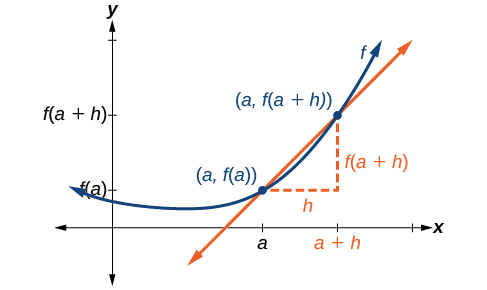
We can calculate the slope of the line connecting the two points \((a,f(a))\) and \((a+h,f(a+h))\), called a secant line, by applying the slope formula,
\[ \mathrm{slope = \dfrac{change \; in \; y}{change \; in \; x}} \]
We use the notation \(m_{sec}\) to represent the slope of the secant line connecting two points.
\[\begin{align} m_{sec} &= \dfrac{f(a+h)−f(a)}{(a+h)−(a) } \\ &= \dfrac{f(a+h)−f(a)}{\cancel{a}+h−\cancel{a}} \end{align}\]
The slope \(m_{sec}\) equals the average rate of change between two points \((a,f(a))\) and \((a+h,f(a+h)).\)
\[m_{sec}=\dfrac{f(a+h)−f(a)}{h}\]
the AVERAGE RATE OF CHANGE BETWEEN TWO POINTS ON A CURVE
The average rate of change (AROC) between two points \((a,f(a))\) and \((a+h,f(a+h))\) on the curve of \(f\) is the slope of the line connecting the two points and is given by
\[\text{AROC}=\dfrac{f(a+h)−f(a)}{h}\]
Example \(\PageIndex{1}\): Finding the Average Rate of Change
Find the average rate of change connecting the points \((2,−6)\) and \((−1,5)\).
Solution
We know the average rate of change connecting two points may be given by
\[\text{AROC}=\dfrac{f(a+h)−f(a)}{h}\]
If one point is \((2,−6)\), or \((2,f(2))\), then \(f(2)=−6.\)
The value \(h\) is the displacement from \(2\) to \(−1\), which equals \(−1−2=−3.\)
For the other point, \(f(a+h)\) is the y-coordinate at \(a+h\), which is \(2+(−3)\) or \(−1,\) so \(f(a+h)=f(−1)=5\).
\[\begin{align} \text{AROC} &= \dfrac{f(a+h)−f(a)}{h} \\ &=\dfrac{5−(−6)}{−3} \\&=\dfrac{11}{−3} \\ &=−\dfrac{11}{3} \end{align}\]
Exercise \(\PageIndex{1}\)
Find the average rate of change connecting the points \((−5,1.5)\) and \((−2.5,9)\)
Solution
3
Understanding the Instantaneous Rate of Change
Now that we can find the average rate of change, suppose we make \(h\) in Figure \(\PageIndex{2}\) smaller and smaller. Then \(a+h\) will approach \(a\) as \(h\) gets smaller, getting closer and closer to 0. Likewise, the second point \((a+h,f(a+h))\) will approach the first point, \((a,f(a))\). As a consequence, the connecting line between the two points, called the secant line, will get closer and closer to being a tangent to the function at \(x=a\), and the slope of the secant line will get closer and closer to the slope of the tangent at \(x=a\) (Figure \(\PageIndex{3}\)).
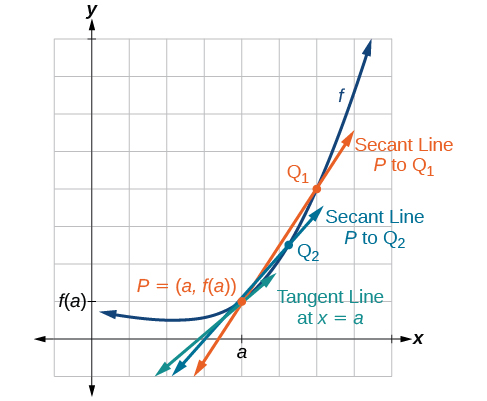
Because we are looking for the slope of the tangent at \(x=a\), we can think of the measure of the slope of the curve of a function \(f\) at a given point as the rate of change at a particular instant. We call this slope the instantaneous rate of change, or the derivative of the function at \(x=a.\) Both can be found by finding the limit of the slope of a line connecting the point at \(x=a\) with a second point infinitesimally close along the curve. For a function \(f\) both the instantaneous rate of change of the function and the derivative of the function at \(x=a\) are written as \(f'(a),\) and we can define them as a two-sided limit that has the same value whether approached from the left or the right.
\[f′(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h}\]
The expression by which the limit is found is known as the difference quotient.
DEFINITION OF INSTANTANEOUS RATE OF CHANGE AND DERIVATIVE
The derivative, or instantaneous rate of change, of a function \(f\) at \(x=a\), is given by
\[ f'(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h}\]
The expression \(\frac{f(a+h)−f(a)}{h}\) is called the difference quotient.
We use the difference quotient to evaluate the limit of the rate of change of the function as \(h\) approaches 0.
Derivatives: Interpretations and Notation
The derivative of a function can be interpreted in different ways. It can be observed as the behavior of a graph of the function or calculated as a numerical rate of change of the function.
- The derivative of a function \(f(x)\) at a point \(x=a\) is the slope of the tangent line to the curve \(f(x)\) at \(x=a\). The derivative of \(f(x)\) at \(x=a\) is written \(f′(a)\).
- The derivative \(f′(a)\) measures how the curve changes at the point \((a,f(a))\).
- The derivative \(f′(a)\) may be thought of as the instantaneous rate of change of the function \(f(x)\) at \(x=a\).
- If a function measures distance as a function of time, then the derivative measures the instantaneous velocity at time \(t=a\).
NOTATIONS FOR THE DERIVATIVE
The equation of the derivative of a function \(f(x)\) is written as \(y′=f′(x)\), where \(y=f(x)\). The notation \(f′(x)\) is read as “\(f\) prime of \(x\).” Alternate notations for the derivative include the following:
\[f′(x)=y′=\dfrac{dy}{dx}=\dfrac{df}{dx}=\dfrac{d}{dx} f(x)=Df(x)\]
The expression \(f′(x)\) is now a function of \(x\); this function gives the slope of the curve \(y=f(x)\) at any value of \(x\). The derivative of a function \(f(x)\) at a point \(x=a\) is denoted \(f′(a)\).
how to: Given a function \(f\), find the derivative by applying the definition of the derivative.
- Calculate \(f(a+h)\).
- Calculate \(f(a)\).
- Substitute and simplify \(\frac{f(a+h)−f(a)}{h}\).
- Evaluate the limit if it exists: \(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}\).
Example \(\PageIndex{1}\): Finding the Derivative of a Polynomial Function
Find the derivative of the function \(f(x)=x^2−3x+5\) at \(x=a.\)
Solution
We have:
\[ f′(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \;\;\;\;\;\;\;\; \text{Definition of a derivative}\]
Substitute \(f(a+h)=(a+h)^2−3(a+h)+5\) and \(f(a)=a^2−3a+5.\)
\[ \begin{align} f′(a) &= \lim \limits_{h \to 0} \dfrac{(a+h)(a+h)−3(a+h)+5−(a^2−3a+5)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{a^2+2ah+h^2−3a−3h+5−a^2+3a−5}{h} && \text{Evaluate to remove parentheses.} \\ & = \lim \limits_{h \to 0} \dfrac{\cancel{a^2}+2ah+h^2−\cancel{3a}−3h+\cancel{5}−\cancel{a^2}+\cancel{3a}−\cancel{5}}{h} && \text{Simplify.} \\ & = \lim \limits_{h \to 0} \dfrac{2ah+h^2−3h}{h} && \text{Factor out an }h. \\ & =2a+0−3 && \text{Evaluate the limit.} \\ &=2a−3 \end{align} \]
Exercise \(\PageIndex{1}\)
Find the derivative of the function \(f(x)=3x^2+7x\) at \(x=a\)
Solution
\(f′(a)=6a+7\)
Finding Derivatives of Rational Functions
To find the derivative of a rational function, we will sometimes simplify the expression using algebraic techniques we have already learned.
Example \(\PageIndex{1}\): Finding the Derivative of a Rational Function
Find the derivative of the function\(f(x)=\dfrac{3+x}{2−x}\) at \(x=a.\)
\[\begin{align} f′(a) &= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{\frac{3+(a+h)}{2−(a+h)}−(\frac{3+a}{2−a})}{h} && \text{Substitute }f(a+h) \text{ and }f(a) \\ &= \lim \limits_{h \to 0} \dfrac{(2−(a+h))(2−a)[ \frac{3+(a+h)}{2−(a+h)}−(\frac{3+a}{2−a}) ]}{(2−(a+h))(2−a)(h)} && \text{Multiply numerator and denominator by } (2−(a+h))(2−a) \\ & =\lim \limits_{h \to 0}\dfrac{(\cancel{2−(a+h)})(2−a)(\frac{3+(a+h)}{\cancel{(2−(a+h))}})−(2−(a+h))\cancel{(2−a)}(\frac{3+a}{\cancel{2−a}})}{(2−(a+h))(2−a)(h)} && \text{Distribute} \\ & =\lim \limits_{h \to 0} \dfrac{6−3a+2a−a^2+2h−ah−6+3a+3h−2a+a^2+ah}{(2−(a+h))(2−a)(h)} && \text{Multiply} \\ &=\lim \limits_{h \to 0} \dfrac{5 \cancel{h}}{(2−(a+h))(2−a)(\cancel{h})} && \text{Combine like terms} \\ & = \lim \limits_{h \to 0} \dfrac{5}{(2−(a+h))(2−a)} && \text{Cancel like factors} \\ & =\dfrac{5}{(2−(a+0))(2−a)}=\dfrac{5}{(2−a)(2−a)}=\dfrac{5}{(2−a)^2} && \text{Evaluate the limit} \end{align}\]
Exercise \(\PageIndex{1}\):
Find the derivative of the function \(f(x)=\frac{10x+11}{5x+4}\) at \(x=a\).
\[f′(a)=\dfrac{−15}{(5a+4)^2}\]
Finding Derivatives of Functions with Roots
To find derivatives of functions with roots, we use the methods we have learned to find limits of functions with roots, including multiplying by a conjugate.
Example \(\PageIndex{1}\): Finding the Derivative of a Function with a Root
Find the derivative of the function \(f(x)=4\sqrt{x}\) at \(x=36.\)
We have
\[\begin{align} f′(a) &=\lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{4\sqrt{a+h}−4\sqrt{a}}{h} && \text{Substitute }f(a+h) \text{ and }f(a) \end{align}\]
Multiply the numerator and denominator by the conjugate: \(\frac{4\sqrt{a+h}+4\sqrt{a}}{4\sqrt{a+h}+4\sqrt{a}}\).
\[\begin{align} f′(a) &= \lim \limits_{h \to 0}\bigg( \dfrac{4\sqrt{a+h}−4\sqrt{a}}{h} \bigg)⋅ \bigg(\dfrac{4\sqrt{a+h}+4\sqrt{a}}{4\sqrt{a+h}+4\sqrt{a}} \bigg) \\ &=\lim \limits_{h \to 0} \bigg( \dfrac{16(a+h)−16a}{h4(\sqrt{a+h}+4\sqrt{a})} \bigg) && \text{Multiply.} \\ &=\lim \limits_{ h \to 0} \bigg( \dfrac{\cancel{16a}+16h\cancel{−16a}}{h4(\sqrt{a+h}+4\sqrt{a})} \bigg) && \text{Distribute and combine like terms.} \\ &= \lim \limits_{h \to 0}\bigg(\dfrac{16\cancel{h}}{\cancel{h}(4\sqrt{a+h}+4\sqrt{a})} \bigg) && \text{Simplify.} \\ & = \lim \limits_{h \to 0} \bigg( \dfrac{16}{4\sqrt{a+h}+4\sqrt{a}} \bigg) && \text{Evaluate the limit by letting } h=0. \\ & =\dfrac{16}{8\sqrt{a}}=\dfrac{2}{\sqrt{a}} \\ f′(36) &= \dfrac{2}{\sqrt{36}} && \text{Evaluate the derivative at } x=36. \\ &=\dfrac{2}{6} \\ & =\dfrac{1}{3} \end{align}\]
Exercise \(\PageIndex{1}\):
Find the derivative of the function \(f(x)=9\sqrt{x}\) at \(x=9.\)
\(\frac{3}{2}\)
Finding Instantaneous Rates of Change
Many applications of the derivative involve determining the rate of change at a given instant of a function with the independent variable time—which is why the term instantaneous is used. Consider the height of a ball tossed upward with an initial velocity of 64 feet per second, given by \(s(t)=−16t^2+64t+6\), where \(t\) is measured in seconds and \(s(t)\) is measured in feet. We know the path is that of a parabola. The derivative will tell us how the height is changing at any given point in time. The height of the ball is shown in Figure as a function of time. In physics, we call this the “s-t graph.”
Example \(\PageIndex{1}\): Finding the Instantaneous Rate of Change
Using the function above, \(s(t)=−16t^2+64t+6\),what is the instantaneous velocity of the ball at 1 second and 3 seconds into its flight?
The velocity at \(t=1\) and \(t=3\) is the instantaneous rate of change of distance per time, or velocity. Notice that the initial height is 6 feet. To find the instantaneous velocity, we find the derivative and evaluate it at \(t=1\) and \(t=3\):
\[\begin{align} f′(a) &= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{−16(t+h)^2+64(t+h)+6−(−16t^2+64t+6)}{h} && \text{Substitute } s(t+h) \text{ and } s(t). \\ &= \lim \limits_{h \to 0} \dfrac{−16t^2−32ht−h^2+64t+64h+6+16t^2−64t−6}{h} && \text{Distribute} \\ & =\lim \limits_{h \to 0} \dfrac{−32ht−h^2+64h}{h} && \text{Simplify.} \\ &= \lim \limits_{h \to 0} \dfrac{\cancel{h}(−32t−h+64)}{\cancel{h}} && \text{Factor the numerator.} \\ & =\lim \limits_{h \to 0}−32t−h+64 && \text{ Cancel out the common factor} h. \\ s′(t) &=−32t+64 && \text{Evaluate the limit by letting} h=0. \end{align}\]
For any value of \(t\), \(s′(t)\) tells us the velocity at that value of \(t\).
Evaluate \(t=1\) and \(t=3\).
\[\begin{align}s′(1) &=−32(1)+64=32 \\ s′(3) &=−32(3)+64=−32 \end{align}\]
The velocity of the ball after 1 second is 32 feet per second, as it is on the way up.
The velocity of the ball after 3 seconds is −32 feet per second, as it is on the way down.
Exercise \(\PageIndex{1}\):
The position of the ball is given by\(s(t)=−16t^2+64t+6.\) What is its velocity 2 seconds into flight?
0
Using Graphs to Find Instantaneous Rates of Change
We can estimate an instantaneous rate of change at \(x=a\) by observing the slope of the curve of the function \(f(x)\) at \(x=a\). We do this by drawing a line tangent to the function at \(x=a\) and finding its slope.
how to: Given a graph of a function \(f( x )\), find the instantaneous rate of change of the function at \(x=a\).
- Locate \(x=a\) on the graph of the function \(f(x)\).
- Draw a tangent line, a line that goes through \(x=a\) at \(a\) and at no other point in that section of the curve. Extend the line far enough to calculate its slope as
\[\dfrac{\text{change in }y}{\text{change in }x.}\]
Example \(\PageIndex{1}\): Estimating the Derivative at a Point on the Graph of a Function
From the graph of the function \(y=f(x)\) presented in Figure, estimate each of the following:
\(f(0) ; f(2) ; f'(0) ; f'(2)\)
To find the functional value, \(f(a)\), find the y-coordinate at \(x=a\).
To find the derivative at \(x=a, f′(a),\) draw a tangent line at \(x=a,\) and estimate the slope of that tangent line. See Figure.
- \(f(0)\) is the y-coordinate at \(x=0\). The point has coordinates \((0,1)\), thus \(f(0)=1\).
- \(f(2)\) is the y-coordinate at \(x=2\). The point has coordinates \((2,1)\), thus \(f(2)=1\).
- \(f′(0)\) is found by estimating the slope of the tangent line to the curve at \(x=0\). The tangent line to the curve at \(x=0\) appears horizontal. Horizontal lines have a slope of 0, thus \(f′(0)=0\).
- \(f′(2)\) is found by estimating the slope of the tangent line to the curve at \(x=2\). Observe the path of the tangent line to the curve at \(x=2\). As the \(x\) value moves one unit to the right, the \(y\) value moves up four units to another point on the line. Thus, the slope is 4, so \(f′(2)=4\).
Exercise \(\PageIndex{1}\):
Using the graph of the function\(f(x)=x^3−3x\) shown in Figure, estimate: \(f(1), f′(1), f(0)\),and \(f′(0)\).
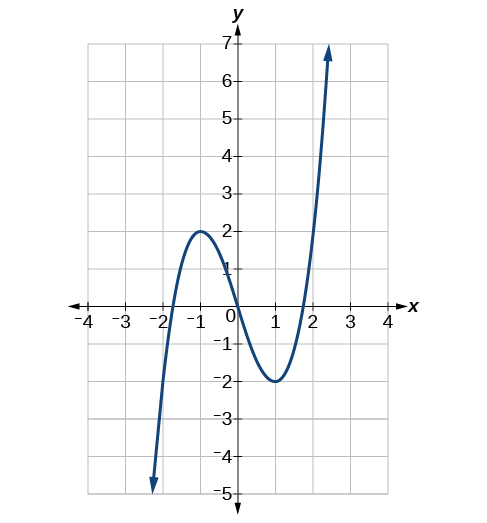
−2,−2,0, 0, −3
Using Instantaneous Rates of Change to Solve Real-World Problems
Another way to interpret an instantaneous rate of change at \(x=a\) is to observe the function in a real-world context. The unit for the derivative of a function \(f(x)\) is
\[\dfrac{\text{output units}}{\text{input unit}}\]
Such a unit shows by how many units the output changes for each one-unit change of input. The instantaneous rate of change at a given instant shows the same thing: the units of change of output per one-unit change of input.
One example of an instantaneous rate of change is a marginal cost. For example, suppose the production cost for a company to produce \(x\) items is given by \(C(x)\), in thousands of dollars. The derivative function tells us how the cost is changing for any value of \(x\) in the domain of the function. In other words, \(C′(x)\) is interpreted as a marginal cost, the additional cost in thousands of dollars of producing one more item when \(x\) items have been produced. For example, \(C′(11)\) is the approximate additional cost in thousands of dollars of producing the 12th item after 11 items have been produced. \(C′(11)=2.50\) means that when 11 items have been produced, producing the 12th item would increase the total cost by approximately $2,500.00.
Example \(\PageIndex{1}\): Finding a Marginal Cost
The cost in dollars of producing \(x\) laptop computers in dollars is \(f(x)=x^2−100x.\) At the point where 200 computers have been produced, what is the approximate cost of producing the 201stunit?
If \(f(x)=x^2−100x\) describes the cost of producing \(x\) computers, \(f′(x)\) will describe the marginal cost. We need to find the derivative. For purposes of calculating the derivative, we can use the following functions:
\[\begin{align} f(a+b) &=(x+h)^2−100(x+h) \\ f(a) &=a ^2−100a \end{align}\]
\[\begin{align} f′(x) &=\dfrac{f(a+h)−f(a)}{h} && \text{Formula for a derivative} \\ &=\dfrac{(x+h)^2−100(x+h)−(x^2−100x)}{h} \\ \text{Substitute }f(a+h) \text{ and }f(a). \\ & =\dfrac{x^2+2xh+h^2−100x−100h−x^2+100x}{h} && \text{Multiply polynomials, distribute.} \\ &= \text{2xh+h^2−100h}{h} && \text{Collect like terms.} \\ &=\dfrac{\cancel{h}(2x+h−100)}{\cancel{h}} && \text{Factor and cancel like terms.} \\ &=2x+h−100 && \text{Simplify.} \\ &=2x−100 && \text{Evaluate when }h=0. \\ f′(x) &=2x−100 && \text{Formula for marginal cost} \\ f′(200) &=2(200)−100=300 && \text{Evaluate for 200 units.} \end{align}\]
The marginal cost of producing the 201st unit will be approximately $300.
Example \(\PageIndex{1}\):Interpreting a Derivative in Context
A car leaves an intersection. The distance it travels in miles is given by the function \( f(t)\), where \(t\) represents hours. Explain the following notations:
\(f(0)=0 f′(1)=60 f(1)=70 f(2.5)=150\)
First we need to evaluate the function \(f(t)\) and the derivative of the function \(f′(t)\), and distinguish between the two. When we evaluate the function \(f(t)\), we are finding the distance the car has traveled in \(t\) hours. When we evaluate the derivative f′(t), f′(t), we are finding the speed of the car after \(t\) hours.
- \(f(0)=0\) means that in zero hours, the car has traveled zero miles.
- \(f′(1)=60\) means that one hour into the trip, the car is traveling 60 miles per hour.
- \(f(1)=70\) means that one hour into the trip, the car has traveled 70 miles. At some point during the first hour, then, the car must have been traveling faster than it was at the 1-hour mark.
- \(f(2.5)=150\) means that two hours and thirty minutes into the trip, the car has traveled 150 miles.
Exercise \(\PageIndex{1}\)
A runner runs along a straight east-west road. The function \(f(t)\) gives how many feet eastward of her starting point she is after \(t\) seconds. Interpret each of the following as it relates to the runner.
\(f(0)=0 ; f(10)=150 ; f′(10)=15 ; f′(20)=−10 ; f(40)=−100\)
- After zero seconds, she has traveled 0 feet.
- After 10 seconds, she has traveled 150 feet east.
- After 10 seconds, she is moving eastward at a rate of 15 ft/sec.
- After 20 seconds, she is moving westward at a rate of 10 ft/sec.
- After 40 seconds, she is 100 feet westward of her starting point.
Finding Points Where a Function’s Derivative Does Not Exist
To understand where a function’s derivative does not exist, we need to recall what normally happens when a function \(f(x)\) has a derivative at \(x=a\). Suppose we use a graphing utility to zoom in on \(x=a\). If the function \(f(x)\) is differentiable, that is, if it is a function that can be differentiated, then the closer one zooms in, the more closely the graph approaches a straight line. This characteristic is called linearity.
Look at the graph in Figure. The closer we zoom in on the point, the more linear the curve appears.
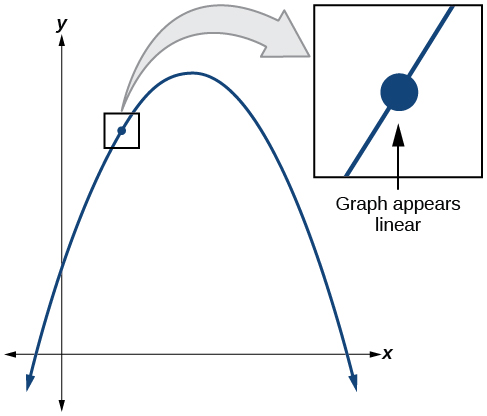
Graph of the function \(f(x)=| x |\),with x-axis from –0.1 to 0.1 and y-axis from –0.1 to 0.1.
What are the characteristics of a graph that is not differentiable at a point? Here are some examples in which function \(f(x)\) is not differentiable at \(x=a\).
In Figure, we see the graph of
\[f(x)=\begin{cases} x^2, &&x≤2 \\ 8−x, &&x>2.\end{cases} .\]
Notice that, as \(x\) approaches 2 from the left, the left-hand limit may be observed to be 4, while as \(x\) approaches 2 from the right, the right-hand limit may be observed to be 6. We see that it has a discontinuity at \(x=2\).
The graph of \(f(x)\) has a discontinuity at \(x=2\).
In Figure, we see the graph of \(f(x)=|x|\). We see that the graph has a corner point at \(x=0\).
The graph of \(f(x)=| x |\) has a corner point at \(x=0\).
In Figure, we see that the graph of \(f(x)=x^{\frac{2}{3}}\) has a cusp at \(x=0\). A cusp has a unique feature. Moving away from the cusp, both the left-hand and right-hand limits approach either infinity or negative infinity. Notice the tangent lines as \(x\) approaches 0 from both the left and the right appear to get increasingly steeper, but one has a negative slope, the other has a positive slope.
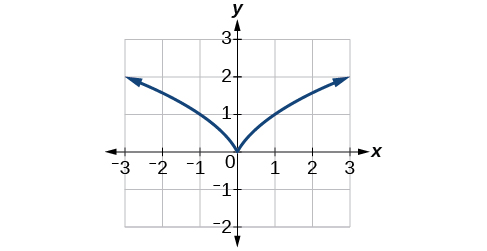
The graph of \(f(x)=x^\frac{2}{3}\) has a cusp at \(x=0\).
In Figure, we see that the graph of \(f(x)=x^{frac{1}{3}}\) has a vertical tangent at \(x=0\). Recall that vertical tangents are vertical lines, so where a vertical tangent exists, the slope of the line is undefined. This is why the derivative, which measures the slope, does not exist there.
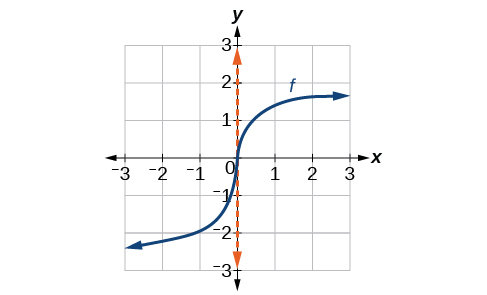
The graph of \(f(x)=x^\frac{1}{3}\) has a vertical tangent at \(x=0\).
differentiability
A function \(f(x)\) is differentiable at \(x=a\) if the derivative exists at \(x=a\),which means that \(f′(a)\) exists.
There are four cases for which a function \(f(x)\) is not differentiable at a point \(x=a\).
- When there is a discontinuity at \(x=a\).
- When there is a corner point at \(x=a\).
- When there is a cusp at \(x=a\).
- Any other time when there is a vertical tangent at \(x=a\).
Example \(\PageIndex{1}\): Determining Where a Function Is Continuous and Differentiable from a Graph
Using Figure, determine where the function is
- continuous
- discontinuous
- differentiable
- not differentiable
At the points where the graph is discontinuous or not differentiable, state why.
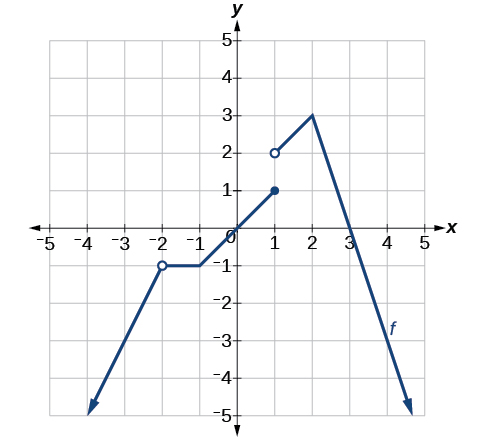
Three intervals where the function is continuous
The graph of is differentiable on \((−∞,−2)∪(−2,−1)∪(−1,1)∪(1,2)∪(2,∞)\). The graph of \(f(x)\) is not differentiable at \(x=−2\) because it is a point of discontinuity, at \(x=−1\) because of a sharp corner, at \(x=1\) because it is a point of discontinuity, and at \(x=2\) because of a sharp corner. See Figure.
Five intervals where the function is differentiable
Exercise \(\PageIndex{1}\):
Determine where the function \(y=f(x)\) shown in Figure is continuous and differentiable from the graph.
The graph of \(f\) is continuous on \((−∞,1)∪(1,3)∪(3,∞).\) The graph of f f is discontinuous at \(x=1\) and \(x=3\). The graph of \(f\) is differentiable on \((−∞,1)∪(1,3)∪(3,∞)\). The graph of \(f\) is not differentiable at \(x=1\) and \(x=3\).
Finding an Equation of a Line Tangent to the Graph of a Function
The equation of a tangent line to a curve of the function \(f(x)\) at \(x=a\) is derived from the point-slope form of a line, \(y=m(x−x_1)+y_1\). The slope of the line is the slope of the curve at \(x=a\) and is therefore equal to \(f′(a),\) the derivative of \(f(x)\) at \(x=a.\) The coordinate pair of the point on the line at \(x=a\) is \((a,f(a))\).
If we substitute into the point-slope form, we have
The equation of the tangent line is
\[y=f'(a)(x−a)+f(a)\]
F
The equation of a line tangent to the curve of a function \(f\) at a point \(x=a\) is
\[y=f'(a)(x−a)+f(a)\]
how to: Given a function \(f\), find the equation of a line tangent to the function at \(x=a\).
- Find the derivative of \(f(x)\) at \(x=a\) using \(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}.\)
- Evaluate the function at \(x=a\). This is \(f(a)\).
- Substitute \((a,f(a))\) and \(f′(a)\) into \(y=f'(a)(x−a)+f(a)\).
- Write the equation of the tangent line in the form \(y=mx+b\).
Example \(\PageIndex{1}\): Finding the Equation of a Line Tangent to a Function at a Point
Find the equation of a line tangent to the curve \(f(x)=x^2−4x\) at \(x=3.\)
Using:
\[f'(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h}\]
Substitute \(f(a+h)=(a+h)^2−4(a+h)\) and \(f(a)=a^2−4a.\)
\[\begin{align} f′(a) &= \lim \limits_{h \to 0}\dfrac{(a+h)(a+h)−4(a+h)−(a2−4a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{a^2+2ah+h^2−4a−4h−a^2+4a}{h} && \text{Remove parentheses.} \\ &= \lim \limits_{h \to 0} \dfrac{\cancel{a^2}+2ah+h^2−\cancel{4a}−4h−\cancel{a^2}+\cancel{4a}}{h} && \text{Combine like terms.} \\ &= \lim \limits_{h \to 0} \dfrac{2ah+h^2−4h}{h} \\ &= \lim \limits_{h \to 0} \dfrac{\cancel{h}(2a+h−4)}{h} && \text{Factor out }h. \\ &=2a+0−4 \\ f′(a)&=2a−4 && \text{Evaluate the limit.} \\ f′(3)&=2(3)−4=2 \end{align}\]
Equation of tangent line at \(x=3\):
\[\begin{align} y &= f'(a)(x−a)+f(a) \\ y &=f'(3)(x−3)+f(3) \\ y &=2(x−3)+(−3) \\ y &=2x−9 \end{align}\]
Analysis
We can use a graphing utility to graph the function and the tangent line. In so doing, we can observe the point of tangency at \(x=3\) as shown in Figure.
Graph confirms the point of tangency at \(x=3\).
Exercise \(\PageIndex{1}\):
Find the equation of a tangent line to the curve of the function \(f(x)=5x^2−x+4\) at \(x=2\).
\(y=19x−16\)
Finding the Instantaneous Speed of a Particle
If a function measures position versus time, the derivative measures displacement versus time, or the speed of the object. A change in speed or direction relative to a change in time is known as velocity. The velocity at a given instant is known as instantaneous velocity.
In trying to find the speed or velocity of an object at a given instant, we seem to encounter a contradiction. We normally define speed as the distance traveled divided by the elapsed time. But in an instant, no distance is traveled, and no time elapses. How will we divide zero by zero? The use of a derivative solves this problem. A derivative allows us to say that even while the object’s velocity is constantly changing, it has a certain velocity at a given instant. That means that if the object traveled at that exact velocity for a unit of time, it would travel the specified distance.
INSTANTANEOUS VELOCITY
Let the function \(s(t)\) represent the position of an object at time \(t.\) The instantaneous velocity or velocity of the object at time \(t=a\) is given by
\[s′(a)= \lim \limits_{h \to 0} \dfrac{s(a+h)−s(a)}{h}\]
Example \(\PageIndex{1}\): Finding the Instantaneous Velocity
A ball is tossed upward from a height of 200 feet with an initial velocity of 36 ft/sec. If the height of the ball in feet after \(t\) seconds is given by \(s(t)=−16t^2+36t+200,\) find the instantaneous velocity of the ball at \( t=2\).
First, we must find the derivative \(s′(t)\). Then we evaluate the derivative at \(t=2\), using \(s(a+h)=−16(a+h)^2+36(a+h)+200\) and \(s(a)=−16a^2+36a+200.\)
\[\begin{align} s′(a)= \lim \limits_{h \to 0} \dfrac{s(a+h)−s(a)}{h} \\ &= \lim \limits_{h \to 0}\dfrac{−16(a+h)^2+36(a+h)+200−(−16a^2+36a+200)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{−16(a^2+2ah+h^2)+36(a+h)+200−(−16a^2+36a+200)}{h} \\ &= \lim \limits_{h \to 0}\dfrac{−16a^2−32ah−16h^2+36a+36h+200+16a^2−36a−200}{h} \\ &= \lim \limits_{h \to 0}\dfrac{\cancel{−16a^2}−32ah−16h^2+\cancel{36a}+36h+\cancel{200}+\cancel{16a^2}−\cancel{36a}−\cancel{200}}{h} \\ &= \lim \limits_{h \to 0}\dfrac{−32ah−16h^2+36h}{h} \\ &= \lim \limits_{h \to 0}\dfrac{\cancel{h}(−32a−16h+36)}{\cancel{h}} \\ &= \lim \limits_{h \to 0}(−32a−16h+36) \\&=−32a−16⋅0+36 \\ s′(a) &=−32a+36 \\ s′(2) &=−32(2)+36 \\ & =−28 \end{align}\]
Analysis
This result means that at time \(t=2\) seconds, the ball is dropping at a rate of 28 ft/sec.
Exercise \(\PageIndex{1}\):
A fireworks rocket is shot upward out of a pit 12 ft below the ground at a velocity of 60 ft/sec. Its height in feet after \(t\) seconds is given by \(s=−16t^2+60t−12.\) What is its instantaneous velocity after 4 seconds?
–68 ft/sec, it is dropping back to Earth at a rate of 68 ft/s.
Access these online resources for additional instruction and practice with derivatives.
Visit this website for additional practice questions from Learningpod.
Key Equations
| average rate of change | \(\text{AROC}=\frac{f(a+h)−f(a)}{h}\) |
| derivative of a function | \(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}\) |
Key Concepts
- The slope of the secant line connecting two points is the average rate of change of the function between those points. See Example.
- The derivative, or instantaneous rate of change, is a measure of the slope of the curve of a function at a given point, or the slope of the line tangent to the curve at that point. See Example, Example, and Example.
- The difference quotient is the quotient in the formula for the instantaneous rate of change:
\(\frac{f(a+h)−f(a)}{h}\)
- Instantaneous rates of change can be used to find solutions to many real-world problems. See Example.
- The instantaneous rate of change can be found by observing the slope of a function at a point on a graph by drawing a line tangent to the function at that point. See Example.
- Instantaneous rates of change can be interpreted to describe real-world situations. See Example and Example.
- Some functions are not differentiable at a point or points. See Example.
- The point-slope form of a line can be used to find the equation of a line tangent to the curve of a function. See Example.
- Velocity is a change in position relative to time. Instantaneous velocity describes the velocity of an object at a given instant. Average velocity describes the velocity maintained over an interval of time.
- Using the derivative makes it possible to calculate instantaneous velocity even though there is no elapsed time. See Example.
Section Exercises
Verbal
How is the slope of a linear function similar to the derivative?
The slope of a linear function stays the same. The derivative of a general function varies according to \(x\). Both the slope of a line and the derivative at a point measure the rate of change of the function.
What is the difference between the average rate of change of a function on the interval \([ x,x+h ]\) and the derivative of the function at \(x\)?
A car traveled 110 miles during the time period from 2:00 P.M. to 4:00 P.M. What was the car's average velocity? At exactly 2:30 P.M., the speed of the car registered exactly 62 miles per hour. What is another name for the speed of the car at 2:30 P.M.? Why does this speed differ from the average velocity?
Average velocity is 55 miles per hour. The instantaneous velocity at 2:30 p.m. is 62 miles per hour. The instantaneous velocity measures the velocity of the car at an instant of time whereas the average velocity gives the velocity of the car over an interval.
Explain the concept of the slope of a curve at point \(x\).
Suppose water is flowing into a tank at an average rate of 45 gallons per minute. Translate this statement into the language of mathematics.
The average rate of change of the amount of water in the tank is 45 gallons per minute. If \(f(x)\) is the function giving the amount of water in the tank at any time \(t\),then the average rate of change of \(f(x)\) between \(t=a\) and \(t=b\) is \(f(a)+45(b−a).\)
Algebraic
For the following exercises, use the definition of derivative \(\lim \limits_{h to 0} \frac{f(x+h)−f(x)}{h}\) to calculate the derivative of each function.
\(f(x)=3x−4\)
\(f(x)=−2x+1\)
\(f′(x)=−2\)
\(f(x)=x^2−2x+1\)
\(f(x)=2x^2+x−3
\(f′(x)=4x+1\)
\(f(x)=2x^2+5\)
\(f(x)=\frac{−1}{x−2}\)
\(f′(x)=\frac{1}{(x−2)^2}\)
\(f(x)=\frac{2+x}{1−x}\)
\(f(x)=\frac{5−2x}{3+2x}\)
\(\frac{−16(}{3+2x)^2}\)
\(f(x)=\sqrt{1+3x}\)
\(f(x)=3x^3−x^2+2x+5\)
\(f′(x)=9x^2−2x+2\)
\(f(x)=5\)
\(f(x)=5π\)
\(f′(x)=0\)
For the following exercises, find the average rate of change between the two points.
\((−2,0)\) and \((−4,5)\)
\((4,−3)\) and \((−2,−1)\)
\(−\frac{1}{3}\)
\((0,5)\) and \((6,5)\)
\((7,−2)\) and \((7,10)\)
undefined
For the following polynomial functions, find the derivatives.
\(f(x)=x^3+1\)
\(f(x)=−3x^2−7x=6\)
\(f′(x)=−6x−7\)
\(f(x)=7x^2\)
\(f(x)=3x^3+2x^2+x−26\)
\(f′(x)=9x^2+4x+1\)
For the following functions, find the equation of the tangent line to the curve at the given point \(x\) on the curve.
\(f(x)=2x^2−3x \;\;\; x=3\)
\(f(x)=x^3+1 \;\;\;\; x=2\)
\(y=12x−15\)
\(f(x)=\sqrt{x} \;\;\;\; x=9\)
For the following exercise, find \(k\) such that the given line is tangent to the graph of the function.
\(f(x)=x^2−kx, \;\;\; y=4x−9\)
\(k=−10\) or \(k=2\)
Graphical
For the following exercises, consider the graph of the function \(f\) and determine where the function is continuous/discontinuous and differentiable/not differentiable.
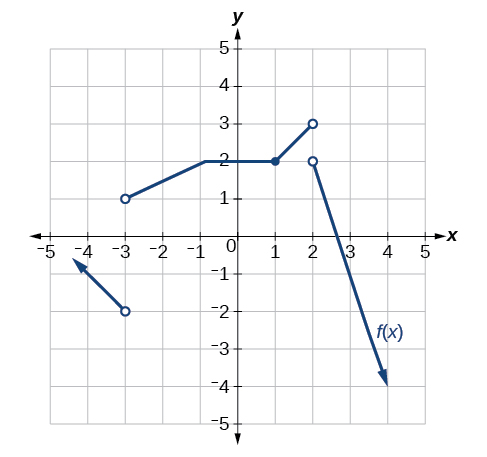
Discontinuous at \(x=−2\) and \(x=0\). Not differentiable at –2, 0, 2.
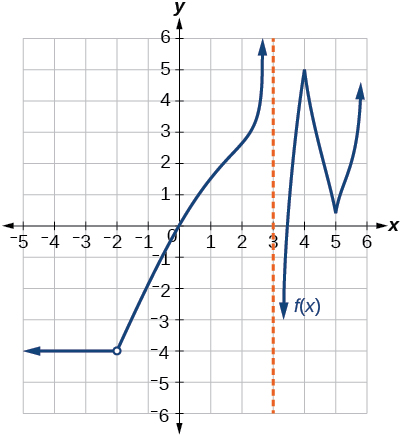
Discontinuous at \(x=5\). Not differentiable at -4, –2, 0, 1, 3, 4, 5.
For the following exercises, use Figure to estimate either the function at a given value of \(x\) or the derivative at a given value of \(x\), as indicated.
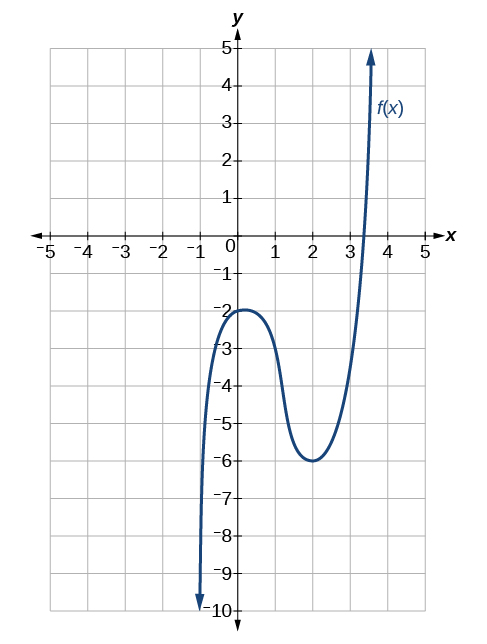
\(f(−1)\)
\(f(0)\)
\(f(0)=−2\)
\(f(1)\)
\(f(2)\)
\(f(2)=−6f(2)=−6
\(f(3)\)
\(f′(−1)\)
\(f′(−1)=9\)
\(f′(0)\)
\(f′(1)\)
\(f′(1)=−3\)
\(f′(2)\)
\(f′(3)\)
\(f′(3)=9\)
Sketch the function based on the information below:
\(f′(x)=2x, f(2)=4\)
Technology
Numerically evaluate the derivative. Explore the behavior of the graph of \(f(x)=x^2\) around \(x=1\) by graphing the function on the following domains: \([ 0.9,1.1 ], [ 0.99,1.01 ], [ 0.999,1.001 ],\) and \([0.9999, 1.0001]\). We can use the feature on our calculator that automatically sets Ymin and Ymax to the Xmin and Xmax values we preset. (On some of the commonly used graphing calculators, this feature may be called ZOOM FIT or ZOOM AUTO). By examining the corresponding range values for this viewing window, approximate how the curve changes at \(x=1,\) that is, approximate the derivative at \(x=1.\)
Answers vary. The slope of the tangent line near \(x=1\) is 2.
Real-World Applications
For the following exercises, explain the notation in words. The volume \(f(t)\) of a tank of gasoline, in gallons, \(t\) minutes after noon.
\(f(0)=600\)
\(f'(30)=−20\)
At 12:30 p.m., the rate of change of the number of gallons in the tank is –20 gallons per minute. That is, the tank is losing 20 gallons per minute.
\(f(30)=0\)
\(f'(200)=30\)
At 200 minutes after noon, the volume of gallons in the tank is changing at the rate of 30 gallons per minute.
\(f(240)=500\)
For the following exercises, explain the functions in words. The height, \(s\), of a projectile after \(t\) seconds is given by \(s(t)=−16t^2+80t.\)
\(s(2)=96\)
The height of the projectile after 2 seconds is 96 feet.
\(s'(2)=16\)
\(s(3)=96\)
The height of the projectile at \(t=3\) seconds is 96 feet.
\(s'(3)=−16\)
\(s(0)=0,s(5)=0.\)
The height of the projectile is zero at \(t=0\) and again at \(t=5\). In other words, the projectile starts on the ground and falls to earth again after 5 seconds.
For the following exercises, the volume \(V\) of a sphere with respect to its radius \(r\) is given by \(V=\frac{4}{3}πr^3.\)
Find the average rate of change of \(V\) as \(r\) changes from 1 cm to 2 cm.
Find the instantaneous rate of change of \(V\) when r=3 cm. r=3 cm.
\(36π\)
For the following exercises, the revenue generated by selling \(x\) items is given by \(R(x)=2x^2+10x\).
Find the average change of the revenue function as \(x\) changes from \(x=10\) to \(x=20\).
Find \(R'(10)\) and interpret.
$50.00 per unit, which is the instantaneous rate of change of revenue when exactly 10 units are sold.
Find \(R'(15)\) and interpret. Compare \(R'(15)\) to \(R'(10),\) and explain the difference.
For the following exercises, the cost of producing \(x\) cellphones is described by the function \(C(x)=x^2−4x+1000.\)
Find the average rate of change in the total cost as \(x\) changes from \(x=10\) to \(x=15.\)
$21 per unit
Find the approximate marginal cost, when 15 cellphones have been produced, of producing the 16th cellphone.
Find the approximate marginal cost, when 20 cellphones have been produced, of producing the 21st cellphone.
$36
Extension
For the following exercises, use the definition for the derivative at a point \(x=a\), \(\lim \limits_{x \to a}\frac{f(x)−f(a)}{x−a},\) to find the derivative of the functions.
\(f(x)=\frac{1}{x^2}\)
\(f(x)=5x^2−x+4\)
\(f'(x)=10a−1\)
\(f(x)=−x^2+4x+7\)
\(f(x)=\frac{−4}{3−x^2}\)
\(\frac{4}{(3−x)^2}\)
Chapter Review Exercises
Finding Limits: A Numerical and Graphical Approach
For the following exercises, use Figure.
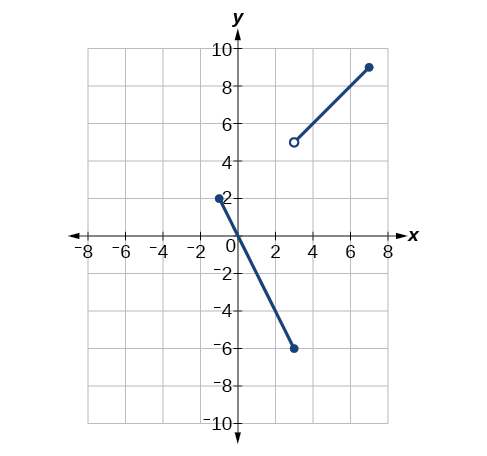
\(\lim \limits_{x \to −1^+}f(x)\)
2
\(\lim \limits_{x \to −1^−}f(x)\)
\(\lim \limits_{x \to −1} f(x)\)
does not exist
\(\lim \limits_{x \to 3}f(x)\)
At what values of \(x\) is the function discontinuous? What condition of continuity is violated?
Discontinuous at \(x=−1\) (\(\lim \limits_{x \to a} f(x)\) does not exist), \(x=3\) (jump discontinuity),and \(x=7\) ((\lim \limits_{x \to a} f(x)\) does not exist).
Using Table, estimate \(\lim \limits_{x \to 0}f(x).\)
| \(x\) | \(F(x)\) |
| −0.1 | 2.875 |
| −0.01 | 2.92 |
| −0.001 | 2.998 |
| 0 | Undefined |
| 0.001 | 2.9987 |
| 0.01 | 2.865 |
| 0.1 | 2.78145 |
| 0.15 | 2.678 |
3
For the following exercises, with the use of a graphing utility, use numerical or graphical evidence to determine the left- and right-hand limits of the function given as \(x\) approaches \(a\). If the function has limit as \(x\) approaches \(a\), state it. If not, discuss why there is no limit.
\(f(x)=\begin{cases} | x |−1, && \text{if }x≠1 \\ x^3, \text{if }x=1 \end{cases} a=1\)
\(f(x)=\begin{cases} \frac{1}{x+1}, && \text{if }x=−2 \\ (x+1)^2, && \text{if }x≠−2 \end{cases} a=−2\)
\(\lim \limits_{x \to −2} f(x)=1\)
\(f(x)= \begin{cases} \sqrt{x+3} && \text{if } x < 1 \\ −\sqrt[3]{x} && \text{if }x>1 \end{cases} a=1\)
Finding Limits: Properties of Limits
For the following exercises, find the limits if \(\lim \limits_{x \to c} f(x)=−3\) and \(\lim \limits_{x \to c} g(x)=5\).
\(\lim \limits_{x \to c} (f(x)+g(x))\)
2
\(\lim \limits_{x \to c} \frac{f(x)}{g(x)}\)
\(\lim \limits_{x to c}(f(x)⋅g(x))\)
\(−15\)
\(\lim \limits_{x \to 0^+}f(x),f(x)= \begin{cases} 3x^2+2x+1 && x>0 \\ 5x+3 && x<0 \end{cases}\)
\(\lim \limits_{x \to 0^-}f(x),f(x)= \begin{cases} 3x^2+2x+1 && x>0 \\ 5x+3 && x<0 \end{cases}\)
3
\(\lim \limits_{x \to 3^+}(3x−〚x〛)\)
For the following exercises, evaluate the limits using algebraic techniques.
\(\lim \limits_{h \to 0}(\frac{(h+6)^2−36}{h})\)
12
\(\lim \limits_{x \to 25}(\frac{x^2−625}{\sqrt{x}−5)}\)
\(\lim \limits_{x \to 1}(\frac{−x^2−9x}{x})\)
−10
\(\lim \limits_{x \to 4}\frac{7−\sqrt{12x+1}}{x−4}\)
\(\lim \limits_{x \to −3}(\frac{\frac{1}{3}+\frac{1}{x}}{3+x})\)
\(−\frac{1}{9}\)
Continuity
For the following exercises, use numerical evidence to determine whether the limit exists at \(x=a\). If not, describe the behavior of the graph of the function at \(x=a\).
\(f(x)=\frac{−2}{x−4}; a=4\)
\(f(x)=\frac{−2}{(x−4)^2}; a=4\)
At \(x=4\),the function has a vertical asymptote.
\(f(x)=\frac{−x}{x^2−x−6}; a=3\)
\(f(x)=\frac{6x^2+23x+20}{4x^2−25}; a=−\frac{5}{2}\)
removable discontinuity at \(a=−\frac{5}{2}\)
\(f(x)=\frac{\sqrt{x}−3}{9−x}; a=9\)
For the following exercises, determine where the given function \(f(x)\) is continuous. Where it is not continuous, state which conditions fail, and classify any discontinuities.
\(f(x)=x^2−2x−15\)
continuous on \((−∞,∞)\)
\(f(x)=\frac{x^2−2x−15}{x−5}\)
\(f(x)=\frac{x^2−2x}{x^2−4x+4}\)
removable discontinuity at \(x=2. f(2)\) is not defined, but limits exist.
\(f(x)=\frac{x^3−125}{2x^2−12x+10}\)
\(f(x)=\frac{x^2−\frac{1}{x}}{2−x}\)
discontinuity at \(x=0\) and \(x=2\). Both \(f(0)\) and \(f(2)\) are not defined.
\(f(x)=\frac{x+2}{x^2−3x−10}\)
\(f(x)=\frac{x+2}{x^3+8}\)
removable discontinuity at \(x=–2. f(–2)\) is not defined.
Derivatives
For the following exercises, find the average rate of change \(\frac{f(x+h)−f(x)}{h}\).
\(f(x)=3x+2\)
\(f(x)=5\)
0
\(f(x)=\frac{1}{x+1}\)
\(f(x)= \ln (x)\)
\(\frac{\ln (x+h)− \ln (x)}{h}\)
\(f(x)=e^{2x}\)
For the following exercises, find the derivative of the function.
\(f(x)=4x−6\)
\(=4\)
\(f(x)=5x^2−3x\)
Find the equation of the tangent line to the graph of \(f(x)\) at the indicated \(x\) value.
\(f(x)=−x^3+4x; x=2.\)
\(y=−8x+16\)
For the following exercises, with the aid of a graphing utility, explain why the function is not differentiable everywhere on its domain. Specify the points where the function is not differentiable.
\(f(x)=\frac{x}{| x |}\)
Given that the volume of a right circular cone is \(V=\frac{1}{3}πr^2h\) and that a given cone has a fixed height of 9 cm and variable radius length, find the instantaneous rate of change of volume with respect to radius length when the radius is 2 cm. Give an exact answer in terms of \(π\)
\(12π\)
Practice Test
For the following exercises, use the graph of \(f\) in Figure.
\(f(1)\)
3
\(\lim \limits_{x \to −1^+}f(x)\)
\(\lim \limits_{x \to −1^-}f(x)\)
0
\(\lim \limits_{x \to −1}f(x)\)
\(\lim \limits_{x \to −2}f(x)\)
\(−1\)
At what values of \(x\) is \(f\) discontinuous? What property of continuity is violated?
For the following exercises, with the use of a graphing utility, use numerical or graphical evidence to determine the left- and right-hand limits of the function given as \(x\) approaches \(a\). If the function has a limit as \(x\) approaches \(a\),state it. If not, discuss why there is no limit
\(f(x)=\begin{cases} \frac{1}{x}−3, && \text{if }x≤2 \\ x^3+1, && \text{if } x>2 \end{cases} a=2\)
\(\lim \limits_{x \to 2^−} f(x)=−\frac{5}{2}a\) and \(\lim \limits_{x \to 2^+} f(x)=9\) Thus, the limit of the function as \(x\) approaches 2 does not exist.
\(f(x)=\begin{cases} x^3+1, && \text{if }x<1 \\ 3x^2−1, && \text{if } x=1 \\ −\sqrt{x+3}+4, && \text{if } x>1 \end{cases} a=1\)
For the following exercises, evaluate each limit using algebraic techniques.
\(\lim \limits_{x \to −5}(\frac{\frac{1}{5}+\frac{1}{x}}{10+2x})\)
\(−\frac{1}{50}\)
\(\lim \limits_{h \to 0} (\frac{\sqrt{h^2+25}−5}{h^2})\)
\(\lim \limits_{h \to 0} (\frac{1}{h}−\frac{1}{h^2+h})\)
1
For the following exercises, determine whether or not the given function \(f\) is continuous. If it is continuous, show why. If it is not continuous, state which conditions fail.
\(f(x)=\sqrt{x^2−4}\)
\(f(x)=\frac{x^3−4x^2−9x+36}{x^3−3x^2+2x−6}\)
removable discontinuity at \(x=3\)
For the following exercises, use the definition of a derivative to find the derivative of the given function at \(x=a\).
\(f(x)=\frac{3}{5+2x}\)
\(f(x)=\frac{3}{\sqrt{x}}\)
\(f'(x)=−\frac{3}{2a^{\frac{3}{2}}}\)
\(f(x)=2x^2+9x\)
discontinuous at –2,0, not differentiable at –2,0, 2.
For the following exercises, with the aid of a graphing utility, explain why the function is not differentiable everywhere on its domain. Specify the points where the function is not differentiable.
\(f(x)=| x−2 |−| x+2 |\)
\(f(x)=\frac{2}{1+e^{\frac{2}{x}}}\)
not differentiable at \(x=0\) (no limit)
For the following exercises, explain the notation in words when the height of a projectile in feet, \(s\), is a function of time t t in seconds after launch and is given by the function \(s(t)\).
\(s(0)\)
\(s(2)\)
the height of the projectile at \(t=2\) seconds
\(s'(2)\)
\(\frac{s(2)−s(1)}{2−1}\)
the average velocity from \(t=1\) to \(t=2\)
\(s(t)=0\)
For the following exercises, use technology to evaluate the limit.
\(\lim \limits_{x \to 0} \frac{\sin (x)}{3x}\)
\(\frac{1}{3}\)
\(\lim \limits_{x \to 0} \frac{\tan ^2 (x)}{2x}\)
\(\lim \limits_{x \to 0}\frac{\sin (x)(1−\cos (x))}{2x^2}\)
0
Evaluate the limit by hand.
\(\lim \limits_{x \to 1}f(x), \text{where } f(x)= \begin{cases} 4x−7 && x≠1 \\ x^2−4 &&x=1 \end{cases}\)
At what value(s) of \(x\) is the function below discontinuous?
\(f(x)= \begin{cases} 4x−7 && x≠1 \\ x^2−4 &&x=1 \end{cases}\)
For the following exercises, consider the function whose graph appears in Figure.
Find the average rate of change of the function from \(x=1\) to \(x=3\).
2
Find all values of \(x\) at which \(f'(x)=0\).
\(x=1\)
Find all values of \(x\) at which \(f'(x)\) does not exist.
Find an equation of the tangent line to the graph of \(f\) the indicated point: \(f(x)=3x^2−2x−6, x=−2\)
\(y=−14x−18\)
For the following exercises, use the function \(f(x)=x(1−x)^{\frac{2}{5}}\).
Graph the function \(f(x)=x(1−x)^{\frac{2}{5}}\) by entering \(f(x)=x((1−x)^2)^{\frac{1}{5}}\) and then by entering \(f(x)=x((1−x)^{\frac{1}{5}})^2\).
Explore the behavior of the graph of \(f(x)\) around \(x=1\) by graphing the function on the following domains, [0.9, 1.1], [0.99, 1.01], [0.999, 1.001], and [0.9999, 1.0001]. Use this information to determine whether the function appears to be differentiable at \(x=1\).
The graph is not differentiable at \(x=1\) (cusp).
For the following exercises, find the derivative of each of the functions using the definition: \(\lim \limits_{h \to 0} \frac{f(x+h)−f(x)}{h}\)
\(f(x)=2x−8\)
\(f(x)=4x^2−7\)
\(f′(x)=8x\)
\(f(x)=x−\frac{1}{2}x^2\)
\(f(x)=\frac{1}{x+2}\)
\(f'(x)=−\frac{1}{(2+x)^2}\)
\(f(x)=\frac{3}{x−1}\)
\(f(x)=−x^3+1\)
\(f′(x)=−3^x2\)
\(f(x)=x^2+x^3\)
\(f(x)=\sqrt{x−1}\)
\(f'(x)=\frac{1}{2\sqrt{x−1}}\)
Footnotes
- 1 www.csun.edu/science/health/d...tv&health.html Source provided.
Glossary
- average rate of change
- the slope of the line connecting the two points \((a,f(a))\) and \((a+h,f(a+h))\) on the curve of \(f(x)\); it is given by
\[\text{AROC}=\dfrac{f(a+h)−f(a)}{h}.\]
- derivative
- the slope of a function at a given point; denoted \(f′(a)\),at a point \(x=a\) it is \(f′(a)=\lim \limits_{h \to 0}\frac{f(a+h)−f(a)}{h}\),providing the limit exists.
- differentiable
- a function \(f(x)\) for which the derivative exists at \(x=a.\) In other words, if f′(a) f′(a) exists.
- instantaneous rate of change
- the slope of a function at a given point; at \(x=a\) it is given by \(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}\).
- instantaneous velocity
- the change in speed or direction at a given instant; a function \(s(t)\) represents the position of an object at time \(t\),and the instantaneous velocity or velocity of the object at time \(t=a\) is given by \(s′(a)=\lim \limits_{h \to 0}\frac{s(a+h)−s(a)}{h}\).
- secant line
- a line that intersects two points on a curve
- tangent line
- a line that intersects a curve at a single point


