11.2: The Law of Sines
- Page ID
- 80827
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Trigonometry literally means ‘measuring triangles’ and with Chapter 10 under our belts, we are more than prepared to do just that. The main goal of this section and the next is to develop theorems which allow us to ‘solve’ triangles – that is, find the length of each side of a triangle and the measure of each of its angles. In Sections 10.2, 10.3 and 10.6, we’ve had some experience solving right triangles. The following example reviews what we know.
Given a right triangle with a hypotenuse of length 7 units and one leg of length 4 units, find the length of the remaining side and the measures of the remaining angles. Express the angles in decimal degrees, rounded to the nearest hundreth of a degree.
Solution
For definitiveness, we label the triangle below.
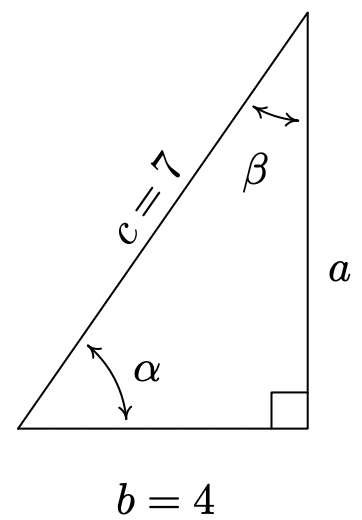
To find the length of the missing side \(a\), we use the Pythagorean Theorem to get \(a^{2}+4^{2}=7^{2}\) which then yields \(a=\sqrt{33}\) units. Now that all three sides of the triangle are known, there are several ways we can find \(\alpha\) using the inverse trigonometric functions. To decrease the chances of propagating error, however, we stick to using the data given to us in the problem. In this case, the lengths 4 and 7 were given, so we want to relate these to \(\alpha\). According to Theorem 10.4, \(\cos (\alpha)=\frac{4}{7}\). Since \(\alpha\) is an acute angle, \(\alpha=\arccos \left(\frac{4}{7}\right)\) radians. Converting to degrees, we find \(\alpha \approx 55.15^{\circ}\). Now that we have the measure of angle \(\alpha\), we could find the measure of angle \(\beta\) using the fact that \(\alpha\) and \(\beta\) are complements so \(\alpha+\beta=90^{\circ}\). Once again, we opt to use the data given to us in the problem. According to Theorem 10.4, we have that \(\sin (\beta)=\frac{4}{7}\) so \(\beta=\arcsin \left(\frac{4}{7}\right)\) radians and we have \(\beta \approx 34.85^{\circ}\).
A few remarks about Example 11.2.1 are in order. First, we adhere to the convention that a lower case Greek letter denotes an angle1 and the corresponding lowercase English letter represents the side2 opposite that angle. Thus, \(a\) is the side opposite \(\alpha, b\) is the side opposite \(\beta\) and \(c\) is the side opposite \(\gamma\). Taken together, the pairs \((\alpha, a)\), \((\beta, b)\) and \((\gamma, c)\) are called angle-side opposite pairs. Second, as mentioned earlier, we will strive to solve for quantities using the original data given in the problem whenever possible. While this is not always the easiest or fastest way to proceed, it minimizes the chances of propagated error.3 Third, since many of the applications which require solving triangles ‘in the wild’ rely on degree measure, we shall adopt this convention for the time being.4 The Pythagorean Theorem along with Theorems 10.4 and 10.10 allow us to easily handle any given right triangle problem, but what if the triangle isn’t a right triangle? In certain cases, we can use the Law of Sines to help.
Given a triangle with angle-side opposite pairs \((\alpha, a)\), \((\beta, b)\) and \((\gamma, c)\), the following ratios hold
\(\frac{\sin (\alpha)}{a}=\frac{\sin (\beta)}{b}=\frac{\sin (\gamma)}{c}\)
or, equivalently,
\(\frac{a}{\sin (\alpha)}=\frac{b}{\sin (\beta)}=\frac{c}{\sin (\gamma)}\)
The proof of the Law of Sines can be broken into three cases. For our first case, consider the triangle \(\triangle A B C\) below, all of whose angles are acute, with angle-side opposite pairs \((\alpha, a)\), \((\beta, b)\) and \((\gamma, c)\). If we drop an altitude from vertex \(B\), we divide the triangle into two right triangles: \(\triangle A B Q\) and \(\triangle B C Q\). If we call the length of the altitude \(h\) (for height), we get from Theorem 10.4 that \(\sin (\alpha)=\frac{h}{c}\) and \(\sin (\gamma)=\frac{h}{a}\) so that \(h=c \sin (\alpha)=a \sin (\gamma)\). After some rearrangement of the last equation, we get \(\frac{\sin (\alpha)}{a}=\frac{\sin (\gamma)}{c}\). If we drop an altitude from vertex \(A\), we can proceed as above using the triangles \(\triangle A B Q\) and \(\triangle A C Q\) to get \(\frac{\sin (\beta)}{b}=\frac{\sin (\gamma)}{c}\), completing the proof for this case.
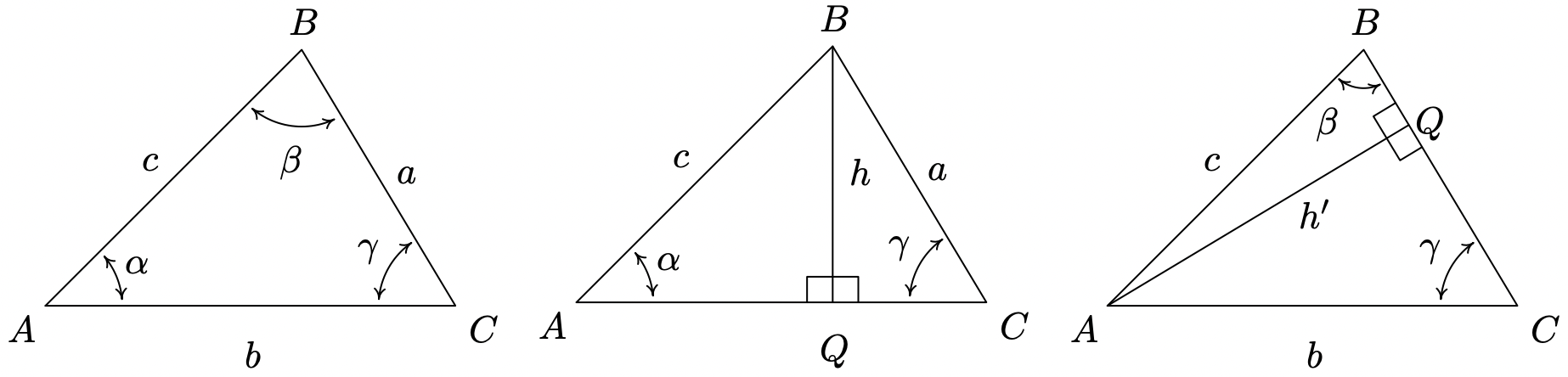
For our next case consider the triangle \(\triangle A B C\) below with obtuse angle \(\alpha\). Extending an altitude from vertex \(A\) gives two right triangles, as in the previous case: \(\triangle A B Q\) and \(\triangle A C Q\). Proceeding as before, we get \(h=b \sin (\gamma)\) and \(h=c \sin (\beta)\) so that \(\frac{\sin (\beta)}{b}=\frac{\sin (\gamma)}{c}\).

Dropping an altitude from vertex B also generates two right triangles, \(\triangle A B Q\) and \(\triangle B C Q\). We know that \(\sin \left(\alpha^{\prime}\right)=\frac{h^{\prime}}{c}\) so that \(h^{\prime}=c \sin \left(\alpha^{\prime}\right)\). Since \(\alpha^{\prime}=180^{\circ}-\alpha, \sin \left(\alpha^{\prime}\right)=\sin (\alpha)\), so in fact, we have \(h^{\prime}=c \sin (\alpha)\). Proceeding to \(\triangle B C Q\), we get \(\sin (\gamma)=\frac{h^{\prime}}{a} \text { so } h^{\prime}=a \sin (\gamma)\). Putting this together with the previous equation, we get \(\frac{\sin (\gamma)}{c}=\frac{\sin (\alpha)}{a}\), and we are finished with this case.
The remaining case is when \(\triangle A B C\) is a right triangle. In this case, the Law of Sines reduces to the formulas given in Theorem 10.4 and is left to the reader. In order to use the Law of Sines to solve a triangle, we need at least one angle-side opposite pair. The next example showcases some of the power, and the pitfalls, of the Law of Sines.
Solve the following triangles. Give exact answers and decimal approximations (rounded to hundredths) and sketch the triangle.
- \(\alpha=120^{\circ}, a=7 \text { units, } \beta=45^{\circ}\)
- \(\alpha=85^{\circ}, \beta=30^{\circ}, c=5.25 \text { units }\)
- \(\alpha=30^{\circ}, a=1 \text { units, } c=4 \text { units }\)
- \(\alpha=30^{\circ}, a=2 \text { units, } c=4 \text { units }\)
- \(\alpha=30^{\circ}, a=3 \text { units, } c=4 \text { units }\)
- \(\alpha=30^{\circ}, a=4 \text { units, } c=4 \text { units }\)
Solution
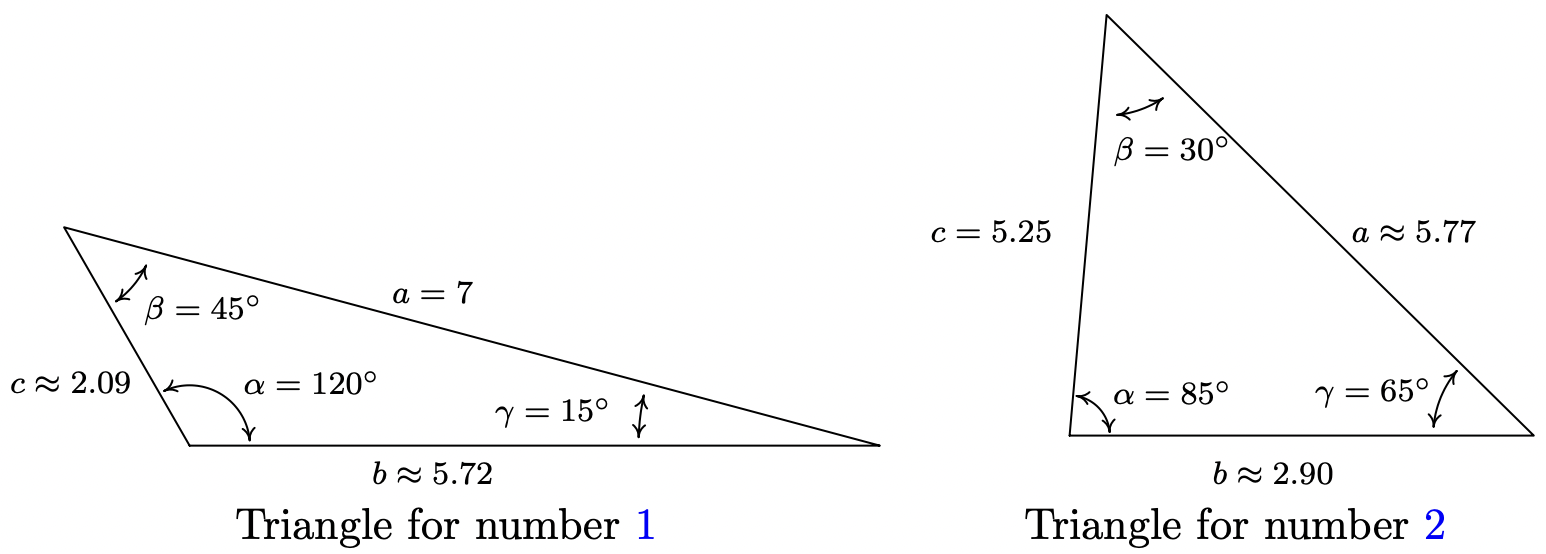
- Knowing an angle-side opposite pair, namely \(\alpha\) and \(a\), we may proceed in using the Law of Sines. Since \(\beta=45^{\circ}\), we use \(\frac{b}{\sin \left(45^{\circ}\right)}=\frac{7}{\sin \left(120^{\circ}\right)}\) so \(b=\frac{7 \sin \left(45^{\circ}\right)}{\sin \left(120^{\circ}\right)}=\frac{7 \sqrt{6}}{3} \approx 5.72\) units. Now that we have two angle-side pairs, it is time to find the third. To find \(\gamma\), we use the fact that the sum of the measures of the angles in a triangle is \(180^{\circ}\). Hence, \(\gamma=180^{\circ}-120^{\circ}-45^{\circ}=15^{\circ}\). To find \(c\), we have no choice but to used the derived value \(\gamma=15^{\circ}\), yet we can minimize the propagation of error here by using the given angle-side opposite pair \((\alpha, a)\). The Law of Sines gives us \(\frac{c}{\sin \left(15^{\circ}\right)}=\frac{7}{\sin \left(120^{\circ}\right)}\) so that \(c=\frac{7 \sin \left(15^{\circ}\right)}{\sin \left(120^{\circ}\right)} \approx 2.09\) units.5
- In this example, we are not immediately given an angle-side opposite pair, but as we have the measures of \(\alpha\) and \(\beta\), we can solve for \(\gamma\) since \(\gamma=180^{\circ}-85^{\circ}-30^{\circ}=65^{\circ}\). As in the previous example, we are forced to use a derived value in our computations since the only angle-side pair available is \((\gamma, c)\). The Law of Sines gives \(\frac{a}{\sin \left(85^{\circ}\right)}=\frac{5.25}{\sin \left(65^{\circ}\right)}\). After the usual rearrangement, we get \(a=\frac{5.25 \sin \left(85^{\circ}\right)}{\sin \left(65^{\circ}\right)} \approx 5.77\) units. To find \(b\) we use the angle-side pair \((\gamma, c)\) which yields \(\frac{b}{\sin \left(30^{\circ}\right)}=\frac{5.25}{\sin \left(65^{\circ}\right)}\) hence \(b=\frac{5.25 \sin \left(30^{\circ}\right)}{\sin \left(65^{\circ}\right)} \approx 2.90\) units.
- Since we are given \((\alpha, a)\) and \(c\), we use the Law of Sines to find the measure of \(\gamma\). We start with \(\frac{\sin (\gamma)}{4}=\frac{\sin \left(30^{\circ}\right)}{1}\) and get \(\sin (\gamma)=4 \sin \left(30^{\circ}\right)=2\). Since the range of the sine function is [−1, 1], there is no real number with \(\sin (\gamma)=2\). Geometrically, we see that side \(a\) is just too short to make a triangle. The next three examples keep the same values for the measure of \(\alpha\) and the length of \(c\) while varying the length of \(a\). We will discuss this case in more detail after we see what happens in those examples.
- In this case, we have the measure of \(\alpha=30^{\circ}\), \(a = 2\) and \(c = 4\). Using the Law of Sines, we get \(\frac{\sin (\gamma)}{4}=\frac{\sin \left(30^{\circ}\right)}{2}\) so \(\sin (\gamma)=2 \sin \left(30^{\circ}\right)=1\). Now \(\gamma\) is an angle in a triangle which also contains \(\alpha=30^{\circ}\). This means that \(\gamma\) must measure between \(0^{\circ}\) and \(150^{\circ}\) in order to fit inside the triangle with \(\alpha\). The only angle that satisfies this requirement and has \(\sin (\gamma)=1\) is \(\gamma=90^{\circ}\). In other words, we have a right triangle. We find the measure of \(\beta\) to be \(\beta=180^{\circ}-30^{\circ}-90^{\circ}=60^{\circ}\) and then determine \(b\) using the Law of Sines. We find \(b=\frac{2 \sin \left(60^{\circ}\right)}{\sin \left(30^{\circ}\right)}=2 \sqrt{3} \approx 3.46\) units. In this case, the side \(a\) is precisely long enough to form a unique right triangle.
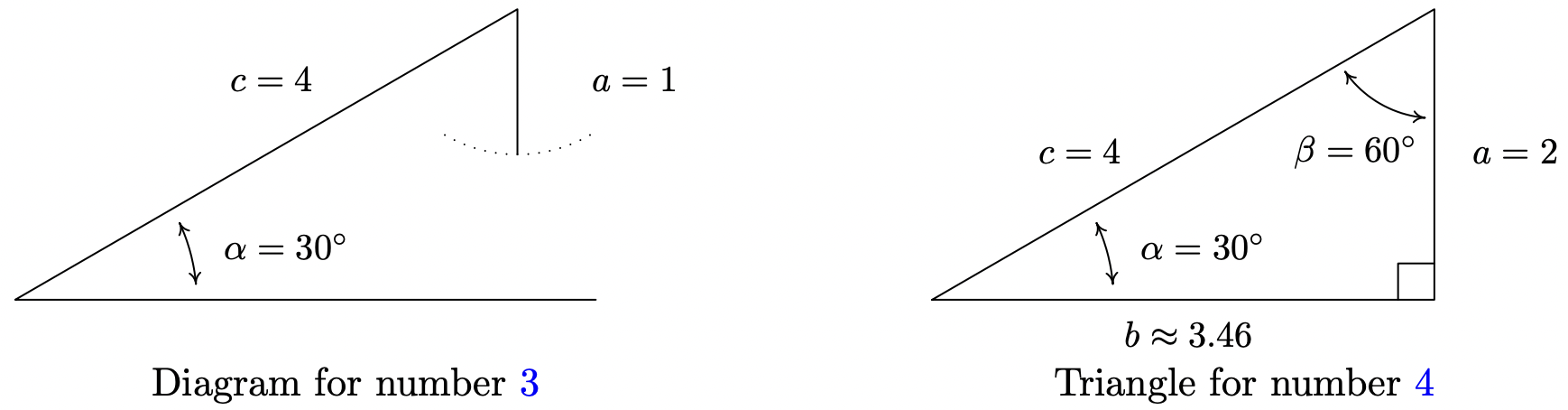
- Proceeding as we have in the previous two examples, we use the Law of Sines to find \(\gamma\). In this case, we have \(\frac{\sin (\gamma)}{4}=\frac{\sin \left(30^{\circ}\right)}{3}\) or \(\sin (\gamma)=\frac{4 \sin \left(30^{\circ}\right)}{3}=\frac{2}{3}\). Since \(\gamma\) lies in a triangle with \(\alpha=30^{\circ}\), we must have that \(0^{\circ}<\gamma<150^{\circ}\). There are two angles \(\gamma\) that fall in this range and have \(\sin (\gamma)=\frac{2}{3}\): \(\gamma=\arcsin \left(\frac{2}{3}\right) \text { radians } \approx 41.81^{\circ}\) and \(\gamma=\pi-\arcsin \left(\frac{2}{3}\right) \text { radians } \approx 138.19^{\circ}\). At this point, we pause to see if it makes sense that we actually have two viable cases to consider. As we have discussed, both candidates for \(\gamma\) are ‘compatible’ with the given angle-side pair \((\alpha, a)=\left(30^{\circ}, 3\right)\) in that both choices for \(\gamma\) can fit in a triangle with \(\alpha\) and both have a sine of \(\frac{2}{3}\). The only other given piece of information is that \(c = 4\) units. Since \(c>a\), it must be true that \(\gamma\), which is opposite \(c\), has greater measure than \(\alpha\) which is opposite \(a\). In both case, \(\gamma>\alpha\), which is opposite \(c\), has greater measure than \(\alpha\) which is opposite \(a\). In both case, \(\gamma>\alpha\), so both candidates for \(\gamma\) are compatible with this last piece of given information as well. Thus have two triangles on our hands. In the case \(\gamma=\arcsin \left(\frac{2}{3}\right) \text { radians } \approx 41.81^{\circ}\), we find6 \(\beta \approx 180^{\circ}-30^{\circ}-41.81^{\circ}=108.19^{\circ}\). Using the Law of Sines with the angle-side opposite pair \((\alpha, a)\) and \(\beta\), we find \(b \approx \frac{3 \sin \left(108.19^{\circ}\right)}{\sin \left(30^{\circ}\right)} \approx 5.70\) units. In the case \(\gamma=\pi-\arcsin \left(\frac{2}{3}\right)\) radians \(\approx 138.19^{\circ}\), we repeat the exact same steps and find \(\beta \approx 11.81^{\circ}\) and \(b \approx 1.23\) units.7 Both triangles are drawn below.
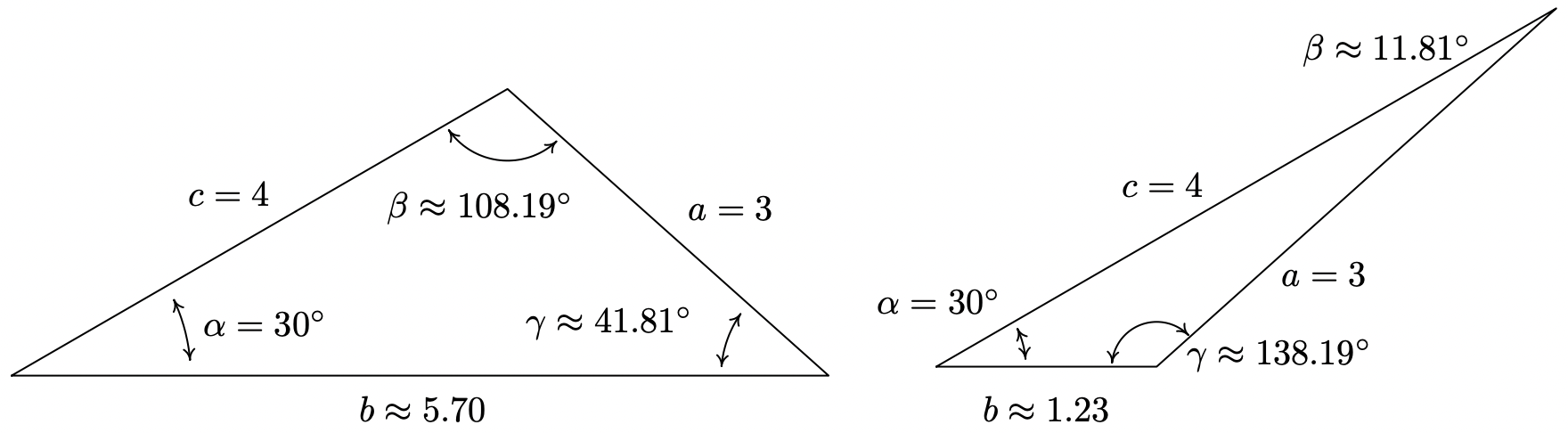
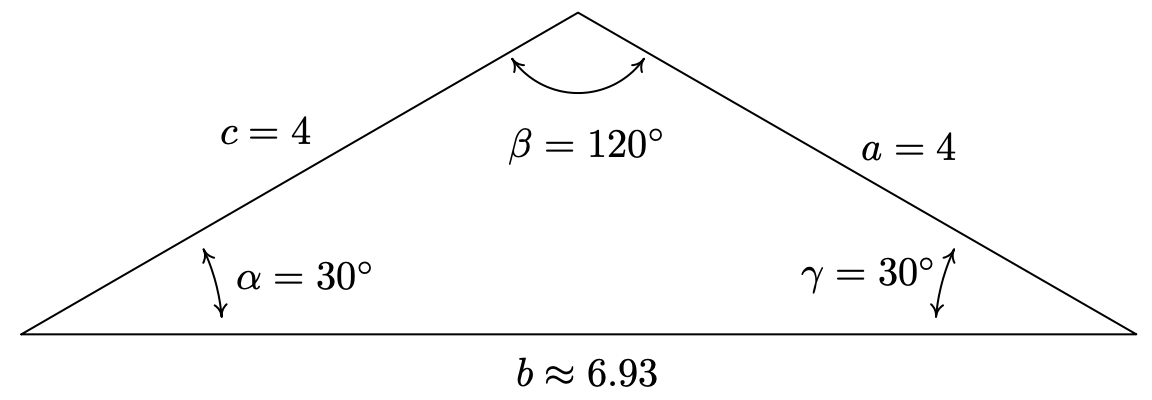
- For this last problem, we repeat the usual Law of Sines routine to find \(\frac{\sin (\gamma)}{4}=\frac{\sin \left(30^{\circ}\right)}{4}\) so that \(\sin (\gamma)=\frac{1}{2}\). Since \(\gamma\) must inhabit a triangle \(\alpha=30^{\circ}\), we must have \(0^{\circ}<\gamma<150^{\circ}\). Since the measure of \(\gamma\) must be strictly less than \(150^{\circ}\), there is just one angle which satisfies both required conditions, namely \(\gamma=30^{\circ}\). So \(\beta=180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}\) and, using the Law of Sines one last time, \(b=\frac{4 \sin \left(120^{\circ}\right)}{\sin \left(30^{\circ}\right)}=4 \sqrt{3} \approx 6.93\) units.
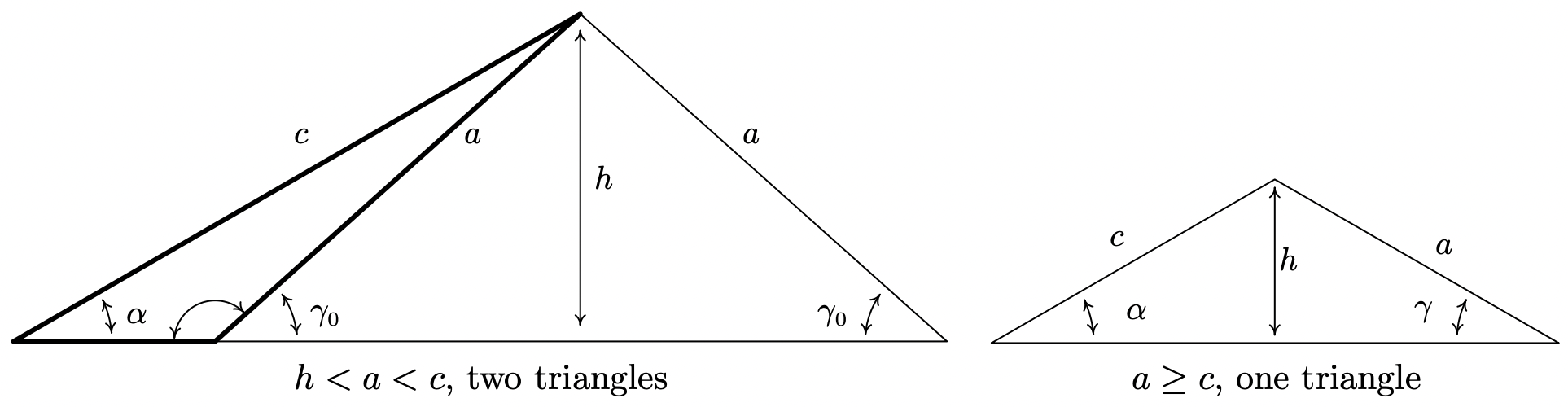
Some remarks about Example 11.2.2 are in order. We first note that if we are given the measures of two of the angles in a triangle, say \(\alpha\) and \(\beta\), the measure of the third angle \(\gamma\) uniquely determined using the equation \(\gamma=180^{\circ}-\alpha-\beta\). Knowing the measures of all three angles of a triangle completely determines its shape. If in addition we are given the length of one of the sides of the triangle, we can then use the Law of Sines to find the lengths of the remaining two sides to determine the size of the triangle. Such is the case in numbers 1 and 2 above. In number 1, the given side is adjacent to just one of the angles – this is called the ‘Angle-Angle-Side’ (AAS) case.8 In number 2, the given side is adjacent to both angles which means we are in the so-called ‘Angle-Side-Angle’ (ASA) case. If, on the other hand, we are given the measure of just one of the angles in the triangle along with the length of two sides, only one of which is adjacent to the given angle, we are in the ‘Angle-Side-Side’ (ASS) case.9 In number 3, the length of the one given side \(a\) was too short to even form a triangle; in number 4, the length of a was just long enough to form a right triangle; in 5, \(a\) was long enough, but not too long, so that two triangles were possible; and in number 6, side \(a\) was long enough to form a triangle but too long to swing back and form two. These four cases exemplify all of the possibilities in the Angle-Side-Side case which are summarized in the following theorem.
Suppose \((\alpha, a)\) and \((\gamma, c)\) are intended to be angle-side pairs in a triangle where \(\alpha\), \(a\) and \(c\) are given. Let \(h=c \sin (\alpha)\).
- If \(a<h\), then no triangle exists which satisfies the given criteria.
- If \(a=h\), then \(\gamma=90^{\circ}\) so exactly one (right) triangle exists which satisfies the criteria.
- If \(h<a<c\), then two distinct triangles exist which satisfy the given criteria.
- If \(a \geq c\), then \(\gamma\) is acute and exactly one triangle exists which satisfies the given criteria
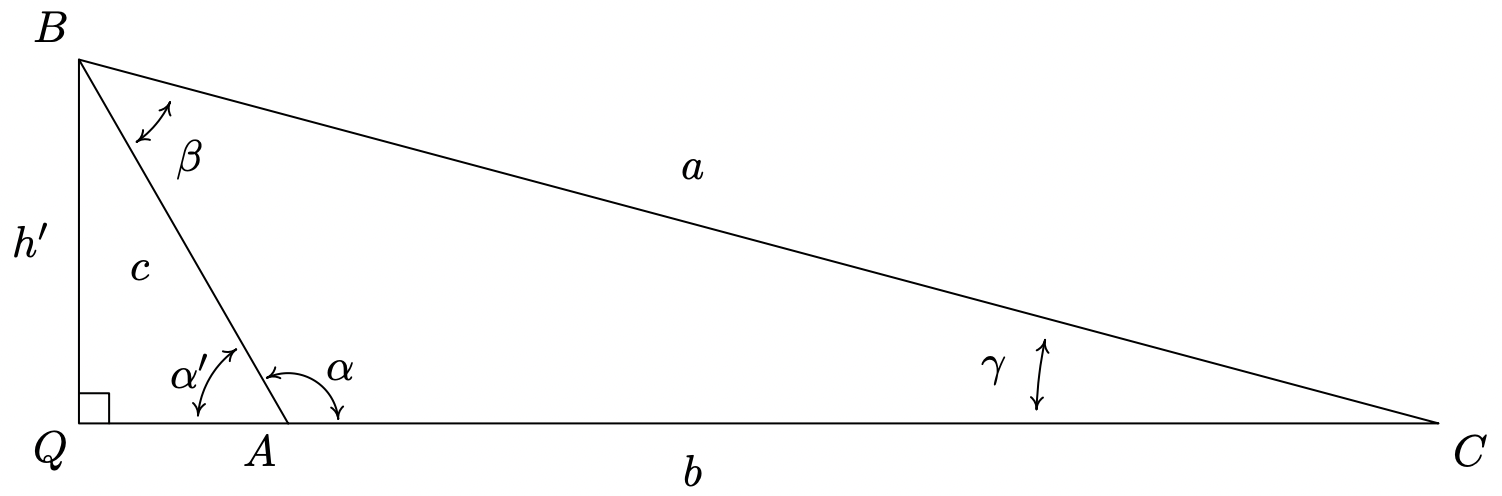
Theorem 11.3 is proved on a case-by-case basis. If \(a<h\), then \(a<c \sin (\alpha)\). If a triangle were to exist, the Law of Sines would have \(\frac{\sin (\gamma)}{c}=\frac{\sin (\alpha)}{a}\) so that \(\sin (\gamma)=\frac{c \sin (\alpha)}{a}>\frac{a}{a}=1\), which is impossible. In the figure below, we see geometrically why this is the case.
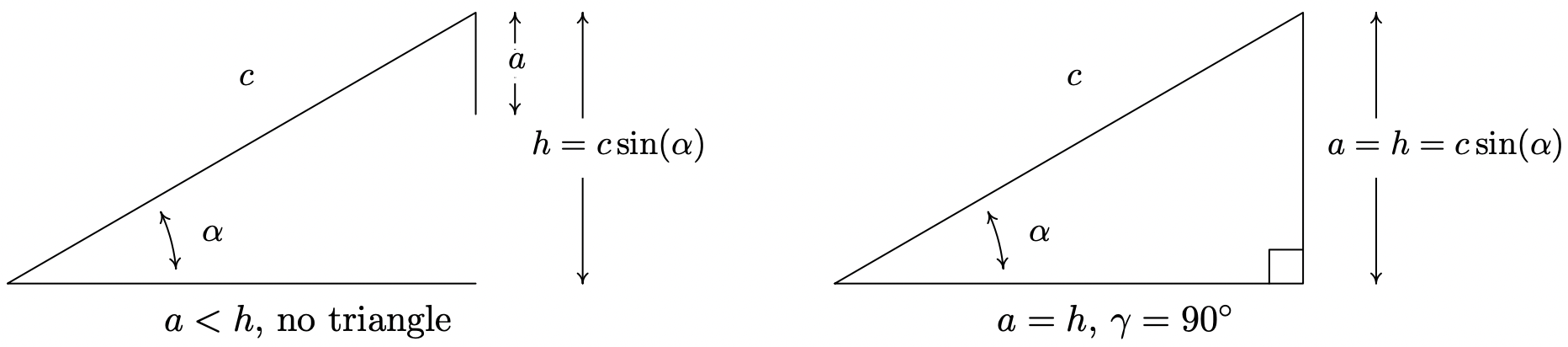
Simply put, if \(a<h\) the side \(a\) is too short to connect to form a triangle. This means if \(a \geq h\), we are always guaranteed to have at least one triangle, and the remaining parts of the theorem tell us what kind and how many triangles to expect in each case. If \(a = h\), then \(a=c \sin (\alpha)\) and the Law of Sines gives \(\frac{\sin (\alpha)}{a}=\frac{\sin (\gamma)}{c}\) so that \(\sin (\gamma)=\frac{c \sin (\alpha)}{a}=\frac{a}{a}=1\). Here, \(\gamma=90^{\circ}\) as required. Moving along, now suppose \(h<a<c\). As before, the Law of Sines10 gives \(\sin (\gamma)=\frac{c \sin (\alpha)}{a}\). Since \(h<a\), \(c \sin (\alpha)<a\) or \(\frac{c \sin (\alpha)}{a}<1\) which means there are two solutions to \(\sin (\gamma)=\frac{c \sin (\alpha)}{a}\): an acute angle which we’ll call \(\gamma_{0}\), and its supplement, \(180^{\circ}-\gamma_{0}\). We need to argue that each of these angles ‘fit’ into a triangle with \(\alpha\). Since \((\alpha, a)\) and \(\left(\gamma_{0}, c\right)\) are angle-side opposite pairs, the assumption \(c>a\) a in this case gives us \(\gamma_{0}>\alpha\). Since \(\gamma_{0}\) is acute, we must have that \(\alpha\) is acute as well. This means one triangle can contain both \(\alpha\) and \(\gamma_{0}\), giving us one of the triangles promised in the theorem. If we manipulate the inequality \(\gamma_{0}>\alpha\) a bit, we have \(180^{\circ}-\gamma_{0}<180^{\circ}-\alpha\) which gives \(\left(180^{\circ}-\gamma_{0}\right)+\alpha<180^{\circ}\). This proves a triangle can contain both of the angles \(\alpha\) and \(\left(180^{\circ}-\gamma_{0}\right)\), giving us the second triangle predicted in the theorem. To prove the last case in the theorem, we assume \(a \geq c\). Then \(\alpha \geq \gamma\), which forces \(\gamma\) to be an acute angle. Hence, we get only one triangle in this case, completing the proof.
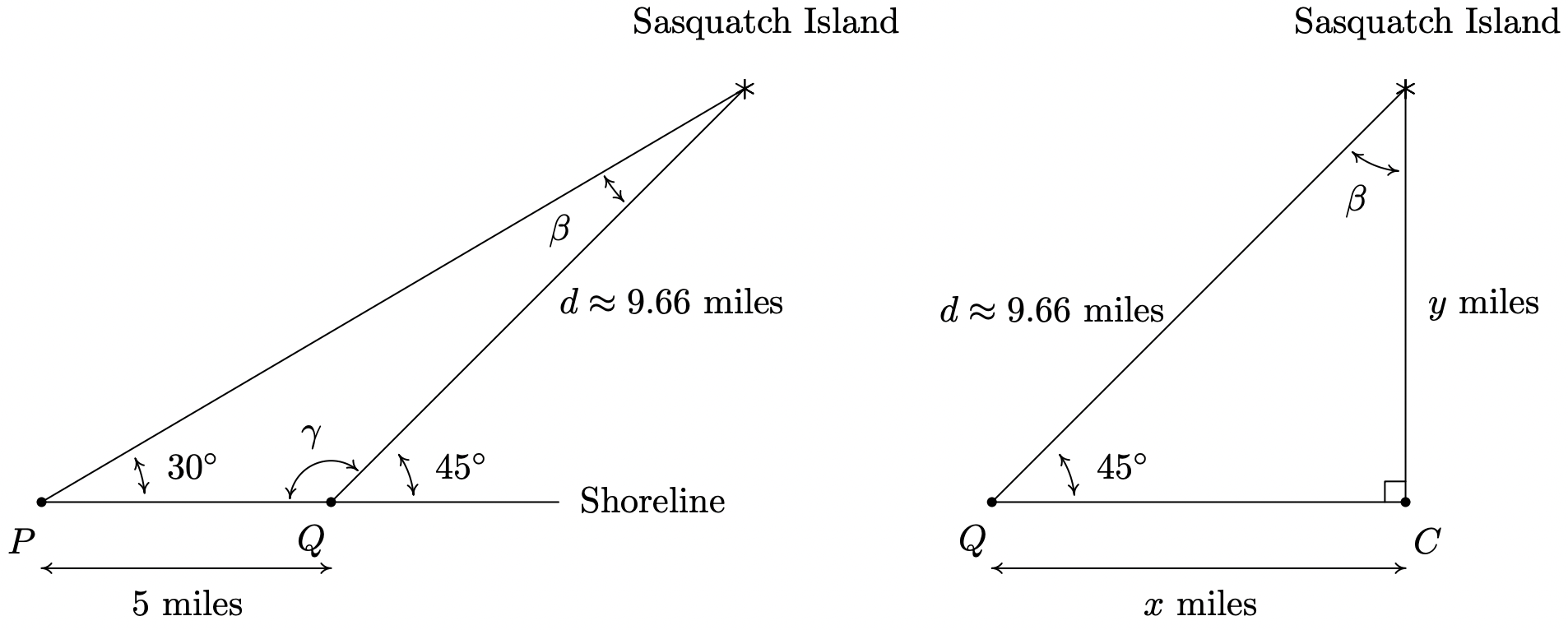
Sasquatch Island lies off the coast of Ippizuti Lake. Two sightings, taken 5 miles apart, are made to the island. The angle between the shore and the island at the first observation point is \(30^{\circ}\) and at the second point the angle is \(45^{\circ}\). Assuming a straight coastline, find the distance from the second observation point to the island. What point on the shore is closest to the island? How far is the island from this point?
Solution
We sketch the problem below with the first observation point labeled as \(P\) and the second as \(Q\). In order to use the Law of Sines to find the distance \(d\) from \(Q\) to the island, we first need to find the measure of \(\beta\) which is the angle opposite the side of length 5 miles. To that end, we note that the angles \(\gamma\) and \(45^{\circ}\) are supplemental, so that \(\gamma=180^{\circ}-45^{\circ}=135^{\circ}\). We can now find \(\beta=180^{\circ}-30^{\circ}-\gamma=180^{\circ}-30^{\circ}-135^{\circ}=15^{\circ}\). By the Law of Sines, we have \(\frac{d}{\sin \left(30^{\circ}\right)}=\frac{5}{\sin \left(15^{\circ}\right)}\) which gives \(d=\frac{5 \sin \left(30^{\circ}\right)}{\sin \left(15^{\circ}\right)} \approx 9.66\) miles. Next, to find the point on the coast closest to the island, which we’ve labeled as \(C\), we need to find the perpendicular distance from the island to the coast.11
Let \(x\) denote the distance from the second observation point \(Q\) to the point \(C\) and let \(y\) denote the distance from \(C\) to the island. Using Theorem 10.4, we get \(\sin \left(45^{\circ}\right)=\frac{y}{d}\). After some rearranging, we find \(y=d \sin \left(45^{\circ}\right) \approx 9.66\left(\frac{\sqrt{2}}{2}\right) \approx 6.83\) miles. Hence, the island is approximately 6.83 miles from the coast. To find the distance from \(Q\) to \(C\), we note that \(\beta=180^{\circ}-90^{\circ}-45^{\circ}=45^{\circ}\) so by symmetry,12 we get \(x=y \approx 6.83\) miles. Hence, the point on the shore closest to the island is approximately 6.83 miles down the coast from the second observation point.
We close this section with a new formula to compute the area enclosed by a triangle. Its proof uses the same cases and diagrams as the proof of the Law of Sines and is left as an exercise.
Suppose \((\alpha, a),(\beta, b) \text { and }(\gamma, c)\) are the angle-side opposite pairs of a triangle. Then the area \(A\) enclosed by the triangle is given by
\(A=\frac{1}{2} b c \sin (\alpha)=\frac{1}{2} a c \sin (\beta)=\frac{1}{2} a b \sin (\gamma)\)
Find the area of the triangle in Example 11.2.2 number 1.
Solution
From our work in Example 11.2.2 number 1, we have all three angles and all three sides to work with. However, to minimize propagated error, we choose \(A=\frac{1}{2} a c \sin (\beta)\) from Theorem 11.4 because it uses the most pieces of given information. We are given \(a=7\) and \(\beta=45^{\circ}\), and we calculated \(c=\frac{7 \sin \left(15^{\circ}\right)}{\sin \left(120^{\circ}\right)}\). Using these values, we find \(A=\frac{1}{2}(7)\left(\frac{7 \sin \left(15^{\circ}\right)}{\sin \left(120^{\circ}\right)}\right) \sin \left(45^{\circ}\right)=\approx 5.18\) square units. The reader is encouraged to check this answer against the results obtained using the other formulas in Theorem 11.4.
11.2.1 Exercises
In Exercises 1 - 20, solve for the remaining side(s) and angle(s) if possible. As in the text, \((\alpha, a)\), \((\beta, b)\) and \((\gamma, c)\) are angle-side opposite pairs.
- \(\alpha=13^{\circ}, \beta=17^{\circ}, a=5\)
- \(\alpha=73.2^{\circ}, \beta=54.1^{\circ}, a=117\)
- \(\alpha=95^{\circ}, \beta=85^{\circ}, a=33.33\)
- \(\alpha=95^{\circ}, \beta=62^{\circ}, a=33.33\)
- \(\alpha=117^{\circ}, a=35, b=42\)
- \(\alpha=117^{\circ}, a=45, b=42\)
- \(\alpha=68.7^{\circ}, a=88, b=92\)
- \(\alpha=42^{\circ}, a=17, b=23.5\)
- \(\alpha=68.7^{\circ}, a=70, b=90\)
- \(\alpha=30^{\circ}, a=7, b=14\)
- \(\alpha=42^{\circ}, a=39, b=23.5\)
- \(\gamma=53^{\circ}, \alpha=53^{\circ}, c=28.01\)
- \(\alpha=6^{\circ}, a=57, b=100\)
- \(\gamma=74.6^{\circ}, c=3, a=3.05\)
- \(\beta=102^{\circ}, b=16.75, c=13\)
- \(\beta=102^{\circ}, b=16.75, c=18\)
- \(\beta=102^{\circ}, \gamma=35^{\circ}, b=16.75\)
- \(\beta=29.13^{\circ}, \gamma=83.95^{\circ}, b=314.15\)
- \(\gamma=120^{\circ}, \beta=61^{\circ}, c=4\)
- \(\alpha=50^{\circ}, a=25, b=12.5\)
- Find the area of the triangles given in Exercises 1, 12 and 20 above.
(Another Classic Application: Grade of a Road) The grade of a road is much like the pitch of a roof (See Example 10.6.6) in that it expresses the ratio of rise/run. In the case of a road, this ratio is always positive because it is measured going uphill and it is usually given as a percentage. For example, a road which rises 7 feet for every 100 feet of (horizontal) forward progress is said to have a 7% grade. However, if we want to apply any Trigonometry to a story problem involving roads going uphill or downhill, we need to view the grade as an angle with respect to the horizontal. In Exercises 22 - 24, we first have you change road grades into angles and then use the Law of Sines in an application.
- Using a right triangle with a horizontal leg of length 100 and vertical leg with length 7, show that a \(7 \%\) grade means that the road (hypotenuse) makes about a \(4^{\circ}\) angle with the horizontal. (It will not be exactly \(4^{\circ}\), but it’s pretty close.)
- What grade is given by a \(9.65^{\circ}\) angle made by the road and the horizontal?13
- Along a long, straight stretch of mountain road with a 7% grade, you see a tall tree standing perfectly plumb alongside the road.14 From a point 500 feet downhill from the tree, the angle of inclination from the road to the top of the tree is \(6^{\circ}\). Use the Law of Sines to find the height of the tree. (Hint: First show that the tree makes a \(94^{\circ}\) angle with the road.)
(Another Classic Application: Bearings) In the next several exercises we introduce and work with the navigation tool known as bearings. Simply put, a bearing is the direction you are heading according to a compass. The classic nomenclature for bearings, however, is not given as an angle in standard position, so we must first understand the notation. A bearing is given as an acute angle of rotation (to the east or to the west) away from the north-south (up and down) line of a compass rose. For example, \(\mathrm{N} 40^{\circ} \mathrm{E}\) (read "\(40^{\circ}\) east of north”) is a bearing which is rotated clockwise \(40^{\circ}\) from due north. If we imagine standing at the origin in the Cartesian Plane, this bearing would have us heading into Quadrant I along the terminal side of \(\theta=50^{\circ}\). Similarly, \(\mathrm{S} 50^{\circ} \mathrm{W}\) would point into Quadrant III along the terminal side of \(\theta=220^{\circ}\) because we started out pointing due south (along \(\theta=270^{\circ}\)) and rotated clockwise \(50^{\circ}\) back to \(220^{\circ}\). Counter-clockwise rotations would be found in the bearings \(\mathrm{N} 60^{\circ} \mathrm{W}\) (which is on the terminal side of \(\theta=150^{\circ}\)) and \(\mathrm{S} 27^{\circ} \mathrm{E}\) (which lies along the terminal side of \(\theta=297^{\circ}\)). These four bearings are drawn in the plane below.
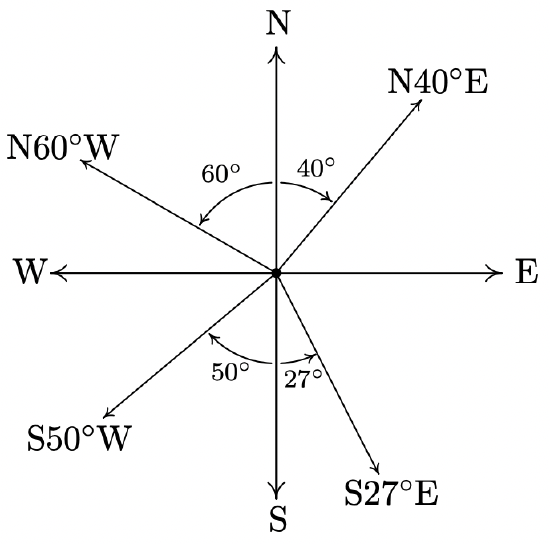
The cardinal directions north, south, east and west are usually not given as bearings in the fashion described above, but rather, one just refers to them as ‘due north’, ‘due south’, ‘due east’ and ‘due west’, respectively, and it is assumed that you know which quadrantal angle goes with each cardinal direction. (Hint: Look at the diagram above.)
- Find the angle \(\theta\) in standard position with \(0^{\circ} \leq \theta<360^{\circ}\) which corresponds to each of the bearings given below.
- due west
- \(\mathrm{S} 83^{\circ} \mathrm{E}\)
- \(\mathrm{N} 5.5^{\circ} \mathrm{E}\)
- due south
- \(\mathrm{N} 31.25^{\circ} \mathrm{W}\)
- \(\mathrm{S}{72}^{\circ} 41^{\prime} 12^{\prime \prime} \mathrm{W}\)15
- \(\mathrm{N} 45^{\circ} \mathrm{E}\)
- \(\mathrm{S}{45}{ }^{\circ} \mathrm{W}\)
- The Colonel spots a campfire at a of bearing \(\mathrm{N} 42^{\circ} \mathrm{E}\) from his current position. Sarge, who is positioned 3000 feet due east of the Colonel, reckons the bearing to the fire to be \(\mathrm{N} 20^{\circ} \mathrm{W}\) from his current position. Determine the distance from the campfire to each man, rounded to the nearest foot.
- A hiker starts walking due west from Sasquatch Point and gets to the Chupacabra Trailhead before she realizes that she hasn’t reset her pedometer. From the Chupacabra Trailhead she hikes for 5 miles along a bearing of \(\mathrm{N} 53^{\circ} \mathrm{W}\) which brings her to the Muffin Ridge Observatory. From there, she knows a bearing of \(\mathrm{S}6 5^{\circ} \mathrm{E}\) will take her straight back to Sasquatch Point. How far will she have to walk to get from the Muffin Ridge Observatory to Sasquach Point? What is the distance between Sasquatch Point and the Chupacabra Trailhead?
- The captain of the SS Bigfoot sees a signal flare at a bearing of \(\mathrm{N} 15^{\circ} \mathrm{E}\) from her current location. From his position, the captain of the HMS Sasquatch finds the signal flare to be at a bearing of \(\mathrm{N} 75^{\circ} \mathrm{W}\). If the SS Bigfoot is 5 miles from the HMS Sasquatch and the bearing from the SS Bigfoot to the HMS Sasquatch is \(\mathrm{N} 50^{\circ} \mathrm{E}\), find the distances from the flare to each vessel, rounded to the nearest tenth of a mile.
- Carl spies a potential Sasquatch nest at a bearing of \(\mathrm{N} 10^{\circ} \mathrm{E}\) and radios Jeff, who is at a bearing of \(\mathrm{N} 50^{\circ} \mathrm{E}\) from Carl’s position. From Jeff’s position, the nest is at a bearing of \(\mathrm{S} 70^{\circ} \mathrm{W}\). If Jeff and Carl are 500 feet apart, how far is Jeff from the Sasquatch nest? Round your answer to the nearest foot.
- A hiker determines the bearing to a lodge from her current position is \(\mathrm{S} 40^{\circ} \mathrm{W}\). She proceeds to hike 2 miles at a bearing of \(\mathrm{S} 20^{\circ} \mathrm{E}\) at which point she determines the bearing to the lodge is \(\mathrm{S}{75}{ }^{\circ} \mathrm{W}\). How far is she from the lodge at this point? Round your answer to the nearest hundredth of a mile.
- A watchtower spots a ship off shore at a bearing of \(\mathrm{N} 70^{\circ} \mathrm{E}\). A second tower, which is 50 miles from the first at a bearing of \(\mathrm{S} 80^{\circ} \mathrm{E}\) from the first tower, determines the bearing to the ship to be \(\mathrm{N} 25^{\circ} \mathrm{W}\). How far is the boat from the second tower? Round your answer to the nearest tenth of a mile.
- Skippy and Sally decide to hunt UFOs. One night, they position themselves 2 miles apart on an abandoned stretch of desert runway. An hour into their investigation, Skippy spies a UFO hovering over a spot on the runway directly between him and Sally. He records the angle of inclination from the ground to the craft to be \(75^{\circ}\) and radios Sally immediately to find the angle of inclination from her position to the craft is \(50^{\circ}\). How high off the ground is the UFO at this point? Round your answer to the nearest foot. (Recall: 1 mile is 5280 feet.)
- The angle of depression from an observer in an apartment complex to a gargoyle on the building next door is \(55^{\circ}\). From a point five stories below the original observer, the angle of inclination to the gargoyle is \(20^{\circ}\). Find the distance from each observer to the gargoyle and the distance from the gargoyle to the apartment complex. Round your answers to the nearest foot. (Use the rule of thumb that one story of a building is 9 feet.)
- Prove that the Law of Sines holds when \(\triangle A B C\) is a right triangle.
- Discuss with your classmates why knowing only the three angles of a triangle is not enough to determine any of the sides.
- Discuss with your classmates why the Law of Sines cannot be used to find the angles in the triangle when only the three sides are given. Also discuss what happens if only two sides and the angle between them are given. (Said another way, explain why the Law of Sines cannot be used in the SSS and SAS cases.)
- Given \(\alpha=30^{\circ}\) and \(b = 10\), choose four different values for \(a\) so that
- the information yields no triangle
- the information yields exactly one right triangle
- the information yields two distinct triangles
- the information yields exactly one obtuse triangle
Explain why you cannot choose \(a\) in such a way as to have \(\alpha=30^{\circ}, b=10\) and your choice of \(a\) yield only one triangle where that unique triangle has three acute angles.
- Use the cases and diagrams in the proof of the Law of Sines (Theorem 11.2) to prove the area formulas given in Theorem 11.4. Why do those formulas yield square units when four quantities are being multiplied together?
11.2.2 Answers
- \(\begin{array}{lll}
\alpha=13^{\circ} & \beta=17^{\circ} & \gamma=150^{\circ} \\
a=5 & b \approx 6.50 & c \approx 11.11
\end{array}\) - \(\begin{array}{lll}
\alpha=73.2^{\circ} & \beta=54.1^{\circ} & \gamma=52.7^{\circ} \\
a=117 & b \approx 99.00 & c \approx 97.22
\end{array}\) - Information does not produce a triangle
- \( \begin{array}{lll}
\alpha=95^{\circ} & \beta=62^{\circ} & \gamma=23^{\circ} \\
a=33.33 & b \approx 29.54 & c \approx 13.07
\end{array}\) - Information does not produce a triangle
- \(\begin{array}{lll}
\alpha=117^{\circ} & \beta \approx 56.3^{\circ} & \gamma \approx 6.7^{\circ} \\
a=45 & b=42 & c \approx 5.89
\end{array}\) - \(\begin{array}{lll}
\alpha=68.7^{\circ} & \beta \approx 76.9^{\circ} & \gamma \approx 34.4^{\circ} \\
a=88 & b=92 & c \approx 53.36
\end{array}\) - \(\begin{array}{lll}
\alpha=42^{\circ} & \beta \approx 67.66^{\circ} & \gamma \approx 70.34^{\circ} \\
a=17 & b=23.5 & c \approx 23.93
\end{array}\) - Information does not produce a triangle
- \(\begin{array}{lll}
\alpha=30^{\circ} & \beta=90^{\circ} & \gamma=60^{\circ} \\
a=7 & b=14 & c=7 \sqrt{3}
\end{array}\) - \(\begin{array}{lll}
\alpha=42^{\circ} & \beta \approx 23.78^{\circ} & \gamma \approx 114.22^{\circ} \\
a=39 & b=23.5 & c \approx 53.15
\end{array}\) - \(\begin{array}{lll}
\alpha=53^{\circ} & \beta=74^{\circ} & \gamma=53^{\circ} \\
a=28.01 & b \approx 33.71 & c=28.01
\end{array}\) - \(\begin{array}{lll}
\alpha=6^{\circ} & \beta \approx 169.43^{\circ} & \gamma \approx 4.57^{\circ} \\
a=57 & b=100 & c \approx 43.45
\end{array}\) - \(\begin{array}{lll}
\alpha \approx 78.59^{\circ} & \beta \approx 26.81^{\circ} & \gamma=74.6^{\circ} \\
a=3.05 & b \approx 1.40 & c=3
\end{array}\) - \(\begin{array}{lll}
\alpha \approx 28.61^{\circ} & \beta=102^{\circ} & \gamma \approx 49.39^{\circ} \\
a \approx 8.20 & b=16.75 & c=13
\end{array}\) - Information does not produce a triangle
- \(\begin{array}{lll}
\alpha=43^{\circ} & \beta=102^{\circ} & \gamma=35^{\circ} \\
a \approx 11.68 & b=16.75 & c \approx 9.82
\end{array}\) - \(\begin{array}{lll}
\alpha=66.92^{\circ} & \beta=29.13^{\circ} & \gamma=83.95^{\circ} \\
a \approx 593.69 & b=314.15 & c \approx 641.75
\end{array}\) - Information does not produce a triangle
- \(\begin{array}{lll}
\alpha=50^{\circ} & \beta \approx 22.52^{\circ} & \gamma \approx 107.48^{\circ} \\
a=25 & b=12.5 & c \approx 31.13
\end{array}\) - The area of the triangle from Exercise 1 is about 8.1 square units.
The area of the triangle from Exercise 12 is about 377.1 square units.
The area of the triangle from Exercise 20 is about 149 square units.
- \(\arctan \left(\frac{7}{100}\right) \approx 0.699 \text { radians }\), which is equivalent to \(\(4.004^{\circ}\)
- About 17%
- About 53 feet
-
- \(\theta=180^{\circ}\)
- \(\theta=353^{\circ}\)
- \(\theta=84.5^{\circ}\)
- \(\theta=270^{\circ}\)
- \(\theta=121.25^{\circ}\)
- \(\theta=197^{\circ} 18^{\prime} 48^{\prime \prime}\)
- \(\theta=45^{\circ}\)
- \(\theta=225^{\circ}\)
- The Colonel is about 3193 feet from the campfire.
Sarge is about 2525 feet to the campfire.
- The distance from the Muffin Ridge Observatory to Sasquach Point is about 7.12 miles.
The distance from Sasquatch Point to the Chupacabra Trailhead is about 2.46 miles.
- The SS Bigfoot is about 4.1 miles from the flare.
The HMS Sasquatch is about 2.9 miles from the flare.
- Jeff is about 371 feet from the nest.
- She is about 3.02 miles from the lodge
- The boat is about 25.1 miles from the second tower.
- The UFO is hovering about 9539 feet above the ground.
- The gargoyle is about 44 feet from the observer on the upper floor.
The gargoyle is about 27 feet from the observer on the lower floor.
The gargoyle is about 25 feet from the other building.
Reference
1 as well as the measure of said angle
2 as well as the length of said side
3 Your Science teachers should thank us for this.
4 Don’t worry! Radians will be back before you know it!
5 The exact value of \(\sin \left(15^{\circ}\right)\) could be found using the difference identity for sine or a half-angle formula, but that becomes unnecessarily messy for the discussion at hand. Thus “exact” here means \(\frac{7 \sin \left(15^{\circ}\right)}{\sin \left(120^{\circ}\right)}\).
6 To find an exact expression for \(\beta\), we convert everything back to radians: \(\alpha=30^{\circ}=\frac{\pi}{6}\) radians, \(\gamma=\arcsin \left(\frac{2}{3}\right)\) radians and \(180^{\circ}=\pi\) radians. Hence, \(\beta=\pi-\frac{\pi}{6}-\arcsin \left(\frac{2}{3}\right)=\frac{5 \pi}{6}-\arcsin \left(\frac{2}{3}\right) \text { radians } \approx 108.19^{\circ}\).
7 An exact answer for \(\beta\) in this case is \(\beta=\arcsin \left(\frac{2}{3}\right)-\frac{\pi}{6} \text { radians } \approx 11.81^{\circ}\).
8 If this sounds familiar, it should. From high school Geometry, we know there are four congruence conditions for triangles: Angle-Angle-Side (AAS), Angle-Side-Angle (ASA), Side-Angle-Side (SAS) and Side-Side-Side (SSS). If we are given information about a triangle that meets one of these four criteria, then we are guaranteed that exactly one triangle exists which satisfies the given criteria.
9 In more reputable books, this is called the ‘Side-Side-Angle’ or SSA case.
10 Remember, we have already argued that a triangle exists in this case!
11 Do you see why \(C\) must lie to the right of \(Q\)?
12 Or by Theorem 10.4 again . . .
13 I have friends who live in Pacifica, CA and their road is actually this steep. It’s not a nice road to drive.
14 The word ‘plumb’ here means that the tree is perpendicular to the horizontal.
15 See Example 10.1.1 in Section 10.1 for a review of the DMS system.


