11.3: The Law of Cosines

In Section 11.2, we developed the Law of Sines (Theorem 11.2) to enable us to solve triangles in the ‘Angle-Angle-Side’ (AAS), the ‘Angle-Side-Angle’ (ASA) and the ambiguous ‘Angle-Side-Side’ (ASS) cases. In this section, we develop the Law of Cosines which handles solving triangles in the ‘Side-Angle-Side’ (SAS) and ‘Side-Side-Side’ (SSS) cases.¹ We state and prove the theorem below.

Theorem 11.5. Law of Cosines

Given a triangle with angle-side opposite pairs \((\alpha, a),(\beta, b)\) and \((\gamma, c)\), the following equations hold

\(a^{2}=b^{2}+c^{2}-2 b c \cos (\alpha) \quad b^{2}=a^{2}+c^{2}-2 a c \cos (\beta) \quad c^{2}=a^{2}+b^{2}-2 a b \cos (\gamma)\)

or, solving for the cosine in each equation, we have

\(\cos (\alpha)=\frac{b^{2}+c^{2}-a^{2}}{2 b c} \quad \cos (\beta)=\frac{a^{2}+c^{2}-b^{2}}{2 a c} \quad \cos (\gamma)=\frac{a^{2}+b^{2}-c^{2}}{2 a b}\)

To prove the theorem, we consider a generic triangle with the vertex of angle \(\alpha\) at the origin with side \(b\) positioned along the positive \(x\)-axis.

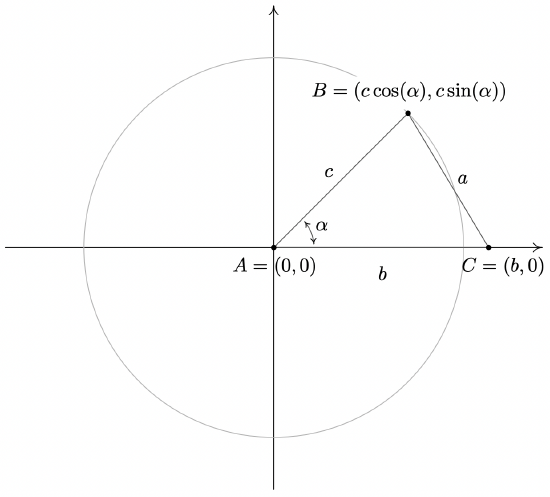
From this set-up, we immediately find that the coordinates of \(A\) and \(C\) are \(A(0, 0)\) and \(C(b, 0)\). From Theorem 10.3, we know that since the point \(B(x, y)\) lies on a circle of radius \(c\), the coordinates of \(B\) are \(B(x, y)=B(c \cos (\alpha), c \sin (\alpha))\). (This would be true even if \(\alpha\) were an obtuse or right angle so although we have drawn the case when α is acute, the following computations hold for any angle \(\alpha\) drawn in standard position where \(0<\alpha<180^{\circ}\).) We note that the distance between the points \(B\) and \(C\) is none other than the length of side \(a\). Using the distance formula, Equation 1.1, we get

\[\begin{aligned}
a &=\sqrt{(c \cos (\alpha)-b)^{2}+(c \sin (\alpha)-0)^{2}} \\
a^{2} &=\left(\sqrt{(c \cos (\alpha)-b)^{2}+c^{2} \sin ^{2}(\alpha)}\right)^{2} \\
a^{2} &=(c \cos (\alpha)-b)^{2}+c^{2} \sin ^{2}(\alpha) \\
a^{2} &=c^{2} \cos ^{2}(\alpha)-2 b c \cos (\alpha)+b^{2}+c^{2} \sin ^{2}(\alpha) \\
a^{2} &=c^{2}\left(\cos ^{2}(\alpha)+\sin ^{2}(\alpha)\right)+b^{2}-2 b c \cos (\alpha) \\
a^{2} &=c^{2}(1)+b^{2}-2 b c \cos (\alpha) \quad\quad\quad\quad\quad\quad\quad\quad \text{Since } \cos^2(\alpha) + \sin^2(\alpha)=1\\
a^{2} &=c^{2}+b^{2}-2 b c \cos (\alpha)
\end{aligned}\nonumber\]

The remaining formulas given in Theorem 11.5 can be shown by simply reorienting the triangle to place a different vertex at the origin. We leave these details to the reader. What’s important about \(a\) and \(\alpha\) in the above proof is that \((\alpha, a)\) is an angle-side opposite pair and \(b\) and \(c\) are the sides adjacent to \(\alpha\) – the same can be said of any other angle-side opposite pair in the triangle. Notice that the proof of the Law of Cosines relies on the distance formula which has its roots in the Pythagorean Theorem. That being said, the Law of Cosines can be thought of as a generalization of the Pythagorean Theorem. If we have a triangle in which \(\gamma=90^{\circ}\), then \(\cos (\gamma)=\cos \left(90^{\circ}\right)=0\) so we get the familiar relationship \(c^{2}=a^{2}+b^{2}\). What this means is that in the larger mathematical sense, the Law of Cosines and the Pythagorean Theorem amount to pretty much the same thing.²

Example 11.3.1

Solve the following triangles. Give exact answers and decimal approximations (rounded to hundredths) and sketch the triangle.

1. \(\beta=50^{\circ}, a=7 \text { units, } c=2 \text { units }\)
2. \(a=4 \text { units, } b=7 \text { units, } c=5 \text { units }\)

Solution

1. \(\cos (\alpha)=\frac{2-7 \cos \left(50^{\circ}\right)}{\sqrt{53-28 \cos \left(50^{\circ}\right)}}\)

   Since \(\alpha\) is an angle in a triangle, we know the radian measure of \(\alpha\) must lie between 0 and \(\pi\) radians. This matches the range of the arccosine function, so we have

   \(\alpha=\arccos \left(\frac{2-7 \cos \left(50^{\circ}\right)}{\sqrt{53-28 \cos \left(50^{\circ}\right)}}\right) \text { radians } \approx 114.99^{\circ}\)

   At this point, we could find \(\gamma\) using \(\gamma=180^{\circ}-\alpha-\beta \approx 180^{\circ}-114.99^{\circ}-50^{\circ}=15.01^{\circ}\), that is if we trust our approximation for \(\alpha\). To minimize propagation of error, however, we could use the Law of Cosines again,⁴ in this case using \(\cos (\gamma)=\frac{a^{2}+b^{2}-c^{2}}{2 a b}\). Plugging in \(a = 7\), \(b=\sqrt{53-28 \cos \left(50^{\circ}\right)}\) and \(c = 2\), we get \(\gamma=\arccos \left(\frac{7-2 \cos \left(50^{\circ}\right)}{\sqrt{53-28 \cos \left(50^{\circ}\right)}}\right) \text { radians } \approx 15.01^{\circ}\). We sketch the triangle below.

   

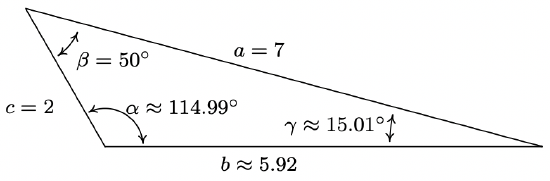
   As we mentioned earlier, once we’ve determined \(b\) it is possible to use the Law of Sines to find the remaining angles. Here, however, we must proceed with caution as we are in the ambiguous (ASS) case. It is advisable to first find the smallest of the unknown angles, since we are guaranteed it will be acute.⁵ In this case, we would find \(\gamma\) since the side opposite \(\gamma\) is smaller than the side opposite the other unknown angle, \(\alpha\). Using the angle-side opposite pair \((\beta, b)\), we get \(\frac{\sin (\gamma)}{2}=\frac{\sin \left(50^{\circ}\right)}{\sqrt{53-28 \cos \left(50^{\circ}\right)}}\). The usual calculations produces \(\gamma \approx 15.01^{\circ}\) and \(\alpha=180^{\circ}-\beta-\gamma \approx 180^{\circ}-50^{\circ}-15.01^{\circ}=114.99^{\circ}\).

2. Since all three sides and no angles are given, we are forced to use the Law of Cosines. Following our discussion in the previous problem, we find \(\beta\) first, since it is opposite the longest side, \(b\). We get \(\cos (\beta)=\frac{a^{2}+c^{2}-b^{2}}{2 a c}=-\frac{1}{5}\), so we get \(\beta=\arccos \left(-\frac{1}{5}\right) \text { radians } \approx 101.54^{\circ}\). As in the previous problem, now that we have obtained an angle-side opposite pair \((\beta, b)\), we could proceed using the Law of Sines. The Law of Cosines, however, offers us a rare opportunity to find the remaining angles using only the data given to us in the statement of the problem. Using this, we get \(\gamma=\arccos \left(\frac{5}{7}\right) \text { radians } \approx 44.42^{\circ}\) and \(\alpha=\arccos \left(\frac{29}{35}\right) \text { radians } \approx 34.05^{\circ}\).

   

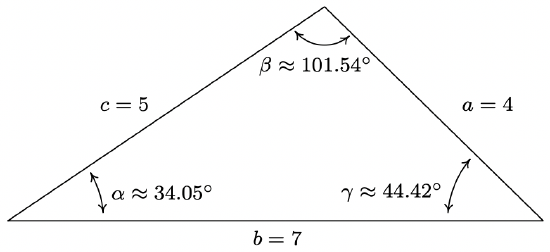
We note that, depending on how many decimal places are carried through successive calculations, and depending on which approach is used to solve the problem, the approximate answers you obtain may differ slightly from those the authors obtain in the Examples and the Exercises. A great example of this is number 2 in Example 11.3.1, where the approximate values we record for the measures of the angles sum to 180.01^◦ , which is geometrically impossible. Next, we have an application of the Law of Cosines

Example 11.3.2

A researcher wishes to determine the width of a vernal pond as drawn below. From a point \(P\), he finds the distance to the eastern-most point of the pond to be 950 feet, while the distance to the western-most point of the pond from \(P\) is 1000 feet. If the angle between the two lines of sight is 60^◦ , find the width of the pond.

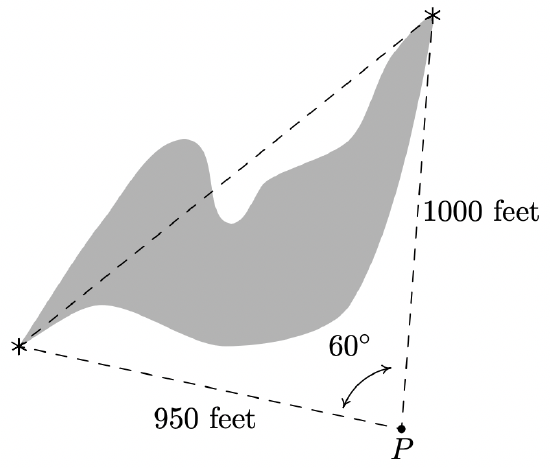
Solution

We are given the lengths of two sides and the measure of an included angle, so we may apply the Law of Cosines to find the length of the missing side opposite the given angle. Calling this length \(w\left(\text { for width), we get } w^{2}=950^{2}+1000^{2}-2(950)(1000) \cos \left(60^{\circ}\right)=952500\right.\) from which we get \(w=\sqrt{952500} \approx 976 \text { feet }\).

In Section 11.2, we used the proof of the Law of Sines to develop Theorem 11.4 as an alternate formula for the area enclosed by a triangle. In this section, we use the Law of Cosines to derive another such formula - Heron’s Formula.

Theorem 11.6. Heron’s Formula

Suppose \(a\), \(b\) and \(c\) denote the lengths of the three sides of a triangle. Let \(s\) be the semiperimeter of the triangle, that is, let \(s=\frac{1}{2}(a+b+c)\). Then the area \(A\) enclosed by the triangle is given by

\(A=\sqrt{s(s-a)(s-b)(s-c)}\)

We prove Theorem 11.6 using Theorem 11.4. Using the convention that the angle \(\gamma\) is opposite the side \(c\), we have \(A=\frac{1}{2} a b \sin (\gamma)\) from Theorem 11.4. In order to simplify computations, we start by manipulating the expression for \(A^{2}\).

\(\begin{aligned}
A^{2} &=\left(\frac{1}{2} a b \sin (\gamma)\right)^{2} \\
&=\frac{1}{4} a^{2} b^{2} \sin ^{2}(\gamma) \\
&=\frac{a^{2} b^{2}}{4}\left(1-\cos ^{2}(\gamma)\right) \quad \text { since } \sin ^{2}(\gamma)=1-\cos ^{2}(\gamma).
\end{aligned}\)

The Law of Cosines tells us \(\cos (\gamma)=\frac{a^{2}+b^{2}-c^{2}}{2 a b}\), so substituting this into our equation for \(A^{2}\) gives

\(\begin{aligned}
A^{2} &=\frac{a^{2} b^{2}}{4}\left(1-\cos ^{2}(\gamma)\right) \\
&=\frac{a^{2} b^{2}}{4}\left[1-\left(\frac{a^{2}+b^{2}-c^{2}}{2 a b}\right)^{2}\right] \\
&=\frac{a^{2} b^{2}}{4}\left[1-\frac{\left(a^{2}+b^{2}-c^{2}\right)^{2}}{4 a^{2} b^{2}}\right] \\
&=\frac{a^{2} b^{2}}{4}\left[\frac{4 a^{2} b^{2}-\left(a^{2}+b^{2}-c^{2}\right)^{2}}{4 a^{2} b^{2}}\right] \\
&\left.=\frac{4 a^{2} b^{2}-\left(a^{2}+b^{2}-c^{2}\right)^{2}}{16}\right] \\
&=\frac{(2 a b)^{2}-\left(a^{2}+b^{2}-c^{2}\right)^{2}}{16} \quad\quad\quad\quad \text { difference of squares. } \\
&=\frac{\left(2 a b-\left[a^{2}+b^{2}-c^{2}\right]\right)\left(2 a b+\left[a^{2}+b^{2}-c^{2}\right]\right)}{16} \\
&=\frac{\left(c^{2}-a^{2}+2 a b-b^{2}\right)\left(a^{2}+2 a b+b^{2}-c^{2}\right)}{16} \quad \text { os }
\end{aligned}\)

\(\begin{aligned} A^{2} &=\frac{\left(c^{2}-\left[a^{2}-2 a b+b^{2}\right]\right)\left(\left[a^{2}+2 a b+b^{2}\right]-c^{2}\right)}{16} \\ &=\frac{\left(c^{2}-(a-b)^{2}\right)\left((a+b)^{2}-c^{2}\right)}{16}\quad \text { perfect square trinomials. } \\ &=\frac{(c-(a-b))(c+(a-b))((a+b)-c)((a+b)+c)}{16} \quad \text { difference of squares. } \\ &=\frac{(b+c-a)(a+c-b)(a+b-c)(a+b+c)}{16} \\ &=\frac{(b+c-a)}{2} \cdot \frac{(a+c-b)}{2} \cdot \frac{(a+b-c)}{2} \cdot \frac{(a+b+c)}{2} \end{aligned}\)

At this stage, we recognize the last factor as the semiperimer, \(s=\frac{1}{2}(a+b+c)=\frac{a+b+c}{2}\). To complete the proof, we note that

\((s-a)=\frac{a+b+c}{2}-a=\frac{a+b+c-2 a}{2}=\frac{b+c-a}{2}\)

Similarly, we find \((s-b)=\frac{a+c-b}{2}\) and \((s-c)=\frac{a+b-c}{2}\). Hence, we get

\(\begin{aligned}
A^{2} &=\frac{(b+c-a)}{2} \cdot \frac{(a+c-b)}{2} \cdot \frac{(a+b-c)}{2} \cdot \frac{(a+b+c)}{2} \\
&=(s-a)(s-b)(s-c) s
\end{aligned}\)

so that \(A=\sqrt{s(s-a)(s-b)(s-c)}\) c) as required.

We close with an example of Heron’s Formula.

Example 11.3.3

Find the area enclosed of the triangle in Example 11.3.1 number 2.

Solution

We are given \(a = 4\), \(b = 7\) and \(c = 5\). Using these values, we find \(s=\frac{1}{2}(4+7+5)=8\), \((s-a)=8-4=4,(s-b)=8-7=1\) and \((s-c)=8-5=3\). Using Heron’s Formula, we get \(A=\sqrt{s(s-a)(s-b)(s-c)}=\sqrt{(8)(4)(1)(3)}=\sqrt{96}=4 \sqrt{6} \approx 9.80\) square units.

11.3.1 Exercises

In Exercises 1 - 10, use the Law of Cosines to find the remaining side(s) and angle(s) if possible.

1. \(a=7, b=12, \gamma=59.3^{\circ}\)
2. \(\alpha=104^{\circ}, b=25, c=37\)
3. \(\alpha=120^{\circ}, b=3, c=4\)
4. \(a=3, b=4, \gamma=90^{\circ}\)
5. \(\alpha=120^{\circ}, b=3, c=4\)
6. \(a=7, b=10, c=13\)
7. \(a=1, b=2, c=5\)
8. \(a=300, b=302, c=48\)
9. \(a=5, b=5, c=5\)
10. \(a=5, b=12, ; c=13\)

In Exercises 11 - 16, solve for the remaining side(s) and angle(s), if possible, using any appropriate technique.

11. \(a=18, \alpha=63^{\circ}, b=20\)
12. \(a=37, b=45, c=26\)
13. \(a=16, \alpha=63^{\circ}, b=20\)
14. \(a=22, \alpha=63^{\circ}, b=20\)
15. \(\alpha=42^{\circ}, b=117, c=88\)
16. \(\beta=7^{\circ}, \gamma=170^{\circ}, c=98.6\)
17. Find the area of the triangles given in Exercises 6, 8 and 10 above.
18. The hour hand on my antique Seth Thomas schoolhouse clock in 4 inches long and the minute hand is 5.5 inches long. Find the distance between the ends of the hands when the clock reads four o’clock. Round your answer to the nearest hundredth of an inch.
19. A geologist wants to measure the diameter of a crater. From her camp, it is 4 miles to the northern-most point of the crater and 2 miles to the southern-most point. If the angle between the two lines of sight is 117^◦ , what is the diameter of the crater? Round your answer to the nearest hundredth of a mile.
20. From the Pedimaxus International Airport a tour helicopter can fly to Cliffs of Insanity Point by following a bearing of N8.2^◦E for 192 miles and it can fly to Bigfoot Falls by following a bearing of S68.5^◦E for 207 miles.⁶ Find the distance between Cliffs of Insanity Point and Bigfoot Falls. Round your answer to the nearest mile.
21. Cliffs of Insanity Point and Bigfoot Falls from Exericse 20 above both lie on a straight stretch of the Great Sasquatch Canyon. What bearing would the tour helicopter need to follow to go directly from Bigfoot Falls to Cliffs of Insanity Point? Round your angle to the nearest tenth of a degree.
22. A naturalist sets off on a hike from a lodge on a bearing of S80^◦W. After 1.5 miles, she changes her bearing to S17^◦W and continues hiking for 3 miles. Find her distance from the lodge at this point. Round your answer to the nearest hundredth of a mile. What bearing should she follow to return to the lodge? Round your angle to the nearest degree.
23. The HMS Sasquatch leaves port on a bearing of N23^◦E and travels for 5 miles. It then changes course and follows a heading of S41^◦E for 2 miles. How far is it from port? Round your answer to the nearest hundredth of a mile. What is its bearing to port? Round your angle to the nearest degree.
24. The SS Bigfoot leaves a harbor bound for Nessie Island which is 300 miles away at a bearing of N32^◦E. A storm moves in and after 100 miles, the captain of the Bigfoot finds he has drifted off course. If his bearing to the harbor is now S70^◦W, how far is the SS Bigfoot from Nessie Island? Round your answer to the nearest hundredth of a mile. What course should the captain set to head to the island? Round your angle to the nearest tenth of a degree.
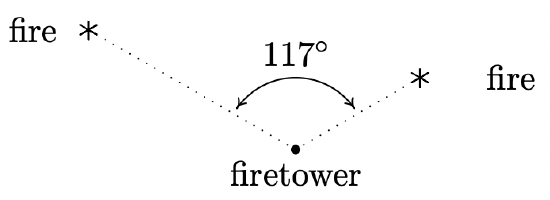
25. From a point 300 feet above level ground in a firetower, a ranger spots two fires in the Yeti National Forest. The angle of depression⁷ made by the line of sight from the ranger to the first fire is 2.5^◦ and the angle of depression made by line of sight from the ranger to the second fire is 1.3^◦ . The angle formed by the two lines of sight is 117^◦. Find the distance between the two fires. Round your answer to the nearest foot. (Hint: In order to use the 117^◦ angle between the lines of sight, you will first need to use right angle Trigonometry to find the lengths of the lines of sight. This will give you a Side-Angle-Side case in which to apply the Law of Cosines.)

    

26. If you apply the Law of Cosines to the ambiguous Angle-Side-Side (ASS) case, the result is a quadratic equation whose variable is that of the missing side. If the equation has no positive real zeros then the information given does not yield a triangle. If the equation has only one positive real zero then exactly one triangle is formed and if the equation has two distinct positive real zeros then two distinct triangles are formed. Apply the Law of Cosines to Exercises 11, 13 and 14 above in order to demonstrate this result.
27. Discuss with your classmates why Heron’s Formula yields an area in square units even though four lengths are being multiplied together.

11.3.2 Answers

1. \(\begin{array}{lll}
   \alpha \approx 35.54^{\circ} & \beta \approx 85.16^{\circ} & \gamma=59.3^{\circ} \\
   a=7 & b=12 & c \approx 10.36
   \end{array}\)
2. \(\begin{array}{lll}
   \alpha=104^{\circ} & \beta \approx 29.40^{\circ} & \gamma \approx 46.60^{\circ} \\
   a \approx 49.41 & b=25 & c=37
   \end{array}\)
3. \(\begin{array}{lll}
   \alpha \approx 85.90^{\circ} & \beta=8.2^{\circ} & \gamma \approx 85.90^{\circ} \\
   a=153 & b \approx 21.88 & c=153
   \end{array}\)
4. \(\begin{array}{lll}
   \alpha \approx 36.87^{\circ} & \beta \approx 53.13^{\circ} & \gamma=90^{\circ} \\
   a=3 & b=4 & c=5
   \end{array}\)
5. \(\begin{array}{lll}
   \alpha=120^{\circ} & \beta \approx 25.28^{\circ} & \gamma \approx 34.72^{\circ} \\
   a=\sqrt{37} & b=3 & c=4
   \end{array}\)
6. \(\begin{array}{lll}
   \alpha \approx 32.31^{\circ} & \beta \approx 49.58^{\circ} & \gamma \approx 98.21^{\circ} \\
   a=7 & b=10 & c=13
   \end{array}\)
7. Information does not produce a triangle
8. \(\begin{array}{lll}
   \alpha \approx 83.05^{\circ} & \beta \approx 87.81^{\circ} & \gamma \approx 9.14^{\circ} \\
   a=300 & b=302 & c=48
   \end{array}\)
9. \(\begin{array}{lll}
   \alpha=60^{\circ} & \beta=60^{\circ} & \gamma=60^{\circ} \\
   a=5 & b=5 & c=5
   \end{array}\)
10. \(\begin{array}{lll}
    \alpha \approx 22.62^{\circ} & \beta \approx 67.38^{\circ} & \gamma=90^{\circ} \\
    a=5 & b=12 & c=13
    \end{array}\)
11. \(\begin{array}{lll}
    \alpha=63^{\circ} & \beta \approx 98.11^{\circ} & \gamma \approx 18.89^{\circ} \\
    a=18 & b=20 & c \approx 6.54 \\
    \alpha=63^{\circ} & \beta \approx 81.89^{\circ} & \gamma \approx 35.11^{\circ} \\
    a=18 & b=20 & c \approx 11.62
    \end{array}\)
12. \(\begin{array}{lll}
    \alpha \approx 55.30^{\circ} & \beta \approx 89.40^{\circ} & \gamma \approx 35.30^{\circ} \\
    a=37 & b=45 & c=26
    \end{array}\)
13. Information does not produce a triangle
14. \(\begin{array}{lll}
    \alpha=63^{\circ} & \beta \approx 54.1^{\circ} & \gamma \approx 62.9^{\circ} \\
    a=22 & b=20 & c \approx 21.98
    \end{array}\)
15. \(\begin{array}{lll}
    \alpha=42^{\circ} & \beta \approx 89.23^{\circ} & \gamma \approx 48.77^{\circ} \\
    a \approx 78.30 & b=117 & c=88
    \end{array}\)
16. \(\begin{array}{lll}
    \alpha \approx 3^{\circ} & \beta=7^{\circ} & \gamma=170^{\circ} \\
    a \approx 29.72 & b \approx 69.2 & c=98.6
    \end{array}\)
17. The area of the triangle given in Exercise 6 is \(\sqrt{1200}=20 \sqrt{3} \approx 34.64\) square units.

    The area of the triangle given in Exercise 8 is \(\sqrt{51764375} \approx 7194.75\) square units.

    The area of the triangle given in Exercise 10 is exactly 30 square units.

18. The distance between the ends of the hands at four o’clock is about 8.26 inches.
19. The diameter of the crater is about 5.22 miles.
20. About 313 miles
21. N31.8^◦W
22. She is about 3.92 miles from the lodge and her bearing to the lodge is N37^◦E.
23. It is about 4.50 miles from port and its heading to port is S47^◦W.
24. It is about 229.61 miles from the island and the captain should set a course of N16.4^◦E to reach the island.
25. The fires are about 17456 feet apart. (Try to avoid rounding errors.)

---

Reference

¹ Here, ‘Side-Angle-Side’ means that we are given two sides and the ‘included’ angle - that is, the given angle is adjacent to both of the given sides.

² This shouldn’t come as too much of a shock. All of the theorems in Trigonometry can ultimately be traced back to the definition of the circular functions along with the distance formula and hence, the Pythagorean Theorem.

³ after simplifying . . .

⁴ Your instructor will let you know which procedure to use. It all boils down to how much you trust your calculator.

⁵ There can only be one obtuse angle in the triangle, and if there is one, it must be the largest.

⁶ Please refer to Page 905 in Section 11.2 for an introduction to bearings.

⁷ See Exercise 78 in Section 10.3 for the definition of this angle.