4.6: Exponential and Logarithmic Models
- Page ID
- 13855
While we have explored some basic applications of exponential and logarithmic functions, in this section we explore some important applications in more depth.
Radioactive Decay
In an earlier section, we discussed radioactive decay – the idea that radioactive isotopes change over time. One of the common terms associated with radioactive decay is half-life.
Definition: Half Life
The half-life of a radioactive isotope is the time it takes for half the substance to decay.
Given the basic exponential growth/decay equation \(h(t)=ab^{t}\), half-life can be found by solving for when half the original amount remains; by solving \(\dfrac{1}{2} a=a(b)^{t}\), or more simply \(\dfrac{1}{2} =b^{t}\). Notice how the initial amount is irrelevant when solving for half-life.
Example \(\PageIndex{1}\)
Bismuth-210 is an isotope that decays by about 13% each day. What is the half-life of Bismuth-210?
Solution
We were not given a starting quantity, so we could either make up a value or use an unknown constant to represent the starting amount. To show that starting quantity does not affect the result, let us denote the initial quantity by the constant a. Then the decay of Bismuth-210 can be described by the equation \(Q(d)=a(0.87)^{d}\).
To find the half-life, we want to determine when the remaining quantity is half the original: \(\dfrac{1}{2} a\). Solving,
\[\dfrac{1}{2} a=a(0.87)^{d}\nonumber\] Divide by \(a\),
\[\dfrac{1}{2} =0.87^{d}\nonumber\] Take the log of both sides
\[\log \left(\dfrac{1}{2} \right)=\log \left(0.87^{d} \right)\nonumber\] Use the exponent property of logs
\[\log \left(\dfrac{1}{2} \right)=d\log \left(0.87\right)\nonumber\] Divide to solve for \(d\)
\[d=\dfrac{\log \left(\dfrac{1}{2} \right)}{\log \left(0.87\right)} \approx 4.977\text{ days}\nonumber \]
This tells us that the half-life of Bismuth-210 is approximately 5 days.
Example \(\PageIndex{2}\)
Cesium-137 has a half-life of about 30 years. If you begin with 200 mg of cesium-137, how much will remain after 30 years? 60 years? 90 years?
Solution
Since the half-life is 30 years, after 30 years, half the original amount, 100 mg, will remain.
After 60 years, another 30 years have passed, so during that second 30 years, another half of the substance will decay, leaving 50 mg.
After 90 years, another 30 years have passed, so another half of the substance will decay, leaving 25 mg.
Example \(\PageIndex{3}\)
Cesium-137 has a half-life of about 30 years. Find the annual decay rate.
Solution
Since we are looking for an annual decay rate, we will use an equation of the form \(Q(t)=a(1+r)^{t}\). We know that after 30 years, half the original amount will remain. Using this information
\[\dfrac{1}{2} a=a(1+r)^{30}\nonumber\] Dividing by \(a\)
\[\dfrac{1}{2} =(1+r)^{30}\nonumber\] Taking the 30\({}^{th}\) root of both sides
\[\sqrt[{30}]{\dfrac{1}{2} } =1+r\nonumber\] Subtracting one from both sides,
\[r=\sqrt[{30}]{\dfrac{1}{2} } -1\approx -0.02284\nonumber\]
This tells us cesium-137 is decaying at an annual rate of 2.284% per year.
Exercise \(\PageIndex{1}\)
Chlorine-36 is eliminated from the body with a biological half-life of 10 days (www.ead.anl.gov/pub/doc/chlorine.pdf). Find the daily decay rate.
- Answer
-
\(r = \sqrt[10]{\dfrac{1}{2}} - 1 \approx -0.067\) or 6.7% is the daily rate of decay.
Example \(\PageIndex{4}\)
Carbon-14 is a radioactive isotope that is present in organic materials, and is commonly used for dating historical artifacts. Carbon-14 has a half-life of 5730 years. If a bone fragment is found that contains 20% of its original carbon-14, how old is the bone?
Solution
To find how old the bone is, we first will need to find an equation for the decay of the carbon-14. We could either use a continuous or annual decay formula, but opt to use the continuous decay formula since it is more common in scientific texts. The half life tells us that after 5730 years, half the original substance remains. Solving for the rate,
\[\dfrac{1}{2} a=ae^{r5730}\nonumber\] Dividing by \(a\)
\[\dfrac{1}{2} =e^{r5730}\nonumber\] Taking the natural log of both sides
\[\ln \left(\dfrac{1}{2} \right)=\ln \left(e^{r5730} \right)\nonumber\] Use the inverse property of logs on the right side
\[\ln \left(\dfrac{1}{2} \right)=5730r\nonumber\] Divide by 5730
\[r=\dfrac{\ln \left(\dfrac{1}{2} \right)}{5730} \approx -0.000121\nonumber\]
Now we know the decay will follow the equation \(Q(t)=ae^{-0.000121t}\). To find how old the bone fragment is that contains 20% of the original amount, we solve for \(t\) so that \(Q(t) = 0.20a\).
\[0.20a=ae^{-0.000121t}\nonumber\]
\[0.20=e^{-0.000121t}\nonumber\]
\[\ln (0.20)=\ln \left(e^{-0.000121t} \right)\nonumber\]
\[\ln (0.20)=-0.000121t\nonumber\]
\[t=\dfrac{\ln (0.20)}{-0.000121} \approx 13301\text{ years}\nonumber\]
The bone fragment is about 13,300 years old.
Exercise \(\PageIndex{2}\)
In Example 2, we learned that Cesium-137 has a half-life of about 30 years. If you begin with 200 mg of cesium-137, will it take more or less than 230 years until only 1 milligram remains?
- Answer
-
Less than 230 years, 229.3157 to be exact.
Doubling Time
For decaying quantities, we asked how long it takes for half the substance to decay. For growing quantities we might ask how long it takes for the quantity to double.
Definition: Doubling Time
The doubling time of a growing quantity is the time it takes for the quantity to double.
Given the basic exponential growth equation \(h(t)=ab^{t}\), doubling time can be found by solving for when the original quantity has doubled; by solving \(2a=a(b)^{x}\), or more simply \(2=b^{x}\). Like with decay, the initial amount is irrelevant when solving for doubling time.
Example \(\PageIndex{5}\)
Cancer cells sometimes increase exponentially. If a cancerous growth contained 300 cells last month and 360 cells this month, how long will it take for the number of cancer cells to double?
Solution
Defining \(t\) to be time in months, with \(t = 0\) corresponding to this month, we are given two pieces of data: this month, (0, 360), and last month, (-1, 300).
From this data, we can find an equation for the growth. Using the form \(C(t)=ab^{t}\), we know immediately a = 360, giving \(C(t)=360b^{t}\). Substituting in (-1, 300), \[\begin{array}{l} {300=360b^{-1} } \\ {300=\dfrac{360}{b} } \\ {b=\dfrac{360}{300} =1.2} \end{array}\nonumber\]
This gives us the equation \(C(t)=360(1.2)^{t}\)
To find the doubling time, we look for the time when we will have twice the original amount, so when \(C(t) = 2a\).
\[2a=a(1.2)^{t}\nonumber\]
\[2=(1.2)^{t}\nonumber\]
\[\log \left(2\right)=\log \left(1.2^{t} \right)\nonumber\]
\[\log \left(2\right)=t\log \left(1.2\right)\nonumber\]
\[t=\dfrac{\log \left(2\right)}{\log \left(1.2\right)} \approx 3.802\nonumber\] months for the number of cancer cells to double.
Example \(\PageIndex{6}\)
Use of a new social networking website has been growing exponentially, with the number of new members doubling every 5 months. If the site currently has 120,000 users and this trend continues, how many users will the site have in 1 year?
Solution
We can use the doubling time to find a function that models the number of site users, and then use that equation to answer the question. While we could use an arbitrary a as we have before for the initial amount, in this case, we know the initial amount was 120,000.
If we use a continuous growth equation, it would look like \(N(t)=120e^{rt}\), measured in thousands of users after t months. Based on the doubling time, there would be 240 thousand users after 5 months. This allows us to solve for the continuous growth rate:
\[240=120e^{r5}\nonumber\]
\[2=e^{r5}\nonumber\]
\[\ln 2=5r\nonumber\]
\[r=\dfrac{\ln 2}{5} \approx 0.1386\nonumber\]
Now that we have an equation, \(N(t)=120e^{0.1386t}\), we can predict the number of users after 12 months:
\[N(12) =120e^{0.1386(12)} =633.140\text{ thousand users}\nonumber\].
So after 1 year, we would expect the site to have around 633,140 users.
Exercise \(\PageIndex{3}\)
If tuition at a college is increasing by 6.6% each year, how many years will it take for tuition to double?
- Answer
-
Solving \(a (1 + 0.066)^t = 2a\), it will take \(t = \dfrac{log(2)}{log(1.066)} \approx 10.845\) years, or approximately 11 years, for tuition to double.
Newton’s Law of Cooling
When a hot object is left in surrounding air that is at a lower temperature, the object’s temperature will decrease exponentially, leveling off towards the surrounding air temperature. This "leveling off" will correspond to a horizontal asymptote in the graph of the temperature function. Unless the room temperature is zero, this will correspond to a vertical shift of the generic exponential decay function.
Definition: Newton’s Law of Cooling
The temperature of an object, \(T\), in surrounding air with temperature \(T_{s}\) will behave according to the formula
\[T(t)=ae^{kt} +T_{s}\]
Where
- \(t\) is time
- \(a\) is a constant determined by the initial temperature of the object
- \(k\) is a constant, the continuous rate of cooling of the object
While an equation of the form \(T(t)=ab^{t} +T_{s}\) could be used, the continuous growth form is more common.
Example \(\PageIndex{7}\)
A cheesecake is taken out of the oven with an ideal internal temperature of 165 degrees Fahrenheit, and is placed into a 35 degree refrigerator. After 10 minutes, the cheesecake has cooled to 150 degrees. If you must wait until the cheesecake has cooled to 70 degrees before you eat it, how long will you have to wait?
Solution
Since the surrounding air temperature in the refrigerator is 35 degrees, the cheesecake’s temperature will decay exponentially towards 35, following the equation
\[T(t)=ae^{kt} +35\nonumber\]
We know the initial temperature was 165, so \(T(0)=165\). Substituting in these values,
\[\begin{array}{l} {165=ae^{k0} +35} \\ {165=a+35} \\ {a=130} \end{array}\nonumber\]
We were given another pair of data, \(T(10)=150\), which we can use to solve for \(k\)
\[150=130e^{k10} +35\nonumber\]
\[\begin{array}{l} {115=130e^{k10} } \\ {\dfrac{115}{130} =e^{10k} } \\ {\ln \left(\dfrac{115}{130} \right)=10k} \\ {k=\dfrac{\ln \left(\dfrac{115}{130} \right)}{10} =-0.0123} \end{array}\nonumber\]
Together this gives us the equation for cooling: \[T(t)=130e^{-0.0123t} +35\nonumber\]
Now we can solve for the time it will take for the temperature to cool to 70 degrees.
\[70=130e^{-0.0123t} +35\nonumber\]
\[35=130e^{-0.0123t}\nonumber\]
\[\dfrac{35}{130} =e^{-0.0123t}\nonumber\]
\[\ln \left(\dfrac{35}{130} \right)=-0.0123t\nonumber\]
\[t=\dfrac{\ln \left(\dfrac{35}{130} \right)}{-0.0123} \approx 106.68\nonumber\]
It will take about 107 minutes, or one hour and 47 minutes, for the cheesecake to cool. Of course, if you like your cheesecake served chilled, you’d have to wait a bit longer.
Exercise \(\PageIndex{4}\)
A pitcher of water at 40 degrees Fahrenheit is placed into a 70 degree room. One hour later the temperature has risen to 45 degrees. How long will it take for the temperature to rise to 60 degrees?
- Answer
-
\(T(t) = ae^{kt} + 70\). Substituting (0, 40), we find \(a = -30\). Substituting (1, 45), we solve \[45 = -30 e^{k(1)} + 70\nonumber\] to get \[k = ln(\dfrac{25}{30}) = -0.1823\nonumber\]
Solving \(60 = -30e^{-0.1823t} + 70\) gives
\[t = \dfrac{ln(1/3)}{-0.1823} = 6.026\text{ hours}\nonumber \]
Logarithmic Scales
For quantities that vary greatly in magnitude, a standard scale of measurement is not always effective, and utilizing logarithms can make the values more manageable. For example, if the average distances from the sun to the major bodies in our solar system are listed, you see they vary greatly.
| Planet | Distance (millions of km) |
| Mercury | 58 |
| Venus | 108 |
| Earth | 150 |
| Mars | 228 |
| Jupiter | 779 |
| Saturn | 1430 |
| Uranus | 2880 |
| Neptune | 4500 |
Placed on a linear scale – one with equally spaced values – these values get bunched up.

0 500 1000 1500 2000 2500 3000 3500 4000 4500
However, computing the logarithm of each value and plotting these new values on a number line results in a more manageable graph, and makes the relative distances more apparent.(It is interesting to note the large gap between Mars and Jupiter on the log number line. The asteroid belt is located there, which scientists believe is a planet that never formed because of the effects of the gravity of Jupiter.)
| Planet | Distance (millions of km) | log(distance) |
| Mercury | 58 | 1.76 |
| Venus | 108 | 2.03 |
| Earth | 150 | 2.18 |
| Mars | 228 | 2.36 |
| Jupiter | 779 | 2.89 |
| Saturn | 1430 | 3.16 |
| Uranus | 2880 | 3.46 |
| Neptune | 4500 | 3.65 |
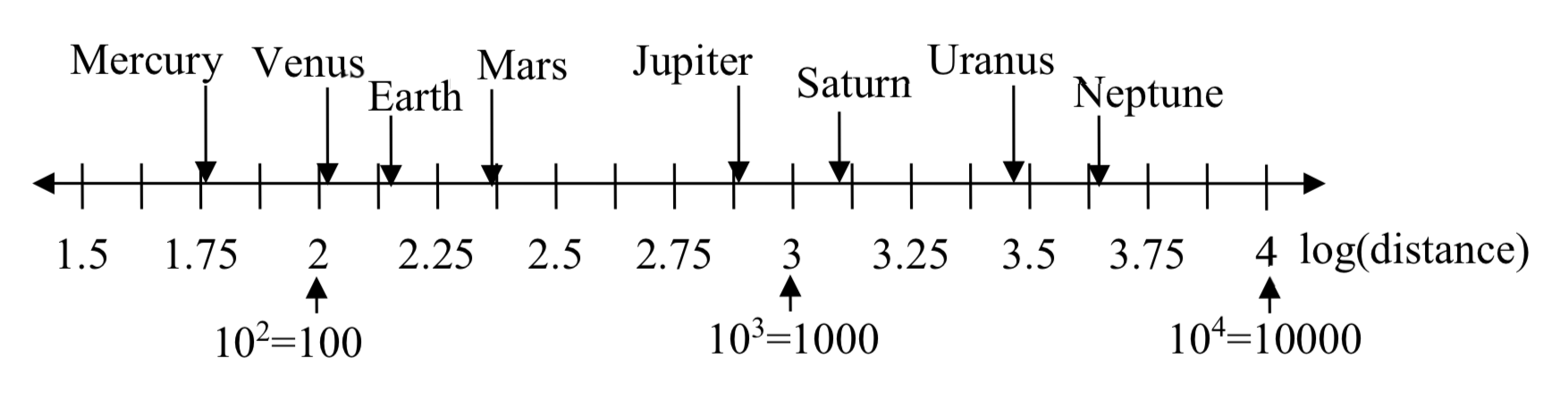
Sometimes, as shown above, the scale on a logarithmic number line will show the log values, but more commonly the original values are listed as powers of 10, as shown below.

Example \(\PageIndex{8}\)
Estimate the value of point \(P\) on the log scale above
The point \(P\) appears to be half way between -2 and -1 in log value, so if \(V\) is the value of this point,
\[\log (V)\approx -1.5\nonumber\] Rewriting in exponential form,
\[V\approx 10^{-1.5} =0.0316\nonumber\]
Example \(\PageIndex{9}\)
Place the number 6000 on a logarithmic scale.
Solution
Since \(\log (6000)\approx 3.8\), this point would belong on the log scale about here:

Exercise \(\PageIndex{5}\)
Plot the data in the table below on a logarithmic scale (From http://www.epd.gov.hk/epd/noise_educ...1/intro_5.html, retrieved Oct 2, 2010).
| Source of Sound/Noise | Approximate Sound Pressure in \(\mu\) Pa (micro Pascals) |
| Launching of the Space Shuttle | 2000,000,000 |
| Full Symphony Orchestra | 2000,000 |
| Diesel Freight Train at High Speed at 25 m | 200,000 |
| Normal Conversation | 20,000 |
| Soft Whispering at 2 m in Library | 2,000 |
| Unoccupied Broadcast Studio | 200 |
| Softest Sound a human can hear | 20 |
- Answer
-
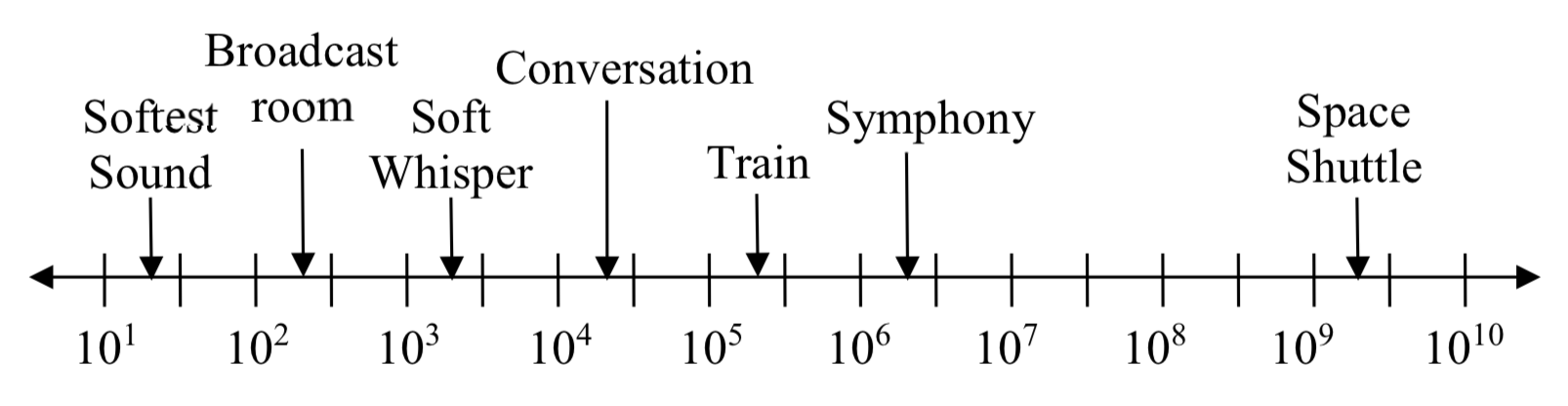
Notice that on the log scale above Example 8, the visual distance on the scale between points \(A\) and \(B\) and between \(C\) and \(D\) is the same. When looking at the values these points correspond to, notice \(B\) is ten times the value of \(A\), and \(D\) is ten times the value of \(C\). A visual \(linear\) difference between points corresponds to a relative (ratio) change between the corresponding values.
Logarithms are useful for showing these relative changes. For example, comparing $1,000,000 to $10,000, the first is 100 times larger than the second.
\[\dfrac{1,000,000}{10,000} = 100 = 10^2\nonumber\]
Likewise, comparing $1000 to $10, the first is 100 times larger than the second.
\[\dfrac{1,000}{10} = 100 = 10^2\nonumber\]
When one quantity is roughly ten times larger than another, we say it is one order of magnitude larger. In both cases described above, the first number was two orders of magnitude larger than the second.
Notice that the order of magnitude can be found as the common logarithm of the ratio of the quantities. On the log scale above, B is one order of magnitude larger than \(A\), and \(D\) is one order of magnitude larger than \(C\).
Definition: Orders of magnitude
Given two values \(A\) and \(B\), to determine how many orders of magnitude \(A\) is greater than \(B\),
Difference in orders of magnitude = log(\(\dfrac{A}{B})\)
Example \(\PageIndex{10}\)
On the log scale above Example 8, how many orders of magnitude larger is \(C\) than \(B\)?
Solution
The value \(B\) corresponds to \(10^2 = 100\)
The value \(C\) corresponds to \(10^5 = 100,000\)
The relative change is \(\dfrac{100,000}{100} = 1000 = \dfrac{10^5}{10^2} = 10^3\). The log of this value is 3.
\(C\) is three orders of magnitude greater than \(B\), which can be seen on the log scale by the visual difference between the points on the scale.
Exercise \(\PageIndex{6}\)
Using the table from Try it Now #5, what is the difference of order of magnitude between the softest sound a human can hear and the launching of the space shuttle?
- Answer
-
\(\dfrac{2 \times 10^9}{2 \times 10^1} = 10^8\). The sound pressure in \(\mu\)Pa created by launching the space shuttle is 8 orders of magnitude greater than the sound pressure in \(\mu\)Pa created by the softest sound a human ear can hear.
Earthquakes
An example of a logarithmic scale is the Moment Magnitude Scale (MMS) used for earthquakes. This scale is commonly and mistakenly called the Richter Scale, which was a very similar scale succeeded by the MMS.
Moment Magnitude Scale
For an earthquake with seismic moment \(S\), a measurement of earth movement, the MMS value, or magnitude of the earthquake, is
\[M = \dfrac{2}{3} log(\dfrac{S}{S_0})\]
Where \(S_0 = 10^{16}\) is a baseline measure for the seismic moment.
Example \(\PageIndex{11}\)
If one earthquake has a MMS magnitude of 6.0, and another has a magnitude of 8.0, how much more powerful (in terms of earth movement) is the second earthquake?
Solution
Since the first earthquake has magnitude 6.0, we can find the amount of earth movement for that quake, which we'll denote \(S_1\). The value of \(S_0\) is not particularity relevant, so we will not replace it with its value.
\[6.0 = \dfrac{2}{3} log (\dfrac{S_1}{S_0})\nonumber\]
\[6.0 (\dfrac{3}{2} = log (\dfrac{S_1}{S_0})\nonumber\]
\[9 = log(\dfrac{S_1}{S_0})\nonumber\]
\[\dfrac{S_1}{S_0} = 10^9\nonumber\]
\[S_1 = 10^9 S_0\nonumber\]
This tells us the first earthquake has about \(10^9\) times more earth movement than the baseline measure.
Doing the same with the second earthquake, \(S_2\), with a magnitude of 8.0,
\[8.0 = \dfrac{2}{3} log (\dfrac{S_2}{S_0})\nonumber\]
\[S_2 = 10^{12} S_0\nonumber\]
Comparing the earth movement of the second earthquake to the first,
\[\dfrac{S_2}{S_1} = \dfrac{10^{12} S_0} {10^9 S_0} = 10^3 = 1000\nonumber\]
The second value's earth movement is 1000 times as large as the first earthquake.
Example \(\PageIndex{12}\)
One earthquake has magnitude of 3.0. If a second earthquake has twice as much earth movement as the first earthquake, find the magnitude of the second quake.
Solution
Since the first quake has magnitude 3.0,
\[3.0 = \dfrac{2}{3} log (\dfrac{S}{S_0})\nonumber\]
Solving for \(S\),
\[3.0 \dfrac{3}{2} = log (\dfrac{S}{S_0})\nonumber\]
\[4.5 = log (\dfrac{S}{S_0})\nonumber\]
\[10^{4.5} = \dfrac{S}{S_0}\nonumber\]
\[S = 10^{4.5} S_0\nonumber\]
Since the second earthquake has twice as much earth movement, for the second quake,
\[S = 2 \cdot 10^{4.5} S_0\nonumber\]
Finding the magnitude,
\[M = \dfrac{2}{3} log (\dfrac{2 \cdot 10^{4.5} S_0}{S_0})\nonumber\]
\[M = \dfrac{2}{3} log (2 \cdot 10^{4.5}) \approx 3.201\nonumber\]
The second earthquake with twice as much earth movement will have a magnitude of about 3.2.
In fact, using log properties, we could show that whenever the earth movement doubles, the magnitude will increase by about 0.201:
\[M = \dfrac{2}{3} log (\dfrac{2S}{S_0}) = \dfrac{2}{3} log (2 \cdot \dfrac{S}{S_0})\nonumber\]
\[M = \dfrac{2}{3} (log(2) + log(\dfrac{S}{S_0}))\nonumber\]
\[M = \dfrac{2}{3} log (2) + \dfrac{2}{3} log (\dfrac{S}{S_0})\nonumber\]
\[M = 0.201 + \dfrac{2}{3} log (\dfrac{S}{S_0})\nonumber\]
This illustrates the most important feature of a log scale: that \(multiplying\) the quantity being considered will \(add\) to the scale value, and vice versa.
Important Topics of this Section
- Radioactive decay
- Half life
- Doubling time
- Newton’s law of cooling
- Logarithmic Scales
- Orders of Magnitude
- Moment Magnitude scale


