4.5E: Graphs of Logarithmic Functions (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
section 4.5 exercise
For each function, find the domain and the vertical asymptote.
1. f(x)=log(x−5)
2. f(x)=log(x+2)
3. f(x)=ln(3−x)
4. f(x)=ln(5−x)
5. f(x)=log(3x+1)
6. f(x)=log(2x+5)
7. f(x)=3log(−x)+2
8. f(x)=2log(−x)+1
Sketch a graph of each pair of functions.
9. f(x)=log(x),g(x)=ln(x)
10. f(x)=log2(x),g(x)=log4(x)
Sketch each transformation.
11. f(x)=2log(x)
12. f(x)=3ln(x)
13. f(x)=ln(−x)
14. f(x)=−log(x)
15. f(x)=log2(x+2)
16. f\left(x\right)=\log _{3} \left(x+4\right)\]
Find a formula for the transformed logarithm graph shown.
17. 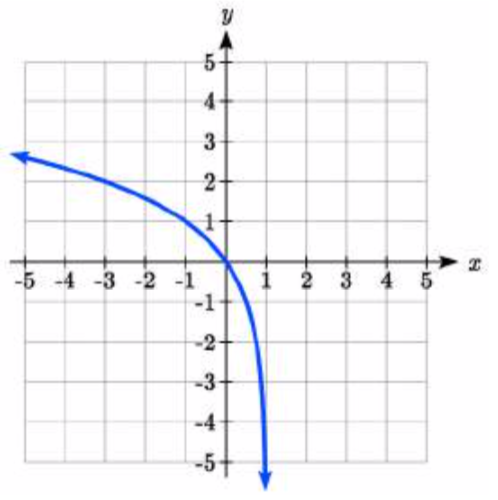 18.
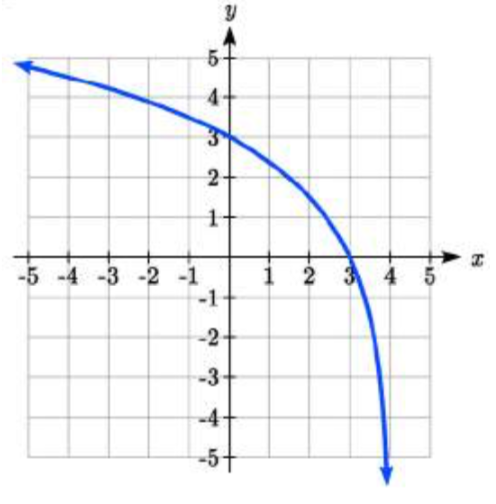
18. 
19. 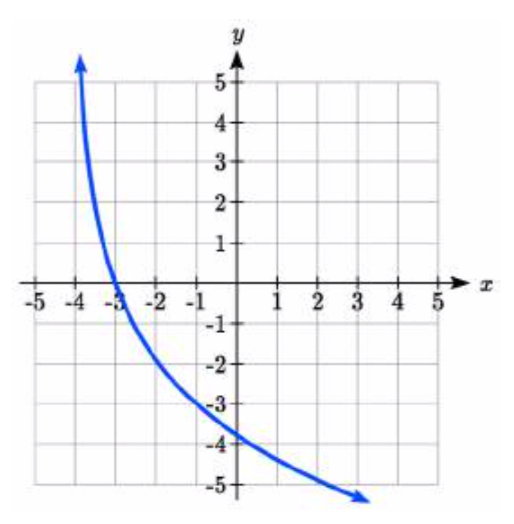 20.
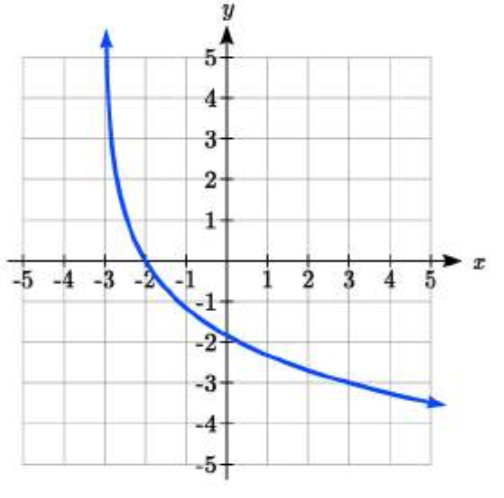
20. 
Find a formula for the transformed logarithm graph shown.
21. 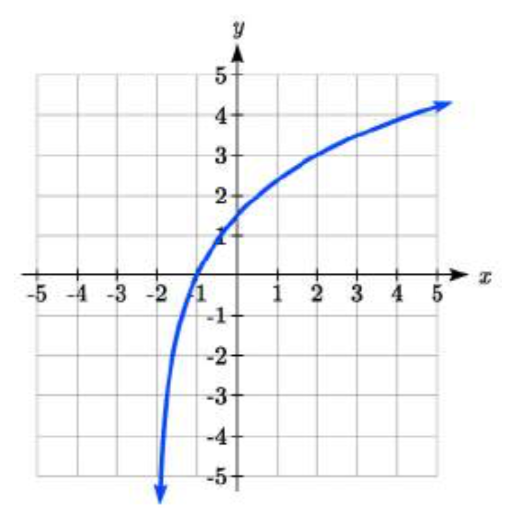 22.
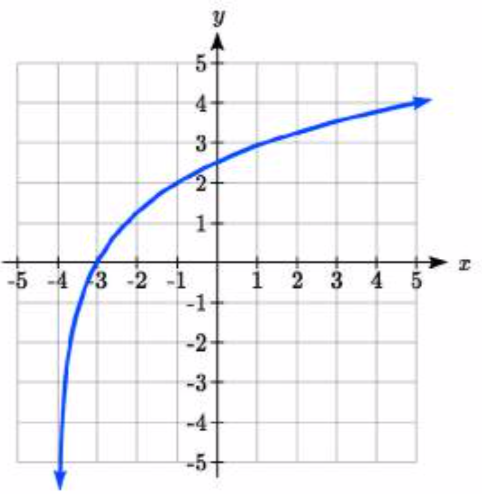
22.
23. 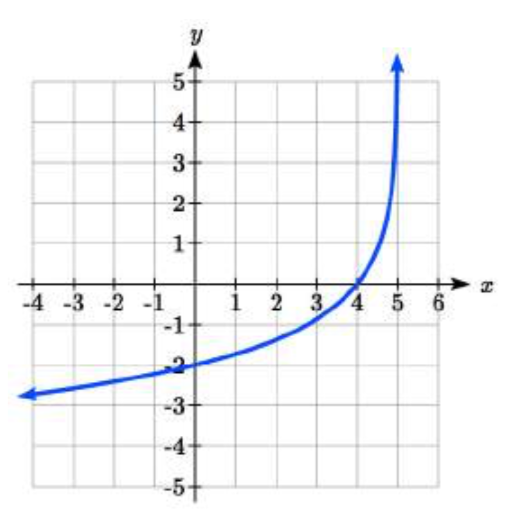 24.
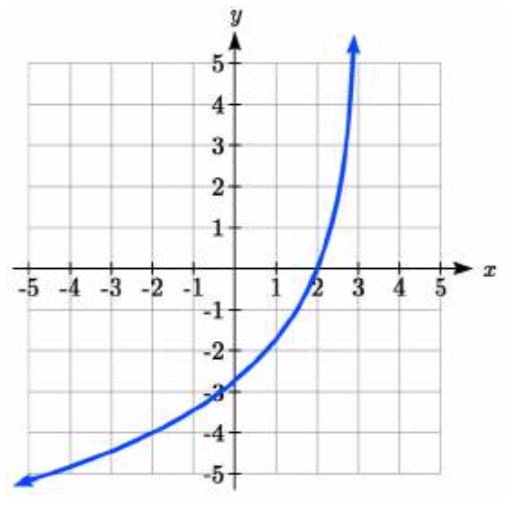
24.
- Answer
-
1. Domain: x>5 V. A. @ x=5
3. Domain: x<5 V. A. @ x=3
5. Domain: x>−13 V. A. @ x=−13
7. Domain: x<0 V. A. @ x=0
9.
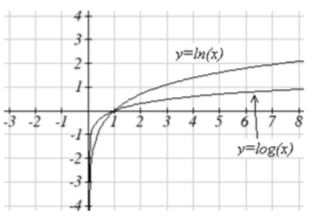
11.
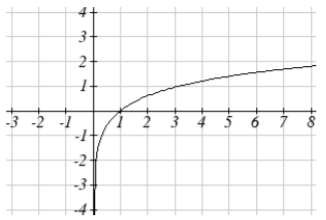
13.
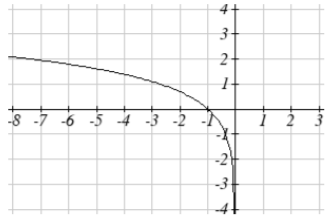
15.
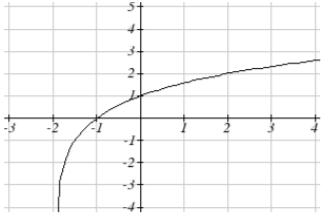
17. y=1log(2)log(−(x−1))
19. y=−3log(3)log(x+4)
21. y=3log(4)log(x+2)
23. y=−2log(5)log(−(x−5))


