6.1E: Sinusoidal Graphs (Exercises)
- Page ID
- 13923
Section 6.1 Exercises
1. Sketch a graph of \(f\left(x\right)=-3\sin \left(x\right)\).
2. Sketch a graph of \(f\left(x\right)=4\sin \left(x\right)\).
3. Sketch a graph of \(f\left(x\right)=2\cos \left(x\right)\).
4. Sketch a graph of \(f\left(x\right)=-4\cos \left(x\right)\).
For the graphs below, determine the amplitude, midline, and period, then find a formula for the function.
5. 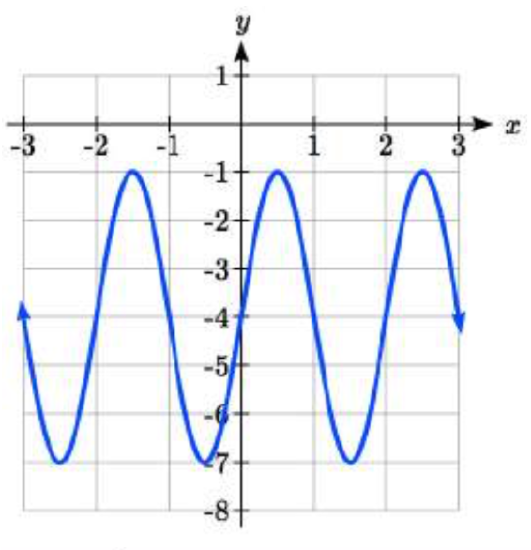 6.
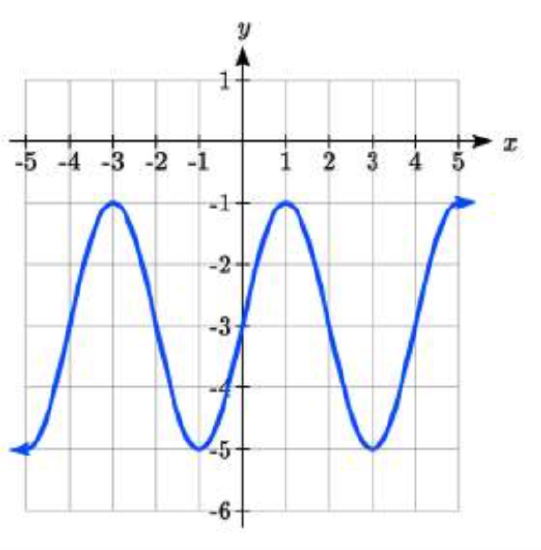
6. 
7. 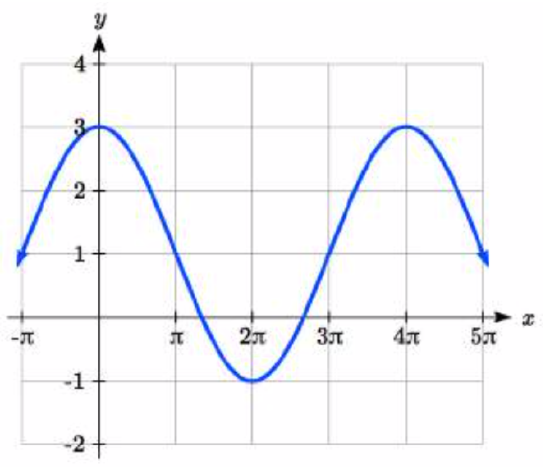 8.
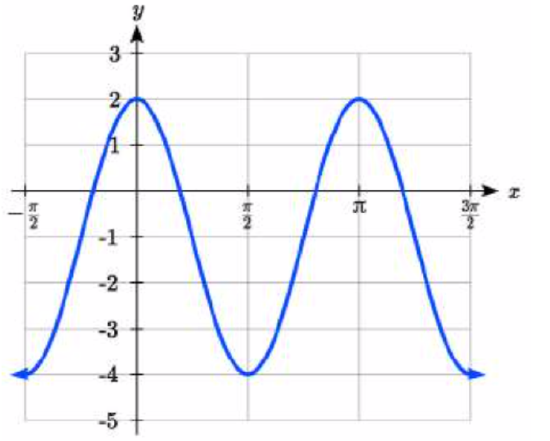
8. 
9. 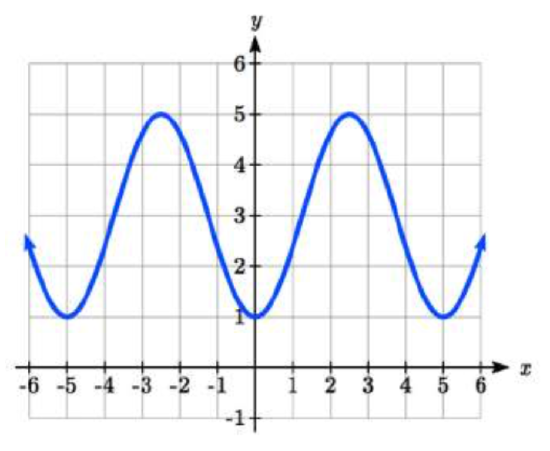 10.
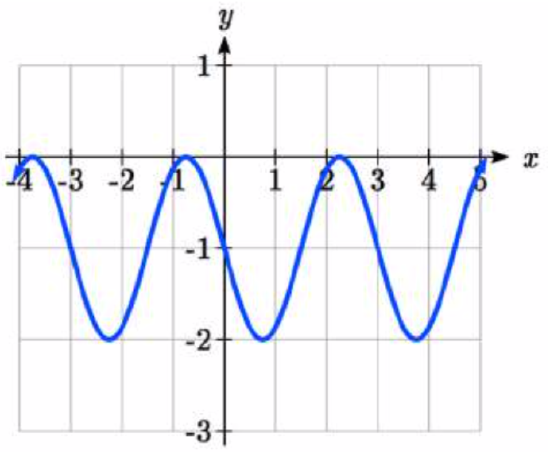
10.
For each of the following equations, find the amplitude, period, horizontal shift, and midline.
11. \(y=3\sin (8(x+4))+5\)
12. \(y=4\sin \left(\dfrac{\pi }{2} (x-3)\right)+7\)
13. \(y=2\sin (3x-21)+4\)
14. \(y=5\sin (5x+20)-2\)
15. \(y=\sin \left(\dfrac{\pi }{6} x+\pi \right)-3\)
16. \(y=8\sin \left(\dfrac{7\pi }{6} x+\dfrac{7\pi }{2} \right)+6\)
Find a formula for each of the functions graphed below.
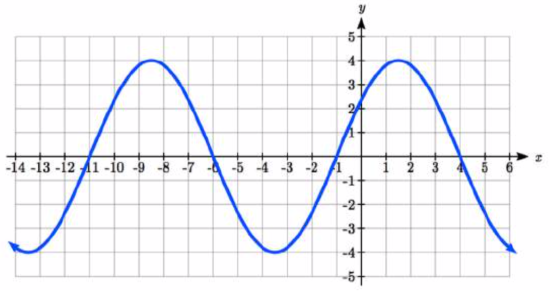
17. 
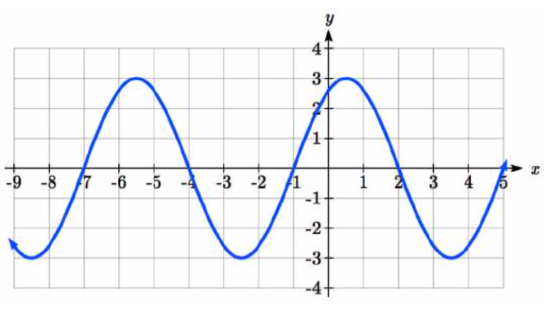
18. 
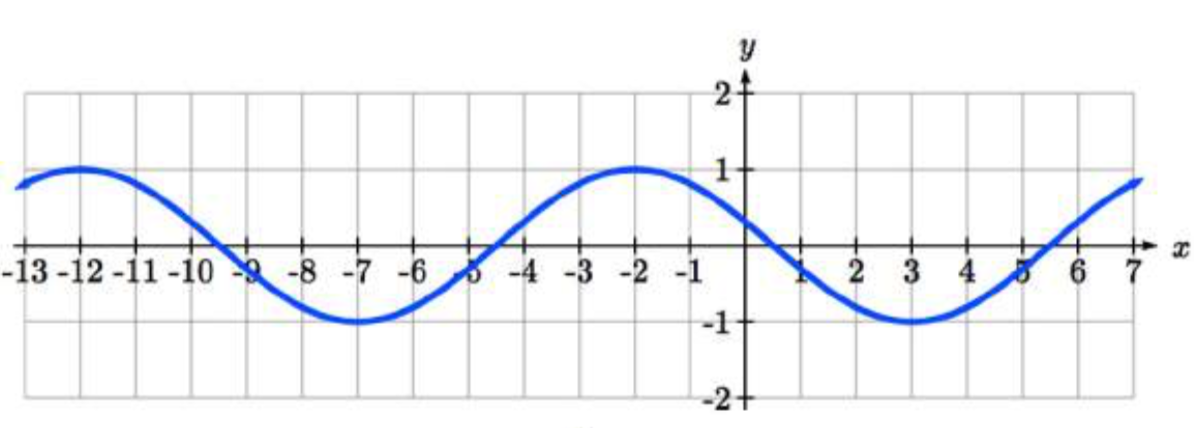
19. 
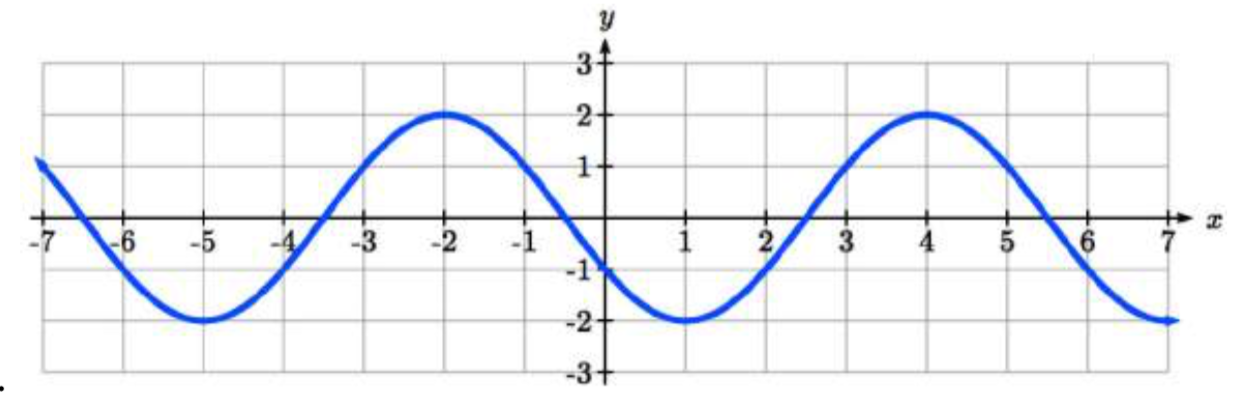
20. 
21. Outside temperature over the course of a day can be modeled as a sinusoidal function. Suppose you know the temperature is 50 degrees at midnight and the high and low temperature during the day are 57 and 43 degrees, respectively. Assuming t is the number of hours since midnight, find a function for the temperature, D, in terms of t.
22. Outside temperature over the course of a day can be modeled as a sinusoidal function. Suppose you know the temperature is 68 degrees at midnight and the high and low temperature during the day are 80 and 56 degrees, respectively. Assuming t is the number of hours since midnight, find a function for the temperature, D, in terms of t.
23. A Ferris wheel is 25 meters in diameter and boarded from a platform that is 1 meters above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 10 minutes. The function \(h(t)\) gives your height in meters above the ground t minutes after the wheel begins to turn.
a. Find the amplitude, midline, and period of \(h\left(t\right)\).
b. Find a formula for the height function \(h\left(t\right)\).
c. How high are you off the ground after 5 minutes?
24. A Ferris wheel is 35 meters in diameter and boarded from a platform that is 3 meters above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 8 minutes. The function \(h(t)\) gives your height in meters above the ground t minutes after the wheel begins to turn.
a. Find the amplitude, midline, and period of \(h\left(t\right)\).
b. Find a formula for the height function \(h\left(t\right)\).
c. How high are you off the ground after 4 minutes?
- Answer
-
1.
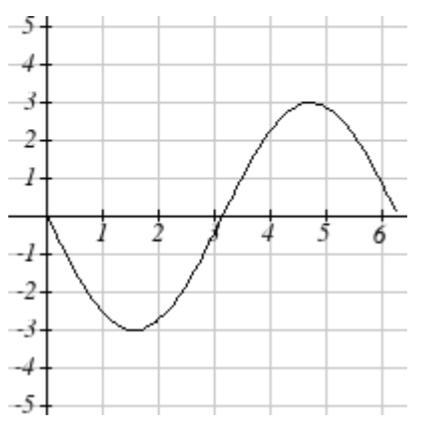
3.
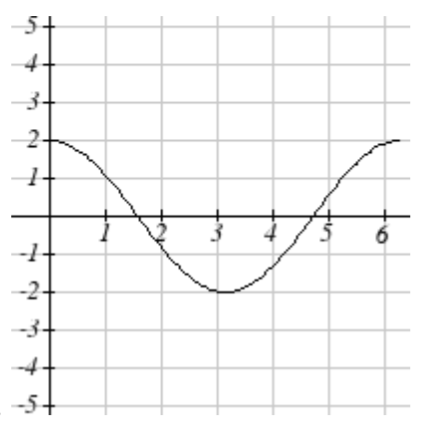
5. Amp: 3. Period = 2. Midline: \(y = -4\). \(f(t) = 3\sin(\pi t) - 4\)
7. Amp: 2. Period = \(4\pi\). Midline: \(y = 1\). \(f(t) = 2\cos(\dfrac{1}{2} t) + 1\)
9. Amp: 2. Period = 5. Midline: \(y = 3\). \(f(t) = -2\cos(\dfrac{2\pi}{5} t) + 3\)
11. Amp: 3, Period = \(\dfrac{\pi}{4}\), Shift: 4 left, Midline: \(y = 5\)
13. Amp: 2, Period = \(\dfrac{2\pi}{3}\), Shift: 7 left, Midline: \(y = 4\)
15. Amp: 1, Period = 12, Shift: 6 left, Midline: \(y = -3\)
17. \(f(x) = 4\sin(\dfrac{\pi}{5} (x + 1))\)
19. \(f(x) = \cos(\dfrac{\pi}{5} (x + 2))\)
21. \(D(t) = 50 - 7 \sin(\dfrac{\pi}{12}t)\)
23. a. Amp: 12.5. Midline: \(y = 13.5\). Period: 10
b. \(h(t) = -12.5 \cos(\dfrac{\pi}{5}t) + 13.5\)
c. \(h(t) = 26\) meters


