Skip to main content
\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)
Mathematics LibreTexts

6.2E: Graphs of the Other Trigonometric Functions (Exercises)

  1. Last updated
  2. Save as PDF
  • Page ID
    13924

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    Section 6.2 Exercises

    Match each trigonometric function with one of the graphs.

    1. \(f\left(x\right)=\tan \left(x\right)\)

    2. \(f\left(x\right)=\sec \left(x\right)\)

    3. \(f\left(x\right)=\csc (x)\)

    4. \(f\left(x\right)=\cot \left(x\right)\)

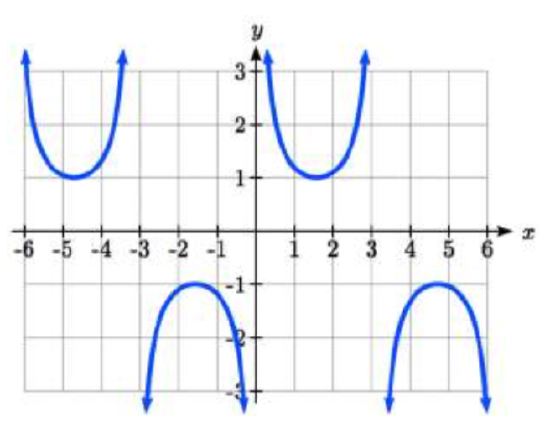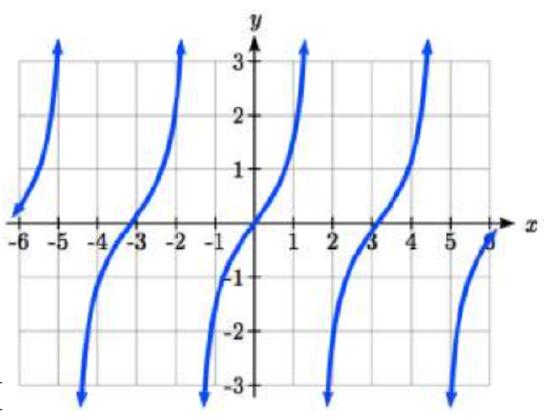
    I 屏幕快照 2019-07-09 上午4.10.09.png II屏幕快照 2019-07-09 上午4.10.28.png

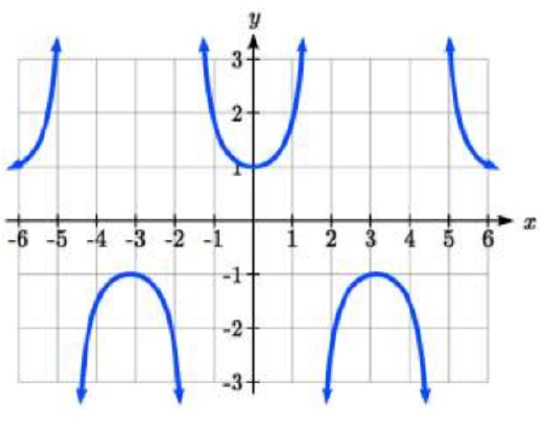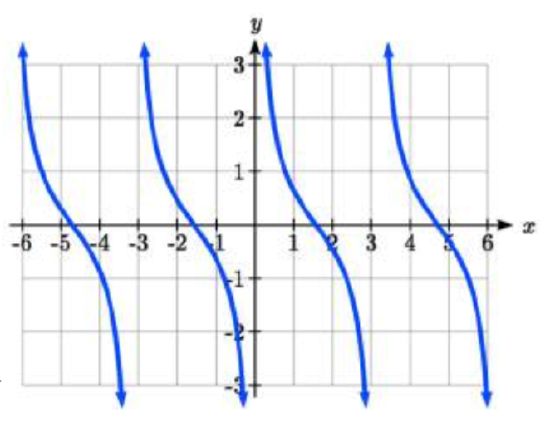
    III 屏幕快照 2019-07-09 上午4.10.47.png IV屏幕快照 2019-07-09 上午4.11.08.png

    Find the period and horizontal shift of each of the following functions.

    5. \(f\left(x\right)=2\tan \left(4x-32\right)\)

    6. \(g\left(x\right)=3\tan \left(6x+42\right)\)

    7. \(h\left(x\right)=2\sec \left(\frac{\pi }{4} \left(x+1\right)\right)\)

    8. \(k\left(x\right)=3\sec \left(2\left(x+\frac{\pi }{2} \right)\right)~\)

    9. \(m\left(x\right)=6\csc \left(\frac{\pi }{3} x+\pi \right)\)

    10. \(n\left(x\right)=4\csc \left(\frac{5\pi }{3} x-\frac{20\pi }{3} \right)\)

    11. Sketch a graph of #7 above.

    12. Sketch a graph of #8 above.

    13. Sketch a graph of #9 above.

    14. Sketch a graph of #10 above.

    15. Sketch a graph of \(j\left(x\right)=\tan \left(\frac{\pi }{2} x\right)\).

    16. Sketch a graph of \(p\left(t\right)=2\tan \left(t-\frac{\pi }{2} \right)\).

    Find a formula for each function graphed below.

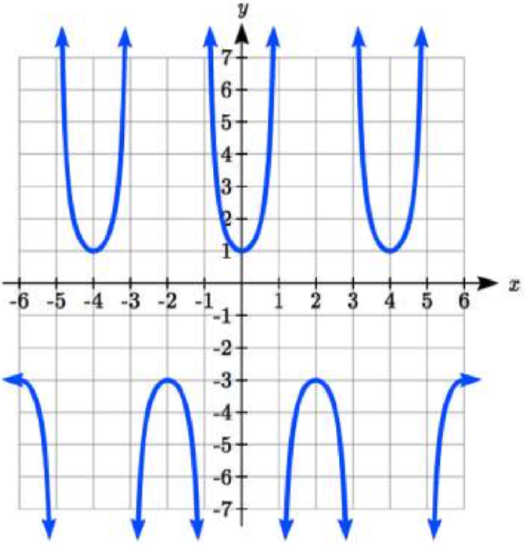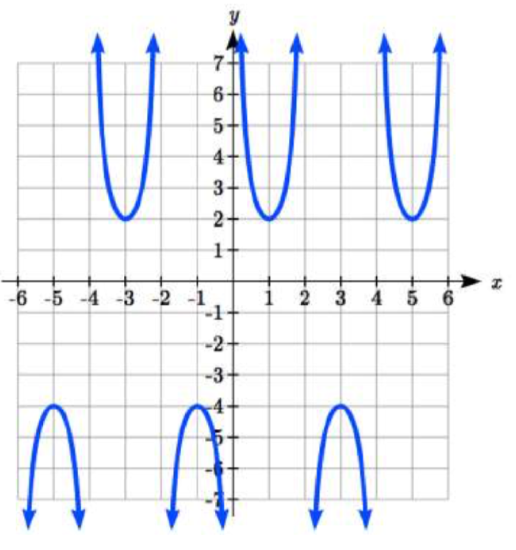
    17. 屏幕快照 2019-07-09 上午4.12.29.png18. 屏幕快照 2019-07-09 上午4.14.13.png

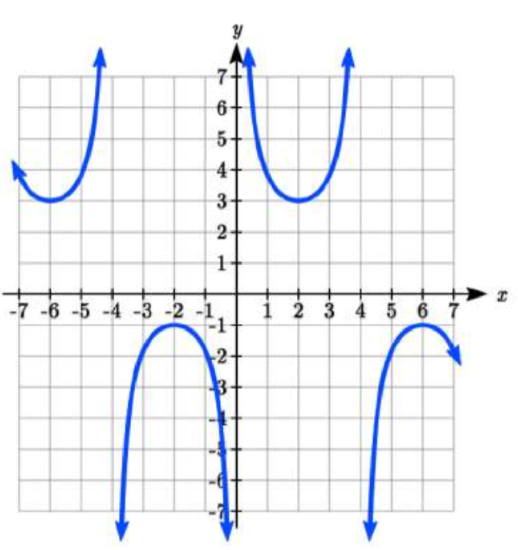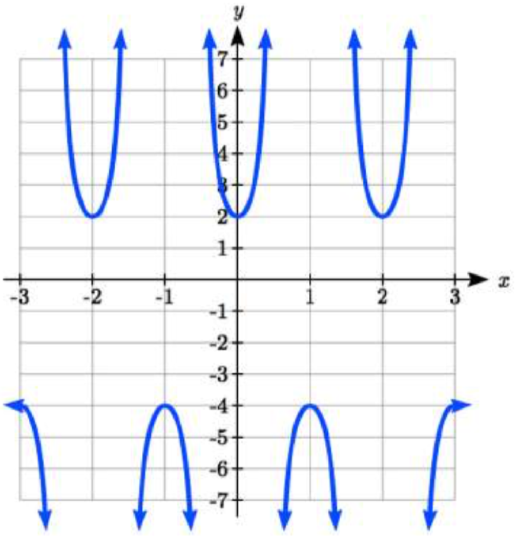
    19. 屏幕快照 2019-07-09 上午4.14.33.png20. 屏幕快照 2019-07-09 上午4.14.56.png

    21. If \(\tan x=-1.5\), find \(\tan \left(-x\right)\).

    22. If \(\tan x=3\), find \(\tan \left(-x\right)\).

    23. If \(\sec x=2\), find \(\sec \left(-x\right)\).

    24. If \(\sec x=-4\), find \(\sec \left(-x\right)\).

    25. If \(\csc x=-5\), find \(\csc \left(-x\right)\).

    26. If \(\csc x=2\), find \(\csc \left(-x\right)\).

    Simplify each of the following expressions completely.

    27. \(\cot \left(-x\right)\cos \left(-x\right)+\sin \left(-x\right)\)

    28. \(\cos \left(-x\right)+\tan \left(-x\right)\sin \left(-x\right)\)

    Answer

    1. II

    3. I

    5. Period: \(\dfrac{\pi}{4}\). Horizontal shift: 8 right

    7. Period: 8. Horizontal shift: 1 left

    9. Period: 6. Horizontal shift: 3 left

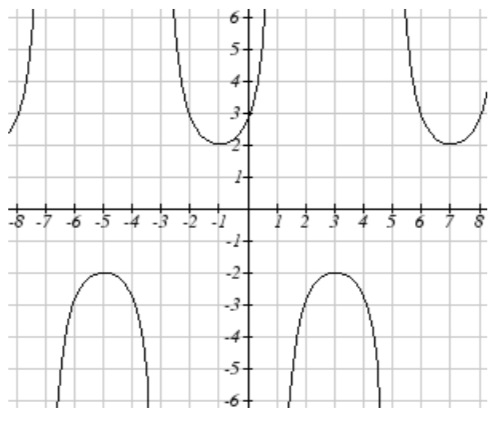
    11. Screen Shot 2019-10-11 at 1.59.39 PM.png

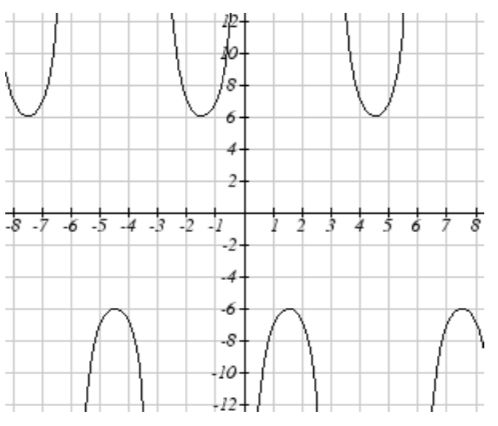
    13. Screen Shot 2019-10-11 at 2.00.14 PM.png

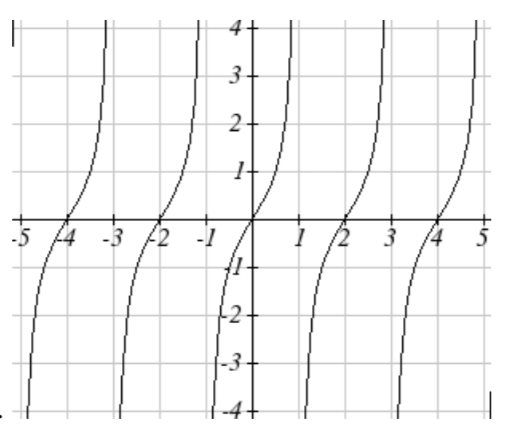
    15. Screen Shot 2019-10-11 at 2.01.07 PM.png

    17. \(f(x) = 2 \sec(\dfrac{\pi}{2} x) - 1\)

    19. \(f(x) = 2 \csc(\dfrac{\pi}{4} x ) + 1\)

    21. \(\tan(-x) = 1.5\)

    23. \(\sec(-x) = 2\)

    25. \(\csc(-x) = 5\)

    27. \(-\csc(x)\)