1.5.1: Transformation of Functions

Last updated
Save as PDF

Page ID: 30242

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Section 1.5 Exercises

Describe how each function is a transformation of the original function $f(x)$

1. $f(x - 49)$

2. $f(x + 43)$

3. $f(x+3)$

4. $f(x-4)$

5. $f(x)+5$

6. $f(x)+8$

7. $f(x)-2$

8. $f(x)-7$

9. $f(x-2)+3$

10. $f(x+4)-1$

11. Write a formula for $f(x)=\sqrt{x}$ shifted up 1 unit and left 2 units.

12. Write a formula for $f(x)=|x|$ shifted down 3 units and right 1 unit.

13. Write a formula for $f(x)=\dfrac{1}{x}$ shifted down 4 units and right 3 units.

14. Write a formula for $\; f(x)=\dfrac{1}{x^{2} }$ shifted up 2 units and left 4 units.

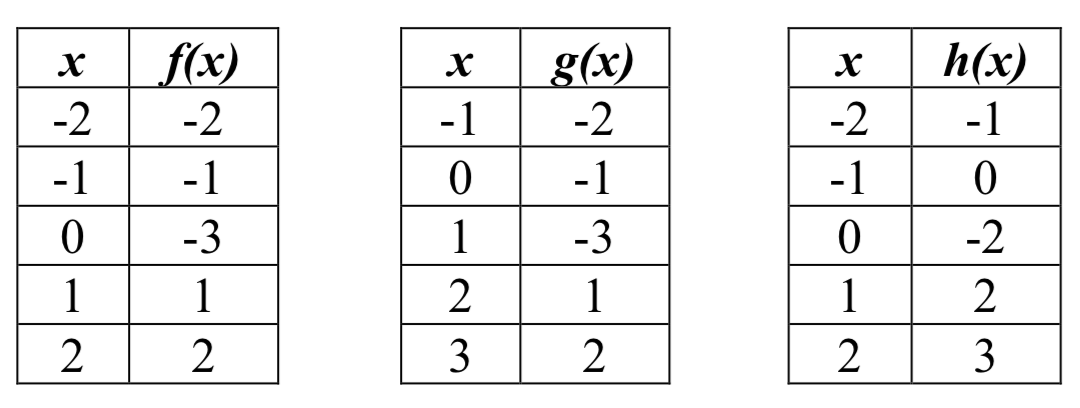
15. Tables of values for $f(x)$, $g(x)$, and $h(x)$ are given below. Write $g(x)$ and $h(x)$ as transformations of $f(x)$.

$屏幕快照 2019-06-14 下午3.07.52.png$

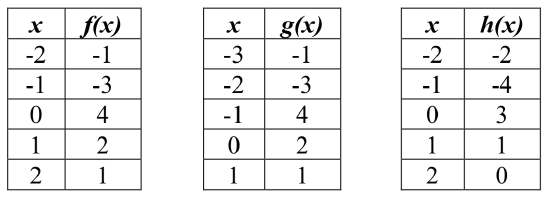
16. Tables of values for $f(x)$, $g(x)$, and $h(x)$ are given below. Write $g(x)$ and $h(x)$ as transformations of $f(x)$.

$屏幕快照 2019-06-14 下午3.08.46.png$

The graph of $f(x)=2^{x}$ is shown. Sketch a graph of each transformation of $f(x)$.

17. $g(x)=2^{x} +1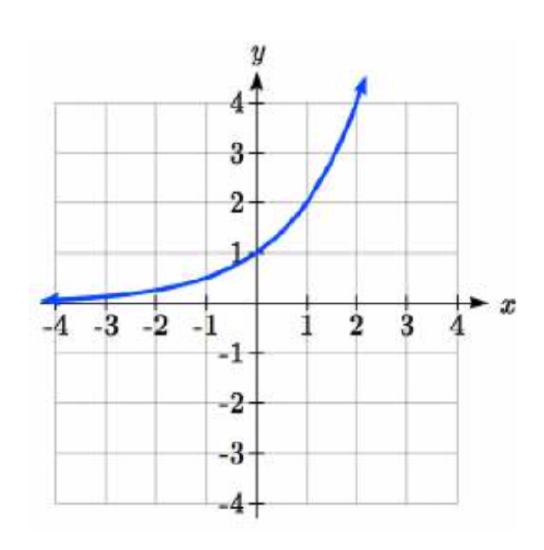$ $屏幕快照 2019-06-14 下午3.10.53.png$

18. $h(x)=2^{x} -3$

19. $w(x)=2^{x-1}$

20. $q(x)=2^{x+3}$

Sketch a graph of each function as a transformation of a toolkit function.

21. $f(t)=(t+1)^{2} -3$

22. $h(x)=|x-1|+4$

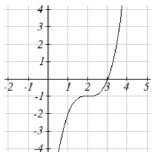
23. $k(x=(x-2)^{3} -1$

24. $m(t)=3+\sqrt{t+2}$

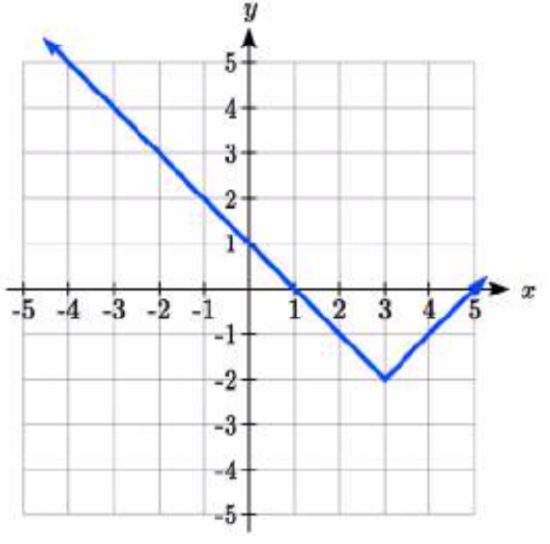
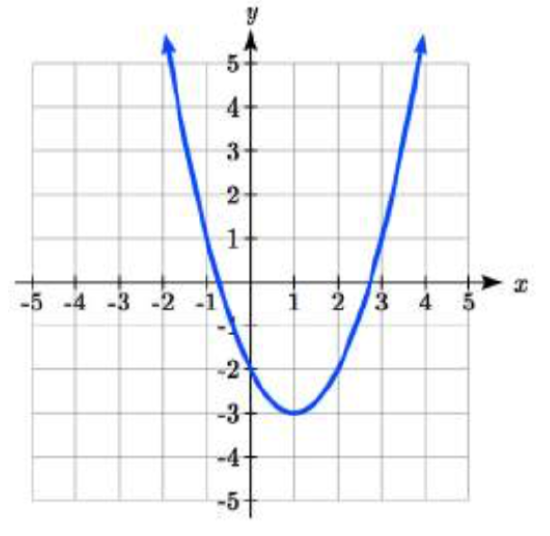
Write an equation for each function graphed below.

25. $屏幕快照 2019-06-14 下午3.13.43.png$

26. $屏幕快照 2019-06-14 下午3.14.17.png$

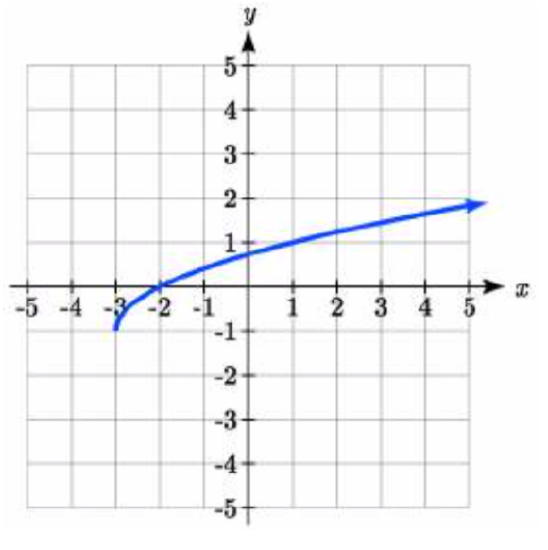
27. $屏幕快照 2019-06-14 下午3.14.58.png$

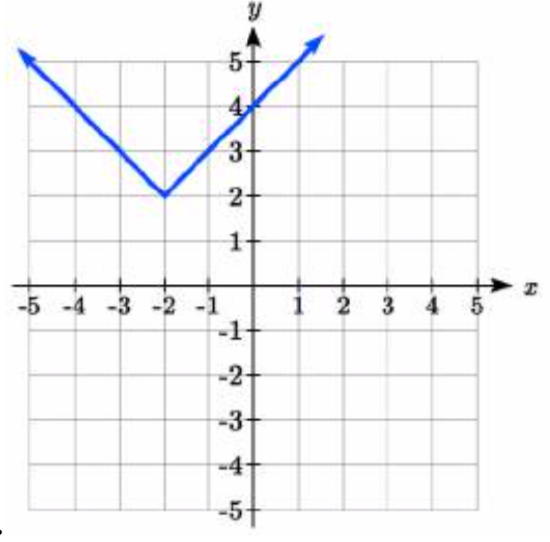
28. $屏幕快照 2019-06-14 下午3.15.37.png$

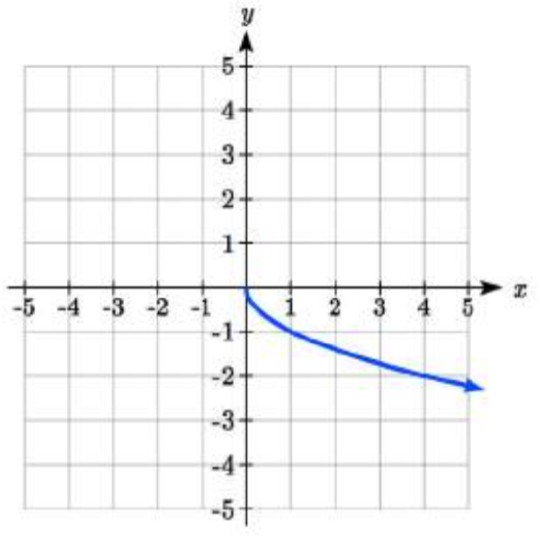
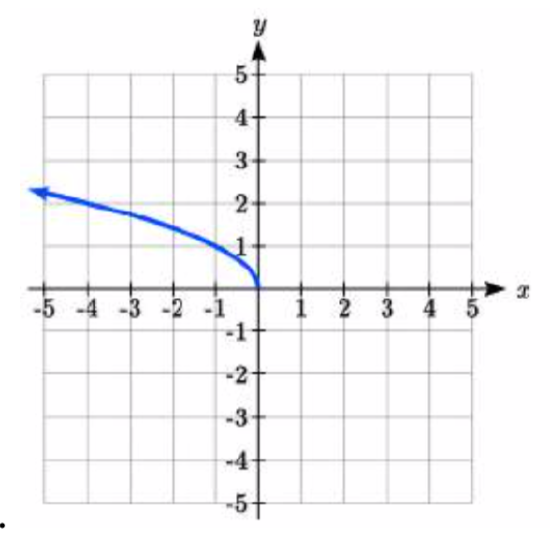
Find a formula for each of the transformations of the square root whose graphs are given below.

29. $屏幕快照 2019-06-14 下午3.16.39.png$

30. $屏幕快照 2019-06-14 下午3.17.08.png$

The graph of $f(x)=2^{x}$ is shown. Sketch a graph of each transformation of $f(x)$

$屏幕快照 2019-06-14 下午3.18.02.png$

31. $g(x)=-2^{x} +1$

32. $h(x)=2^{-x}$

33. Starting with the graph of $f(x)= 6^{x}$ write the equation of the graph that results from

a. reflecting $f(x)$ about the $x$-axis and the $y$-axis

b. reflecting $f(x)$ about the $x$-axis, shifting left 2 units, and down 3 units

34. Starting with the graph of $f(x)= 4^{x}$ write the equation of the graph that results from

a. reflecting $f(x)$ about the $x$-axis

b. reflecting $f(x)$ about the $y$-axis, shifting right 4 units, and up 2 units

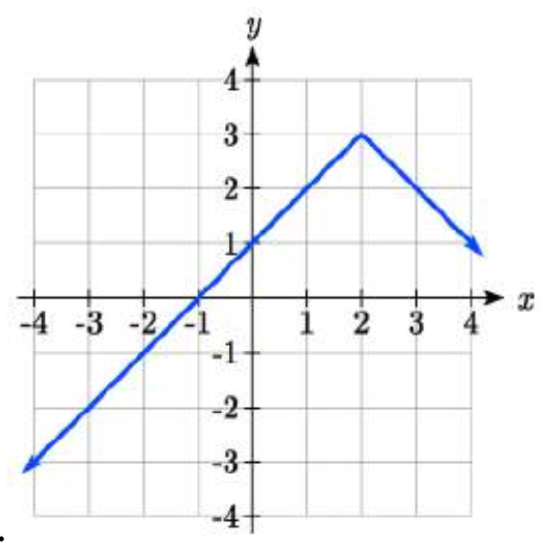
Write an equation for each function graphed below.

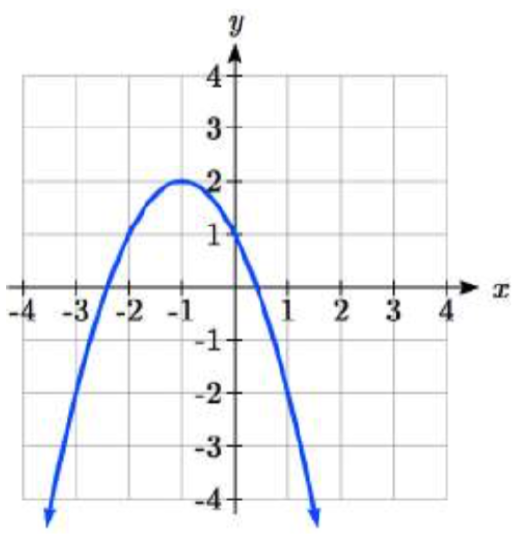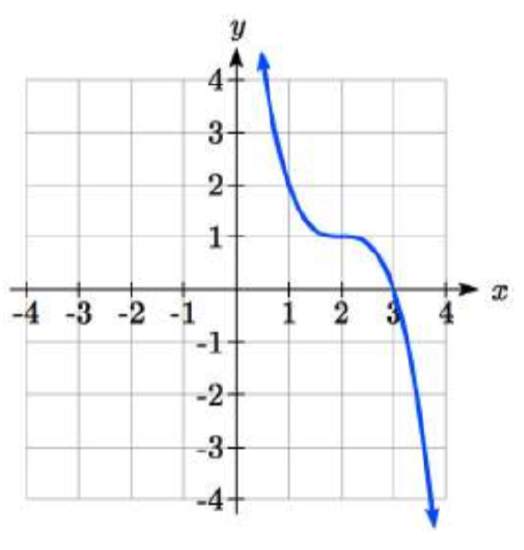
35. $屏幕快照 2019-06-14 下午3.21.50.png$ 36. $屏幕快照 2019-06-14 下午3.22.23.png$

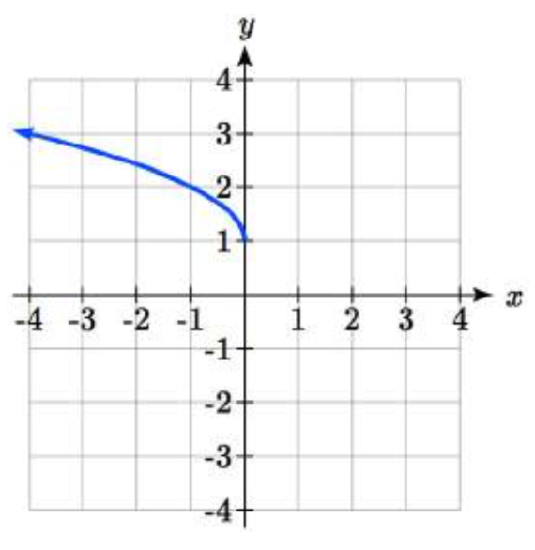37. $屏幕快照 2019-06-14 下午3.23.15.png$ 38. $屏幕快照 2019-06-14 下午3.23.48.png$

39. For each equation below, determine if the function is Odd, Even, or Neither.

a. $f(x)=3 x^{4}$

b. $g(x)=\sqrt{x}$

c. $h(x)=\dfrac{1}{x} +3 x$

40. For each equation below, determine if the function is Odd, Even, or Neither.

a. $f(x)=(x-2)^{2}$

b. $g(x)=2 x^{4}$

c. $h(x)=2 x-x^{3}$

Describe how each function is a transformation of the original function $f(x)$.

41. $-f(x)$

42. $f(-x)$

43. $4f(x)$

44. $6f(x)$

45. $f(5x)$

46. $f(2x)$

47. $f(\dfrac{1}{3} x)$

48. $f(\dfrac{1}{5} x)$

49. $3f(-x)$

50. $-f(3x)$

Write a formula for the function that results when the given toolkit function is transformed as described.

51. $f(x)=|x|$ reflected over the y axis and horizontally compressed by a factor of $\dfrac{1}{4}$.

52. $f(x)=\sqrt{x}$ reflected over the x axis and horizontally stretched by a factor of 2.

53. $f(x)=\dfrac{1}{x^{2} }$ vertically compressed by a factor of $\dfrac{1}{3}$, then shifted to the left 2 units and down 3 units.

54. $f(x)=\dfrac{1}{x}$ vertically stretched by a factor of 8, then shifted to the right 4 units and up 2 units.

55. $f(x)=x^{2}$ horizontally compressed by a factor of $\dfrac{1}{2}$, then shifted to the right 5 units and up 1 unit.

56. $f(x)=x^{2}$ horizontally stretched by a factor of 3, then shifted to the left 4 units and down 3 units.

Describe how each formula is a transformation of a toolkit function. Then sketch a graph of the transformation.

57. $f\left(x\right)=4(x+1)^{2} -5$

58. $g(x)=5(x+3)^{2} -2$

59. $h(x)=-2|x-4|+3$

60. $k(x)=-3\sqrt{x} -1$

61. $m(x)=\dfrac{1}{2} x^{3}$

62. $n(x)=\dfrac{1}{3} |x-2|$

63. $p(x)=(\dfrac{1}{3} x)^{2} -3$

64. $q(x)=(\dfrac{1}{4} x)^{3} +1$

65. $a(x)=\sqrt{-x+4}$

66. $b(x)=\sqrt[{3}]{-x-6}$

Determine the interval(s) on which the function is increasing and decreasing.

67. $f(x)=4(x+1)^{2} -5$

68. $g(x)=5(x+3)^{2} -2$

69. $a(x)=\sqrt{-x+4}$

70. $k(x)=-3\sqrt{x} -1$

Determine the interval(s) on which the function is concave up and concave down.

71. $m(x)=-2(x+3)^{3} +1$

72. $b(x)=\sqrt[{3}]{-x-6}$

73. $p(x)=(\dfrac{1}{3} x)^{2} -3$

74. $k(x)=-3\sqrt{x} -1$

The function $f(x)$ is graphed here. Write an equation for each graph below as a transformation of $f(x)$.

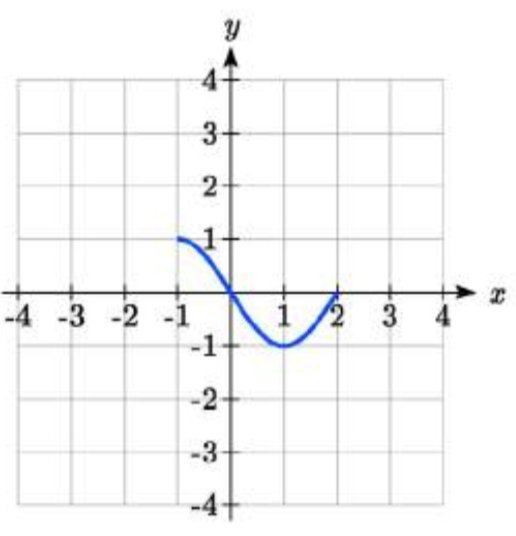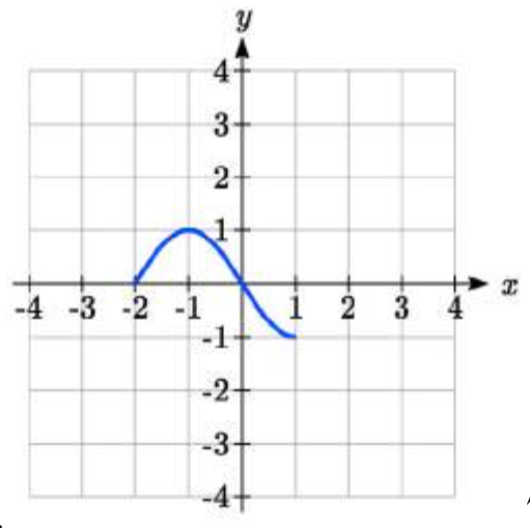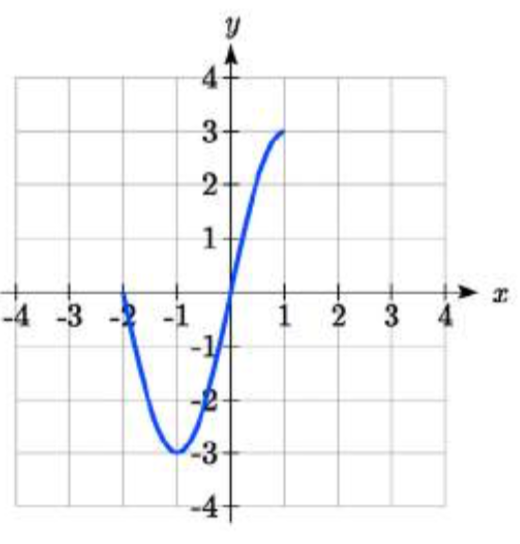
75. $屏幕快照 2019-06-14 下午3.38.50.png$ 76. $屏幕快照 2019-06-14 下午3.39.25.png$ 77. $屏幕快照 2019-06-14 下午3.40.01.png$

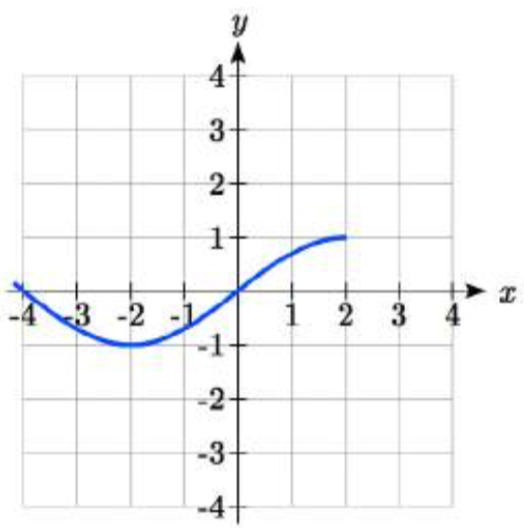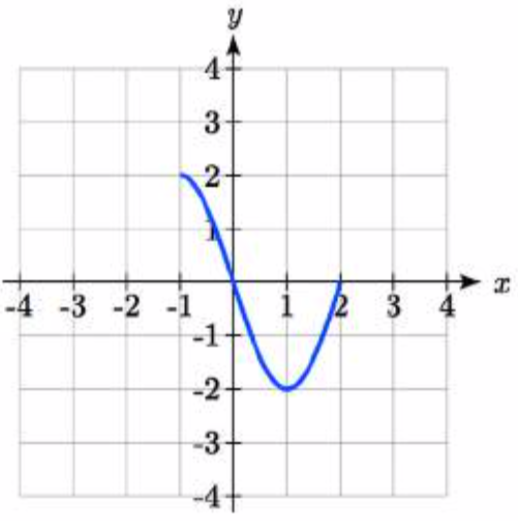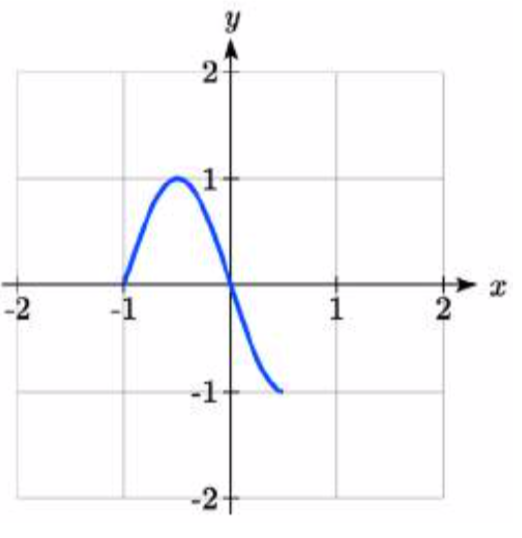
78. $屏幕快照 2019-06-14 下午3.40.25.png$ 79. $屏幕快照 2019-06-14 下午3.41.11.png$ 80. $屏幕快照 2019-06-14 下午3.41.43.png$

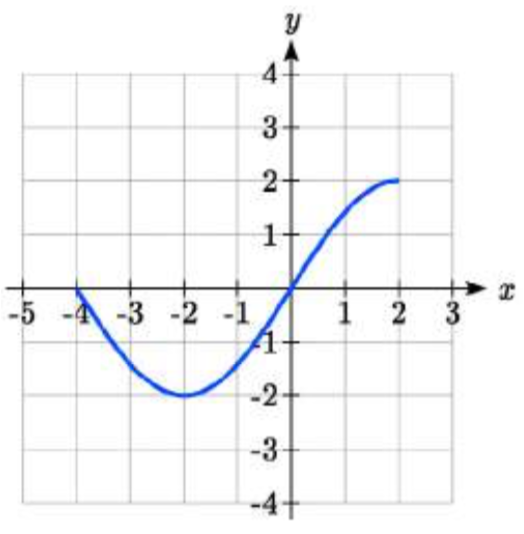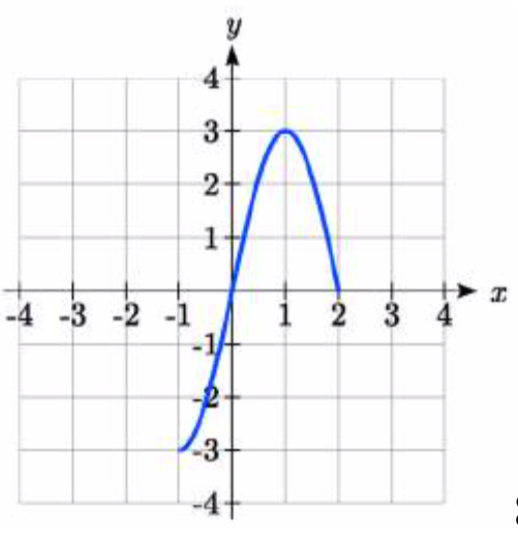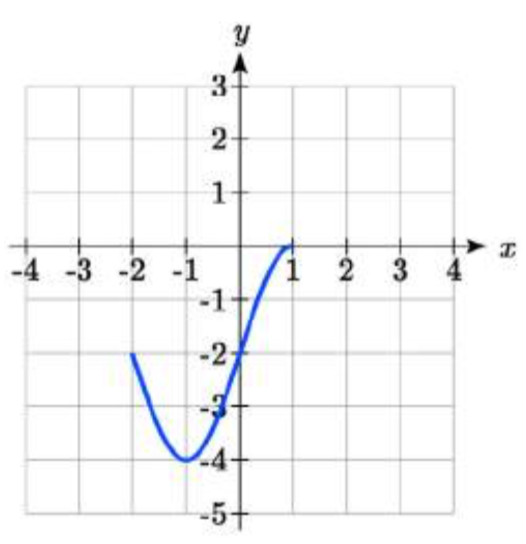
81. $屏幕快照 2019-06-14 下午3.42.36.png$ 82. $屏幕快照 2019-06-14 下午3.43.25.png$ 83. $屏幕快照 2019-06-14 下午3.43.59.png$

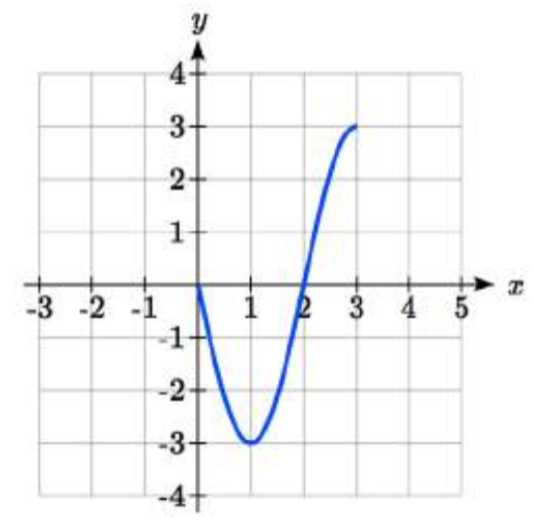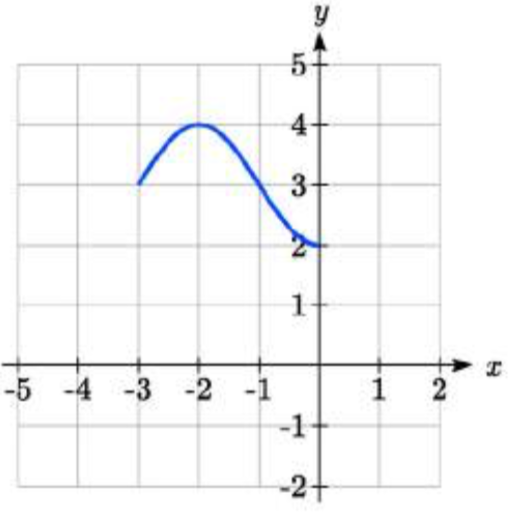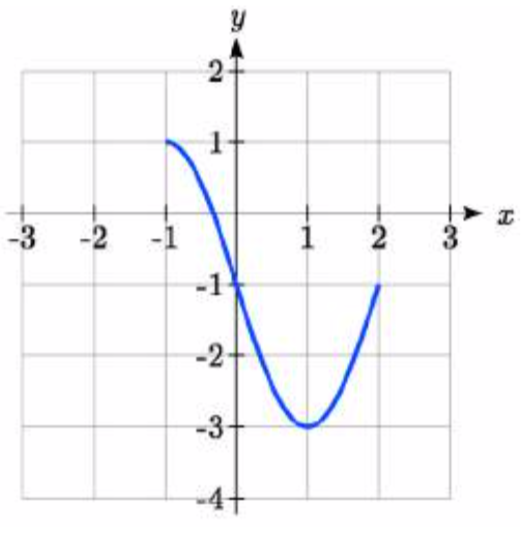
84. $屏幕快照 2019-06-14 下午3.44.41.png$ 85. $屏幕快照 2019-06-14 下午3.45.12.png$ 86. $屏幕快照 2019-06-14 下午3.45.47.png$

Write an equation for each transformed toolkit function graphed below.

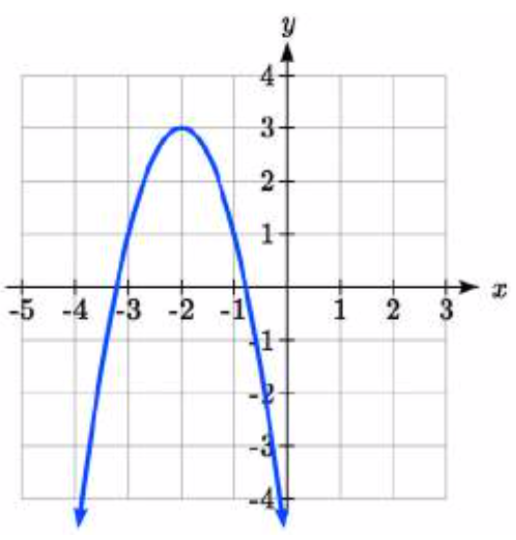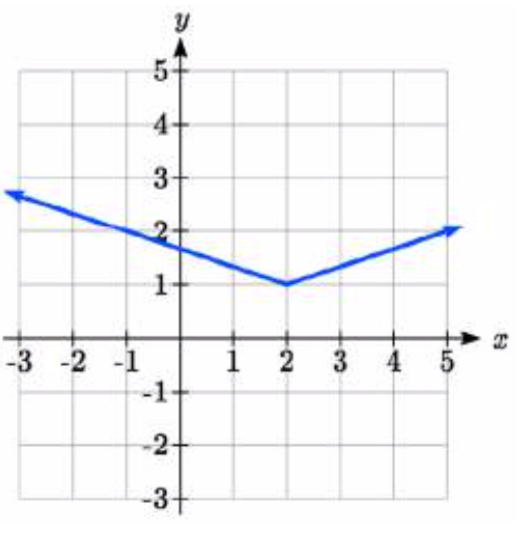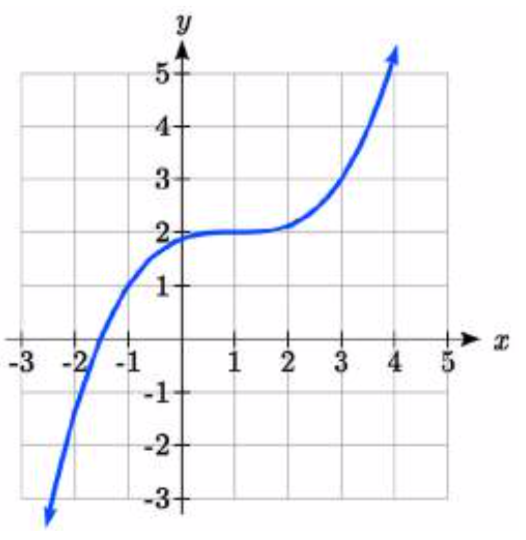
87. $屏幕快照 2019-06-14 下午3.47.01.png$ 88. $屏幕快照 2019-06-14 下午3.47.33.png$ 89. $屏幕快照 2019-06-14 下午3.47.59.png$

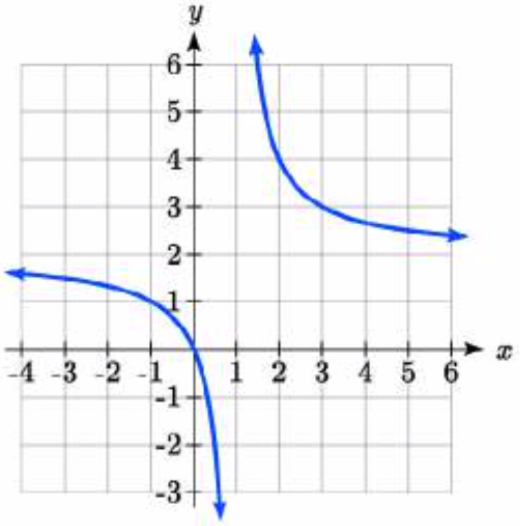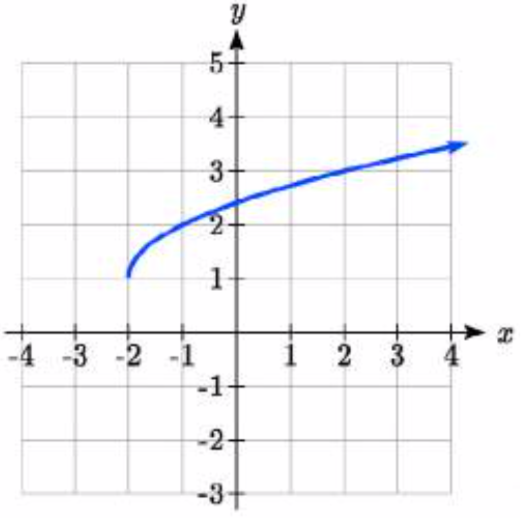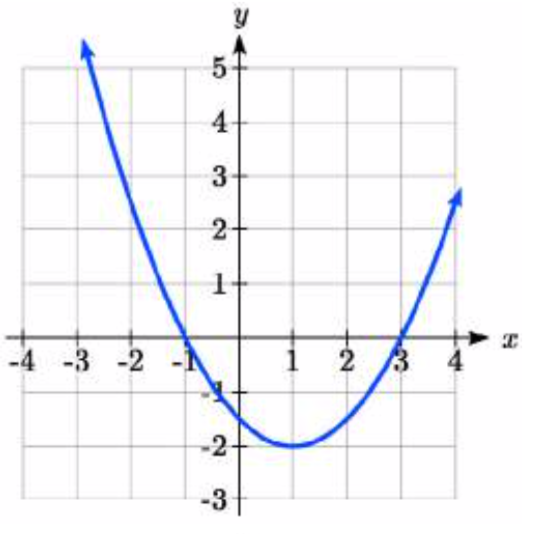
90. $屏幕快照 2019-06-14 下午3.48.35.png$ 91. $屏幕快照 2019-06-14 下午3.49.16.png$ 92. $屏幕快照 2019-06-14 下午3.49.47.png$

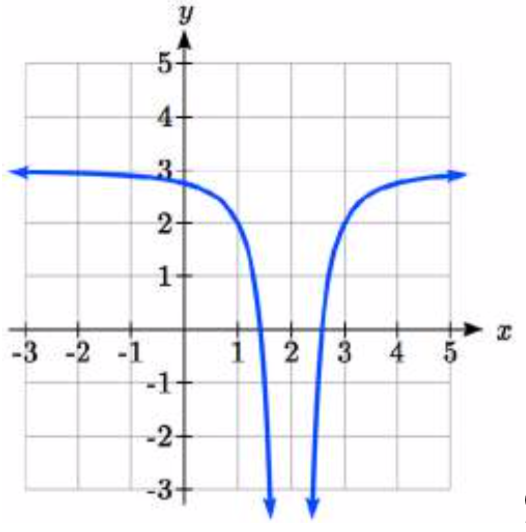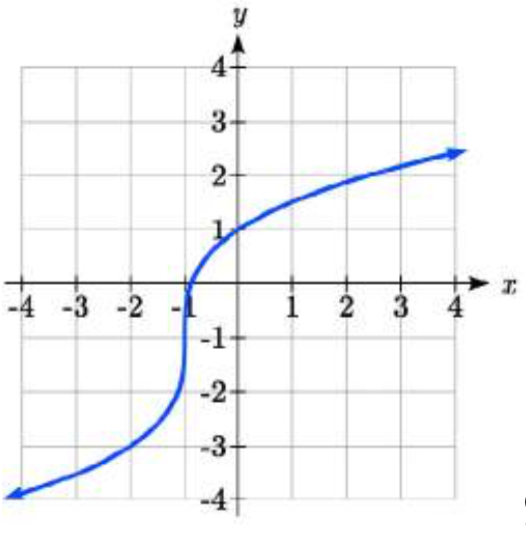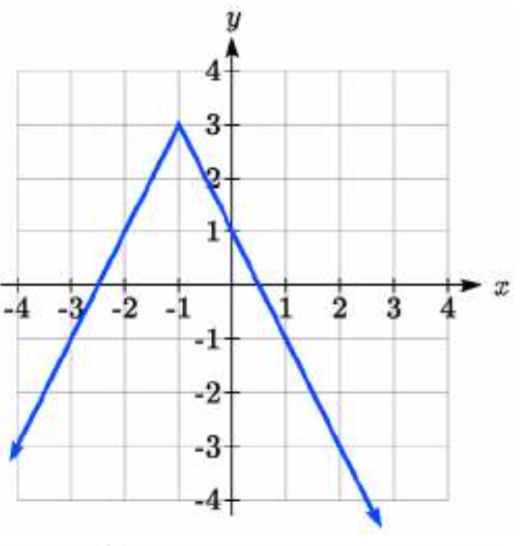
93. $屏幕快照 2019-06-14 下午3.53.14.png$ 94. $屏幕快照 2019-06-14 下午3.53.57.png$ 95. $屏幕快照 2019-06-14 下午3.54.44.png$

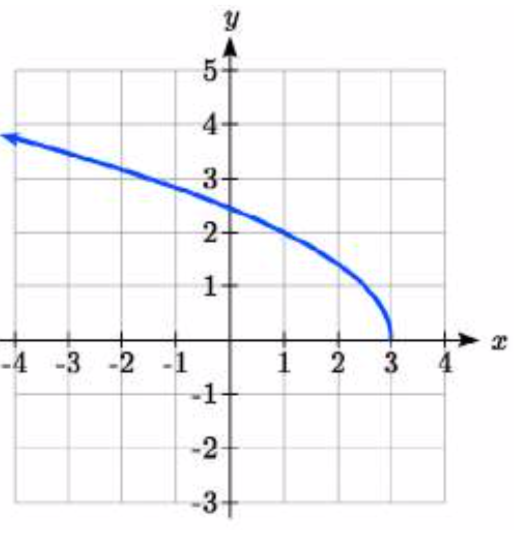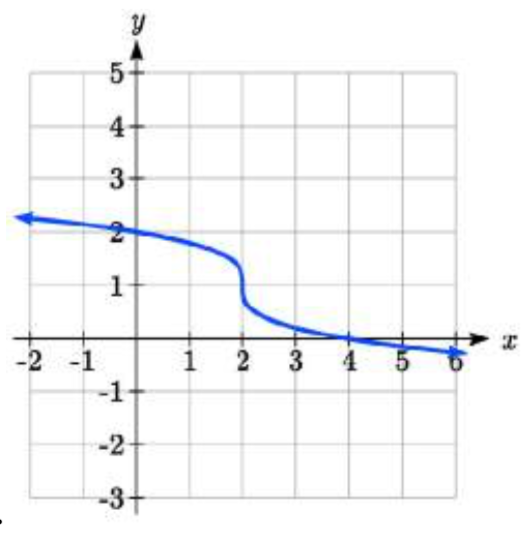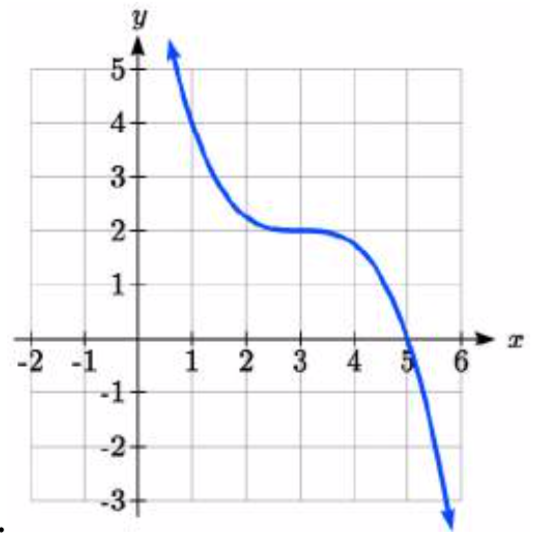
96. $屏幕快照 2019-06-14 下午3.55.27.png$ 97. $屏幕快照 2019-06-14 下午3.57.57.png$ 98. $屏幕快照 2019-06-14 下午3.59.00.png$

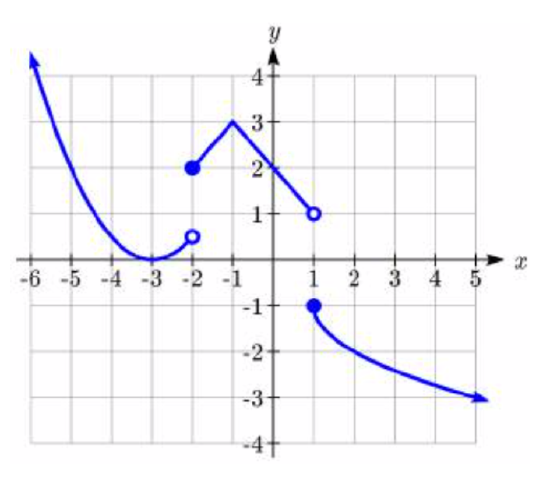
Write a formula for the piecewise function graphed below.

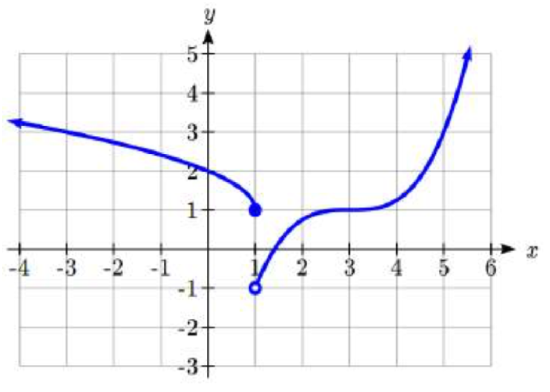
99. 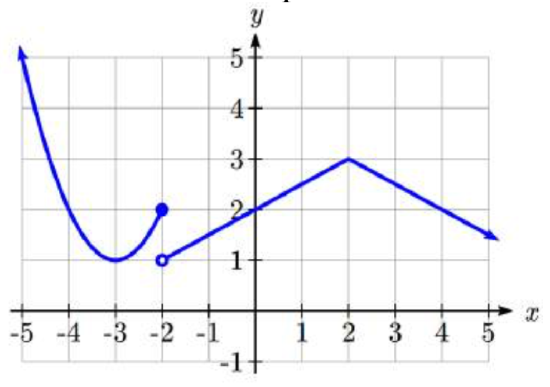$屏幕快照 2019-06-14 下午3.59.40.png$ 100. $屏幕快照 2019-06-14 下午4.00.25.png$

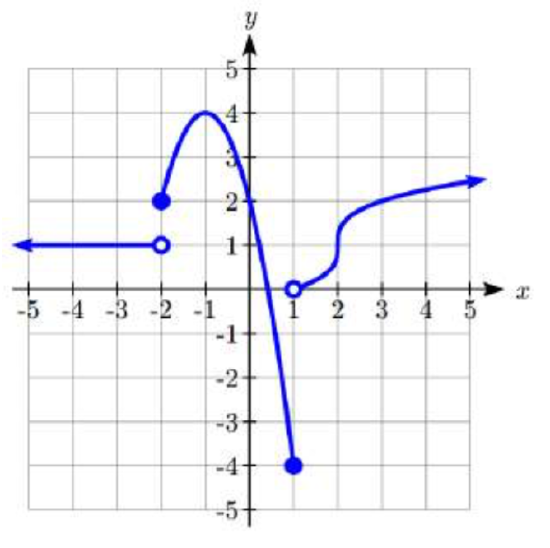101. $屏幕快照 2019-06-14 下午4.01.04.png$ 102. $屏幕快照 2019-06-14 下午4.01.26.png$

103. Suppose you have a function $y = f(x)$ such that the domain of $f(x)$ is $1 \le x \le 6$ and the range of $f(x)$ is (-3 \le y \le 5\). [UW]

a. What is the domain of $\; f(2(x-3))\;$?

b. What is the range of $f(2(x-3))$ ?

c. What is the domain of $2f(x)-3$ ?

d. What is the range of $2f(x)-3$ ?

e. Can you find constants $B$ and $C$ so that the domain of $f(B(x-C))$ is $8 \le x \le 9$?

f. Can you find constants $A$ and $D$ so that the range of $Af(x) + D$ is 0 $0 \le y \le 1$?

Answer

1. Horizontal shift right 49 units

3. Horizontal shift left 3 units

5. Vertical shift up 5 units

7. Vertical shift down 2 units

9. Horizontal shift right 2 units, Vertical shift up 3 units

11. $f(x + 2) + 1 = \sqrt{x + 2} + 1$

13. $f(x - 3) - 4 = \dfrac{1}{x - 3} - 4$

15. $g(x) = f(x - 1)$, $h(x) = f(x) + 1$

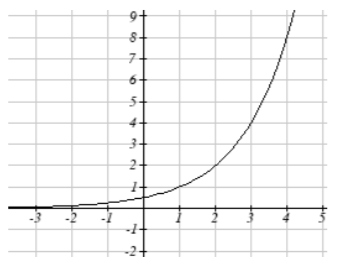
17. 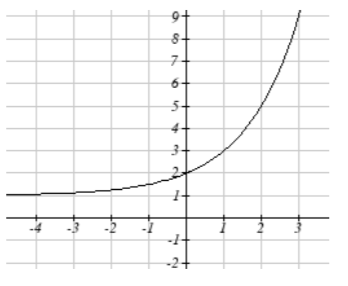$Screen Shot 2019-10-01 at 8.56.34 AM.png$ 19. $Screen Shot 2019-10-01 at 8.56.55 AM.png$

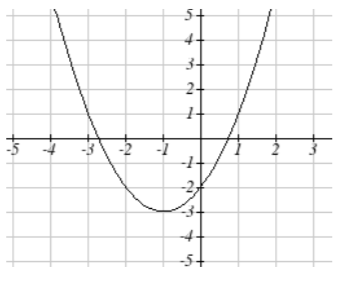21. $Screen Shot 2019-10-01 at 8.57.26 AM.png$ 23. $Screen Shot 2019-10-01 at 8.57.54 AM.png$

25. $y = |x - 3| - 2$

27. $y = \sqrt{x + 3} - 1$

29. $y = -\sqrt{x}$

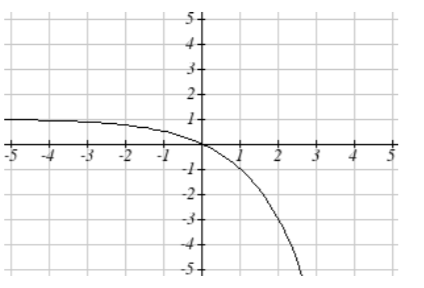
31. $Screen Shot 2019-10-01 at 8.58.26 AM.png$

33. a. $-f(-x) = -6^{-x}$
b. $-f(x + 2) - 3 = -6^{x + 2} - 3$

35. $y = -(x + 1)^2 + 2$

37. $y = \sqrt{-x} + 1$

39. a. Even
b. Neither
c. Odd

41. Reflect $f(x)$ about the $x$-axis

43. Vertically stretch $y$ values by 4

45. Horizontally compress $x$ values by 1/5

47. Horizontally stretch $x$ values by 3

49. Reflect $f(x)$ about the $y$-axis and vertically stretch $y$ values by 3

51. $f(-4x) = |-4x|$

53. $\dfrac{1}{3} f(x + 2) - 3 = \dfrac{1}{3(x + 2)^2} - 3$

55. $f(2(x - 5)) + 1 = (2 (x - 5))^2 + 1$

57. Horizontal shift left 1 unit, vertical stretch $y$ values by 4, vertical shift down 5 units

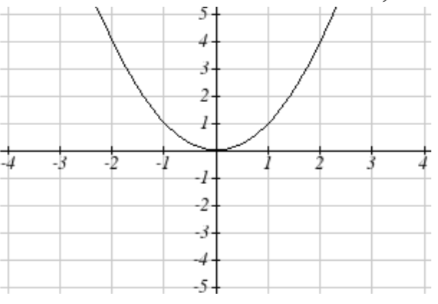$Screen Shot 2019-10-01 at 9.00.14 AM.png$ becomes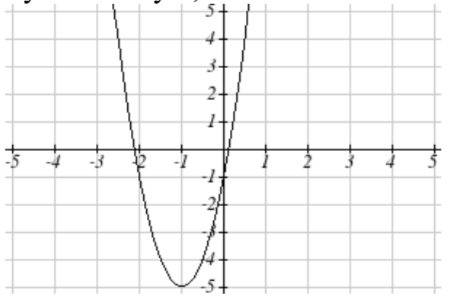 $Screen Shot 2019-10-01 at 9.00.39 AM.png$

59. Horizontal shift right 4 units, vertical stretch $y$ values by 2, reflect over $x$ axis, vertically shift up 3 units.

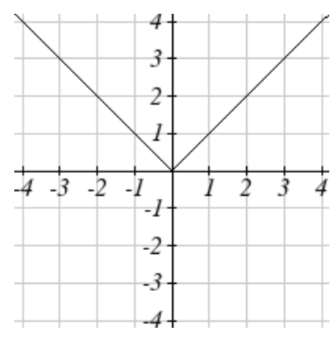$Screen Shot 2019-10-01 at 9.01.08 AM.png$ becomes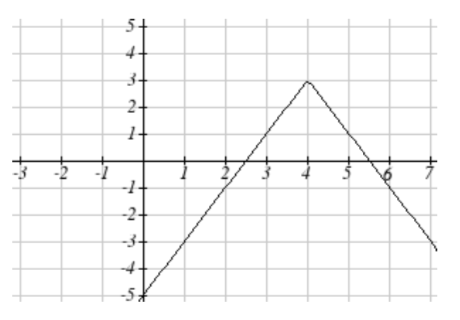 $Screen Shot 2019-10-01 at 9.01.37 AM.png$

61. Vertically compress $y$ values by 1/2

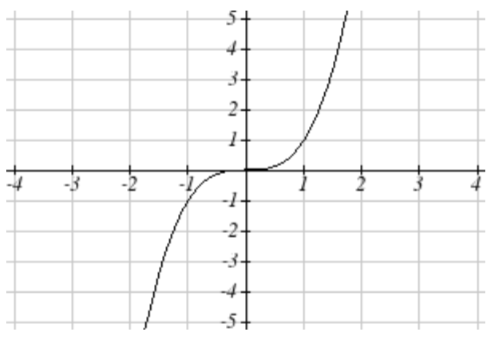$Screen Shot 2019-10-01 at 9.06.17 AM.png$ becomes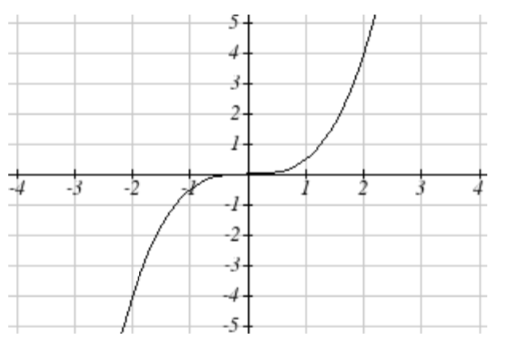 $Screen Shot 2019-10-01 at 9.06.43 AM.png$

63. Horizontally stretch $x$ values by 3, vertical shift down 3 units

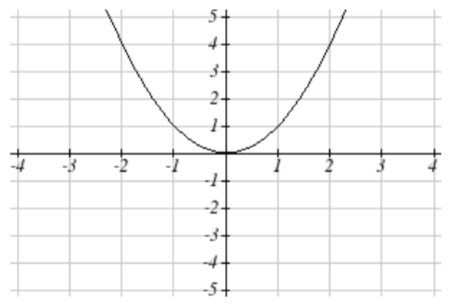$Screen Shot 2019-10-01 at 9.07.21 AM.png$ becomes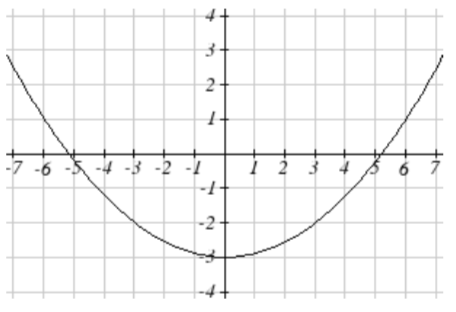 $Screen Shot 2019-10-01 at 9.07.43 AM.png$

65. Reflected over the $y$ axis, horizontally shift right 4 units $a(x) = \sqrt{-(x - 4)}$

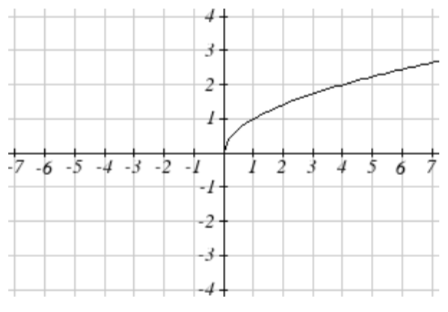$Screen Shot 2019-10-01 at 9.08.13 AM.png$ becomes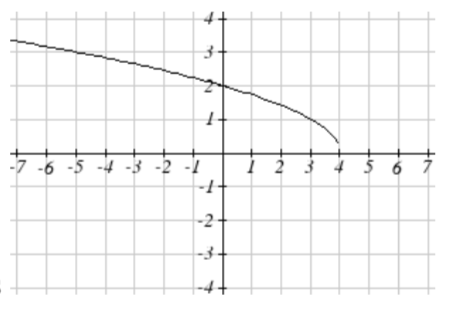 $Screen Shot 2019-10-01 at 9.08.42 AM.png$

67. This function is increasing on $(-1, \infty)$ and decreasing on $(-\infty, -1)$

69. This function is decreasing on $(-\infty, 4)$

71. This function is concave down on $(-3, \infty)$ and concave up on $(-\infty, -3)$

73. This function is concave up everywhere

75. $f(-x)$

77. $3f(x)$

79. 2$f(-x)$

81. $2f(\dfrac{1}{2}x)$

83. $2f(x) - 2$

85. $-f(x + 1) + 3$

87. $y = -2(x + 2)^2 + 3$

89. $y = (\dfrac{1}{2} (x - 1))^3 + 2$

91. $y = \sqrt{2(x + 2)} + 1$

93. $y = \dfrac{-1}{(x - 2)^2} + 3$

95. $y = -2|x + 1| + 3$

97. $y = \sqrt[3]{-\dfrac{1}{2}(x - 2)} + 1$

99. $f(x) = \begin{cases} (x+3)^2 + 1 & if & x \le -2 \\ \dfrac{1}{2}|x - 2| + 3 & if & x > -2 \end{cases}$

101. $f(x) = \begin{cases} 1 & if & x < -2 \\ -2(x + 1)^2 + 4 & if & -2 \le x \le 1 \\ \sqrt[3]{x - 2} + 1 & if & x > 1 \end{cases}$

103a. Domain: $3.5 \le x \le 6$
d. Range: $-9 \le y \le 7$