1.E: The Trigonometric Functions (Exercises)
- Page ID
- 17332
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercise \(\PageIndex{1}\)
The following diagram shows eight points plotted on the unit circle. These points correspond to the following values when the number line is wrapped around the unit circle.
\(t = 1, t = 2, t = 3, t = 4, t = 5, t = 6, t = 7\), and \(t = 9\).
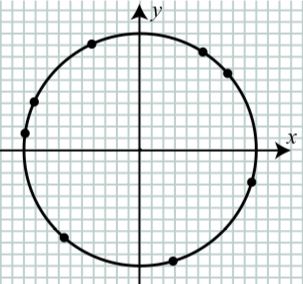
Figure \(\PageIndex{1}\)
(a) Label each point in the diagram with its value of \(t\).
(b) Approximate the coordinates of the points corresponding to \(t = 1, t = 5\), and \(t=9\).
- Answer
-
\(t\) point \(1\) \((0.54, 0.84)\) \(5\) \((0.28, -0.96)\) \(9\) \((-0.91, 0.41)\)
Exercise \(\PageIndex{2}\)
The following diagram shows the points corresponding to \(t = \dfrac{\pi}{5}\) and \(t = \dfrac{2\pi}{5}\) when the number line is wrapped around the unit circle.
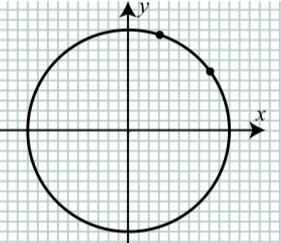
Figure \(\PageIndex{2}\)
On this unit circle, draw the points corresponding to \(t = \dfrac{4\pi}{5}\), \(t = \dfrac{5\pi}{6}\), \(t = \dfrac{8\pi}{5}\) and \(t = \dfrac{10\pi}{5}\).
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{3}\)
Draw the following arcs on the unit circle.
(a) The arc that is determined by the interval \([0, \dfrac{\pi}{6}]\) on the number line.
(b) The arc that is determined by the interval \([0, \dfrac{7\pi}{6}]\) on the number line.
(c) The arc that is determined by the interval \([0, -\dfrac{\pi}{3}]\) on the number line.
(d) The arc that is determined by the interval \([0, -\dfrac{4\pi}{5}]\) on the number line.
- Answer
-
Add texts here. Do not delete this text first.
Exercise \(\PageIndex{4}\)
Determine the quadrant that contains the terminal point of each given arc with initial point \((1, 0)\) on the unit circle.
(a) \(\dfrac{7\pi}{4}\)
(b) \(\dfrac{-7\pi}{4}\)
(c) \(\dfrac{5\pi}{3}\)
(d)\(\dfrac{-5\pi}{3}\)
(e)\(\dfrac{7\pi}{3}\)
(f)\(\dfrac{-7\pi}{3}\)
(g)\(\dfrac{5\pi}{8}\)
(h) \(\dfrac{-5\pi}{8}\)
(i)\(2.5\)
(j)\(-2.5\)
(k) \(3\) (l)\(3+2\pi\)
(m)\(3-\pi\)
(n) \(3-2\pi\)
- Answer
-
\((a)\) \((b)\) \((d)\) \((i)\) \((j)\) \((l)\) \((m)\) \(t\) \(\dfrac{7\pi}{4}\) \(-\dfrac{7\pi}{4}\) \(-\dfrac{3\pi}{5}\) \(2.5\) \(-2.5\) \(3 + 2\pi\) \(3 - \pi\) Quadrant IV I III II III II IV
Exercise \(\PageIndex{5}\)
Find all the points on the unit circle:
(a) Whose x-coordinate is \(\dfrac{1}{3}\)
(b) Whose y-coordinate is \(-\dfrac{1}{2}\)
(c) Whose x-coordinate is \(-\dfrac{3}{5}\)
(d) Whose y-coordinate is \(-\dfrac{3}{4}\) and whose \(x\)-coordinate is negative.
Add text here. For the automatic number to work, you need to add the "AutoNum" template (preferably at the end) to the page.
- Answer
-
(a) We substitute \(x = \dfrac{1}{3}\) into the equation \(x^{2} + y^{2} = 1\). Solving for \(y\), we obtain \(y = \pm\dfrac{\sqrt{8}}{3}\). So the points are \((\dfrac{1}{3}, \dfrac{\sqrt{8}}{3})\) and \((\dfrac{1}{3}, -\dfrac{\sqrt{8}}{3})\).
(b) We substitute \(y = -\dfrac{1}{2}\) into the equation \(x^{2} + y^{2} = 1\). Solving for \(x\), we obtain \(x = \pm\dfrac{\sqrt{3}}{3}\). So the points are \((\dfrac{\sqrt{8}}{3}, -\dfrac{1}{3})\) and \((-\dfrac{\sqrt{3}}{3}, -\dfrac{1}{2})\).
Exercise \(\PageIndex{6}\)
Fill in the blanks for each of the following:
- For a real number \(t\), the value of \(\cos(t)\) is defined to be the ( ) - coordinate of the ( ) point of an arc t whose initial point is ( ) on the ( ) whose equation is \(x^2 + y^2 = 1\).
- The domain of the cosine function is ( ).
- The maximum value of \(\cos(t)\) is ( ) and this occurs at \(t\) = ( ) for \(0 \leq t < 2\pi\). The minimum value of \(\cos(t)\) is ( ) and this occurs at \(t\) = ( ) for \(0 \leq t < 2\pi\).
- The range of the cosine function is ( ).
- Answer
-
1. For a real number \(t\), the value of \(\cos(t)\) is defined to be the x -coordinate of the terminal point of an arc \(t\) whose initial point is \((1, 0)\) on the unit circle whose equation is \(x^{2} + y^{2} = 1\).
2. The domain of the cosine function is the set of all real numbers.
3. The maximum value of \(\cos(t)\) is 1 and this occurs at \(t =\) 0 for \(1 \leq t < 2\pi\). The minimum value of \(\cos(t)\) is -1 and this occurs at \(t = \pi\) for \(0 \leq t < 2\pi\).
4. The range of the cosine function is the closed interval \([-1,1]\).
Exercise \(\PageIndex{7}\)
Fill in the blanks for each of the following:
- For a real number \(t\), the value of sin\((t)\) is defined to be the ( ) - coordinate of the ( ) point of an arc t whose initial point is ( ) on the ( ) whose equation is \(x^2 + y^2 = 1\).
- The domain of the sine function is ( ).
- The maximum value of \(\sin(t)\) is ( ) and this occurs at \(t\) = ( ) for \(0 \leq t < 2\pi\). The minimum value of \(\sin(t)\) is ( ) and this occurs at \(t\) = ( ) for \(0 \leq t < 2\pi\).
- The range of the sine function is ( ).
- Answer
-
(a) \(\cos(t) = \dfrac{4}{5}\) or \(\cos(-\dfrac{4}{5})\).
(c) \(\sin(t) = -\dfrac{-\sqrt{5}}{3}\).
Exercise \(\PageIndex{8}\)
- Complete the following table of values:
|
Length of arc on the unit circle |
Terminal point of the arc |
\(\cos(t)\) |
\(\sin(t)\) |
| \(0\) | \((1, 0)\) | \(1\) | \(0\) |
| \(\dfrac{\pi}{2}\) | |||
| \(\pi\) | |||
| \(\dfrac{3\pi}{2}\) | |||
| \(2\pi\) |
- Complete the following table of values:
|
Length of arc on the unit circle |
Terminal point of the arc |
\(\cos(t)\) |
\(\sin(t)\) |
| \(0\) | \((1, 0)\) | \(1\) | \(0\) |
| \(-\dfrac{\pi}{2}\) | |||
| \(-\pi\) | |||
| \(-\dfrac{3\pi}{2}\) | |||
| \(-2\pi\) |
- Complete the following table of values:
|
Length of arc on the unit circle |
Terminal point of the arc |
\(\cos(t)\) |
\(\sin(t)\) |
| \(2\pi\) | \((1, 0)\) | \(1\) | \(0\) |
| \(\dfrac{5\pi}{2}\) | |||
| \(3\pi\) | |||
| \(\dfrac{7\pi}{2}\) | |||
| \(4\pi\) |
Exercise \(\PageIndex{9}\)
- What are the possible values of \(\cos(t)\) if it is known that \(\sin(t) = \dfrac{3}{5}\)?
- What are the possible values of \(\cos(t)\) if it is known that \(\sin(t) = \dfrac{3}{5}\) and the terminal point of \(t\) is in the second quadrant?
- What is the value of \(\sin(t)\) if it is known that \(\cos(t) = \dfrac{-2}{3}\) and the terminal point of \(t\) is in the third quadrant?
Exercise \(\PageIndex{10}\)
Suppose it is known that \(0 < \cos(t) < \dfrac{1}{3}\).
- By squaring the expressions in the given inequalities, what conclusions can be made about \(\cos^2(t)\)?
- Use part(a) to write inequalities involving \(-\cos^2(t)\) and then inequalities involving \(1 - \cos^2(t)\).
- Using the Pythagorean identity, we see that \(\sin^2(t) = 1 - \cos^2(t)\). Write the last inequality in part (b) in terms of \(\sin^2(t)\).
- If we also know that \(\sin(t) > 0\), what can we now conclude about the value of \(\sin(t)\)?
Answer
(a) \(0 < \cos^{2}(t) < \dfrac{1}{9}\).
(b) \(-\dfrac{1}{9} < -\cos^{2}(t) < 0\) and so \(\dfrac{8}{9} < 1 - \cos^{2}(t) < 1\)
(c) \(\dfrac{8}{9} < \sin^{2}(t) < 1\)
(d) \(\dfrac{\sqrt{8}}{3} < \sin(t) < 1\)
Exercise \(\PageIndex{11}\)
Use a process similar to the one in exercise (5) to complete each of the following:
- Suppose it is known that \(-\dfrac{1}{4} < sin(t) < 0\) and that \(\cos(t) > 0\). What can be concluded about \(\cos(t)\)?
- Suppose it is known that \( 0 \leq \sin(t) \leq \dfrac{3}{7}\) and that \(\cos(t) < 0\). What can be concluded about \(\cos(t)\)?
Exercise \(\PageIndex{12}\)
Using the four digit approximations for the cosine and sine values in Exercise 1.6, calculate each of the following:
- \(\cos^2(1) + \sin^2(1)\)
- \(\cos^2(2) + \sin^2(2)\)
- \(\cos^2(-4) + \sin^2(-4)\)
- \(\cos^2(15) + \sin^2(15)\)
What should be the exact value of each of these computations? Why are the results not equal to this exact value?
Exercise \(\PageIndex{13}\)
Convert each of the following degree measurements for angles into radian measures for the angles. In each case, first write the result as a fractional multiple of \(\pi\) and then use a calculator to obtain a 4 decimal place approximation of the radian measure.
(a) \(15^\circ\) (b) \(58^\circ\) (c) \(112^\circ\) (d) \(210^\circ\) (e) \(-40^\circ\) (f) \(-78^\circ\)
Exercise \(\PageIndex{14}\)
Convert each of the following radian measurements for angles into degree measures for the angles. When necessary, write each result as a 4 decimal place approximation.
(a) \(\dfrac{3}{8}\pi\) radians (b) \(\dfrac{7}{9}\pi\) radians (c) \(-\dfrac{7}{15}\pi\) radians (d) \(1\) radians (e)\(2.4\) radians (f) \(3\) radians
- Answer
-
(a) \(67.5^\circ\)
(b) \(231. 4268^\circ\)
(d) \(57.2958^\circ\)
Exercise \(\PageIndex{15}\)
Draw an angle in standard position of an angle whose radian measure is:
(a) \(\dfrac{1}{4}\pi\) (b) \(\dfrac{1}{3}\pi\) (c)\(\dfrac{2}{3}\pi\) (d) \(\dfrac{5}{4}\pi\) (e)\(-\dfrac{1}{3}\pi\) (f) \(3.4\)
Exercise \(\PageIndex{16}\)
In Exercise 1.16, we used the Geogebra Applet called Terminal Points of Arcs on the Unit Circle to approximate values of the cosine and sine functions. We will now do something similar to approximate the cosine and sine values for angles measured in degrees.
We have seen that the terminal side of an angle in standard position intersects the unit circle in a point. We use the coordinates of this point to determine the cosine and sine of that angle. When the angle is measured in radians, the radian measure of the angle is the same as the arc on the unit circle subtended by the angle. This is not true when the angle is measure in degrees, but we can still use the intersection point to define the cosine and sine of the angle. So if an angle in standard position has degree measurement \(a^\circ\), then we define \(\cos(a^\circ)\) to be the x-coordinate of the point of intersection of the terminal side of that angle and the unit circle. We define \(\sin(a^\circ)\) to be the y-coordinate of the point of intersection of the terminal side of that angle and the unit circle.
We will now use the Geogebra applet Angles and the Unit Circle. A web address for this applet is
For this applet, we control the value of the input \(a^\circ\) with the slider for \(a\). The values of a range from \(-180^\circ\) to \(180^\circ\) in increments of \(5^\circ\). For a given value of \(a^\circ\), an angle in standard position is drawn and the coordinates of the point of intersection of the terminal side of that angle and the unit circle are displayed. Use this applet to approximate values for each of the following:
(a) \(\cos(10^\circ)\) and \(\sin(10^\circ)\)
(b) \(\cos(60^\circ)\) and \(\sin(60^\circ)\)
(c) \(\cos(135^\circ)\) and \(\sin(135^\circ)\)
(d) \(\cos(-10^\circ)\) and \(\sin(-10^\circ)\)
(e) \(\cos(-135^\circ)\) and \(\sin(-135^\circ)\)
(f) \(\cos(85^\circ)\) and \(\sin(85^\circ)\)
- Answer
-
(a) \(\cos(10^\cric) \approx 0.9848, \sin(10^circ) \approx 0.1736\)
(b) \(\cos(-10^\cric) \approx 0.9848, \sin(-10^circ) \approx -0.1736\)
Exercise \(\PageIndex{17}\)
Exercise (4) must be completed before doing this exercise. Put the calculator you are using in Degree mode. Then use the calculator to determine the values of the cosine and sine functions in Exercise (4). Are the values the same? How are they different?
Exercise \(\PageIndex{18}\)
Determine the arc length (to the nearest hundredth of a unit when necessary) for each of the following.
(a) An arc on a circle of radius 6 feet that is intercepted by a central angle of \(\dfrac{2\pi}{3}\) radians. Compare this to one-third of the circumference of the circle.
(b) An arc on a circle of radius 100 miles that is intercepted by a central angle of 2 radians.
(c) An arc on a circle of radius 20 meters that is intercepted by a central angle of \(\dfrac{13\pi}{10}\) radians radians.
(d) An arc on a circle of radius 10 feet that is intercepted by a central angle of 152 degrees.
- Answer
-
(a) The arc length is \(4\pi\) feet, which is equal to \(\dfrac{1}{3}\) of the circumference of the circle.
(b) The arc length is \(200\) miles.
(c) The arc length is \(26\pi\) meters.
Exercise \(\PageIndex{19}\)
In each of the following, when it is possible, determine the exact measure of the central angle in radians. Otherwise, round to the nearest hundredth of a radian.
(a)The central angle that intercepts an arc of length \(3\) feet on a circle of radius \(5\) feet.
(b)The central angle that intercepts an arc of length \(18\) feet on a circle of radius \(5\) feet.
(c)The central angle that intercepts an arc of length \(20\) meters on a circle of radius \(12\) meters.
- Answer
-
(a) \(\theta = \dfrac{3\pi}{5}\) radians.
(b) \(\theta = \dfrac{18}{5}\) radians \(= 3.6\) radians.
Exercise \(\PageIndex{20}\)
In each of the following, when it is possible, determine the exact measure of central the angle in degrees. Otherwise, round to the nearest hundredth of a degree.
(a)The central angle that intercepts an arc of length 3 feet on a circle of radius 5 feet.
(b)The central angle that intercepts an arc of length 18 feet on a circle of radius 5 feet.
(c)The central angle that intercepts an arc of length 20 meters on a circle of radius 12 meters.
(d)The central angle that intercepts an arc of length 5 inches on a circle of radius 5 inches.
(e)The central angle that intercepts an arc of length 12 inches on a circle of radius 5 inches.
- Answer
-
(a) \(\theta = 108^\circ\)
(b) \(\theta = (\dfrac{648}{\pi})^\circ \approx 206.26^\circ\)
Exercise \(\PageIndex{21}\)
Determine the distance (in miles) that the planet Mars travels in one week in its path around the sun. For this problem, assume that Mars completes one complete revolution around the sun in 687 days and that the path of Mars around the sun is a circle with a radius of 227.5 million miles.
Exercise \(\PageIndex{22}\)
Determine the distance (in miles) that the Earth travels in one day in its path around the sun. For this problem, assume that Earth completes one complete revolution around the sun in 365.25 days and that the path of Earth around the sun is a circle with a radius of 92.96 million miles.
Exercise \(\PageIndex{23}\)
A compact disc (CD) has a diameter of 12 centimeters (cm). Suppose that the CD is in a CD-player and is rotating at 225 revolutions per minute. What is the angular velocity of the CD (in radians per second) and what is the linear velocity of a point on the edge of the CD?
Exercise \(\PageIndex{24}\)
A person is riding on a Ferris wheel that takes 28 seconds to make a complete revolution. Her seat is 25 feet from the axle of the wheel.
(a) What is her angular velocity in revolutions per minute? Radians per minute? Degrees per minute?
(b) What is her linear velocity?
(c) Which of the quantities angular velocity and linear velocity change if the person’s seat was 20 feet from the axle instead of 25 feet? Compute the new value for any value that changes. Explain why each value changes or does not change.
Exercise \(\PageIndex{25}\)
A small pulley with a radius of \(3\) inches is connected by a belt to a larger pulley with a radius of \(7.5\) inches (See Figure \(\PageIndex{3}\)). The smaller pulley is connected to a motor that causes it to rotate counterclockwise at a rate of \(120\) rpm (revolutions per minute). Because the two pulleys are connected by the belt, the larger pulley also rotates in the counterclockwise direction.
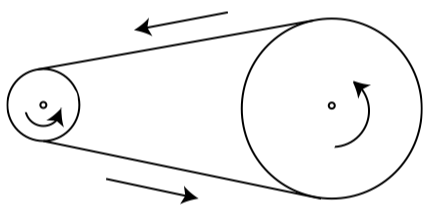
Figure \(\PageIndex{3}\): Two Pulleys Connected by a Belt
(a)Determine the angular velocity of the smaller pulley in radians per minute.
(b)Determine the linear velocity of the rim of the smaller pulley in inches per minute.
(c)What is the linear velocity of the rim of the larger pulley? Explain.
(d)Find the angular velocity of the larger pulley in radians per second.
(e)How many revolutions per minute is the larger pulley turning?
- Answer
-
(b) \(v = 720\pi\dfrac{in}{min} \approx 2261.95\dfrac{in}{min}\)
Exercise \(\PageIndex{26}\)
A small pulley with a radius of \(10\) centimeters inches is connected by a belt to a larger pulley with a radius of \(24\) centimeters inches (See Figure 1.16). The larger pulley is connected to a motor that causes it to rotate counterclockwise at a rate of \(75\) rpm (revolutions per minute). Because the two pulleys are connected by the belt, the smaller pulley also rotates in the counterclockwise direction.
(a)Determine the angular velocity of the larger pulley in radians per minute.
(b)Determine the linear velocity of the rim of the large pulley in inches per minute.
(c)What is the linear velocity of the rim of the smaller pulley? Explain.
(d)Find the angular velocity of the smaller pulley in radians per second.
(e)How many revolutions per minute is the smaller pulley turning?
- Answer
-
(b) \(v = 3600\pi\dfrac{cm}{min} \approx 11309.73\dfrac{cm}{min}\)
Exercise \(\PageIndex{27}\)
The radius of a car wheel is 15 inches. If the car is traveling 60 miles per hour, what is the angular velocity of the wheel in radians per minute? How fast is the wheel spinning in revolutions per minute?
Exercise \(\PageIndex{28}\)
The mean distance from Earth to the moon is 238,857 miles. Assuming the orbit of the moon about Earth is a circle with a radius of 238,857 miles and that the moon makes one revolution about Earth every 27.3 days, determine the linear velocity of the moon in miles per hour. Research the distance of the moon to Earth and explain why the computations that were just made are approximations
Exercise \(\PageIndex{29}\)
A unit circle is shown in each of the following showing information about an arc \(t\). In each case, use the information on the unit circle to determine the values of \(t\), \(\cos(t)\), and \(\sin(t)\).
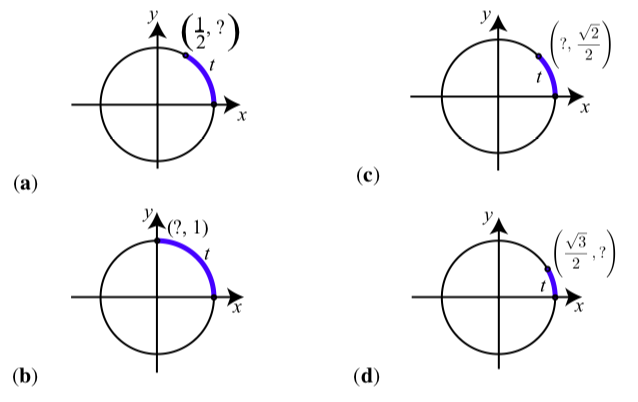
Figure \(\PageIndex{4}\)
- Answer
-
(a) \(t = \dfrac{\pi}{3}, \cos(t) = \dfrac{1}{2}, \sin(t) = \dfrac{\sqrt{3}}{2}\).
(b) \(t = \dfrac{\pi}{2}, \cos(t) = 0, \sin(t) = 1\).
(c) \(t = \dfrac{\pi}{4}, \cos(t) = \dfrac{\sqrt{2}}{2}, \sin(t) = \dfrac{\sqrt{2}}{2}\).
(d) \(t = \dfrac{\pi}{6}, \cos(t) = \dfrac{\sqrt{3}}{2}, \sin(t) = \dfrac{1}{2}\).
Exercise \(\PageIndex{30}\)
Determine the exact value for each of the following expressions and then use a calculator to check the result. For example,
\[\cos(0) + \sin(\dfrac{\pi}{3}) = 1 + \dfrac{\sqrt{3}}{2} \approx 1.8660.\]
(a)\[\cos^2(\dfrac{\pi}{6})\]
(b)\[2\sin^2(\dfrac{\pi}{6}) + \cos(\pi)\]
(c)\[\dfrac{\cos(\dfrac{\pi}{6})}{\sin(\dfrac{\pi}{6})}\]
(d)\[3\sin(\dfrac{\pi}{2}) + \cos(\dfrac{\pi}{4})\]
- Answer
-
(a) \(\cos^{2}(\dfrac{\pi}{6}) = \dfrac{3}{2}\).
(b) \(2\sin^{2}(\dfrac{\pi}{4}) + \cos(\pi) = 0\).
Exercise \(\PageIndex{31}\)
For each of the following, determine the reference arc for the given arc and draw the arc and its reference arc on the unit circle.
(a)\(t = \dfrac{4\pi}{3}\)
(b)\(t = \dfrac{13\pi}{8}\)
(c)\(t = \dfrac{9\pi}{4}\)
(d)\(t = -\dfrac{4\pi}{3}\)
(e)\(t = -\dfrac{7\pi}{5}\) (f)\(t = 5\)
- Answer
-
(a) The reference arc is \(\dfrac{\pi}{3}\).
(b) The reference arc is \(\dfrac{3\pi}{8}\).
(d) The reference arc is \(\dfrac{\pi}{3}\).
Exercise \(\PageIndex{32}\)
For each of the following, draw the given arc t on the unit circle, determine the reference arc for t, and then determine the exact values for \(cos(t)\) and \(sin(t)\).
(a)\(t = \dfrac{5\pi}{6}\)
(b)\(t = \dfrac{5\pi}{4}\)
(c)\(t = \dfrac{5\pi}{3}\)
(d)\(t = -\dfrac{2\pi}{3}\)
(e)\(t = -\dfrac{7\pi}{4}\)
(f)\(t = \dfrac{19\pi}{6}\)
- Answer
-
(a) The reference arc is \(\dfrac{\pi}{6}\); \(\cos(\dfrac{5\pi}{6}) = -\dfrac{\sqrt{3}}{2}\); \(\sin(\dfrac{5\pi}{6}) = -\dfrac{1}{2}\).
(b) The reference arc is \(\dfrac{\pi}{3}\); \(\cos(-\dfrac{2\pi}{3}) = -\dfrac{1}{2}\); \(\sin(-\dfrac{2\pi}{3}) = -\dfrac{\sqrt{3}}{2}\).
Exercise \(\PageIndex{33}\)
(a) Use a calculator (in radian mode) to determine five-digit approximations for \(\cos(4)\) and \(\sin(4)\).
(b) Use a calculator (in radian mode) to determine five-digit approximations for \(\cos(4 - \pi)\) and \(\sin(4 - \pi)\).
(c) Use the concept of reference arcs to explain the results in parts (a) and (b).
Exercise \(\PageIndex{34}\)
Suppose that we have the following information about the arc \(t\).
\[0 < t < \dfrac{\pi}{2} \space and \space sin(t) = \dfrac{1}{5}\]
Use this information to determine the exact values of each of the following:
(a)\(\cos(t)\)
(b)\(\sin(\pi - t)\)
(c)\(\cos(\pi - t)\)
(d)\(\sin(\pi + t)\)
(e)\(\cos(\pi + t)\)
(f)\(\sin(2\pi - t)\)
- Answer
-
(a) \(\cos(t) = \dfrac{\sqrt{24}}{5}\).
(d) \(\sin(\pi + t) = -\dfrac{1}{5}\).
Exercise \(\PageIndex{35}\)
Suppose that we have the following information about the arc\(t\).
\[\dfrac{\pi}{2} < t < \pi \space and \space \cos(t) = -\dfrac{2}{3}\]
Use this information to determine the exact values of each of the following:
(a)\(\sin(t)\) (b)\(\sin(\pi - t)\) (c)\(\cos(\pi - t)\) (d)\(\sin(\pi + t)\) (e)\(\cos(\pi + t)\) (f)\(\sin(2\pi - t)\)
Exercise \(\PageIndex{36}\)
Make sure your calculator is in Radian Mode.
(a) Use a calculator to find an eight-digit approximation of \(\sin(\dfrac{\pi}{6}+\dfrac{\pi}{4}) = \sin(\dfrac{5\pi}{12})\)
(b) Determine the exact value of \(\sin(\dfrac{\pi}{6}) + \sin(\dfrac{\pi}{4})\).
(c) Use a calculator to find an eight-digit approximation of your result in part (b). Compare this to your result in part (a). Does it seem that
\[\sin(\dfrac{\pi}{6}+\dfrac{\pi}{4}) = \sin(\dfrac{\pi}{6}) + sin(\dfrac{\pi}{4}).\]
(d) Determine the exact value of \(\sin(\dfrac{\pi}{6})\cos(\dfrac{\pi}{4}) + \cos(\dfrac{\pi}{6})\sin(\dfrac{\pi}{4})\).
(e) Determine an eight-digit approximation of your result in part (d).
(f) Compare the results in parts (a) and (e). Does it seem that
\[\sin(\dfrac{\pi}{6}+\dfrac{\pi}{4}) = \sin(\dfrac{\pi}{6})\cos(\dfrac{\pi}{4}) + \cos(\dfrac{\pi}{6})\sin(\dfrac{\pi}{4}).\]
Exercise \(\PageIndex{37}\)
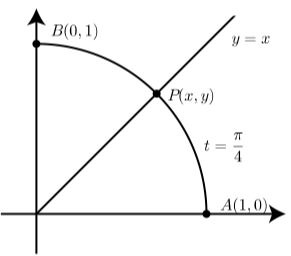
Figure \(\PageIndex{5}\)
This exercise provides an alternate method for determining the exact values of \(\cos(\dfrac{\pi}{4})\) and \(\sin(\dfrac{\pi}{4})\). The diagram shows the terminal point \(P(x, y)\) for an arc of length \(t = \dfrac{\pi}{4}\) on the unit circle. The points \(A(1, 0)\) and \(B(0, 1)\) are also shown.
Since the point B is the terminal point of the arc of length \(\dfrac{\pi}{2}\), we can conclude that the length of the arc from P to B is also \(\dfrac{\pi}{4}\). Because of this, we conclude that the point P lies on the line y D x as shown in the diagram. Use this fact to determine the values of x and y. Explain why this proves that \[\cos(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2} \space and \space \sin(\dfrac{\pi}{4}) = \dfrac{\sqrt{2}}{2}.\]
Exercise \(\PageIndex{38}\)
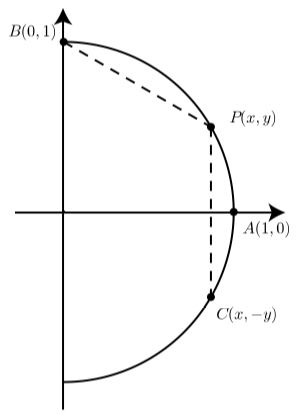
Figure \(\PageIndex{6}\)
This exercise provides an alternate method for determining the exact values of \(\cos(\dfrac{\pi}{6})\) and \(\sin(\dfrac{\pi}{6})\). The diagram shows the terminal point \(P(x, y)\) for an arc of length \(t = \dfrac{\pi}{6}\) on the unit circle. The points \(A(1, 0)\), \(B(0, 1)\), and \(C(x, -y)\) are also shown. Notice that B is the terminal point of the \(arc \space t = -\dfrac{\pi}{6}.\)
We now notice that the length of the arc from P to B is \[\dfrac{\pi}{2} - \dfrac{\pi}{6} = \dfrac{\pi}{3}.\] In addition, the length of the arc from C to P \[\dfrac{\pi}{6} - \dfrac{-\pi}{6} = \dfrac{\pi}{3}.\]
This means that the distance from P to B is equal to the distance from C to P.
(a)Use the distance formula to write a formula (in terms of x and y) for the distance from P to B.
(b)Use the distance formula to write a formula (in terms of x and y) for the distance from C to P .
(c)Set the distances from (a) and (b) equal to each other and solve the resulting equation for y. To do this, begin by squaring both sides of the equation. In order to solve for y, it may be necessary to use the fact that \(x^2 + y^2 = 1\).
(d)Use the value for y in (c) and the fact that x2 C y2 D 1 to determine the value for x. Explain why this proves that \[\cos(\dfrac{\pi}{6}) = \dfrac{\sqrt{3}}{2} \space and \space \sin(\dfrac{\pi}{3}) = \dfrac{1}{2}.\]
Exercise \(\PageIndex{39}\)
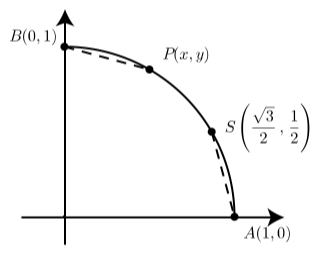
Figure \(\PageIndex{7}\)
This exercise provides an alternate method for determining the exact values of \(\cos(\dfrac{\pi}{3})\) and \(\sin(\dfrac{\pi}{3})\). The diagram shows the terminal point \(P(x, y)\) for an arc of length \(t = \dfrac{\pi}{3}\) on the unit circle. The points \(A(1, 0)\), \(B(0, 1)\), and \(S(\dfrac{\sqrt{3}}{2}, \dfrac{1}{2})\) are also shown. Notice that B is the terminal point of the \(arc \space t = \dfrac{\pi}{2}.\) Notice that B is the terminal point of the \(arc \space t = \dfrac{\pi}{2}.\)
From Exercise (10), we know that \(S\) is the terminal point of an arc of length \(\dfrac{\pi}{6}\).
We now notice that the length of the arc from \(A\) to \(P\) is \(\dfrac{\pi}{3}\). In addition, since the length of the arc from \(A\) to \(B\) is \(\dfrac{\pi}{2}\) and the and the length of the arc from \(B\) to \(P\) is \(\dfrac{\pi}{3}\). This means that the distance from \(P\) to \(B\) is equal \[\dfrac{\pi}{2} - \dfrac{\pi}{3} = \dfrac{\pi}{6}.\] Since both of the arcs have length \(\dfrac{\pi}{6}\), the distance from \(A\) to \(S\) is equal to the distance from \(P\) to \(B\).
(a)Use the distance formula to write a formula (in terms of x and y) for the distance from \(P\) to \(B\).
(b)Use the distance formula to write a formula (in terms of x and y) for the distance from \(P\) to \(B\).
(c)Set the distances from (a) and (b) equal to each other and solve the resulting equation for \(y\). To do this, begin by squaring both sides of the equation. In order to solve for y, it may be necessary to use the fact that \(x^2 + y^2 = 1\).
(d)Use the value for \(y\) in (c) and the fact that \(x^2 + y^2 = 1\)to determine the value for \(x\).
Explain why this proves that \[\cos(\dfrac{\pi}{3}) = \dfrac{1}{2} \space and \space \sin(\dfrac{\pi}{3}) = \dfrac{\sqrt{3}}{2}.\]
Exercise \(\PageIndex{40}\)
Complete the following table with the exact values of each functional value if it is defined.
| \(t\) | \(\cot(t)\) | \(\sec(t)\) | \(\csc(t)\) |
| \(0\) | |||
| \(\dfrac{\pi}{6}\) | |||
| \(\dfrac{\pi}{4}\) | |||
| \(\dfrac{\pi}{4}\) | |||
| \(\dfrac{\pi}{2}\) |
- Answer
-
\(t\) \(\cos(t)\) \(\sec(t)\) \(\csc(t)\) \(0\) undefined \(1\) undefined \(\dfrac{\pi}{6}\) \(\sqrt{3}\) \(\dfrac{2}{\sqrt{3}}\) \(2\) \(\dfrac{\pi}{4}\) \(1\) \(\sqrt{2}\) \(\sqrt{2}\) \(\dfrac{\pi}{3}\) \(\dfrac{1}{\sqrt{3}}\) \(2\) \(\dfrac{2}{\sqrt{3}}\) \(\dfrac{\pi}{2}\) \(0\) undefined \(1\)
Exercise \(\PageIndex{41}\)
Complete the following table with the exact values of each functional value if it is defined.
| \(t\) | \(\cot(t)\) | \(\sec(t)\) | \(\csc(t)\) |
| \(\dfrac{2\pi}{3}\) | |||
| \(\dfrac{7\pi}{6}\) | |||
| \(\dfrac{7\pi}{4}\) | |||
| \(-\dfrac{\pi}{3}\) | |||
| \(\pi\) |
Exercise \(\PageIndex{42}\)
Determine the quadrant in which the terminal point of each arc lies based on the given information.
- \(\cos(x) > 0\) and \(\tan(x) < 0\)
- \(\tan(x) > 0\) and \(\csc(x) < 0\)
- \(\cot(x) > 0\) and \(\sec(x) > 0\)
- \(\sin(x) < 0\) and \(\sec(x) > 0\)
- \(\sec(x) < 0\) and \(\csc(x) > 0\)
- \(\sin(x) < 0\) and \(\cot(x) > 0\)
- Answer
-
(a) The terminal point is in the fourth quadrant.
(b) The terminal point is in the third quadrant.
Exercise \(\PageIndex{43}\)
If \(\sin(t) = \dfrac{1}{3}\) and \(\cos(t) < 0\), determine the exact values of \(\cos(t)\), \(\tan(t)\), \(\csc(t)\), \(\sec(t)\), and \(\cot(t)\).
- Answer
-
- \(\cos(t) = -\dfrac{\sqrt{8}}{3}\)
- \(\tan(t) = -\dfrac{1}{\sqrt{8}}\)
- \(\csc(t) = 3\)
- \(\sec(t) = -\dfrac{3}{\sqrt{8}}\)
- \(\cot(t) = -\sqrt{8}\)
Exercise \(\PageIndex{44}\)
If \(\cos(t) = -\dfrac{3}{5}\) and \(\sin(t) < 0\), determine the exact values of \(\sin(t)\), \(\tan(t)\), \(\csc(t)\), \(\sec(t)\), and \(\cot(t)\).
Exercise \(\PageIndex{45}\)
If \(\sin(t) = -\dfrac{2}{5}\) and \(\tan(t) < 0\), determine the exact values of \(\cos(t)\), \(\tan(t)\), \(\csc(t)\), \(\sec(t)\), and \(\cot(t)\).
Exercise \(\PageIndex{46}\)
If \(\sin(t) = 0. 273\) and \(\cos(t) < 0\), determine the five-digit approximations for \(\cos(t)\), \(\tan(t)\), \(\csc(t)\), \(\sec(t)\), and \(\cot(t)\).
Exercise \(\PageIndex{47}\)
In each case, determine the arc t that satisfies the given conditions or explain why no such arc exists.
- \(\tan(t) = 1, \cos(t) = -\dfrac{1}{\sqrt{2}}, and 0< t < 2\pi\)
- \(\sin(t) = 1, \sec(t)\) is undefined, and \(0< t < \pi\)
- \(\sin(t) = \dfrac{\sqrt{2}}{2}, \sec(t) = -\sqrt{2}, and 0< t < \pi\)
- \(\sec(t) = -\dfrac{2}{\sqrt{3}}, \tan(t) = \sqrt{2}, and 0< t < 2\pi\)
- \(\csc(t) = \sqrt{2}, \tan(t) = -1, and 0< t < 2\pi\)
- Answer
-
(a) \(t = \dfrac{5\pi}{4}\)
(b) \(t = \dfrac{\pi}{2}\)
Exercise \(\PageIndex{48}\)
Use a calculator to determine four-digit decimal approximations for each of the following.
- \(\csc(1)\)
- \(\tan(\dfrac{12\pi}{5})\)
- \(\cot(t)\)
- \(\sec(\dfrac{13\pi}{8})\)
- \(\sin^2(5.5)\)
- \(1 + \tan^2(2)\)
- \(\sec^2(2)\)

