2.1: Graphs of the Cosine and Sine Functions
- Page ID
- 7104
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Focus Questions
The following questions are meant to guide our study of the material in this section. After studying this section, we should understand the concepts motivated by these questions and be able to write precise, coherent answers to these questions.
- What are the graphs and important properties of the graphs of \(y = \cos(x)\) and \(y = \sin(x)\)?
- What are the domains of the sine and cosine functions? What are the ranges of the sine and cosine functions?
- What are the periods of the sine and cosine functions? What does period mean?
- What is amplitude? How does the amplitude affect the graph of the sine or cosine?
Beginning Activity
The most basic form of drawing the graph of a function is to plot points. Use the values in the given table to plot the points on the graph of \(y = \sin(x)\) and then draw the graph of \(y = \sin(t)\) for \(0 < t < 2\pi\). Note: On the \(t\)-axis, the gridlines are \(\dfrac{\pi}{12}\) units apart and on the \(y\)-axis, the gridlines are 0.1 of a unit apart.

| \(t\) | \(\sin(t)\) | \(\sin(t)\) (approx) |
|---|---|---|
| 0 | 0 | 0 |
| \(\dfrac{\pi}{6}\) | \(\dfrac{1}{2}\) | 0.5 |
| \(\dfrac{\pi}{4}\) | \(\dfrac{\sqrt{2}}{2}\) | 0.707 |
| \(\dfrac{\pi}{3}\) | \(\dfrac{\sqrt{3}}{2}\) | 0.866 |
| \(\dfrac{\pi}{2}\) | 1 | 1 |
| \(\dfrac{2\pi}{3}\) | \(\dfrac{\sqrt{3}}{2}\) | 0.866 |
| \(\dfrac{3\pi}{4}\) | \(\dfrac{\sqrt{2}}{2}\) | 0.714 |
| \(\dfrac{5\pi}{6}\) | \(\dfrac{1}{2}\) | 0.5 |
| \(\pi\) | 0 | 0 |
| \(\dfrac{7\pi}{6}\) | \(-\dfrac{1}{2}\) | -0.5 |
| \(\dfrac{5\pi}{4}\) | \(-\dfrac{\sqrt{2}}{2}\) | -0.707 |
| \(\dfrac{4\pi}{3}\) | \(-\dfrac{\sqrt{3}}{2}\) | -0.866 |
| \(\dfrac{3\pi}{2}\) | -1 | -1 |
| \(\dfrac{5\pi}{3}\) | \(-\dfrac{\sqrt{3}}{2}\) | -0.866 |
| \(\dfrac{7\pi}{4}\) | \(-\dfrac{\sqrt{2}}{2}\) | -0.707 |
| \(\dfrac{11\pi}{6}\) | \(-\dfrac{1}{2}\) | -0.5 |
| \(2\pi\) | 0 | 0 |
We can also use a graphing calculator or other graphing device to draw the graph of the sine function. Make sure the device is set to radian mode and use it to draw the graph of \(y = \sin(t)\) using \(-2\pi \leq t \leq 4\pi\) and \(-1.2 \leq t \leq 1.2\). Note: Many graphing utilities require the use of \(x\) as the independent variable. For such devices, we need to use \(y = \sin(x)\). This will make no difference in the graph of the function.
- Compare this to the graph from part (1). What are the similarities? What are the differences?
- Find four separate values of \(t\) where the graph of the sine function crosses the \(t\)-axis. Such values are called \(t\)-intercepts of the sine function (or roots or zeros).
- Based on the graphs, what appears to be the maximum value of \(\sin(t)\). Determine two different values of \(t\) that give this maximum value of \(\sin(t)\).
- Based on the graphs, what appears to be the minimum value of \(\sin(t)\). Determine two different values of \(t\) that give this minimum value of \(\sin(t)\).
The Periods of the Sine and Cosine Functions
One thing we can observe from the graphs of the sine function in the beginning activity is that the graph seems to have a “wave” form and that this “wave” repeats as we move along the horizontal axis. We see that the portion of the graph between 0 and \(2\pi\) seems identical to the portion of the graph between \(2\pi\) and \(4\pi\) and to the portion of the graph between \(-2\pi\) and 0. The graph of the sine function is exhibiting what is known as a periodic property. Figure 2.1 shows the graph of \(y = \sin(t)\) for three cycles.
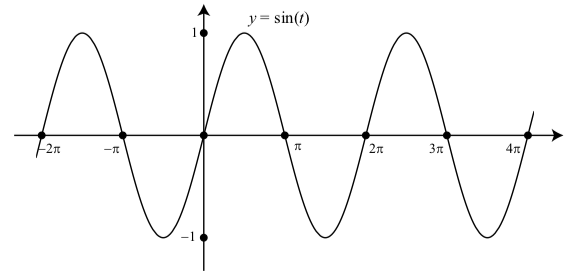
Figure \(\PageIndex{1}\): Graph of \(y = \sin(t)\) with \(-2\pi \leq t \leq 4\pi\)
We say that the sine function is a periodic function. Such functions are often used to model repetitious phenomena such as a pendulum swinging back and forth, a weight attached to a spring, and a vibrating guitar string.
The reason that the graph of \(y = \sin(t)\) repeats is that the value of \(\sin(t)\) is the y-coordinate of a point as it moves around the unit circle. Since the circumference of the unit circle is \(2\pi\) units, an arc of length \((t + 2\pi)\) will have the same terminal point as an arc of length t. Since \(\sin(t)\) is the y-coordinate of this point, we see that \(\sin(t + 2\pi) = \sin(t)\). This means that the period of the sine function is \(2\pi\). Following is a more formal definition of a periodic function.
Definition
Definition. A function \(f\) is periodic with period \(p\) if \(f(t + p) = f(t)\) for all \(t\) in the domain of \(f\) and \(p\) is the smallest positive number that has this property.
Notice that if \(f\) is a periodic function with period \(p\), then if we add 2\(p\) to \(t\), we get \[f(t + 2p) = f((t+p)+p) = f(t + p) =f(t).\]
We can continue to repeat this process and see that for any integer \(k\), \[f(t + kp) =f(t).\]
So far, we have been discussing only the sine function, but we get similar behavior with the cosine function. Recall that the wrapping function wraps the number line around the unit circle in a way that repeats in segments of length \(2\pi\). This is periodic behavior and it leads to periodic behavior of both the sine and cosine functions since the value of the sine function is the \(y\)-coordinate of a point on the unit circle and the value of the cosine function is the \(x\)-coordinate of the same point on the unit circle, the sine and cosine functions repeat every time we make one wrap around the unit circle. That is, \[\cos(t + 2\pi) = \cos(t) \space and \space \sin(t + 2\pi) = \sin(t).\]
It is important to recognize that \(2\pi\) is the smallest number that makes this happen. Therefore, the cosine and sine functions are periodic with period \(2\pi\).
Exercise \(\PageIndex{1}\)
We can, of course, use a graphing utility to draw the graph of the cosine function. However, it does help to understand the graph if we actually draw the graph by hand as we did for the sine function in the beginning activity. Use the values in the given table to plot the points on the graph of \(y = \cos(t)\) and then draw the graph of \(y = \cos(t)\) for \(0 \leq t \leq 2\pi\).

| \(t\) | \(\cos(t)\) | \(\cos(t)\) (approx) |
|---|---|---|
| \(0\) | \(1\) | \(1\) |
| \(\dfrac{\pi}{6}\) | \(\dfrac{\sqrt{3}}{2}\) | \(0.866\) |
| \(\dfrac{\pi}{4}\) | \(\dfrac{\sqrt{2}}{2}\) | \(0.707\) |
| \(\dfrac{\pi}{3}\) | \(\dfrac{1}{2}\) | \(0.5\) |
| \(\dfrac{\pi}{2}\) | \(0\) | \(0\) |
| \(\dfrac{2\pi}{3}\) | \(-\dfrac{1}{2}\) | \(-0.5\) |
| \(\dfrac{3\pi}{4}\) | \(-\dfrac{\sqrt{2}}{2}\) | \(-0.714\) |
| \(\dfrac{5\pi}{6}\) | \(-\dfrac{\sqrt{3}}{2}\) | \(-0.866\) |
| \(\pi\) | \(-1\) | \(-1\) |
| \(\dfrac{7\pi}{6}\) | \(-\dfrac{\sqrt{3}}{2}\) | \(-0.866\) |
| \(\dfrac{5\pi}{4}\) | \(-\dfrac{\sqrt{2}}{2}\) | \(-0.714\) |
| \(\dfrac{4\pi}{3}\) | \(-\dfrac{1}{2}\) | \(-0.5\) |
| \(\dfrac{3\pi}{2}\) | \(0\) | \(-1\) |
| \(\dfrac{5\pi}{3}\) | \(\dfrac{1}{2}\) | \(0.5\) |
| \(\dfrac{7\pi}{4}\) | \(-\dfrac{\sqrt{2}}{2}\) | \(0.707\) |
| \(\dfrac{11\pi}{6}\) | \(\dfrac{\sqrt{3}}{2}\) | \(-0.866\) |
| \(2\pi\) | \(1\) | \(1\) |
- Answer
-
Not all of the points are plotted, but the following is a graph of one complete period of \(y = \cos(t)\) for \(0 \leq t \leq 2\pi\).
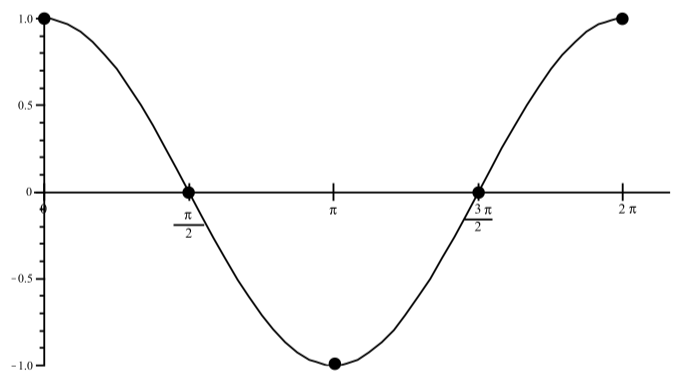

Figure \(\PageIndex{2}\): Graph of \(y = \cos(t)\) with \(-2\pi \leq t \leq 4\pi\)
Exercise \(\PageIndex{2}\)
- Compare the graph in Figure \(\PageIndex{2}\) to the graph from Exercise \(\PageIndex{1}\). What are the similarities? What are the differences?
- Find four separate values of \(t\) where the graph of the cosine function crosses the \(t\)-axis. Such values are called \(t\)-intercepts of the cosine function (or roots or zeros).
- Based on the graphs, what appears to be the maximum value of \(\cos(t)\). Determine two different values of \(t\) that give this maximum value of \(\cos(t)\).
- Based on the graphs, what appears to be the minimum value of \(\cos(t)\). Determine two different values of \(t\) that give this minimum value of \(\cos(t)\).
- Answer
-
- The difference is that the graph in Figure \(\PageIndex{2}\) shows three complete periods of \(y = \cos(t)\) over the interval \([-2\pi, 4\pi]\).
- The graph of \(y = \cos(t)\) has \(t\)-intercepts at \(t = -\dfrac{3\pi}{2}, t = -\dfrac{\pi}{2}, t = \dfrac{\pi}{2}, t = \dfrac{3\pi}{2}, t = \dfrac{5\pi}{2}\), and \(t = \dfrac{7\pi}{2}\)
- The maximum value of \(y = \cos(t)\) is \(1\). The graph attains this maximum at \(t = -2\pi, t = 0, t = 2\pi\), and \(t = 4\pi\).
- The minimum value of \(y = \cos(t)\) is \(-1\). The graph attains this minimum at \(t = -\pi, t = \pi\), and \(t = 3\pi\)
Activity 2.3 (The Graphs of the Sine and Cosine Functions).
We have now constructed the graph of the sine and cosine functions by plotting points and by using a graphing utility. We can have a better understanding of these graphs if we can see how these graphs are related to the unit circle definitions of \(\sin(t)\) and \(\cos(t)\). We will use two Geogebra applets to help us do this.
The first applet is called Sine Graph Generator. The web address is gvsu.edu/s/Ly
To begin, just move the slider for \(t\) until you get \(t = 1\) and observe the resulting image. On the left, there will be a copy of the unit circle with an arc drawn that has length \(1\). The \(y\)-coordinate of the terminal point of this arc (\(0.84\) rounded to the nearest hundredth) will also be displayed. The horizontal line will be connected to the point \((1, 0.84)\) on the graph of \(y = \sin(t)\). As the values of \(t\) are changed with the slider, more points will be drawn in this manner on the graph of \(y = \sin(t)\).
The other applet is called Cosine Graph Generator and it works in a manner similar to Sine Graph Generator. The web address for this applet is http://gvsu.edu/s/Lz
Properties of the Graphs of the Sine and Cosine Functions
The graphs of \(y = \sin(t)\) and \(y = \cos(t)\) are called sinusoidal waves and the sine and cosine functions are called sinusoidal functions. Both of these particular sinusoidal waves have a period of \(2\pi\). The graph over one period is called a cycle of the graph. As with other functions in our previous study of algebra, another important property of graphs is their intercepts, in particular, the horizontal intercepts or the points where the graph crosses the horizontal axis. One big difference from algebra is that the sine and cosine functions have infinitely many horizontal intercepts.
In Exercise \(\PageIndex{2}\), we used Figure \(\PageIndex{2}\) and determined that \(-\dfrac{\pi}{2}, \dfrac{\pi}{2}, \dfrac{3\pi}{2}, \dfrac{5\pi}{2}, \dfrac{7\pi}{2}\) are \(t\)-intercepts on the graph of \(y = \cos(t)\). In particular, in the interval \([0, 2\pi]\), the only \(t\)-intercepts of \(y = \cos(t)\) are \(t = \dfrac{\pi}{2}\) and \(t = \dfrac{3\pi}{2}\).
There are, of course, other \(t\)-intercepts, and this is where the period of \(2\pi\) is helpful. We can generate any other \(t\)-intercept of \(y = \cos(t)\) by adding integer multiples of the period \(2\pi\) to these two values. For example, if we add \(6\pi\) to each of them, we see that \(t = \dfrac{13\pi}{2}\) and \(t = \dfrac{15\pi}{2}\) are \(t\) intercepts of \(y = \cos(t)\).
Exercise \(\PageIndex{3}\)
Use a graph to determine the \(t\)-intercepts of \(y = \sin(t)\) in the interval \([0, 2\pi]\). Then use the period property of the sine function to determine the \(t\)-intercepts of \(y = \sin(t)\) in the interval \([-2\pi, 4\pi]\). Compare this result to the graph in Figure 2.1. Finally, determine two \(t\)-intercepts of \(y = \sin(t)\) that are not in the interval \([-2\pi, 4\pi]\).
- Answer
-
The graph of \(y = \sin(t)\) has \(t\)-intercepts of \(t = 0, t = \pi\), and \(t = 2\pi\) in the interval \([0, 2\pi]\).
If we add the period of \(2\pi\) to each of these \(t\)-intercepts and subtract the period of \(2\pi\) from each of these \(t\)-intercepts, we see that the graph of \(y = \sin(t)\) has \(t\)-intercepts of \(t = -2\pi, t = -\pi, t = 0, t = \pi, t = 2\pi, t = 3\pi\), and \(t = 4\pi\) in the interval \([-2\pi, 4\pi]\).We can determine other \(t\)-intercepts of \(y = \sin(t)\) by repeatedly adding or subtracting the period of \(2\pi\). For example, there is a \(t\)-intercept at:
- \(t = 3\pi + 2\pi = 5\pi\)
- \(t = 5\pi + 2\pi = 7\pi\)
However, if we look more carefully at the graph of \(y = \sin(t)\), we see that the \(t\)-intercepts are spaced \(\pi\) units apart. This means that we can say that \(t = 0 + k\pi\), where \(k\) is some integer, is a \(t\)-intercept of \(y = \sin(t)\).
Activity 2.5 (Exploring Graphs of Sine Functions)
Do one of the following:
- Draw the graphs of \(y = \sin(t)\), \(y = \dfrac{1}{2}\sin(t)\) and \(y = 2\sin(t)\), \(y = -\sin(t)\), and \(y = 2\sin(t)\) on the same axes. Make sure your graphing utility is in radian mode and use \(-2\pi \leq x \leq 2\pi\) and \(-2.5 \leq x \leq 2.5\).
- Use the Geogebra applet Amplitude of a Sinusoid at the following web address: http://gvsu.edu/s/LM
The expression for \(g(t)\) can be changed but leave it set to \(g(t) = \sin(t)\). The slider can be moved to change the value of A and the graph of \(y = A\sin(t)\) will be drawn. Explore these graphs by changing the values of A making sure to use negative values of A as well as positive values of A. (It is possible to change this to \(g(t) = \cos(t)\) and explore the graphs of \(y = A\sin(t)\).
The Amplitude of Sine and Cosine Functions
The graphs of the functions from Activity 2.5 should have looked like one of the graphs in Figure 2.3. Both graphs are graphs of \(y = A\sin(t)\), but the one on the left is for \(A > 0\) and the one on the right is for \(A < 0\). Note that when \(A < 0\), \(-A > 0\). Another important characteristic of a sinusoidal wave is the amplitude. The amplitude of each of the graphs in Figure 2.3 is represented by the length of the dashed lines, and we see that this length is equal to \(|A|\).
Definition: amplitude
The amplitude of a sinusoidal wave is one-half the distance between the maximum and minimum functional values.
\[\text{Amplitude} = \dfrac{1}{2}|(\text{ max y-coordinate}) - (\text{min y-coordinate})|\]
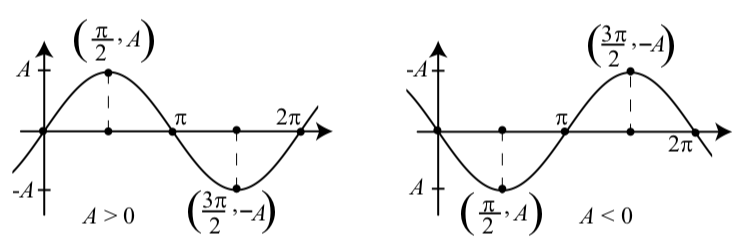
Figure \(\PageIndex{3}\): Graphs of \(y = A\sin(t)\)
Exercise \(\PageIndex{4}\)
Draw graphs of \(y = A\cos(t)\) for \(A > 0\) and for \(A < 0\) similar to the graphs for \(y = A\sin(t)\) in Figure \(\PageIndex{3}\).
- Answer
-
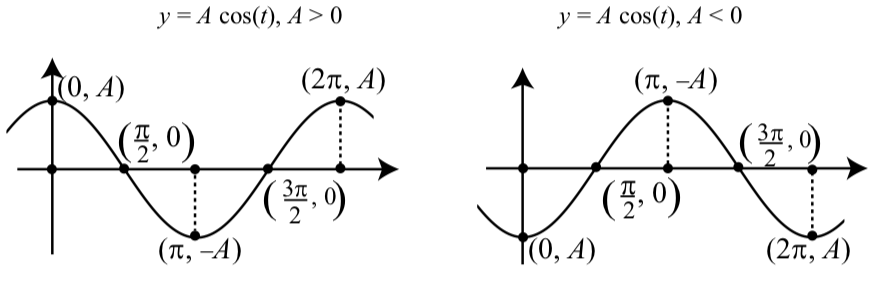
Using a Graphing Utility
We often will use a graphing utility to draw the graph of a sinusoidal function. When doing so, it is a good idea to use the amplitude to help set an appropriate viewing window. The basic idea is to have the screen on the graphing utility show slightly more than one period of the sinusoid. For example, if we are trying to draw a graph of \(y = 3.6\cos(t)\), we could use the following viewing window. \[-0.5 \leq x \leq 6.5 \space and \space -4 \leq y \leq 4.\] If it is possible, set the \(x\)-tickmarks to be every \(\dfrac{\pi}{4}\) or \(\dfrac{\pi}{2}\) units.
Exercise \(\PageIndex{5}\)
- Use a graphing utility to draw the graph of \(y = 3.6\cos(t)\) using the viewing window stated prior to this progress test.
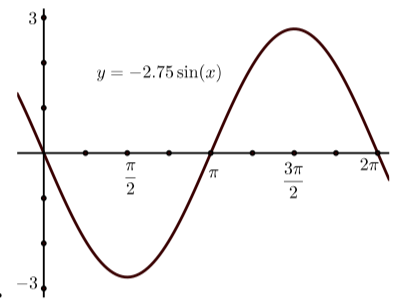
- Use a graphing utility to draw the graph of \(y = -2.75\sin(t)\).
- Answer
-
1.
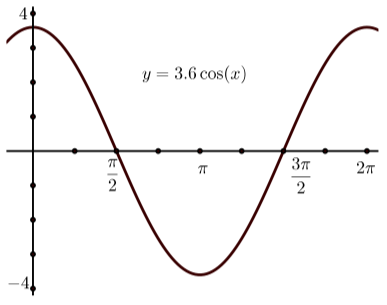
2.
Symmetry and the Negative Identities
Examine the graph of \(y = \cos(t)\) shown in Figure 2.2. If we focus on that portion of the graph between \(-2\pi\) and \(2\pi\), we can notice that the left side of the graph is the “mirror image” of the right side of the graph. To see this better, use the Geogebra applet Symmetry of the Graph of \(y = \cos(t)\) at the following link: http://gvsu.edu/s/Ot
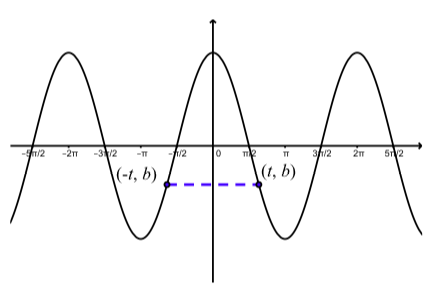
Figure \(\PageIndex{4}\): Graph Showing Symmetry of \(y = \cos(t)\)
Figure \(\PageIndex{4}\) shows a typical image from this applet. Since the second coordinate of a point on the graph is the value of the function at the first coordinate, this figure (and applet) are indicating that \(b = \cos(t)\) and \(b = \cos(-t)\). That is, this is illustrating the fact that \(\cos(-t) = \cos(t)\). The next activity provides an explanation as to why this is true.
Activity 2.8: Positive and Negative Arcs
For this activity, we will use the Geogebra applet called Drawing a Positive Arc and a Negative Arc on the Unit Circle. A link to this applet is http://gvsu.edu/s/Ol
As the slider for \(t\) in the applet is used, an arc of length t will be drawn in blue and an arc of length \(-t\) will be drawn in red. In addition, the coordinates of the terminal points of both the arcs \(t\) and \(-t\) will be displayed. Study the coordinates of these two points for various values of \(t\). What do you observe? Keeping in mind that the coordinates of these points can also be represented as \[(\cos(t), \sin(t))\space and \space (\cos(-t), \sin(-t)),\]
what does these seem to indicate about the relationship between \(\cos(-t)\) and \(\cos(t)\)? What about the relationship between \(\sin(-t)\) and \(\sin(t)\)?
Figure \(\PageIndex{5}\) shows a typical situation illustrated in Activity 2.8. An arc and it corresponding negative arc have been drawn on the unit circle. What we have seen
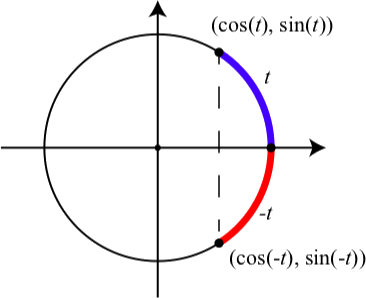
Figure \(\PageIndex{5}\): An Arc and a Negative Arc on the Unit Circle
is that if the terminal point of the arc \(t\) is \((a, b)\), then by the symmetry of the circle, we see that the terminal point of the arc \(-t\) is \((a, -b)\). So the diagram illustrates the following results, which are sometimes called negative arc identities.
Definition: Negative Arc Identities
For every real number \(t\), \[\sin(-t) = -\sin(t) \space \cos(-t) = \cos(t).\]
To further verify the negative arc identities for sine and cosine, use a graphing utility to:
- Draw the graph of \(y = \cos(-x)\) using \(0 \leq x \leq 2\pi\). The graph should be identical to the graph of \(y = \cos(x)\).
- Draw the graph of \(y = \sin(-x)\) using \(0 \leq x \leq 2\pi\). The graph should be identical to the graph of \(y = \sin(x)\).
These so-called negative arc identities give us a way to look at the symmetry of the graphs of the cosine and sine functions. We have already illustrated the symmetry of the cosine function in Figure \(\PageIndex{4}\). Because of this, we say the graph of \(y = \cos(t)\) is symmetric about the y-axis.
What about symmetry in the graph of the sine function? Figure \(\PageIndex{6}\) illustrates what the negative identity \(\sin(-t) = \sin(t)\) implies about the symmetry of \(y = \sin(t)\). In this case, we say the graph of \(y = \sin(t)\) is symmetric about the origin.
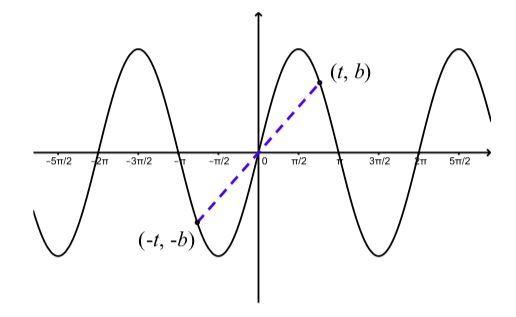
Figure \(\PageIndex{6}\): Graph Showing Symmetry of \(y = \sin(t)\).
To see the symmetry of the graph of the sine function better, use the Geogebra applet Symmetry of the Graph of \(y = \sin(t)\) at the following link: http://gvsu.edu/s/Ou
Summary
In this section, we studied the following important concepts and ideas:
- The important characteristics of sinusoidal functions of the form \(y = A\sin(t)\) or \(y = A\cos(t)\) shown in Table 2.1.
- The information in Table 2.1 can seem like a lot to remember, and in fact, in the next sections, we will get a lot more information about sinusoidal waves. So instead of trying to remember everything in Table 2.1, it is better to remember the basic shapes of the graphs as shown in Figure \(\PageIndex{7}\) and Figure \(\PageIndex{8}\).
| \(y = A\sin(t)\) | \(y = A\cos(t)\) | |
|---|---|---|
| All real numbers | domain | All real numbers |
| \(2\pi\) | period | \(2\pi\) |
| \(|A|\) | amplitude | \(|A|\) |
| \((0, 0)\) | \(y\)-intercept | \((0, A)\) |
| \(t = 0\) and \(t = \pi\) | \(t\)-intercept in \([0, 2\pi)\) | \(t = \dfrac{\pi}{2}\) and \(t = \dfrac{3\pi}{2}\) |
| \(|A|\) | maximum value | \(|A|\) |
| \(-|A|\) | minimum value | \(-|A|\) |
| The interval \([-|A|, |A|]\) | range | The interval \([-|A|, |A|]\) |
| \(t = \dfrac{\pi}{2}\) | when \(A > 0\), maximum occurs at | \(t = 0\) |
| \(t = \dfrac{3\pi}{2}\) | when \(A > 0\), maximum occurs at | \(t = \pi\) |
| \(t = \dfrac{3\pi}{2}\) | when \(A < 0\), maximum occurs at | \(t = \pi\) |
| \(t = \dfrac{\pi}{2}\) | when \(A < 0\), maximum occurs at | \(t = 0\) |
| the origin | symmetry with respect to | the \(y\)-axis |
- One way to remember the location of the tick-marks on the \(t\)-axis is to remember the spacing for these tick-marks is one-quarter of a period and the period is \(2\pi\). So the spacing \(\dfrac{2\pi}{4} = \dfrac{\pi}{2}\).
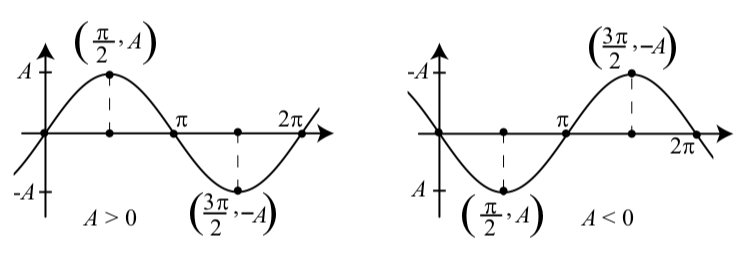
Figure \(\PageIndex{7}\): Graphs of \(y = A\sin(t)\).
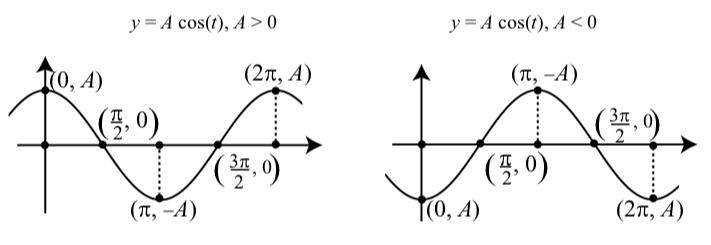
Figure \(\PageIndex{8}\): Graphs of \(y = A\cos(t)\).
Supplemental Material – Even and Odd Functions
There is a more general mathematical context for these types of symmetry, and that has to do with what are called even functions and odd functions.
Definitions: even and Odd functions
- A function \(f\) is an even function if \(f(-x) = f(x)\) for all \(x\) in the domain of \(f\).
- A function \(f\) is an odd function if \(f(-x) = -f(x)\) for all \(x\) in the domain of \(f\).
So with these definitions, we can say that the cosine function is an even function and the sine function is an odd function. Why do we use these terms? One explanation is that the concepts of even functions and odd functions are used to describe functions \(f\) of the form \(f(x) = x^n\) for some positive integer \(n\), and the graphs of these functions exhibit different types of symmetry when \(n\) is even versus when \(n\) is odd.
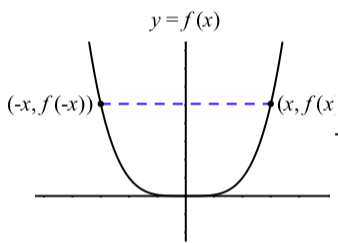
Figure \(\PageIndex{9}\): \(f(x) = x^n\), n even and \(f(-x) = f(x)\)
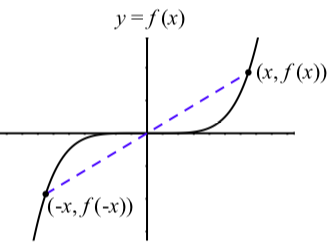
Figure \(\PageIndex{10}\): \(f(x) = x^n\), \(n\) odd and \(f(-x) = -f(x)\).
In Figure \(\PageIndex{9}\), we see that when \(n\) is even, \(f(-x) = f(x)\) since \((-x)^n = x^n\). So the graph is symmetric about the \(y\)-axis. When \(n\) is odd as in Figure \(\PageIndex{10}\), \(f(-x) = -f(x)\) since \((-x)^n = -x^n\). So the graph is symmetric about the origin. This is why we use the term even functions for those functions \(f\) for which \(f(-x) = f(x)\), and we use the term odd functions for those functions for which \(f(-x) = -f(x)\).


