8.4: Quadratic Sequences

Last updated
Save as PDF

Page ID: 83161

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Quadratic functions are polynomial functions of degree two. For example, $f(x) = x^2$ is a quadratic function. This section will explore patterns in quadratic functions and sequences. Identifying patterns within a function table gives us valuable clues to build the right function to match the mathematical pattern.

How to Detect a Quadratic Sequence:

Unlike an arithmetic sequence which has a common difference $d = a_n − a_{n-1}$, the quadratic sequence will not have a common difference until the second difference is taken, or the difference of the difference!

Consider the sequence: $1, 4, 9, 16, 25, …$ which has general term $a_n = n^2$.

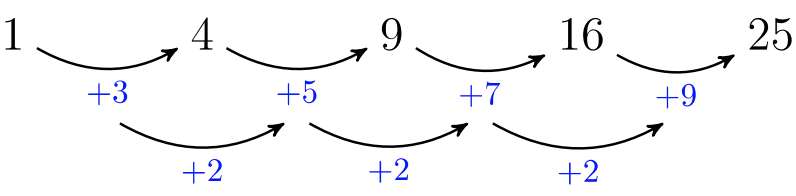
$clipboard_e10f4db8ad881b673244db0e5caf99a44.png$

The first difference was taken, but we did not find a common difference. The first difference gives the uncommon values: $3, 5, 7, 9$. However, we persisted and took a difference of the differences: $5 − 3 = 2$, $7 − 5 = 2$, and $9 − 7 = 2$. The second layer of differences revealed a common value: $2$. The sequence is a quadratic sequence if the first difference does not have a common difference, but the second difference does!

The sequence of squares is another beautiful visual. What’s more, the visual truly justifies why we call these numbers “squares.”

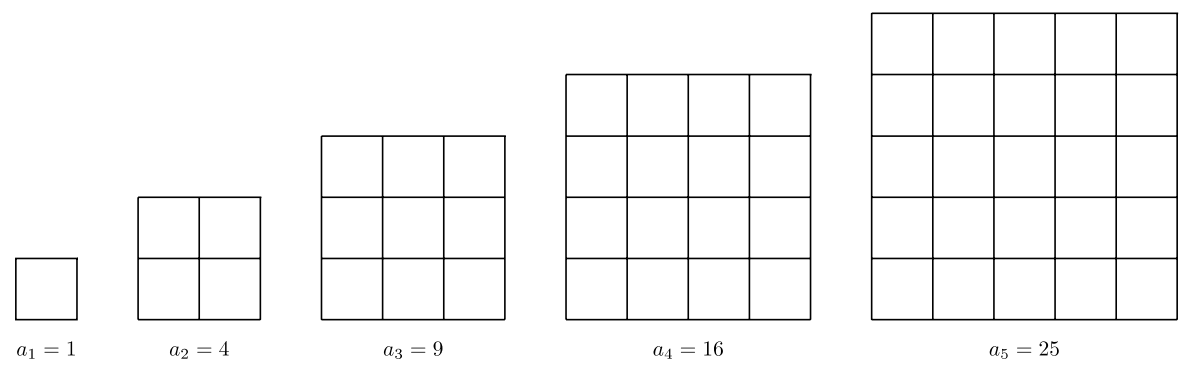
$clipboard_e93697812888fa20e1802dca89e35476a.png$

It is also remarkable that the sequence of squares can be created by the sequence of partial sums of odd numbers. The wonder of mathematics continues to astound us!

$\begin{array} &a_1 &= 1 \\ a_2 &= 1 + 3 = 4 \\ a_3 &= 1 + 3 + 5 = 9\\ a_4 &= 1 + 3 + 5 + 7 = 16\\ a_5 &= 1 + 3 + 5 + 7 + 9 = 25 \\ \text{etc.} \end{array}$

Example 8.4.1

Consider the pattern below. How many small square tiles will be in the $10^{\text{th}}$ stage $(a_{10})$ of this pattern?

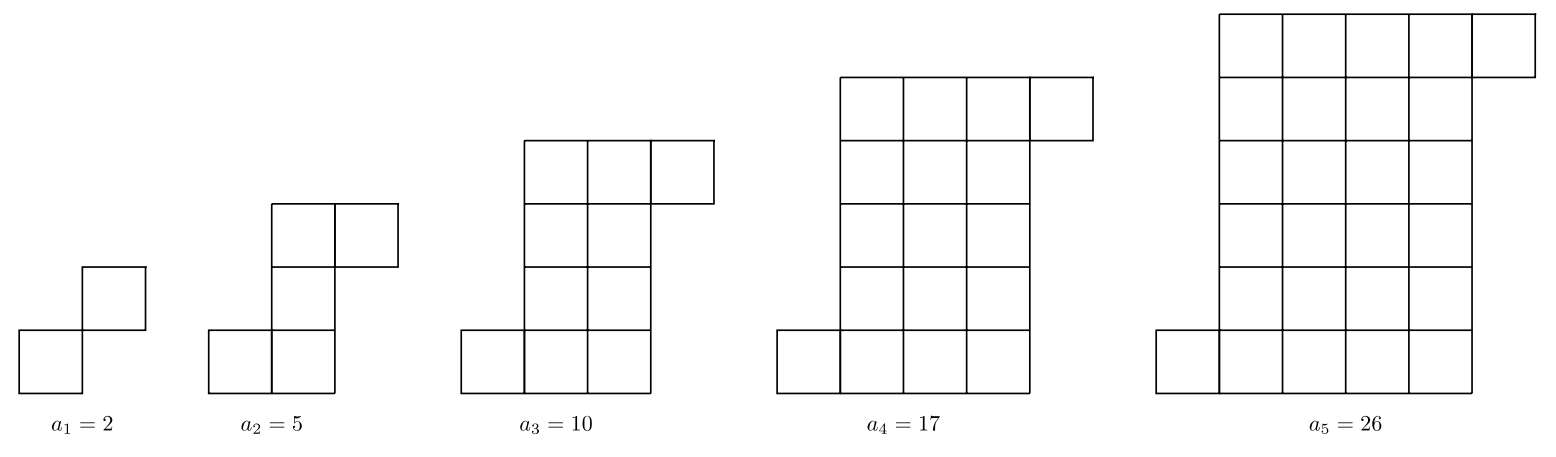
$clipboard_e21a3abd6fe152df245e014a981984c16.png$

Solution

The pattern is a quadratic sequence:

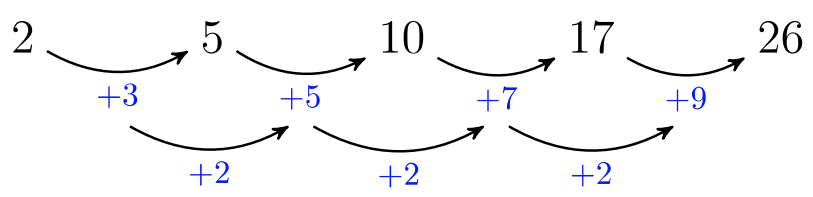
$clipboard_e05ac4753677f723394a7473851517c81.png$

We can view $2$ separate patterns. The $2^{\text{nd}}$, $3^{\text{rd}}$, $4^{\text{th}}$, and $5^{\text{th}}$ figures contain a pattern of squares: $1, 4, 9, 16, …$ Below, the squares are shaded yellow that create the Pattern of squares. The top and bottom rows create a linear pattern (blue), which is an arithmetic sequence.

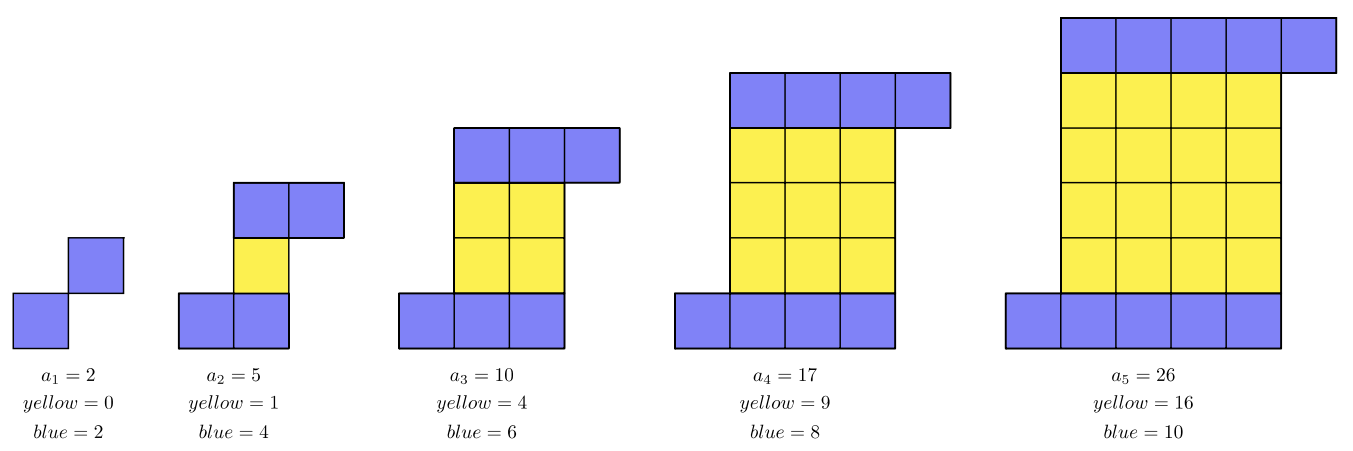
$clipboard_e9d0bbc2917ae3643c5be323ec9e848e0.png$

The blue sequence is $2, 4, 6, 8, 10, …$ which has general term $b_n = 2n$

The yellow sequence is $0, 1, 4, 9, 16, …$ which has general term $y_n = (n − 1)^2$

The blue and the yellow sequence together make the overall figure’s sequence, $a_n$.

$\begin{array} &a_n &= b_n + y_n &\text{blue sequence \(+$ yellow sequence $= a_n$} \\ a_n &= 2n + (n − 1)^2 &\text{Substitute the sequence general term.} \\ a_n &= \underbrace{2n}_{\text{blue}} + \underbrace{n^2-2n+1}_{\text{yellow}} &\text{Expand, using FOIL.} \\ a_n &= n^2 + 1 &\text{Simplify.} \end{array}\)

Example 8.4.2

The first $4$ stages of a pattern are shown below. How many circles will be required to construct the $25^{\text{th}}$ stage $(a_{25})$?

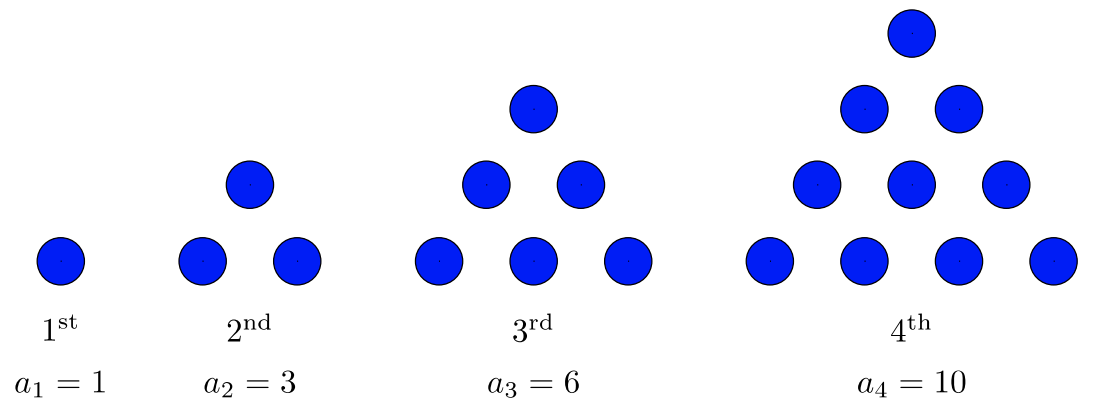
$clipboard_e4ae54cfeeffa20ee9084fa66a7da6bfd.png$

Solution

The number of circles in each figure creates a quadratic sequence, which we can see by finding the common difference in the second difference.

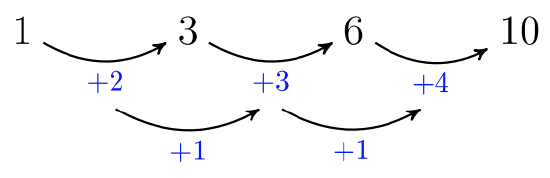
$clipboard_e6213b7767195bb57dc16e6fc190ac83c.png$

The challenge here is to find the value $(a_{25})$. Although there are many approaches one could take, this is one method to find $(a_{25})$.

Notice that the sequence $1, 3, 6, 10, …$ is the sequence of partial sums of consecutive numbers:

Therefore, $a_{25} = 1 + 2 + 3 + ⋯ + 25$. Rather than performing the addition one term at a time, let’s write the sum twice: one increasing, and one decreasing, then add vertically. A cool thing happens:

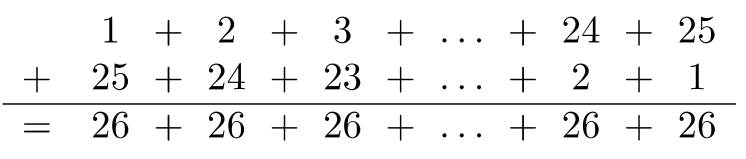
$clipboard_e9460b09125c0deee5cfcca9a452ac288.png$

Therefore,

$\begin{array} &a_{25} + a_{25} &= 25 \cdot 26 \\ 2a_{25} &= 650 \\ \dfrac{2a_{25}}{2} &= \dfrac{650}{2} \\ a_{25} &= 325 \end{array}$

Adding Consecutive Numbers: 1 to n:

The previous example (Example 8.4.2) demonstrated a method for finding the sum of the first $25$ consecutive numbers.

$1 + 2 + 3 + ⋯ + 25 = \dfrac{25 \cdot 26}{2}$

Let’s generalize finding $s_n$, the sum of the first $n$ consecutive natural numbers. Again, using the method of Example $8.4.2$:

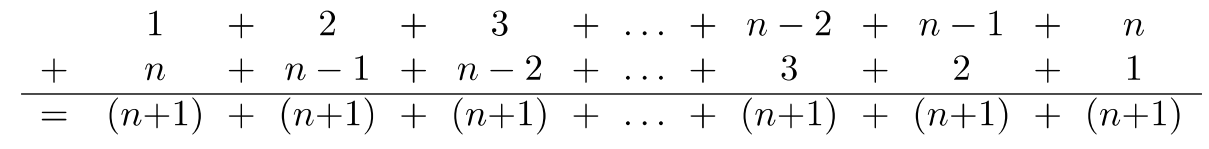
$clipboard_e7018fea7e73a8a8cead911c1d1616c3b.png$

Therefore,

$\begin{array} & s_n + s_n &= n(n + 1) \\ 2s_n &= n(n + 1) \\ \dfrac{2s_n}{2} &= \dfrac{n(n + 1)}{2} \\ s_n &= \dfrac{n(n + 1)}{2} \end{array}$

Example 8.4.3

On his first day of class, Jackson’s teacher asks that student shake hands and introduce themselves to each other. There are $25$ students in the class. How many different handshakes can occur during this icebreaker if every student shakes hands with every other student?

Solution

An important step to problem solving is to understand the problem. Let’s start small. Suppose there are only $2$ people in a class. If Chloe shakes hands with Jackson, one handshake has occurred, and that’s it! Now let’s add another person to the room and consider a class of $3$ students. Then add another for a class size of $4$. Then another…and create a chart of results.

$n =$ class size	$b_n =$ handshakes
$2$	$1$
$3$	$3$
$4$	$6$
$5$	$10$

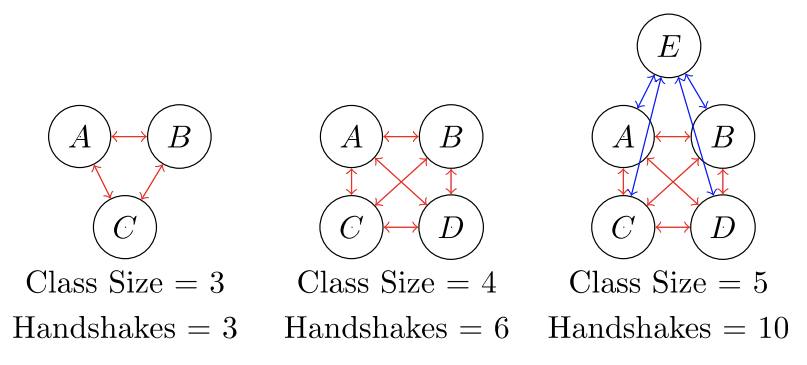
$clipboard_e4564a6e2c5f0912035055e15b5bab059.png$

A pattern emerges much like the previous example (Example 8.4.2). However, the $n$-values (class size) are one more than the $n$-values (the figure number) in Example 8.4.2. We can easily adjust for the difference. Compare the tables between the two examples and adjust accordingly

From Example $8.4.2$
$n =$ figure number	$a_n =$ # of circles
$1$	$1$
$2$	$3$
$3$	$6$
$4$	$10$
$n$	$\dfrac{n(n+1)}{2}$

Use Example 8.4.2 as a model for finding the formula for Example 8.4.3. The $n$-values of Example 8.4.2 are one less than the $n$-values of Example 8.4.3.

From Example $8.4.3$
$n =$ class size	$b_n =$ handshakes
$2$	$1$
$3$	$3$
$4$	$6$
$5$	$10$
$n$	Formula?

Since we know the formula for Example 8.4.2, let’s adjust the $n$−values of Example $8.4.3$ to match Example 8.4.2. Since we are matching Example 8.4.3 to Example 8.4.2, we need to subtract one from the $n$-value. In essence, the value of $b_n$ of Example 8.4.3 (handshakes) matches the value of $a_{n-1}$ for Example 8.4.2 (number of circles).

$b_{25}$of Example 8.4.3 is the same as $a_{24}$ of Example 8.4.2.

An important skill for problem solving is to use work that has already been achieved. Not every problem is a fresh slate.

$\begin{array}& a_{24} &= \dfrac{24(24+1)}{2} &\text{Substitute \(n = 24$ in the formula for Example 8.4.2.}\\ a_{24} &= \dfrac{24(25)}{2} &\text{Simplify the parentheses first.} \\ a_{24} &= \dfrac{600}{2} &\text{Simplify the numerator. Then divide.} \\ a_{24} &= 300 &\text{But now apply this answer to Example 8.4.3: $b_{25} = 300$.} \end{array}\)

To find the formula, $a_n$, for Example 8.4.3, substitute $(n − 1)$ for $n$ in Example 8.4.2.

Formula for Example 8.4.3:

$\begin{array} && \dfrac{(\textcolor{red}{n−1})[(\textcolor{red}{n−1})+1]}{2} &\text{Replace each \(n$ with $(n − 1)$ in the formula of Example 8.4.2.} \\ &\dfrac{(n−1)n}{2} &\text{Simplify within parentheses.} \\ &\dfrac{n(n−1)}{2} &\text{This is the formula for Example 8.4.3.} \\ &b_{25} = \dfrac{25(24)}{2} &\text{Verify that we get the same answer, $300$, as above.} \\ &b_{25} = 300 & \end{array}\)

Answer In Jerome’s class of $25$ students, there would be $300$ different handshakes if each student shook hands with every other student.

Try It! (Exercises)

For #1-3, the general term of the sequence is given.

a. State the first five terms, starting with $n = 1$.

b. Find the value $a_{12}$.

$a_n = n^2 + n − 1$
$a_n = 2(n + 1) 2$
$a_n = 2n^2 + 2$

For #4-8, Let $s_n =$ The sum of the first $n$ consecutive natural numbers. Find the value indicated.

$s_{32}$
$s_{80}$
$s_{100}$
$s_{201}$
$s_{496}$

For #9-13, A room has $n$ people, all of whom will shake hands once with every other person in the room. Let $b_n =$ number of different handshakes. Find the value indicated.

$b_{16}$
$b_{36}$
$b_{52}$
$b_{100}$
$b_{229}$
Find the sum of the first $30$ odd numbers.
Use the fact that $2 + 4 + 6 + 8 + ⋯ = 2(1 + 2 + 3 + 4 + ⋯ )$ to find the sum of the first $50$ even numbers.
Write a formula to describe the sum of the first $n$ number of even numbers.

For #17-21, A pattern of figures is shown below. Let $a_n =$ the number of small square tiles used to create figure $n$. Find the value indicated.

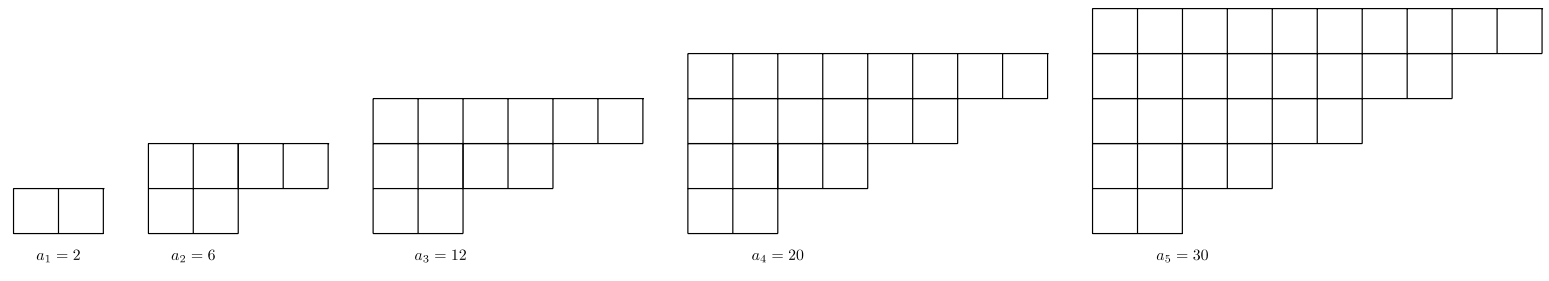
$clipboard_ec28104a668a2c53146a30feee403d95d.png$

$a_{6}$
$a_{8}$
$a_{22}$
$a_{60}$
The formula $a_n$.

For #22-24, first determine the number of matchsticks in each Figure 1-4. Let $a_n =$ the number of matchsticks in figure $n$. Find the value indicated.

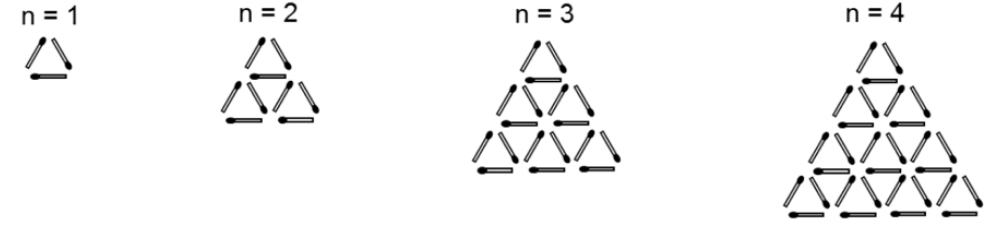
$clipboard_ee9c10f82919a4bb25777d617860c0615.png$

$a_5$
Find $a_n$ given that $a_n = \dfrac{3n(n+k)}{2}$ for some $k$.
$a_{45}$

For #25-27, the $4$ polygons below demonstrate how to count diagonals within each polygon. A diagonal (shown in blue) is the connection of non-neighboring vertices. Let $p_n =$ the number of diagonals in any $n$−sided figure. Find the value indicated.

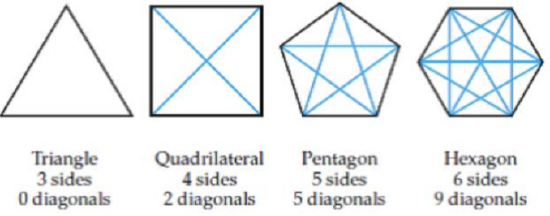
$clipboard_e32128b40b8cb3908f1c93e61ec0747aa.png$

$p_7$
Given that $p_n = \dfrac{n(n−k)}{2}$ for some $k$, Find $k$ and $p_n$.
$p_{40}$

For #28-30, refer to the experiment with gravity described below:

You are curious if there is a relationship between the number of feet a ball drops from a balcony $144$ feet above ground. You set up a camera to take a burst of photographs every second as a ball falls in front of a height chart. You create the following table based on the photographs:

Time (sec)	$0$	$1$	$2$	$3$
Distance (feet)	$0$	$16$	$64$	$144$

You reason that the ball’s distance is a quadratic sequence. How did you know?
After graphing the points, you reason that the sequence has general term $d_t = kt^2$ where $t =$ time in seconds and $k$ is a real number. Determine the value of $k$, then find $d_t$.
Using your answers to #28 and #29, suppose you were standing at the top of a cliff for which you did not know the height. You dropped a rock from the top. $6$ seconds later, you heard the rock hit the ground. How high above the ground are you?

For #31-33, use the table to describe the lift of airplanes:

For a given wing area, the lift of an airplane is proportional to the square of its speed.

Let $s =$ speed of airplane. Then $l_s = ks^2$ for some constant, $k$.

The table below shows the lift for a Boeing 737 airplane at various speeds.

Speed (mph)	$0$	$75$	$150$	$225$	$300$	$375$
Lift ($1000$s of pound)	$0$	$25$	$100$	$225$	$400$	$625$

You reason that the lift of an airplane is a quadratic sequence. How did you know?
After graphing the points, you reason that the sequence has general term $l_s = ks^2$ where $s =$ speed in mph and $k$ is a constant. Determine the value of $k$, then find $l_s$.
Use your answers to #31 and #32 to find the lift for an airplane that is traveling $425$ mph.

\(n =\) class size	\(b_n =\) handshakes
\(2\)	\(1\)
\(3\)	\(3\)
\(4\)	\(6\)
\(5\)	\(10\)

From Example \(8.4.2\)
\(n =\) figure number	\(a_n =\) # of circles
\(1\)	\(1\)
\(2\)	\(3\)
\(3\)	\(6\)
\(4\)	\(10\)
\(n\)	\(\dfrac{n(n+1)}{2}\)

From Example \(8.4.3\)
\(n =\) class size	\(b_n =\) handshakes
\(2\)	\(1\)
\(3\)	\(3\)
\(4\)	\(6\)
\(5\)	\(10\)
\(n\)	Formula?

Time (sec)	\(0\)	\(1\)	\(2\)	\(3\)
Distance (feet)	\(0\)	\(16\)	\(64\)	\(144\)

Speed (mph)	\(0\)	\(75\)	\(150\)	\(225\)	\(300\)	\(375\)
Lift (\(1000\)s of pound)	\(0\)	\(25\)	\(100\)	\(225\)	\(400\)	\(625\)