5.E: Graphing and Inverse Functions (Exercises)

Last updated
Save as PDF

Page ID: 3332

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

These are homework exercises to accompany Corral's "Elementary Trigonometry" Textmap. This is a text on elementary trigonometry, designed for students who have completed courses in high-school algebra and geometry. Though designed for college students, it could also be used in high schools. The traditional topics are covered, but a more geometrical approach is taken than usual. Also, some numerical methods (e.g. the secant method for solving trigonometric equations) are discussed.

5.1 Exercise

For Exercises 1-12, draw the graph of the given function for $0 \le x \le 2\pi $.

5.1.1 $y=-\cos\;x$

5.1.2 $y=1+\sin\;x$

5.1.3 $y=2-\cos\;x$

5.1.4 $y=2-\sin\;x$

5.1.5 $y=-\tan\;x$

5.1.6 $y=-\cot\;x$

5.1.7 $y=1+\sec\;x$

5.1.8 $y=-1-\csc\;x$

5.1.9 $y=2\sin\;x$

5.1.10 $y=-3\cos\;x$

5.1.11 $y=-2\tan\;x$

5.1.12 $y=-2\sec\;x$

5.1.13 We can extend the unit circle definition of the sine and cosine functions to all six trigonometric functions. Let $P $ be a point in QI on the unit circle, so that the line segment $\overline{OP} $ in Figure 5.1.10 has length $1 $ and makes an acute angle $\theta$ with the positive $x$-axis. Identify each of the six trigonometric functions of $\theta $ with exactly one of the line segments in Figure 5.1.10, keeping in mind that the radius of the circle is $1 $. To get you started, we have $\sin\;\theta = MP $ (why?).

$alt$
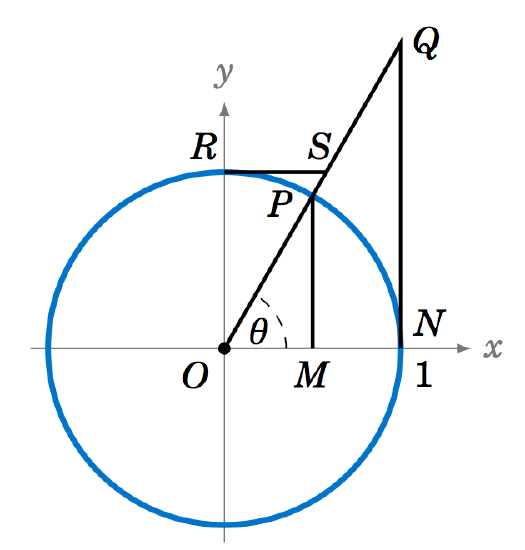
Figure 5.1.10

5.1.14 For Exercise 13, how would you draw the line segments in Figure 5.1.10 if $\theta $ was in QII? Recall that some of the trigonometric functions are negative in QII, so you will have to come up with a convention for how to treat some of the line segment lengths as negative.

5.1.15 For any point $(x,y) $ on the unit circle and any angle $\alpha $, show that the point $R_{\alpha} (x,y) $ defined by $R_{\alpha} (x,y) = (x\,\cos\;\alpha \,-\, y\,\sin\;\alpha , x\,\sin\;\alpha \,+\, y\,\cos\;\alpha) $ is also on the unit circle. What is the geometric interpretation of $R_{\alpha} (x,y)$? Also, show that $R_{-\alpha} (R_{\alpha} (x,y)) = (x,y) $ and $R_{\beta} (R_{\alpha} (x,y)) = R_{\alpha + \beta} (x,y) $.

5.2 Exercise

For Exercises 1-12, find the amplitude, period, and phase shift of the given function. Then graph one cycle of the function, either by hand or by using Gnuplot (see Appendix B).

5.2.1 $y=3\,\cos\;\pi x$

5.2.2 $y=\sin\;(2\pi x - \pi)$

5.2.3 $y=-\sin\;(5x + 3)$

5.2.4 $y=1+8\,\cos\;(6x- \pi)$

5.2.5 $y=2+\cos\;(5x + \pi)$

5.2.6 $y=1-\sin\;(3\pi - 2x)$

5.2.7 $y=1-\cos\;(3\pi - 2x)$

5.2.8 $y=2\,\tan\;(x - 1)$

5.2.9 $y=1-\tan\;(3\pi - 2x)$

5.2.10 $y=\sec\;(2x + 1)$

5.2.11 $y=2\csc\;(2x - 1)$

5.2.12 $y=2+4\,\cot\;(1-x)$

5.2.13 For the function $y=2\,\sin\;( x^2 ) $ in Example 5.8, for which values of $x$ does the function reach its maximum value $2 $, and for which values of $x $ does it reach its minimum value $-2\,$?

5.2.14 For the function $y=3\,\sin\;x + 4\,\cos\;x $ in Example 5.9, for which values of $x $ does the function reach its maximum value $5 $, and for which values of $x $ does it reach its minimum value $-5\,$? You can restrict your answers to be between $0 $ and $2\pi $.

5.2.15 Graph the function $y=\sin^2 \,x $ from $x=0 $ to $x=2\pi $, either by hand or by using Gnuplot. What are the amplitude and period of this function?

5.2.16 The current $i(t) $ in an AC electrical circuit at time $t\ge 0 $ is given by $i(t) = I_m \,\sin\;\omega t $, and the voltage $v(t) $ is given by $v(t) = V_m \,\sin\;\omega t $, where $V_m > I_m > 0 $ and $\omega > 0 $ are constants. Sketch one cycle of both $i(t) $ and $v(t) $ together on the same graph (i.e. on the same set of axes). Are the current and voltage in phase or out of phase?

5.2.17 Repeat Exercise 16 with $i(t) $ the same as before but with $v(t)= V_m \,\sin\;\left(\omega t + \frac{\pi}{4}\right) $.

5.2.18 Repeat Exercise 16 with $i(t)=-I_m \,\cos\;\left(\omega t - \frac{\pi}{3}\right) $ and $v(t)=
V_m \,\sin\;\left(\omega t - \frac{5\pi}{6}\right) $.

For Exercises 19-21, find the amplitude and period of the given function. Then graph one cycle of the function, either by hand or by using Gnuplot.

5.2.19 $y=3\,\sin\;\pi x \;-\; 5\,\cos\;\pi x$

5.2.20 $y=-5\,\sin\;3x \;+\; 12\,\cos\;3x$

5.2.21 $y=2\,\cos\;x \;+\; 2\,\sin\;x$

5.2.22 Find the amplitude of the function $y=2\,\sin\;( x^2 ) \;+\; \cos\;( x^2 ) $.

For Exercises 23-25, find the period of the given function. Graph one cycle using Gnuplot.

5.2.23 $y=\sin\;3x \;-\; \cos\;5x$

5.2.24 $y=\sin\;\frac{x}{3} \;+\; 2\,\cos\;\frac{3x}{4}$

5.2.25 $y=2\,\sin\;\pi x \;+\; 3\,\cos\;\frac{\pi}{3}x$

5.2.26 Let $y = 0.5\,\sin\;x ~\sin\;12x\, $. Its graph for $x $ from $0 $ to $4\pi $ is shown in Figure 5.2.14:

$alt$
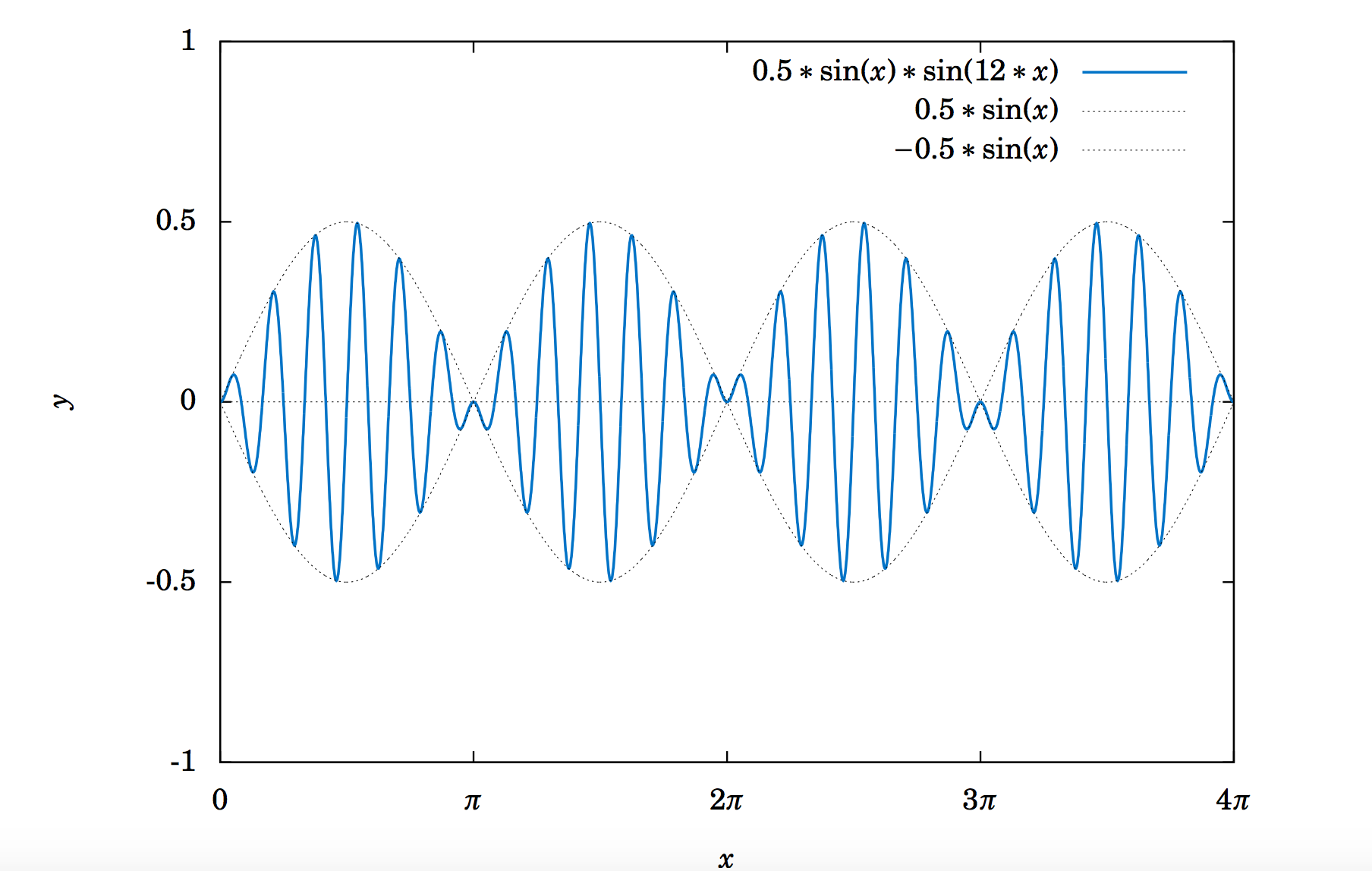
Figure 5.2.14 Modulated wave $y = 0.5 \sin x \sin 12x$

You can think of this function as $\sin\;12x $ with a sinusoidally varying "amplitude''of $0.5\,\sin\;x $. What is the period of this function? From the graph it looks like the amplitude may be $0.5 $. Without finding the exact amplitude, explain why the amplitude is in fact less than $0.5 $. The function above is known as a modulated wave, and the functions $\pm\,0.5\,\sin\;x $ form an amplitude envelope for the wave (i.e. they enclose the wave). Use an identity from Section 3.4 to write this function as a sum of sinusoidal curves.

5.2.27 Use Gnuplot to graph the function $y= x^2 \,\sin\;10x $ from $x = -2\pi $ to $x=2\pi $. What functions form its amplitude envelope? (Note: Use $\texttt{set samples 500}$ in Gnuplot.)

5.2.28 Use Gnuplot to graph the function $y= \frac{1}{x^2} \,\sin\;80x $ from $x = 0.2 $ to $x=\pi $. What functions form its amplitude envelope? (Note: Use $\texttt{set samples 500}$ in Gnuplot.)

5.2.29 Does the function $y=\sin\;\pi x \;+\; \cos\;x $ have a period? Explain your answer.

5.2.30 Use Gnuplot to graph the function $y=\frac{\sin\;x}{x} $ from $x=-4\pi $ to $x=4\pi $. What happens at $x=0$?

5.3 Exercise

For Exercises 1-25, find the exact value of the given expression in radians.

5.3.1 $\tan^{-1} 1$

5.3.2 $\tan^{-1} \,(-1)$

5.3.3 $\tan^{-1} 0$

5.3.4 $\cos^{-1} 1$

5.3.5 $\cos^{-1} \,(-1)$

5.3.6 $\cos^{-1} 0$

5.3.7 $\sin^{-1} 1$

5.3.8 $\sin^{-1} \,(-1)$

5.3.9 $\sin^{-1} 0$

5.3.10 $\sin^{-1} \left(\sin\;\frac{\pi}{3}\right)$

5.3.11 $\sin^{-1} \left(\sin\;\frac{4\pi}{3}\right)$

5.3.12 $\sin^{-1} \left(\sin\;\left(-\frac{5\pi}{6}\right)\right)$

5.3.13 $\cos^{-1} \left(\cos\;\frac{\pi}{7}\right)$

5.3.14 $\cos^{-1} \left(\cos\;\left(-\frac{\pi}{10}\right)\right)$

5.3.15 $\cos^{-1} \left(\cos\;\frac{6\pi}{5}\right)$

5.3.16 $\tan^{-1} \left(\tan\;\frac{4\pi}{3}\right)$

5.3.17 $\tan^{-1} \left(\tan\;\left(-\frac{5\pi}{6}\right)\right)$

5.3.18 $\cot^{-1} \left(\cot\;\frac{4\pi}{3}\right)$

5.3.19 $\csc^{-1} \left(\csc\;\left(-\frac{\pi}{9}\right)\right)$

5.3.20 $\sec^{-1} \left(\sec\;\frac{6\pi}{5}\right)$

5.3.21 $\cos\;\left(\sin^{-1}\;\left(\frac{5}{13}\right)\right)$

5.3.22 $\cos\;\left(\sin^{-1}\;\left(-\frac{4}{5}\right)\right)$

5.3.23 $\sin^{-1}\;\frac{3}{5} \;+\; \sin^{-1}\;\frac{4}{5}$

5.3.24 $\sin^{-1}\;\frac{5}{13} \;+\; \cos^{-1}\;\frac{5}{13}$

5.3.25 $\tan^{-1}\;\frac{3}{5} \;+\; \cot^{-1}\;\frac{3}{5}$

For Exercises 26-33, prove the given identity.

5.3.26 $\cos\;(\sin^{-1} x) ~=~ \sqrt{1 - x^2}$

5.3.27 $\sin\;(\cos^{-1} x) ~=~ \sqrt{1 - x^2}$

5.3.28 $\sin^{-1} x \;+\; \cos^{-1} x ~=~ \frac{\pi}{2}$

5.3.29 $\sec^{-1} x \;+\; \csc^{-1} x ~=~ \frac{\pi}{2}$

5.3.30 $\sin^{-1} (-x) ~=~ -\sin^{-1} x$

5.3.31 $\cos^{-1} (-x) \;+\; \cos^{-1} x ~=~ \pi$

5.3.32 $\cot^{-1} x ~=~ \tan^{-1} \,\frac{1}{x}~ $ for $x>0$

5.3.33 $\tan^{-1} x \;+\; \tan^{-1} \,\frac{1}{x} ~=~ \frac{\pi}{2}~ $ for $x>0$

5.3.34 In Example 5.22 we showed that the formula $\;\tan^{-1} a \;+\; \tan^{-1} b ~=~ \tan^{-1} \left( \dfrac{a+b}{1-ab} \right)\; $ does not always hold. Does the formula $\tan\;(\tan^{-1} a \;+\; \tan^{-1} b ) ~=~ \dfrac{a+b}{1-ab} $, which was part of that example, always hold? Explain your answer.

5.3.35 Show that $\;\tan^{-1}\;\frac{1}{3}\;+\;\tan^{-1}\;\frac{1}{5} ~=~ \tan^{-1}\;\frac{4}{7}\; $.

5.3.36 Show that $\;\tan^{-1}\;\frac{1}{4}\;+\;\tan^{-1}\;\frac{2}{9} ~=~ \tan^{-1}\;\frac{1}{2}\; $.

5.3.37 Figure 5.3.13 shows three equal squares lined up against each other. For the angles $\alpha $, $\beta $, and $\gamma $ in the picture, show that $\alpha = \beta + \gamma $. (Hint: Consider the tangents of the angles.)

$alt$
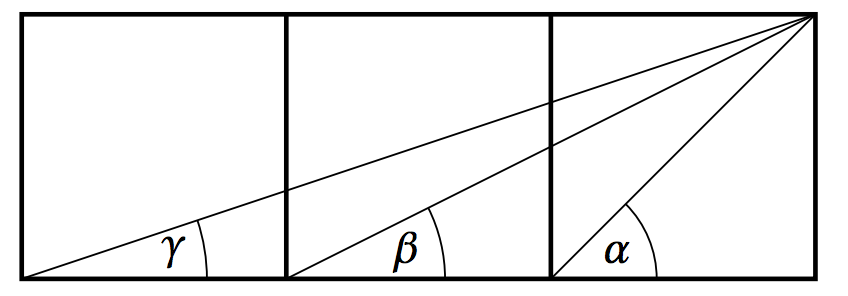
Figure 5.3.13 Exercise 37

5.3.38 Sketch the graph of $y=\sin^{-1} 2x $.

5.3.39 Write a computer program to solve a triangle in the case where you are given three sides. Your program should read in the three sides as input parameters and print the three angles in degrees as output if a solution exists. Note that since most computer languages use radians for their inverse trigonometric functions, you will likely have to do the conversion from radians to degrees yourself in the program.

Search

Text Color

Text Size

Margin Size

Font Type

5.1 Exercise

5.2 Exercise

5.3 Exercise