1.E: Functions (Exercises)
- Page ID
- 9155
This page is a draft and is under active development.
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1.1: Functions and Function Notation
A jetliner changes altitude as its distance from the starting point of a flight increases. The weight of a growing child increases with time. In each case, one quantity depends on another. There is a relationship between the two quantities that we can describe, analyze, and use to make predictions. In this section, we will analyze such relationships.
Verbal
1) What is the difference between a relation and a function?
- Answer
-
A relation is a set of ordered pairs. A function is a special kind of relation in which no two ordered pairs have the same first coordinate.
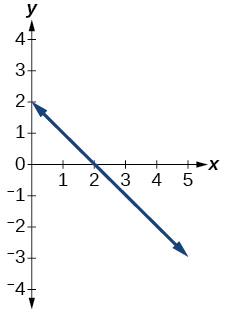
2) What is the difference between the input and the output of a function?
3) Why does the vertical line test tell us whether the graph of a relation represents a function?
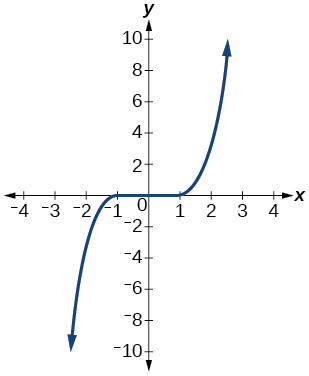
- Answer
-
When a vertical line intersects the graph of a relation more than once, that indicates that for that input there is more than one output. At any particular input value, there can be only one output if the relation is to be a function.
4) How can you determine if a relation is a one-to-one function?
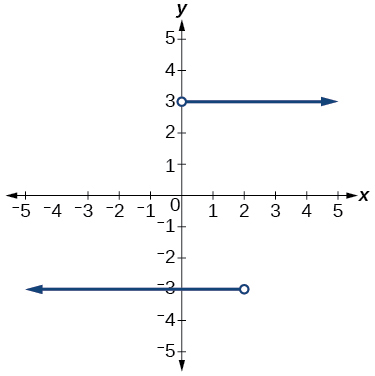
5) Why does the horizontal line test tell us whether the graph of a function is one-to-one?
- Answer
-
When a horizontal line intersects the graph of a function more than once, that indicates that for that output there is more than one input. A function is one-to-one if each output corresponds to only one input.
Algebraic
For the exercises 6-7, determine whether the relation represents a function.
6) \(\{(a,b), (c,d), (a,c)\}\)
7) \(\{(a,b),(b,c),(c,c)\}\)
- Answer
-
function
For the exercises 8-26, determine whether the relation represents \(y\) as a function of \(x\).
8) \(5x+2y=10\)
9) \(y=x^2\)
- Answer
-
function
10) \(x=y^2\)
11) \(3x^2+y=14\)
- Answer
-
function
12) \(2x+y^2=6\)
13) \(y=−2x^2+40x\)
- Answer
-
function
14) \(y=\dfrac{1}{x}\)
15) \(x=\dfrac{3y+5}{7y−1}\)
- Answer
-
function
16) \(x=\sqrt{1−y^2}\)
17) \(y=\dfrac{3x+5}{7x−1}\)
- Answer
-
function
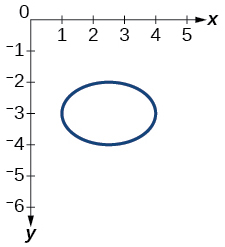
18) \(x^2+y^2=9\)
19) \(2xy=1\)
- Answer
-
function
20) \(x=y^3\)
21) \(y=x^3\)
- Answer
-
function
22) \(y=\sqrt{1−x^2}\)
23) \(x=\pm\sqrt{1-y}\)
- Answer
-
function
24) \(y=\pm\sqrt{1−x}\)
25) \(y^2=x^2\)
- Answer
-
not a function
26) \(y^3=x^2\)
For the exercises 27-39, evaluate the function \(f\) at the indicated values \(f(−3),f(2),f(−a),−f(a),f(a+h)\).
27) \(f(x)=2x−5\)
- Answer
-
\(f(−3)=−11\); \(f(2)=−1\); \(f(−a)=−2a−5\); \(−f(a)=−2a+5\); \(f(a+h)=2a+2h−5\)
28) \(f(x)=−5x^2+2x−1\)
29) \(f(x)=\sqrt{2−x}+5\)
- Answer
-
\(f(−3)=\sqrt{5+5}\); \(f(2)=5\); \(f(−a)=\sqrt{2+a+5}\); \(−f(a)=−\sqrt{2−a}−5\); \(f(a+h)=\sqrt{2−a−h}+5\)
30) \(f(x)=\dfrac{6x−1}{5x+2}\)
31) \(f(x)=|x−1|−|x+1|\)
- Answer
-
\(f(−3)=2\); \(f(2)=1−3=−2\); \(f(−a)=|−a−1|−|−a+1|\); \(−f(a)=−|a−1| +|a+1|\); \(f(a+h)= |a+h−1|−|a+h+1|\)
32) Given the function \(g(x)=5−x^2\), evaluate \(g(x+h)−g(x)h\), \(h{\neq}0\).
33) Given the function \(g(x)=x^2+2x\), evaluate \(\dfrac{g(x)−g(a)}{x−a}\), \(x{\neq}a\).
- Answer
-
\(\dfrac{g(x)−g(a)}{x−a}=x+a+2\), \(x{\neq}a\)
34) Given the function \(k(t)=2t−1\):
a. Evaluate \(k(2)\).
b. Solve \(k(t)=7\).
35) Given the function \(f(x)=8−3x\):
a. Evaluate \(f(−2)\).
b. Solve \(f(x)=−1\).
- Answer
-
a. \(f(−2)=14\); b. \(x=3\)
36) Given the function \(p(c)=c^2+c\):
a. Evaluate \(p(−3)\).
b. Solve \(p(c)=2\).
37) Given the function \(f(x)=x^2−3x\):
a. Evaluate \(f(5)\).
b. Solve \(f(x)=4\).
- Answer
-
a. \(f(5)=10\); b. \(x=−1\) or \(x=4\)
38) Given the function \(f(x)=\sqrt{x+2}\):
a. Evaluate \(f(7)\).
b. Solve \(f(x)=4\).
39) Consider the relationship \(3r+2t=18\).
a. Write the relationship as a function \(r=f(t)\).
b. Evaluate \(f(−3)\).
c. Solve \(f(t)=2\).
- Answer
-
a. \(f(t)=6−\frac{2}{3}t\); b. \(f(−3)=8\); c. \(t=6\)
Graphical
For the exercises 40-54, use the vertical line test to determine which graphs show relations that are functions.
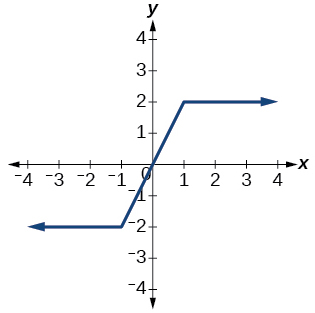
40)
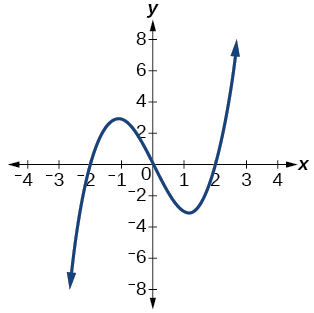
41)
- Answer
-
not a function
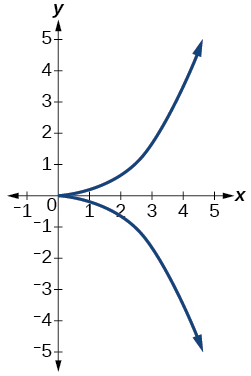
42)
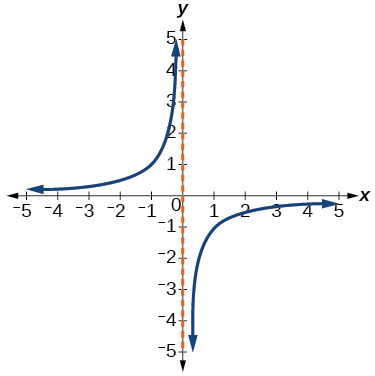
43)
- Answer
-
function
44)
45)
- Answer
-
function
46)
47)
- Answer
-
function
48)
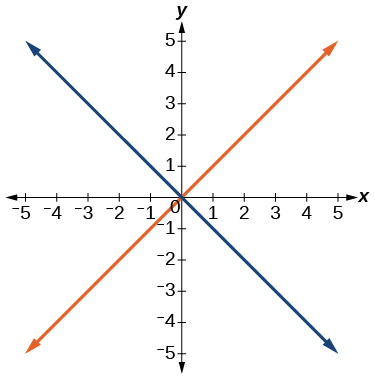
49)
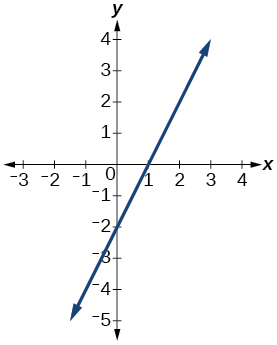
- Answer
-
function
50)
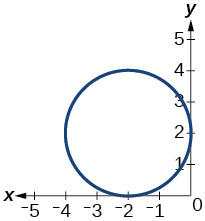
51)
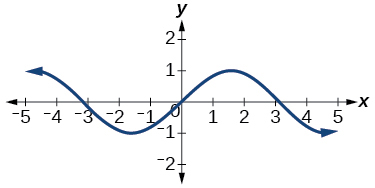
- Answer
-
function
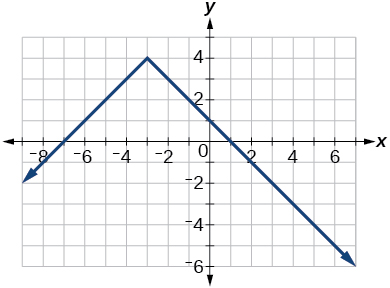
52) Given the following graph,
- Evaluate \(f(−1)\).
- Solve for \(f(x)=3\).
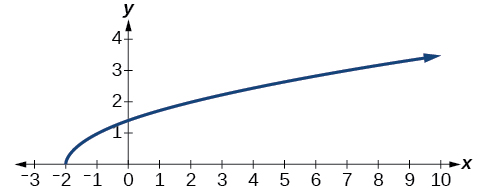
53) Given the following graph,
- Evaluate \(f(0)\).
- Solve for \(f(x)=−3\).
- Answer
-
a.\(f(0)=1\); b. \(f(x)=−3\), \(x=−2\) or \(x=2\)
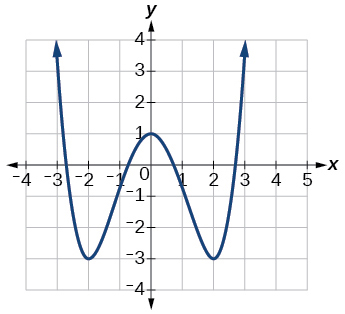
54) Given the following graph,
- Evaluate \(f(4)\).
- Solve for \(f(x)=1\).
For the exercises 55-59, determine if the given graph is a one-to-one function.
55)
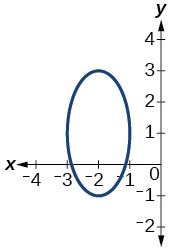
- Answer
-
not a function so it is also not a one-to-one function
56)
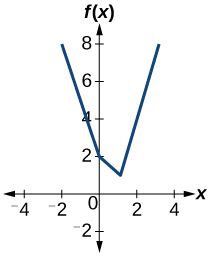
57)
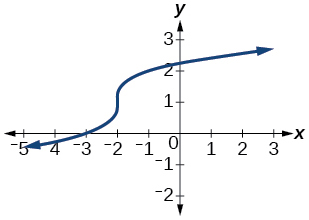
- Answer
-
one-to-one function
58)
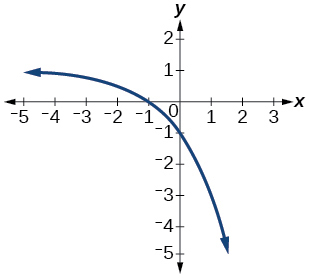
59)
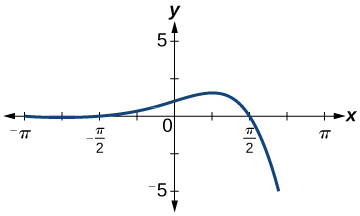
- Answer
-
function, but not one-to-one
Numeric
For the exercises 60-62, determine whether the relation represents a function.
60) \(\{(−1,−1),(−2,−2),(−3,−3)\}\)
61) \(\{(3,4),(4,5),(5,6)\}\)
- Answer
-
function
62) \((2,5),(7,11),(15,8),(7,9)\}\)
For the exercises 63-65, determine if the relation represented in table form represents \(y\) as a function of \(x\).
63)
| \(x\) | 5 | 10 | 15 |
|---|---|---|---|
| \(y\) | 3 | 8 | 14 |
- Answer
-
function
64)
| \(x\) | 5 | 10 | 15 |
|---|---|---|---|
| \(y\) | 3 | 8 | 8 |
65)
| \(x\) | 5 | 10 | 10 |
|---|---|---|---|
| \(y\) | 3 | 8 | 14 |
- Answer
-
not a function
For the exercises 66-67, use the function \(f\) represented in the Table below
| \(x\) | \(f(x)\) |
|---|---|
| 0 | 74 |
| 1 | 28 |
| 2 | 1 |
| 3 | 53 |
| 4 | 56 |
| 5 | 3 |
| 6 | 36 |
| 7 | 45 |
| 8 | 14 |
| 9 | 47 |
66) Evaluate \(f(3)\).
67) Solve \(f(x)=1\).
- Answer
-
\(f(x)=1\), \(x=2\)
For the exercises 68-73, evaluate the function \(f\) at the values \(f(−2)\), \(f(−1)\), \(f(0)\), \(f(1)\),and \(f(2)\).
68) \(f(x)=4−2x\)
69) \(f(x)=8−3x\)
- Answer
-
\(f(−2)=14\);\(f(−1)=11\);\(f(0)=8\);\(f(1)=5\);\(f(2)=2\)
70) \(f(x)=8x^2−7x+3\)
71) \(f(x)=3+\sqrt{x+3}\)
- Answer
-
\(f(−2)=4\); \(f(−1)=4.414\); \(f(0)=4.732\); \(f(1)=4.5\); \(f(2)=5.236\)
72) \(f(x)=\dfrac{x-2}{x+3}\)
73) \(f(x)=3^x\)
- Answer
-
\(f(−2)=\frac{1}{9}\); \(f(−1)=\frac{1}{3}\); \(f(0)=1\); \(f(1)=3\); \(f(2)=9\)
For the exercises 74-75, evaluate the expressions, given functions \(f\), \(g\), and \(h\):
- \(f(x)=3x−2\)
- \(g(x)=5−x^2\)
- \(h(x)=−2x^2+3x−1\)
74) \(3f(1)−4g(−2)\)
75) \(f \left (\dfrac{7}{3} \right )−h(−2)\)
- Answer
-
\(20\)
Technology
For the exercises 76-78, graph \(y=x^2\) on the given viewing window. Determine the corresponding range for each viewing window. Show each graph.
76) \([−0.1, 0.1]\)
77) \([−10, 10]\)
- Answer
-
\([0, 100]\)
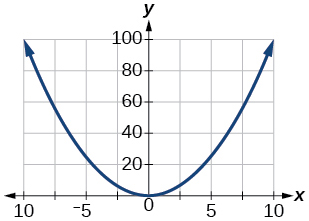
78) \([−100,100]\)
For the exercises 79-81, graph \(y=x^3\) on the given viewing window. Determine the corresponding range for each viewing window. Show each graph.
79) \([−0.1, 0.1]\)
- Answer
-
\([−0.001, 0.001]\)
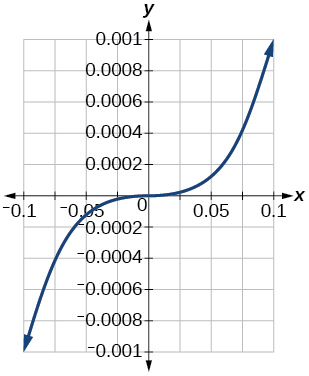
80) \([−10, 10]\)
81) \([−100, 100]\)
- Answer
-
\([−1,000,000, 1,000,000]\)
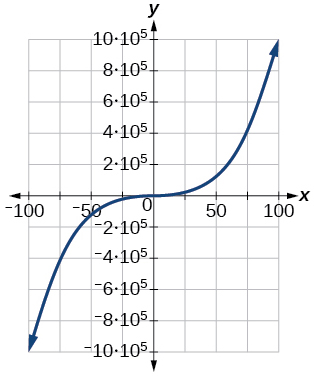
For the exercises 82-84, graph \(y=\sqrt{x}\) on the given viewing window. Determine the corresponding range for each viewing window. Show each graph.
82) \([0, 0.01]\)
83) \([0, 100]\)
- Answer
-
\([0, 10]\)
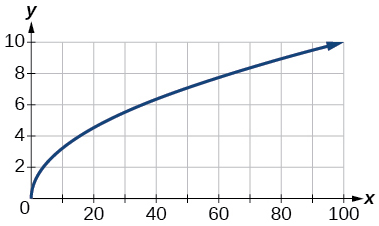
84) \([0, 10,000]\)
For the exercises 85-87, graph \(y=\sqrt[3]{x}\) on the given viewing window. Determine the corresponding range for each viewing window. Show each graph.
85) \([−0.001,0.001]\)
- Answer
-
\([−0.1,0.1]\)
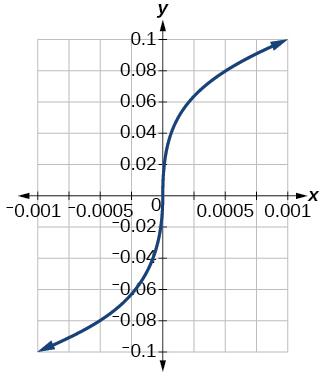
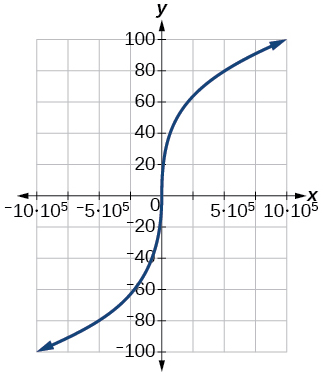
86) \([−1000,1000]\)
87) \([−1,000,000,1,000,000]\)
- Answer
-
\([−100, 100]\)
Real-World Applications
88) The amount of garbage, \(G\), produced by a city with population \(p\) is given by \(G=f(p)\). \(G\) is measured in tons per week, and \(p\) is measured in thousands of people.
The town of Tola has a population of \(40,000\) and produces \(13\) tons of garbage each week. Express this information in terms of the function \(f\).Tola has a population of \(40,000\) and produces \(13\) tons of garbage each week. Express this information in terms of the function \(f\).
Explain the meaning of the statement \(f(5)=2\).
89) The number of cubic yards of dirt, \(D\), needed to cover a garden with area a square feet is given by \(D=g(a)\).
a. A garden with area \(5000\) \(ft^2\) requires \(50\) \(yd^3\) of dirt. Express this information in terms of the function \(g\).
b. Explain the meaning of the statement \(g(100)=1\).
- Answer
-
a. \(g(5000)=50\); b. The number of cubic yards of dirt required for a garden of \(100\) square feet is \(1\).
90) Let \(f(t)\) be the number of ducks in a lake \(t\) years after 1990. Explain the meaning of each statement:
a. f(5)=30
b. f(10)=40
91) Let \(h(t)\) be the height above ground, in feet, of a rocket \(t\) seconds after launching. Explain the meaning of each statement:
a. \(h(1)=200\)
b. \(h(2)=350\)
- Answer
-
a. The height of a rocket above ground after \(1\) second is \(200\) ft. b. the height of a rocket above ground after \(2\) seconds is \(350\) ft.
92) Show that the function \(f(x)=3(x−5)^2+7\) is not one-to-one.
1.2: Domain and Range
In creating various functions using the data, we can identify different independent and dependent variables, and we can analyze the data and the functions to determine the domain and range. In this section, we will investigate methods for determining the domain and range of functions.
Verbal
1) Why does the domain differ for different functions?
- Answer
-
The domain of a function depends upon what values of the independent variable make the function undefined or imaginary.
2) How do we determine the domain of a function defined by an equation?
3) Explain why the domain of \(f(x)=\sqrt[3]{x}\) is different from the domain of \(f(x)=\sqrt{x}\).
- Answer
-
There is no restriction on x for \(f(x)=\sqrt[3]{x}\) because you can take the cube root of any real number. So the domain is all real numbers, \((−∞,∞)\). When dealing with the set of real numbers, you cannot take the square root of negative numbers. So x-values are restricted for \(f(x)=\sqrt{x}\) to nonnegative numbers and the domain is \([0,∞)\).
4) When describing sets of numbers using interval notation, when do you use a parenthesis and when do you use a bracket?
5) How do you graph a piecewise function?
- Answer
-
Graph each formula of the piecewise function over its corresponding domain. Use the same scale for the x-axis and y-axis for each graph. Indicate inclusive endpoints with a solid circle and exclusive endpoints with an open circle. Use an arrow to indicate \(−∞\) or \(∞\). Combine the graphs to find the graph of the piecewise function.
Algebraic
For the exercises 6-25, find the domain of each function using interval notation.
6) \(f(x)=−2x(x−1)(x−2)\)
7) \(f(x)=5−2x^2\)
- Answer
-
\((-\infty,\infty)\)
8) \(f(x)=3\sqrt{x-2}\)
9) \(f(x)=3-\sqrt{6-2x}\)
- Answer
-
\(\left(-\infty,3\right]\)
10) \(f(x)=\sqrt{4-3x}\)
11) \(f(x)=\sqrt{x^2+4}\)
- Answer
-
\((-\infty,\infty)\)
12) \(f(x)=\sqrt[3]{1-2x}\)
13) \(f(x)=\sqrt[3]{x-1}\)
- Answer
-
\((-\infty,\infty)\)
14) \(f(x)=\dfrac{9}{x-6}\)
15) \(f(x)=\dfrac{3x+1}{4x+2}\)
- Answer
-
\(\left (-\infty,-\dfrac{1}{2} \right )\cup \left (-\dfrac{1}{2},\infty \right )\)
16) \(f(x)=\dfrac{\sqrt{x+4}}{x-4}\)
17) \(f(x)=\dfrac{x-3}{x^2+9x-22}\)
- Answer
-
\((-\infty,-11)\cup(-11,2)\cup(2,\infty)\)
18) \(f(x)=\dfrac{1}{x^2-x-6}\)
19) \(f(x)=\dfrac{2x^3−250}{x^2−2x−15}\)
- Answer
-
\((-\infty,-3)\cup(-3,5)\cup(5,\infty)\)
20) \(\dfrac{5}{\sqrt{x-3}}\)
21) \(\dfrac{2x+1}{\sqrt{5-x}}\)
- Answer
-
\((-\infty,5)\)
22) \(\dfrac{\sqrt{x-4}}{\sqrt{x-6}}\)
23) \(\dfrac{\sqrt{x-6}}{\sqrt{x-4}}\)
- Answer
-
\(\left[6,\infty\right)\)
24) \(f(x)=\dfrac{x}{x}\)
25) \(f(x)=\dfrac{x^2-9x}{x^2-81}\)
- Answer
-
\((-\infty,-9)\cup(-9,9)\cup(9,\infty)\)
26) Find the domain of the function \(f(x)=\sqrt{2x^3-50x}\) by:
a. using algebra
b. graphing the function in the radicand and determining intervals on the x-axis for which the radicand is nonnegative.
Graphical
For the exercises 27-37, write the domain and range of each function using interval notation.
27)
![Graph of a function from \(\left(2, 8\right]\).](https://math.libretexts.org/@api/deki/files/1092/CNX_Precalc_Figure_01_02_202.jpg?revision=1&size=bestfit&width=200&height=200)
- Answer
-
domain: \(\left(2,8\right]\), range \(\left[6,8\right)\)
28)
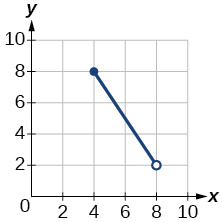
29)
![Graph of a function [-4,4]](https://math.libretexts.org/@api/deki/files/1094/CNX_Precalc_Figure_01_02_204.jpg?revision=1&size=bestfit&width=300&height=175)
- Answer
-
domain: \([−4, 4]\), range: \([0, 2]\)
30)
![Graph of a function [2,6]](https://math.libretexts.org/@api/deki/files/1095/CNX_Precalc_Figure_01_02_205.jpg?revision=1&size=bestfit&width=250&height=250)
31)
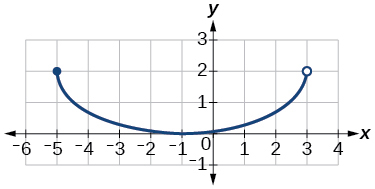
- Answer
-
domain: \(\left[−5, 3\right)\), range: \([0,2]\)
32)
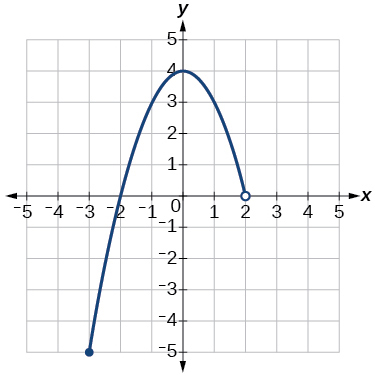
33)
![Graph of a function from (-infinity, 2].](https://math.libretexts.org/@api/deki/files/1098/CNX_Precalc_Figure_01_02_208.jpg?revision=1)
- Answer
-
domain: \(\left(−\infty,1\right]\), range: \(\left[0,\infty\right)\)
34)
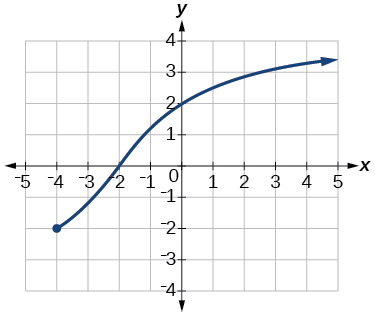
35)
![Graph of a function from [-6, -1/6]U[1/6, 6]/.](https://math.libretexts.org/@api/deki/files/1100/CNX_Precalc_Figure_01_02_210.jpg?revision=1)
- Answer
-
domain: \([−6,−16]\cup[16,6]\); range: \([−6,−16]\cup[16,6]\)
36)
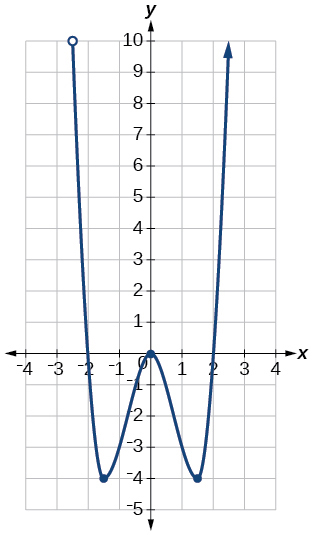
37)
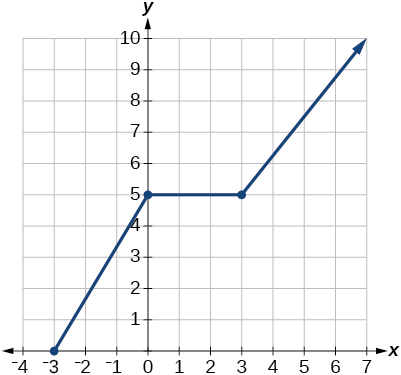
- Answer
-
domain: \(\left[−3, \infty\right)\); range: \(\left[0,\infty\right)\)
For the exercises 38-45, sketch a graph of the piecewise function. Write the domain in interval notation.
38) \(f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}\)
39) \(f(x)= \begin{cases} 2x-1 & \text{if $x < 1$} \\ 1+x & \text{if $x {\geq} 1$} \end{cases}\)
- Answer
-
domain: \((−\infty,\infty)\)
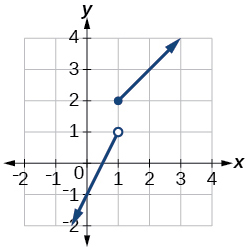
40) \(f(x)= \begin{cases} x+1 & \text{if $x < 0$} \\ x-1 & \text{if $x > 0$} \end{cases}\)
41) \(f(x)= \begin{cases} 3 & \text{if $x < 0$} \\ \sqrt{x} & \text{if $x {\geq} 0$} \end{cases}\)
- Answer
-
domain: \((−\infty,\infty)\)
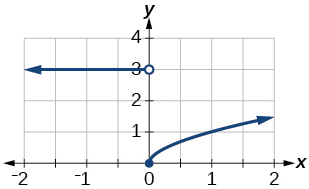
42) \(f(x)= \begin{cases} x^2 & \text{if $x < 0$} \\ 1-x & \text{if $x > 0$} \end{cases}\)
43) \(f(x)= \begin{cases} x^2 & \text{if $x < 0$} \\ x+2 & \text{if $x {\geq} 0$} \end{cases}\)
- Answer
-
domain: \((−\infty,\infty)\)
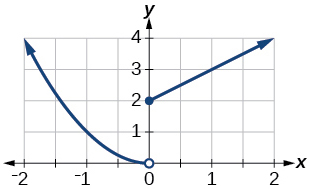
44) \(f(x)= \begin{cases} x+1 & \text{if $x < 1$} \\ x^3 & \text{if $x {\geq} 1$} \end{cases}\)
45) \(f(x)= \begin{cases} |x| & \text{if $x < 2$} \\ 1 & \text{if $x {\geq} 2$} \end{cases}\)
- Answer
-
domain: \((−\infty,\infty)\)
Numeric
For the exercises 46-48, given each function \(f\),evaluate \(f(−3)\), \(f(−2)\), \(f(−1)\), and \(f(0)\).
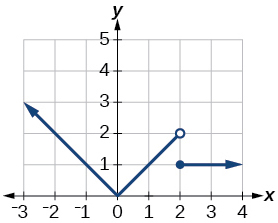
46) \(f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}\)
47) \(f(x)= \begin{cases} 1 & \text{if $x \leq -3$} \\ 0 & \text{if $x > -3$} \end{cases}\)
- Answer
-
\(f(−3)=1\); \(f(−2)=0\); \(f(−1)=0\); \(f(0)=0\)
48) \(f(x)= \begin{cases} -2x^2+3 & \text{if $x \leq -1$} \\ 5x-7 & \text{if $x > -1$} \end{cases}\)
For the exercises 49-51, given each function \(f\), evaluate \(f(−1)\), \(f(0)\), \(f(2)\), and \(f(4)\).
49) \(f(x)= \begin{cases} 7x+3 & \text{if $x < 0$} \\ 7x+6 & \text{if $x {\geq} 0$} \end{cases}\)
- Answer
-
\(f(−1)=−4\); \(f(0)=6\); \(f(2)=20\); \(f(4)=34\)
50) \(f(x)= \begin{cases} x^2-2 & \text{if $x < 2$} \\ 4+|x-5| & \text{if $x {\geq} 2$} \end{cases}\)
51) \(f(x)= \begin{cases} 5x & \text{if $x < 0$} \\ 3 & \text{if $0 {\geq} x {\leq} 2$} \\ x^2 & \text{if $x > 3$} \end{cases}\)
- Answer
-
\(f(−1)=−5\); \(f(0)=3\); \(f(2)=3\); \(f(4)=16\)
For the exercises 52-54, write the domain for the piecewise function in interval notation.
52) \(f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}\)
53) \(f(x)= \begin{cases} x^2-2 & \text{if $x < 1$} \\ -x^2+2 & \text{if $x > 1$} \end{cases}\)
- Answer
-
domain: \((−\infty,1)\cup(1,\infty)\)
54) \(f(x)= \begin{cases} x^2-3 & \text{if $x < 0$} \\ -3x^2 & \text{if $x {\geq} 2$} \end{cases}\)
Technology
55) Graph \(y=\dfrac{1}{x^2}\) on the viewing window \([−0.5,−0.1]\) and \([0.1,0.5]\). Determine the corresponding range for the viewing window. Show the graphs.
- Answer
-
window: \([−0.5,−0.1]\); range: \([4, 100]\)
![Graph of the equation from [-0.5, -0.1].](https://math.libretexts.org/@api/deki/files/1107/CNX_Precalc_Figure_01_02_221.jpg?revision=1)
window: \([0.1, 0.5]\); range: \([4, 100]\)
![Graph of the equation from [0.1, 0.5].](https://math.libretexts.org/@api/deki/files/1108/CNX_Precalc_Figure_01_02_222.jpg?revision=1)
56) Graph \(y=\dfrac{1}{x}\) on the viewing window \([−0.5,−0.1]\) and \([0.1, 0.5]\). Determine the corresponding range for the viewing window. Show the graphs.
Extension
57) Suppose the range of a function \(f\) is \([−5, 8]\). What is the range of \(|f(x)|\)?
- Answer
-
\([0, 8]\)
58) Create a function in which the range is all nonnegative real numbers.
59) Create a function in which the domain is \(x>2\).
- Answer
-
Many answers. One function is \(f(x)=\dfrac{1}{\sqrt{x-2}}\).
Real-World Applications
60) The height \(h\) of a projectile is a function of the time \(t\) it is in the air. The height in feet for \(t\) seconds is given by the function \(h(t)=−16t^2+96t\). What is the domain of the function? What does the domain mean in the context of the problem?
- Answer
-
The domain is \([0, 6]\); it takes 6 seconds for the projectile to leave the ground and return to the ground
61) The cost in dollars of making \(x\) items is given by the function \(C(x)=10x+500\).
a. The fixed cost is determined when zero items are produced. Find the fixed cost for this item.
b. What is the cost of making \(25\) items?
c. Suppose the maximum cost allowed is \(\$1500\). What are the domain and range of the cost function, \(C(x)\)?
1.3: Rates of Change and Behavior of Graphs
In this section, we will investigate changes in functions. For example, a rate of change relates a change in an output quantity to a change in an input quantity. The average rate of change is determined using only the beginning and ending data. Identifying points that mark the interval on a graph can be used to find the average rate of change. Comparing pairs of input and output values in a table can also be used to find the average rate of change.
Verbal
1) Can the average rate of change of a function be constant?
- Answer
-
Yes, the average rate of change of all linear functions is constant.
2) If a function \(f\) is increasing on \((a,b)\) and decreasing on \((b,c)\), then what can be said about the local extremum of \(f\) on \((a,c)\)?
3) How are the absolute maximum and minimum similar to and different from the local extrema?
- Answer
-
The absolute maximum and minimum relate to the entire graph, whereas the local extrema relate only to a specific region around an open interval.
4) How does the graph of the absolute value function compare to the graph of the quadratic function, \(y=x^2\), in terms of increasing and decreasing intervals?
Algebraic
For the exercises 5-15, find the average rate of change of each function on the interval specified for real numbers \(b\) or \(h\).
5) \(f(x)=4x^2−7\) on \([1, b]\)
- Answer
-
\(4(b+1)\)
6) \(g(x)=2x^2−9\) on \([4, b]\)
7) \(p(x)=3x+4\) on \([2, 2+h]\)
- Answer
-
\(3\)
8) \(k(x)=4x−2\) on \([3, 3+h]\)
9) \(f(x)=2x^2+1\) on \([x,x+h]\)
- Answer
-
\(4x+2h\)
10) \(g(x)=3x^2−2\) on \([x,x+h]\)
11) \(a(t)=\dfrac{1}{t+4}\) on \([9,9+h]\)
- Answer
-
\(\dfrac{−1}{13(13+h)}\)
12) \(b(x)=1x+3\) on \([1,1+h]\)
13) \(j(x)=3x^3\) on \([1,1+h]\)
- Answer
-
\(3h^2+9h+9\)
14) \(r(t)=4t^3\) on \([2,2+h]\)
15) \(\dfrac{f(x+h)−f(x)}{h}\) given \(f(x)=2x^2−3x\) on \([x,x+h]\)
- Answer
-
\(4x+2h−3\)
Graphical
For the exercises 16-17, consider the graph of \(f\) shown in the Figure below
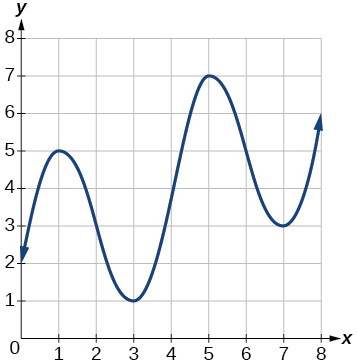
Graph of a polynomial.
16) Estimate the average rate of change from \(x=1\) to \(x=4\).
17) Estimate the average rate of change from \(x=2\) to \(x=5\).
- Answer
-
\(\dfrac{4}{3}\)
For the following exercises, use the graph of each function to estimate the intervals on which the function is increasing or decreasing.
18)

19)
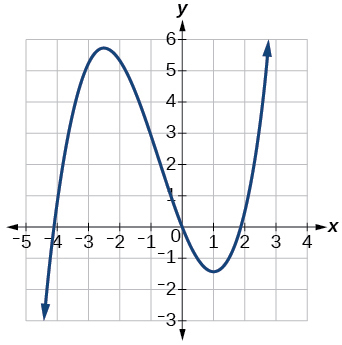
- Answer
-
increasing on \((−\infty,−2.5)\cup(1,\infty)\), decreasing on \((−2.5, 1)\)
20)
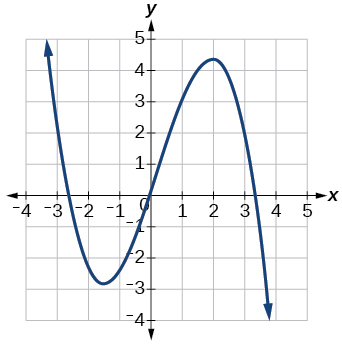
21)
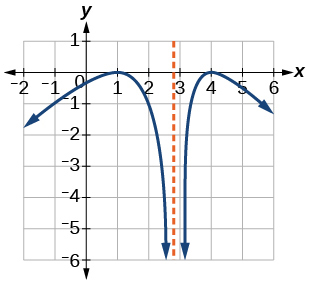
- Answer
-
increasing on \((−\infty,1)\cup(3,4)\), decreasing on \((1,3)\cup(4,\infty)\)
For the exercises 22-23, consider the graph shown in the Figure below.
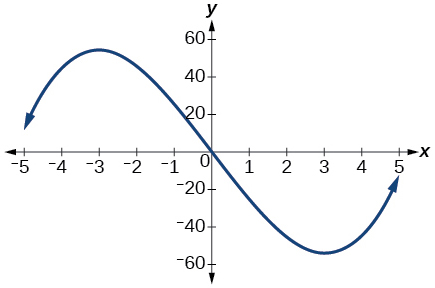
Graph of a cubic function.
22) Estimate the intervals where the function is increasing or decreasing.
23) Estimate the point(s) at which the graph of f has a local maximum or a local minimum.
- Answer
-
local maximum: \((−3, 60)\), local minimum: \((3, −60)\)
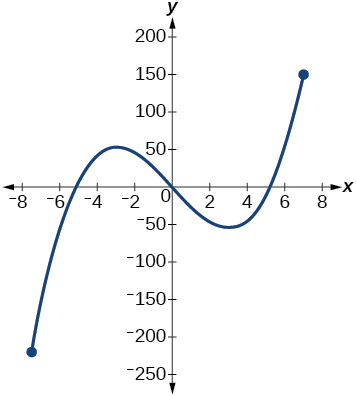
For the exercises 24-25, consider the graph in the Figure below.
Graph of a cubic function.
24) If the complete graph of the function is shown, estimate the intervals where the function is increasing or decreasing.
25) If the complete graph of the function is shown, estimate the absolute maximum and absolute minimum.
- Answer
-
absolute maximum at approximately \((7, 150)\), absolute minimum at approximately \((−7.5, −220)\)
Numeric
26) The Table below gives the annual sales (in millions of dollars) of a product from 1998 to 2006. What was the average rate of change of annual sales (a) between 2001 and 2002, and (b) between 2001 and 2004?
| Year | Sales (millions of dollars) |
|---|---|
| 1998 | 201 |
| 1999 | 219 |
| 2000 | 233 |
| 2001 | 243 |
| 2002 | 249 |
| 2003 | 251 |
| 2004 | 249 |
| 2005 | 243 |
| 2006 | 233 |
27) The Table below gives the population of a town (in thousands) from 2000 to 2008. What was the average rate of change of population (a) between 2002 and 2004, and (b) between 2002 and 2006?
| Year | Population (thousands) |
|---|---|
| 2000 | 87 |
| 2001 | 84 |
| 2002 | 83 |
| 2003 | 80 |
| 2004 | 77 |
| 2005 | 76 |
| 2006 | 78 |
| 2007 | 81 |
| 2008 | 85 |
- Answer
-
a. \(-3000\); b. \(-1250\)
For the exercises 28-34, find the average rate of change of each function on the interval specified.
28) \(f(x)=x^2\) on \([1, 5]\)
29) \(h(x)=5−2x^2\) on \([−2,4]\)
- Answer
-
\(-4\)
30) \(q(x)=x^3\) on \([−4,2]\)
31) \(g(x)=3x^3−1\) on \([−3,3]\)
- Answer
-
\(27\)
32) \(y=\dfrac{1}{x}\) on \([1, 3]\)
33) \(p(t)=\dfrac{(t^2-4)(t+1)}{t^2+3}\) on \([-3,1]\)
- Answer
-
\(-0.167\)
34) \(k(t)=6t^2+\dfrac{4}{t^3}\) on \([−1,3]\)
Technology
For the exercises 35-40, use a graphing utility to estimate the local extrema of each function and to estimate the intervals on which the function is increasing and decreasing.
35) \(f(x)=x^4−4x^3+5\)
- Answer
-
Local minimum at \((3,−22)\), decreasing on \((−\infty, 3)\), increasing on \((3, \infty)\)
36) \(h(x)=x^5+5x^4+10x^3+10x^2−1\)
37) \(g(t)=t\sqrt{t+3}\)
- Answer
-
Local minimum at \((−2,−2)\), decreasing on \((−3,−2)\), increasing on \((−2, \infty)\)
38) \(k(t)=3t^{\frac{2}{3}}−t\)
39) \(m(x)=x^4+2x^3−12x^2−10x+4\)
- Answer
-
Local maximum at \((−0.5, 6)\), local minima at \((−3.25,−47)\) and \((2.1,−32)\), decreasing on \((−\infty,−3.25)\) and \((−0.5, 2.1)\), increasing on \((−3.25, −0.5)\) and \((2.1,\infty)\)
40) \(n(x)=x^4−8x^3+18x^2−6x+2\)
Extension
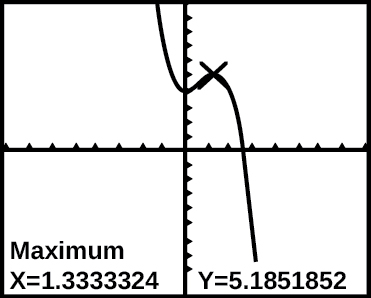
41) The graph of the function \(f\) is shown in the Figure below:
Graph of f(x) on a graphing calculator.
Based on the calculator screen shot, the point \((1.333, 5.185)\) is which of the following?
- a relative (local) maximum of the function
- the vertex of the function
- the absolute maximum of the function
- a zero of the function
- Answer
-
a
42) Let \(f(x)=\dfrac{1}{x}\). Find a number \(c\) such that the average rate of change of the function f on the interval \((1,c)\) is \(-\dfrac{1}{4}\).
43) Let \(f(x)=\dfrac{1}{x}\). Find the number \(b\) such that the average rate of change of f on the interval \((2,b)\) is \(−\dfrac{1}{10}\).
- Answer
-
\(b=5\)
Real-World Applications
44) At the start of a trip, the odometer on a car read \(21,395\). At the end of the trip, \(13.5\) hours later, the odometer read \(22,125\). Assume the scale on the odometer is in miles. What is the average speed the car traveled during this trip?
45) A driver of a car stopped at a gas station to fill up his gas tank. He looked at his watch, and the time read exactly 3:40 p.m. At this time, he started pumping gas into the tank. At exactly 3:44, the tank was full and he noticed that he had pumped \(10.7\) gallons. What is the average rate of flow of the gasoline into the gas tank?
- Answer
-
\(2.7\) gallons per minute
46) Near the surface of the moon, the distance that an object falls is a function of time. It is given by \(d(t)=2.6667t^2\), where \(t\) is in seconds and \(d(t)\) is in feet. If an object is dropped from a certain height, find the average velocity of the object from \(t=1\) to \(t=2\).
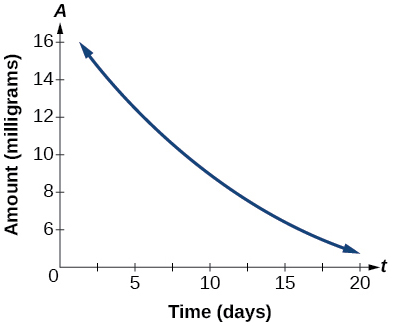
47) The graph in the Figure below illustrates the decay of a radioactive substance over \(t\) days.
Graph of an exponential function.
Use the graph to estimate the average decay rate from \(t=5\) to \(t=15\).
- Answer
-
approximately \(-0.6\) milligrams per day
1.4: Composition of Functions
Suppose we want to calculate how much it costs to heat a house on a particular day of the year. The cost to heat a house will depend on the average daily temperature, and in turn, the average daily temperature depends on the particular day of the year. The cost depends on the temperature, and the temperature depends on the day. By combining these two relationships into one function, we have performed function composition, which is the focus of this section.
Verbal
1) How does one find the domain of the quotient of two functions, \(\dfrac{f}{g}\)?
- Answer
-
Find the numbers that make the function in the denominator \(g\) equal to zero, and check for any other domain restrictions on \(f\) and \(g\), such as an even-indexed root or zeros in the denominator.
2) What is the composition of two functions, \(f{\circ}g\)?
3) If the order is reversed when composing two functions, can the result ever be the same as the answer in the original order of the composition? If yes, give an example. If no, explain why not.
- Answer
-
Yes. Sample answer: Let \(f(x)=x+1\) and \(g(x)=x−1\). Then \(f(g(x))=f(x−1)=(x−1)+1=x\) and \(g(f(x))=g(x+1)=(x+1)−1=x\). So \(f{\circ}g=g{\circ}f\).
4) How do you find the domain for the composition of two functions, \(f{\circ}g\)?
Algebraic
5) Given \(f(x)=x^2+2x\) and \(g(x)=6−x^2\),find \(f+g\), \(f−g\), \(fg\), and \(\dfrac{f}{g}\).Determine the domain for each function in interval notation.
- Answer
-
\((f+g)(x)=2x+6\), domain: \((−\infty,\infty)\)
\((f−g)(x)=2x^2+2x−6\), domain: \((−\infty,\infty)\)
\((fg)(x)=−x^4−2x^3+6x^2+12x\), domain: \((−\infty,\infty)\)
\(\left(\dfrac{f}{g}\right)(x)=\dfrac{x^2+2x}{6−x^2},\) domain: \( (−\infty,−\sqrt{6})\cup(\sqrt{6},\sqrt{6})\cup(\sqrt{6},\infty)\)
6) Given \(f(x)=−3x^2+x\) and \(g(x)=5\), find \(f+g\), \(f−g\), \(fg\), and \(\dfrac{f}{g}\). Determine the domain for each function in interval notation.
7) Given \(f(x)=2x^2+4x\) and \(g(x)=\dfrac{1}{2x}\),find \(f+g\), \(f−g\), \(fg\), and \(\dfrac{f}{g}\). Determine the domain for each function in interval notation.
- Answer
-
\((f+g)(x)=\dfrac{4x^3+8x^2+1}{2x}\), domain: \((−\infty,0)\cup(0,\infty)\)
\((f−g)(x)=\dfrac{4x3+8x2−1}{2x}\), domain: \((−\infty,0)\cup(0,\infty)\)
\((fg)(x)=x+2\), domain: \((−\infty,0)\cup(0,\infty)\)
\((fg)(x)=4x^3+8x^2\), domain: \((−\infty,0)\cup(0,\infty)\)
8) Given \(f(x)=\dfrac{1}{x−4}\) and \(g(x)=\dfrac{1}{6−x}\), find\(f+g\), \(f−g\), \(fg\), and \(\dfrac{f}{g}\). Determine the domain for each function in interval notation.
9) Given \(f(x)=3x^2\) and \(g(x)=\sqrt{x−5}\), find \(f+g\), \(f−g\), \(fg\), and \(\dfrac{f}{g}\). Determine the domain for each function in interval notation.
- Answer
-
\((f+g)(x)=3x^2+\sqrt{x−5}\), domain: \(\left[5,\infty\right)\)
\((f−g)(x)=3x^2−\sqrt{x−5}\), domain: \(\left[5,\infty\right)\)
\((fg)(x)=3x^2\sqrt{x−5}\), domain: \(\left[5,\infty\right)\)
\(\left(\dfrac{f}{g}\right)(x)=\dfrac{3x^2}{\sqrt{x−5}}\), domain: \((5,\infty)\)
10) Given \(f(x)=\sqrt{x}\) and \(g(x)=|x−3|\), find \(\dfrac{g}{f}\). Determine the domain of the function in interval notation.
11) Given \(f(x)=2x^2+1\) and \(g(x)=3x−5\), find the following:
- \(f(g(2))\)
- \(f(g(x))\)
- \(g(f(x))\)
- \((g{\circ}g)(x)\)
- \((f{\circ}f)(−2)\)
- Answer
-
- \(3\)
- \(f(g(x))=2(3x−5)^2+1\)
- \(f(g(x))=6x^2−2\)
- \((g{\circ}g)(x)=3(3x−5)−5=9x−20\)
- \((f{\circ}f)(−2)=163\)
For the exercises 12-17, use each pair of functions to find \(f(g(x))\) and \(g(f(x))\). Simplify your answers.
12) \(f(x)=x^2+1\), \(g(x)=\sqrt{x+2}\)
13) \(f(x)=\sqrt{x}+2\), \(g(x)=x^2+3\)
- Answer
-
\(f(g(x))=\sqrt{x+3}\), \(g(f(x))=x+4\sqrt{x}+7\)
14) \(f(x)=|x|\), \(g(x)=5x+1\)
15) \(f(x)=\sqrt[3]{x}\), \(g(x)=\dfrac{x+1}{x^3}\)
- Answer
-
\(f(g(x))=\sqrt[3]{\dfrac{x+1}{x^3}}=\dfrac{\sqrt[3]{x+1}}{x}\), \(g(f(x))=\dfrac{\sqrt[3]{x}+1}{x}\)
16) \(f(x)=\dfrac{1}{x−6}\), \(g(x)=\dfrac{7}{x}+6\)
17) \(f(x)=\dfrac{1}{x−4}\), \(g(x)=\dfrac{2}{x}+4\)
- Answer
-
\((f{\circ}g)(x)=\dfrac{1}{\frac{2}{x}+4-4}=\dfrac{x}{2}\), \((g{\circ}f)(x)=2x-4\)
For the exercises 18-25, use each set of functions to find f(g(h(x))). Simplify your answers.
18) \(f(x)=x^4+6\), \(g(x)=x−6\), and \(h(x)=\sqrt{x}\)
19) \(f(x)=x^2+1\), \(g(x)=\dfrac{1}{x}\), and \(h(x)=x+3\)
- Answer
-
\(f(g(h(x)))=\left(\dfrac{1}{x+3}\right)^2+1\)
20) Given \(f(x)=\dfrac{1}{x}\) and \(g(x)=x−3\), find the following:
- \((f{\circ}g)(x)\)
- the domain of \((f{\circ}g)(x)\) in interval notation
- \((g{\circ}f)(x)\)
- the domain of \((g{\circ}f)(x)\)
- \(\left(\dfrac{f}{g}\right)x\)
21) Given \(f(x)=\sqrt{2−4x}\) and \(g(x)=−\dfrac{3}{x}\), find the following:
- \((g{\circ}f)(x)\)
- the domain of \((g{\circ}f)(x)\) in interval notation
- Answer
-
- \((g{\circ}f)(x)=−\dfrac{3}{\sqrt{2−4x}}\)
- \(\left(−\infty,\dfrac{1}{2}\right)\)
22) Given the functions \(f(x)=\dfrac{1−x}{x}\) and \(g(x)=\dfrac{1}{1+x^2}\), find the following:
- \((g{\circ}f)(x)\)
- \((g{\circ}f)(2)\)
23) Given functions \(p(x)=\dfrac{1}{\sqrt{x}}\) and \(m(x)=x^2−4\), state the domain of each of the following functions using interval notation:
- \(\dfrac{p(x)}{m(x)}\)
- \(p(m(x))\)
- \(m(p(x))\)
- Answer
-
- \((0,2)\cup(2,\infty)\)
- \((−\infty,−2)\cup(2,\infty)\)
- \((0,\infty)\)
24) Given functions \(q(x)=\dfrac{1}{\sqrt{x}}\) and \(h(x)=x^2−9\), state the domain of each of the following functions using interval notation.
- \(\dfrac{q(x)}{h(x)}\)
- \(q(h(x))\)
- \(h(q(x))\)
25) For \(f(x)=\dfrac{1}{x}\) and \(g(x)=\sqrt{x−1}\), write the domain of \((f{\circ}g)(x)\) in interval notation.
- Answer
-
\((1,\infty)\)
For the exercises 26-41, find functions \(f(x)\) and \(g(x)\) so the given function can be expressed as \(h(x)=f(g(x))\).
26) \(h(x)=(x+2)^2\)
27) \(h(x)=(x−5)^3\)
- Answer
-
sample: \(f(x)=x^3\)
\(g(x)=x−5\)
28) \(h(x)=\dfrac{3}{x−5}\)
29) \(h(x)=\dfrac{4}{(x+2)^2}\)
- Answer
-
sample:\(f(x)=\dfrac{4}{x}\)
\(g(x)=(x+2)^2\)
30) \(h(x)=4+\sqrt[3]{x}\)
31) \(h(x)=\sqrt[3]{\dfrac{1}{2x−3}}\)
- Answer
-
sample:\(f(x)=\sqrt[3]{x}\)
\(g(x)=\dfrac{1}{2x−3}\)
32) \(h(x)=\dfrac{1}{(3x^2−4)^{−3}}\)
33) \(h(x)=\sqrt[4]{\dfrac{3x−2}{x+5}}\)
- Answer
-
sample:\(f(x)=\sqrt[4]{x}\)
\(g(x)=\dfrac{3x−2}{x+5}\)
34) \(h(x)=(\dfrac{8+x^3}{8−x^3})^4\)
35) \(h(x)=\sqrt{2x+6}\)
- Answer
-
sample: \(f(x)=\sqrt{x}\)
\(g(x)=2x+6\)
36) \(h(x)=(5x−1)^3\)
37) \(h(x)=\sqrt[3]{x−1}\)
- Answer
-
sample: \(f(x)=\sqrt[3]{x}\)
\(g(x)=(x−1)\)
38) \(h(x)=|x^2+7|\)
39) \(h(x)=\dfrac{1}{(x−2)^3}\)
- Answer
-
sample: \(f(x)=x^3\)
\(g(x)=\dfrac{1}{x−2}\)
40) \(h(x)=\left(\dfrac{1}{2x−3}\right)^2\)
41) \(h(x)=\sqrt { \dfrac{2x−1}{3x+4}}\)
- Answer
-
sample: \(f(x)=\sqrt{x}\)
\(g(x)=\dfrac{2x−1}{3x+4}\)
Graphical
For the exercises 42-49, use the graphs of \(f\),shown in Figure 1, and \(g\),shown in Figure 2, to evaluate the expressions.
Figure 2: Graph of a function.
42) \(f(g(3))\)
43) \(f(g(1))\)
- Answer
-
\(2\)
44) \(g(f(1))\)
45) \(g(f(0))\)
- Answer
-
\(5\)
46) \(f(f(5))\)
47) \(f(f(4))\)
- Answer
-
\(4\)
48) \(g(g(2))\)
49) \(g(g(0))\)
- Answer
-
\(0\)
For the exercises 50-57, use graphs of \(f(x)\),shown in Figure 3, \(g(x)\),shown in Figure 4, and \(h(x)\),shown in Figure 5, to evaluate the expressions.
Figure 4: Graph of a square root function.
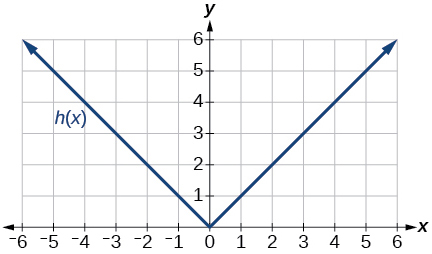
50) \(g(f(1))\)
51) \(g(f(2))\)
- Answer
-
\(2\)
52) \(f(g(4))\)
53) \(f(g(1))\)
- Answer
-
\(1\)
54) \(f(h(2))\)
55) \(h(f(2))\)
- Answer
-
\(4\)
56) \(f(g(h(4)))\)
57) \(f(g(f(−2)))\)
- Answer
-
\(4\)
Numeric
For the exercises 58-65, use the function values for \(f\) and \(g\) shown in the Table below to evaluate each expression.
| \(x\) | \(f(x)\) | \(g(x)\) |
|---|---|---|
| 0 | 7 | 9 |
| 1 | 6 | 5 |
| 2 | 5 | 6 |
| 3 | 8 | 2 |
| 4 | 4 | 1 |
| 5 | 0 | 8 |
| 6 | 2 | 7 |
| 7 | 1 | 3 |
| 8 | 9 | 4 |
| 9 | 3 | 0 |
58) \(f(g(8))\)
59) \(f(g(5))\)
- Answer
-
\(9\)
60) \(g(f(5))\)
61) \(g(f(3))\)
- Answer
-
\(4\)
62) \(f(f(4))\)
63) \(f(f(1))\)
- Answer
-
\(2\)
64) \(g(g(2))\)
65) \(g(g(6))\)
- Answer
-
\(3\)
For the exercises 66-71, use the function values for \(f\) and \(g\) shown in the Table below to evaluate the expressions.
| \(x\) | \(f(x)\) | \(g(x)\) |
|---|---|---|
| -3 | 11 | -8 |
| -2 | 9 | -3 |
| -1 | 7 | 0 |
| 0 | 5 | 1 |
| 1 | 3 | 0 |
| 2 | 1 | -3 |
| 3 | -1 | -8 |
66) \((f{\circ}g)(1)\)
67) \((f{\circ}g)(2)\)
- Answer
-
\(11\)
68) \((g{\circ}f)(2)\)
69) \((g{\circ}f)(3)\)
- Answer
-
\(0\)
70) \((g{\circ}g)(1)\)
71) \((f{\circ}f)(3)\)
- Answer
-
\(7\)
For the exercises 72-75, use each pair of functions to find \(f(g(0))\) and \(g(f(0))\).
72) \(f(x)=4x+8\), \(g(x)=7−x^2\)
73) \(f(x)=5x+7\), \(g(x)=4−2x^2\)
- Answer
-
\(f(g(0))=27\), \(g(f(0))=−94\)
74) \(f(x)=\sqrt{x+4}\), \(g(x)=12−x^3\)
75) \(f(x)=\frac{1}{x+2}\), \(g(x)=4x+3\)
- Answer
-
\(f(g(0))=\frac{1}{5}\), \(g(f(0))=5\)
For the exercises 76-79, use the functions \(f(x)=2x^2+1\) and \(g(x)=3x+5\) to evaluate or find the composite function as indicated.
76) \(f(g(2))\)
77) \(f(g(x))\)
- Answer
-
\(18x^2+60x+51\)
78) \(g(f(−3))\)
79) \((g{\circ}g)(x)\)
- Answer
-
\(g{\circ}g(x)=9x+20\)
Extensions
For the exercises 80-84, use \(f(x)=x^3+1\) and \(g(x)=\sqrt[3]{x−1}\).
80) Find \((f{\circ}g)(x)\) and \((g{\circ}f)(x)\). Compare the two answers.
81) Find \((f{\circ}g)(2)\) and \((g{\circ}f)(2)\).
- Answer
-
\(2\)
82) What is the domain of \((g{\circ}f)(x)\)?
83) What is the domain of \((f{\circ}g)(x)\)?
- Answer
-
\((−\infty,\infty)\)
84) Let \(f(x)=\frac{1}{x}\).
- Find \((f{\circ}f)(x)\).
- Is \((f{\circ}f)(x)\) for any function \(f\) the same result as the answer to part (a) for any function? Explain.
For the exercises 85-87, let \(F(x)=(x+1)^5\), \(f(x)=x^5\), and \(g(x)=x+1\).
85) True or False: \((g{\circ}f)(x)=F(x)\).
- Answer
-
False
86) True or False: \((f{\circ}g)(x)=F(x)\).
For the exercises 87-89, find the composition when \(f(x)=x^2+2\) for all \(x\geq0\) and \(g(x)=\sqrt{x−2}\).
87) \((f{\circ}g)(6)\); \((g{\circ}f)(6)\)
- Answer
-
\((f{\circ}g)(6)=6\); \((g{\circ}f)(6)=6\)
88) \((g{\circ}f)(a)\); \((f{\circ}g)(a)\)
89) \((f{\circ}g)(11)\); \((g{\circ}f)(11)\)
- Answer
-
\((f{\circ}g)(11)=11\), \((g{\circ}f)(11)=11\)
Real-World Applications
90) The function \(D(p)\) gives the number of items that will be demanded when the price is \(p\). The production cost \(C(x)\) is the cost of producing \(x\) items. To determine the cost of production when the price is \(\$6\), you would do which of the following?
- Evaluate \(D(C(6))\)
- Evaluate \(C(D(6))\)
- Solve \(D(C(x))=6\)
- Solve \(C(D(p))=6\)
91) The function \(A(d)\) gives the pain level on a scale of \(0\) to \(10\) experienced by a patient with \(d\) milligrams of a pain-reducing drug in her system. The milligrams of the drug in the patient’s system after \(t\) minutes is modeled by \(m(t)\). Which of the following would you do in order to determine when the patient will be at a pain level of \(4\)?
- Evaluate \(A(m(4))\)
- Evaluate \(m(A(4))\)
- Solve \(A(m(t))=4\)
- Solve \(m(A(d))=4\)
- Answer
-
c
92) A store offers customers a \(30\%\) discount on the price \(x\) of selected items. Then, the store takes off an additional \(15\%\) at the cash register. Write a price function \(P(x)\) that computes the final price of the item in terms of the original price \(x\). (Hint: Use function composition to find your answer.)
93) A rain drop hitting a lake makes a circular ripple. If the radius, in inches, grows as a function of time in minutes according to \(r(t)=25\sqrt{t+2}\), find the area of the ripple as a function of time. Find the area of the ripple at \(t=2\).
- Answer
-
\(A(t)=\pi(25\sqrt{t+2})^2\) and \(A(2)=\pi(25\sqrt{4})^2=2500\pi\) square inches
94) A forest fire leaves behind an area of grass burned in an expanding circular pattern. If the radius of the circle of burning grass is increasing with time according to the formula \(r(t)=2t+1\), express the area burned as a function of time, \(t\) (minutes).
95) Use the function you found in the previous exercise to find the total area burned after \(5\) minutes.
- Answer
-
\(A(5)=\pi(2(5)+1)2=121\pi\) square units
96) The radius \(r\), in inches, of a spherical balloon is related to the volume, \(V\), by \(r(V)=\sqrt[3]{\frac{3V}{4\pi}}\). Air is pumped into the balloon, so the volume after \(t\) seconds is given by \(V(t)=10+20t\).
- Find the composite function \(r(V(t))\).
- Find the exact time when the radius reaches 10 inches.
97) The number of bacteria in a refrigerated food product is given by \(N(T)=23T^2−56T+1\), \(3<T<33\), where \(T\) is the temperature of the food. When the food is removed from the refrigerator, the temperature is given by \(T(t)=5t+1.5\), where \(t\) is the time in hours.
- Find the composite function \(N(T(t))\).
- Find the time (round to two decimal places) when the bacteria count reaches 6752.
- Answer
-
- \(N(T(t))=23(5t+1.5)^2−56(5t+1.5)+1\)
- \(3.38\) hours
1.5: Transformation of Functions
Often when given a problem, we try to model the scenario using mathematics in the form of words, tables, graphs, and equations. One method we can employ is to adapt the basic graphs of the toolkit functions to build new models for a given scenario. There are systematic ways to alter functions to construct appropriate models for the problems we are trying to solve.
Verbal
1) When examining the formula of a function that is the result of multiple transformations, how can you tell a horizontal shift from a vertical shift?
- Answer
-
A horizontal shift results when a constant is added to or subtracted from the input. A vertical shifts results when a constant is added to or subtracted from the output.
2) When examining the formula of a function that is the result of multiple transformations, how can you tell a horizontal stretch from a vertical stretch?
3) When examining the formula of a function that is the result of multiple transformations, how can you tell a horizontal compression from a vertical compression?
- Answer
-
A horizontal compression results when a constant greater than \(1\) is multiplied by the input. A vertical compression results when a constant between \(0\) and \(1\) is multiplied by the output.
4) When examining the formula of a function that is the result of multiple transformations, how can you tell a reflection with respect to the \(x\)-axis from a reflection with respect to the \(y\)-axis?
5) How can you determine whether a function is odd or even from the formula of the function?
- Answer
-
For a function \(f\), substitute (−x) for (x) in \(f(x)\). Simplify. If the resulting function is the same as the original function, \(f(−x)=f(x)\), then the function is even. If the resulting function is the opposite of the original function, \(f(−x)=−f(x)\), then the original function is odd. If the function is not the same or the opposite, then the function is neither odd nor even.
Algebraic
6) Write a formula for the function obtained when the graph of \(f(x)=\sqrt{x}\) is shifted up \(1\) unit and to the left \(2\) units.
7) Write a formula for the function obtained when the graph of \(f(x)=|x|\) is shifted down \(3\) units and to the right \(1\) unit.
- Answer
-
\(g(x)=|x-1|−3\)
8) Write a formula for the function obtained when the graph of \(f(x)=\dfrac{1}{x}\) is shifted down \(4\) units and to the right \(3\) units.
9) Write a formula for the function obtained when the graph of \(f(x)=\dfrac{1}{x^2}\) is shifted up \(2\) units and to the left \(4\) units.
- Answer
-
\(g(x)=\dfrac{1}{(x+4)^2}+2\)
For the exercises 10-19, describe how the graph of the function is a transformation of the graph of the original function \(f\).
10) \(y=f(x−49)\)
11) \(y=f(x+43)\)
- Answer
-
The graph of \(f(x+43)\) is a horizontal shift to the left \(43\) units of the graph of \(f\).
12) \(y=f(x+3)\)
13) \(y=f(x−4)\)
- Answer
-
The graph of \(f(x-4)\) is a horizontal shift to the right \(4\) units of the graph of \(f\).
14) \(y=f(x)+5\)
15) \(y=f(x)+8\)
- Answer
-
The graph of \(f(x)+8\) is a vertical shift up \(8\) units of the graph of \(f\).
16) \(y=f(x)−2\)
17) \(y=f(x)−7\)
- Answer
-
The graph of \(f(x)−7\) is a vertical shift down \(7\) units of the graph of \(f\).
18) \(y=f(x−2)+3\)
19) \(y=f(x+4)−1\)
- Answer
-
The graph of \(f(x+4)−1\) is a horizontal shift to the left \(4\) units and a vertical shift down \(1\) unit of the graph of \(f\).
For the exercises 20-23, determine the interval(s) on which the function is increasing and decreasing.
20) \(f(x)=4(x+1)^2−5\)
21) \(g(x)=5(x+3)^2−2\)
- Answer
-
decreasing on \((−\infty,−3)\) and increasing on \((−3,\infty)\)
22) \(a(x)=\sqrt{−x+4}\)
23) \(k(x)=−3\sqrt{x}−1\)
- Answer
-
decreasing on \((0, \infty)\)
Graphical
For the exercises 24-26, use the graph of \(f(x)=2^x\) shown in the Figure below to sketch a graph of each transformation of \(f(x)\).
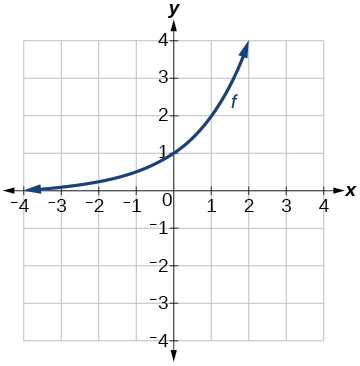
Graph of \(f(x)\).
24) \(h(x)=2^x−3\)
25) \(g(x)=2^x+1\)
- Answer
-
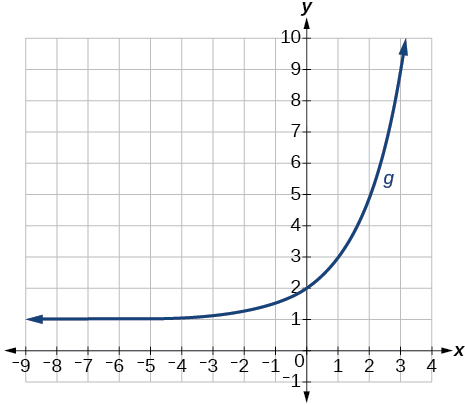
Graph of \(g(x)\)
26) \(w(x)=2^{x−1}\)
For the exercises 27-30, sketch a graph of the function as a transformation of the graph of one of the toolkit functions.
27) \(f(t)=(t+1)^2−3\)
- Answer
-
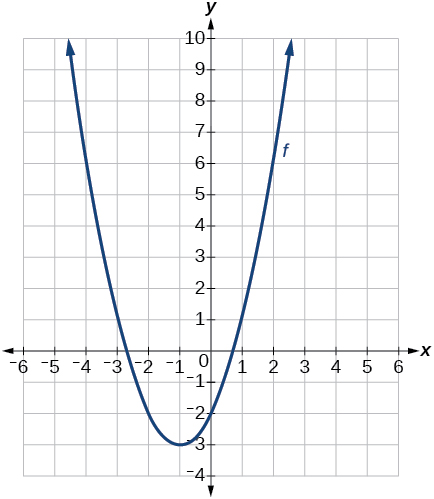
Graph of \(f(t)\).
28) \(h(x)=|x−1|+4\)
29) \(k(x)=(x−2)^3−1\)
- Answer
-
Graph of \(k(x)\).
30) \(m(t)=3+\sqrt{t+2}\)
Numeric
31) Tabular representations for the functions \(f\), \(g\), and \(h\) are given below. Write \(g(x)\) and \(h(x)\) as transformations of \(f(x)\).
| \(x\) | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| \(f(x)\) | -2 | -1 | -3 | 1 | 2 |
| \(x\) | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|
| \(g(x)\) | -2 | -1 | -3 | 1 | 2 |
| \(x\) | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| \(h(x)\) | -1 | 0 | -2 | 2 | 3 |
- Answer
-
\(g(x)=f(x-1)\), \(h(x)=f(x)+1\)
32) Tabular representations for the functions \(f\), \(g\), and \(h\) are given below. Write \(g(x)\) and \(h(x)\) as transformations of \(f(x)\).
| \(x\) | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| \(f(x)\) | -1 | -3 | 4 | 2 | 1 |
| \(x\) | -3 | -2 | -1 | 0 | 1 |
|---|---|---|---|---|---|
| \(g(x)\) | -1 | -3 | 4 | 2 | 1 |
| \(x\) | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| \(h(x)\) | -2 | -4 | 3 | 1 | 0 |
For the exercises 33-40, write an equation for each graphed function by using transformations of the graphs of one of the toolkit functions.
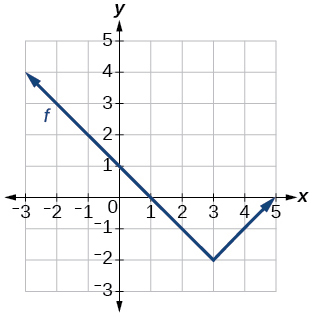
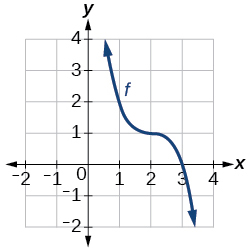
33)
Graph of an absolute function.
- Answer
-
\(f(x)=|x-3|−2\)
34)
Graph of a parabola.
35)
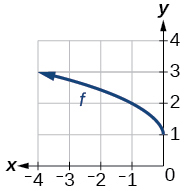
Graph of a square root function.
- Answer
-
\(f(x)=\sqrt{x+3}−1\)
36)
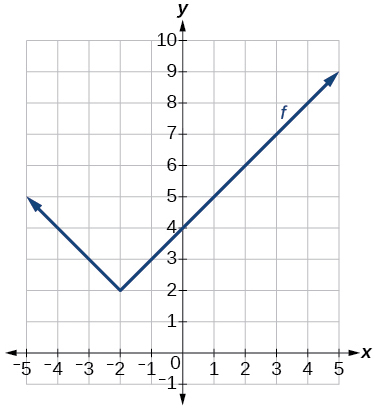
Graph of an absolute function.
37)
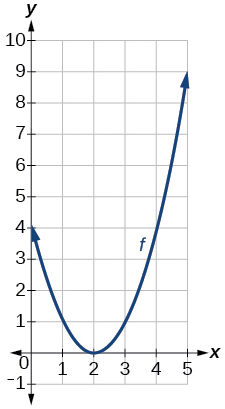
Graph of a parabola
- Answer
-
\(f(x)=(x-2)^2\)
38)
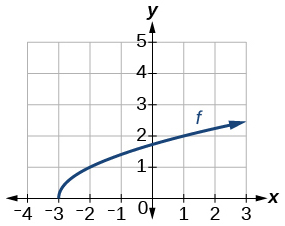
Graph of a square root function.
39)
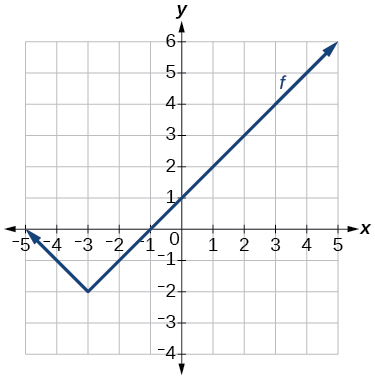
Graph of an absolute function.
- Answer
-
\(f(x)=|x+3|−2\)
40)
Graph of a square root function.
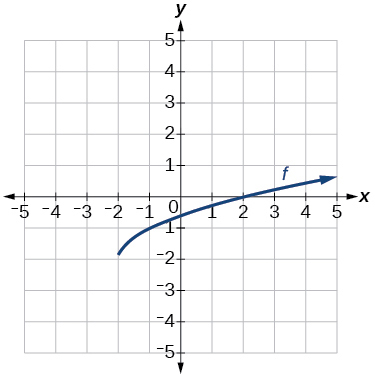
For the exercises 41-42, use the graphs of transformations of the square root function to find a formula for each of the functions.
41)
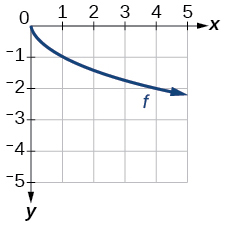
Graph of a square root function.
- Answer
-
\(f(x)=−\sqrt{x}\)
42)
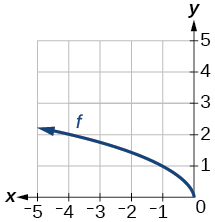
Graph of a square root function.
For the exercises 43-46, use the graphs of the transformed toolkit functions to write a formula for each of the resulting functions.
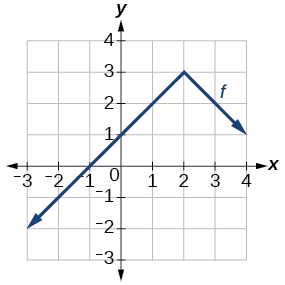
43)
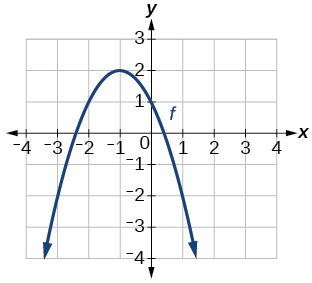
Graph of a parabola.
- Answer
-
\(f(x)=−(x+1)^2+2\)
44)
Graph of a cubic function.
45)
Graph of a square root function.
- Answer
-
\(f(x)=\sqrt{−x}+1\)
46)
Graph of an absolute function.
For the exercises 47-52, determine whether the function is odd, even, or neither.
47) \(f(x)=3x^4\)
- Answer
-
even
48) \(g(x)=\sqrt{x}\)
49) \(h(x)=\dfrac{1}{x}+3x\)
- Answer
-
odd
50) \(f(x)=(x−2)^2\)
51) \(g(x)=2x^4\)
- Answer
-
even
52) \(h(x)=2x−x^3\)
For the exercises 53-62, describe how the graph of each function is a transformation of the graph of the original function \(f\).
53) \(g(x)=−f(x)\)
- Answer
-
The graph of \(g\) is a vertical reflection (across the x-axis) of the graph of \(f\).
54) \(g(x)=f(−x)\)
55) \(g(x)=4f(x)\)
- Answer
-
The graph of \(g\) is a vertical stretch by a factor of 4 of the graph of \(f\).
56) \(g(x)=6f(x)\)
57) \(g(x)=f(5x)\)
- Answer
-
The graph of \(g\) is a horizontal compression by a factor of \(15\) of the graph of \(f\).
58) \(g(x)=f(2x)\)
59) \(g(x)=f \left(\dfrac{1}{3}x \right)\)
- Answer
-
The graph of \(g\) is a horizontal stretch by a factor of 3 of the graph of \(f\).
60) \(g(x)=f \left(\dfrac{1}{5}x \right)\)
61) \(g(x)=3f(−x)\)
- Answer
-
The graph of \(g\) is a horizontal reflection across the y-axis and a vertical stretch by a factor of 3 of the graph of \(f\).
62) \(g(x)=−f(3x)\)
For the exercises 63-68, write a formula for the function \(g\) that results when the graph of a given toolkit function is transformed as described.
63) The graph of \(f(x)=|x|\) is reflected over the \(y\)-axis and horizontally compressed by a factor of \(\dfrac{1}{4}\).
- Answer
-
\(g(x)=|−4x|\)
64) The graph of \(f(x)=\sqrt{x}\) is reflected over the \(x\)-axis and horizontally stretched by a factor of \(2\).
65) The graph of \(f(x)=\dfrac{1}{x^2}\) is vertically compressed by a factor of \(\dfrac{1}{3}\), then shifted to the left \(2\) units and down \(3\) units.
- Answer
-
\(g(x)=\dfrac{1}{3(x+2)^2}−3\)
66) The graph of \(f(x)=\dfrac{1}{x}\) is vertically stretched by a factor of \(8\), then shifted to the right \(4\) units and up \(2\) units.
67) The graph of \(f(x)=x^2\) is vertically compressed by a factor of \(\dfrac{1}{2}\), then shifted to the right \(5\) units and up \(1\) unit.
- Answer
-
\(g(x)=\dfrac{1}{2}(x-5)^2+1\)
68) The graph of \(f(x)=x^2\) is horizontally stretched by a factor of \(3\), then shifted to the left \(4\) units and down \(3\) units.
For the exercises 69-77, describe how the formula is a transformation of a toolkit function. Then sketch a graph of the transformation.
69) \(g(x)=4(x+1)^2−5\)
- Answer
-
The graph of the function \(f(x)=x^2\) is shifted to the left \(1\) unit, stretched vertically by a factor of \(4\), and shifted down \(5\) units.
Graph of a parabola.
70) \(g(x)=5(x+3)^2−2\)
71) \(h(x)=−2|x−4|+3\)
- Answer
-
The graph of \(f(x)=|x|\) is stretched vertically by a factor of \(2\), shifted horizontally \(4\) units to the right, reflected across the horizontal axis, and then shifted vertically \(3\) units up.
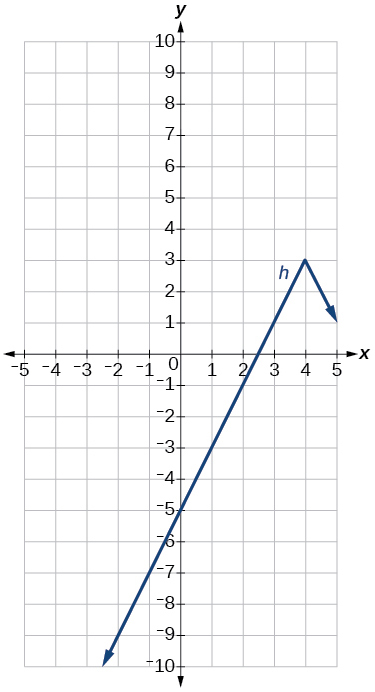
Graph of an absolute value function.
72) \(k(x)=−3\sqrt{x}−1\)
73) \(m(x)=\dfrac{1}{2}x^3\)
- Answer
-
The graph of the function \(f(x)=x^3\) is compressed vertically by a factor of \(\dfrac{1}{2}\).
Graph of a cubic function.
74) \(n(x)=\dfrac{1}{3}|x−2|\)
75) \(p(x)=(\dfrac{1}{3}x)^3−3\)
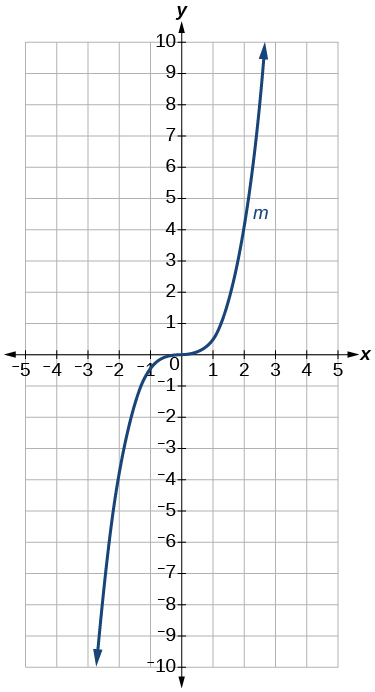
- Answer
-
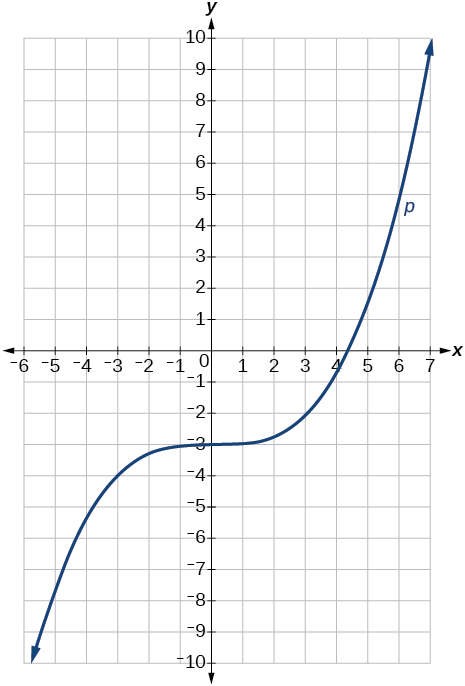
The graph of the function is stretched horizontally by a factor of \(3\) and then shifted vertically downward by \(3\) units.
Graph of a cubic function.
76) \(q(x)=(\dfrac{1}{4}x)^3+1\)
77) \(a(x)=\sqrt{−x+4}\)
- Answer
-
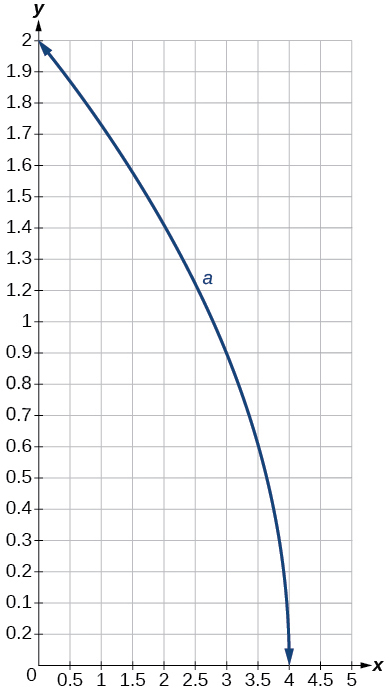
The graph of \(f(x)=\sqrt{x}\) is shifted right \(4\) units and then reflected across the vertical line \(x=4\).
Graph of a square root function.
For the exercises 78-81, use the graph in the Figure below to sketch the given transformations.
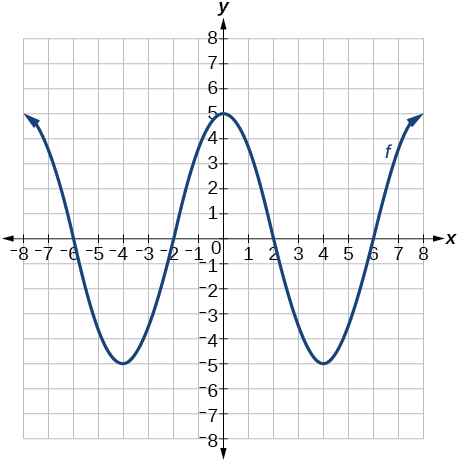
Graph of a polynomial.
78) \(g(x)=f(x)−2\)
79) \(g(x)=−f(x)\)
- Answer
-
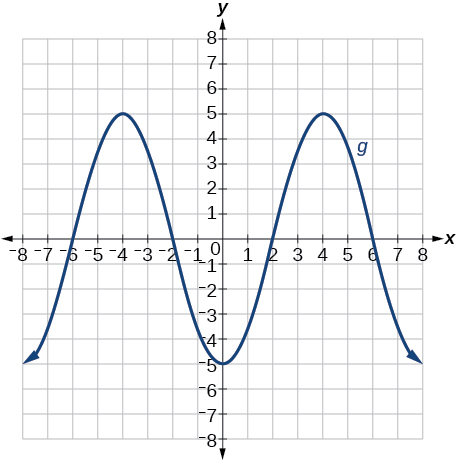
Graph of a polynomial.
80) \(g(x)=f(x+1)\)
81) \(g(x)=f(x−2)\)
- Answer
-
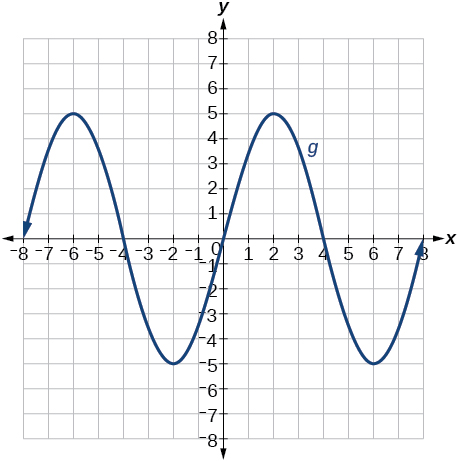
Graph of a polynomial.
1.6: Absolute Value Functions
Distances in the universe can be measured in all directions. As such, it is useful to consider distance as an absolute value function. In this section, we will investigate absolute value functions. The absolute value function is commonly thought of as providing the distance the number is from zero on a number line. Algebraically, for whatever the input value is, the output is the value without regard to sign.
Verbal
1) How do you solve an absolute value equation?
- Answer
-
Isolate the absolute value term so that the equation is of the form \(|A|=B\). Form one equation by setting the expression inside the absolute value symbol, \(A\), equal to the expression on the other side of the equation, \(B\). Form a second equation by setting \(A\) equal to the opposite of the expression on the other side of the equation, \(−B\). Solve each equation for the variable.
2) How can you tell whether an absolute value function has two \(x\)-intercepts without graphing the function?
3) When solving an absolute value function, the isolated absolute value term is equal to a negative number. What does that tell you about the graph of the absolute value function?
- Answer
-
The graph of the absolute value function does not cross the \(x\)-axis, so the graph is either completely above or completely below the \(x\)-axis.
4) How can you use the graph of an absolute value function to determine the \(x\)-values for which the function values are negative?
5) How do you solve an absolute value inequality algebraically?
- Answer
-
First determine the boundary points by finding the solution(s) of the equation. Use the boundary points to form possible solution intervals. Choose a test value in each interval to determine which values satisfy the inequality.
Algebraic
6) Describe all numbers \(x\) that are at a distance of \(4\) from the number \(8\). Express this using absolute value notation.
7) Describe all numbers \(x\) that are at a distance of \(\dfrac{1}{2}\) from the number \(-4\). Express this using absolute value notation.
- Answer
-
\(|x+4|= \dfrac{1}{2}\)
8) Describe the situation in which the distance that point \(x\) is from \(10\) is at least \(15\) units. Express this using absolute value notation.
9) Find all function values \(f(x)\) such that the distance from \(f(x)\) to the value \(8\) is less than \(0.03\) units. Express this using absolute value notation.
- Answer
-
\(|f(x)−8|<0.03\)
For the exercises 10-24, solve the equations below and express the answer using set notation.
10) \(|x+3|=9\)
11) \(|6−x|=5\)
- Answer
-
\({1,11}\)
12) \(|5x−2|=11\)
13) \(|4x−2|=11\)
- Answer
-
\(\left \{\dfrac{9}{4}, \dfrac{13}{4} \right \}\)
14) \(2|4−x|=7\)
15) \(3|5−x|=5\)
- Answer
-
\(\left \{\dfrac{10}{3},\dfrac{20}{3} \right \}\)
16) \(3|x+1|−4=5\)
17) \(5|x−4|−7=2\)
- Answer
-
\(\left \{\dfrac{11}{5}, \dfrac{29}{5} \right \}\)
18) \(0=−|x−3|+2\)
19) \(2|x−3|+1=2\)
- Answer
-
\(\left \{\dfrac{5}{2}, \dfrac{7}{2} \right \}\)
20) \(|3x−2|=7\)
21) \(|3x−2|=−7\)
- Answer
-
No solution
22) \(\left |\dfrac{1}{2}x−5 \right |=11\)
23) \(\left |\dfrac{1}{3}x+5 \right |=14\)
- Answer
-
\(\{−57,27\}\)
24) \(−\left |\dfrac{1}{3}x+5 \right |+14=0\)
For the exercises 25-28, find the \(x\)- and \(y\)-intercepts of the graphs of each function.
25) \(f(x)=2|x+1|−10\)
- Answer
-
\((0,−8)\); \((−6,0)\), \((4,0)\)
26) \(f(x)=4|x−3|+4\)
27) \(f(x)=−3|x−2|−1\)
- Answer
-
\((0,−7)\); no \(x\)-intercepts
28) \(f(x)=−2|x+1|+6\)
For the exercises 29-36, solve each inequality and write the solution in interval notation.
29) \(| x−2 |>10\)
- Answer
-
\((−\infty,−8)\cup(12,\infty)\)
30) \(2|v−7|−4\geq42\)
31) \(|3x−4|\geq8\)
- Answer
-
\(−\dfrac{4}{3}{\leq}x\leq4\)
32) \(|x−4|\geq8\)
33) \(|3x−5|\geq-13\)
- Answer
-
\(\left (−\infty,− \dfrac{8}{3}\right ]\cup\left[6,\infty\right)\)
34) \(|3x−5|\geq−13\)
35) \(|\dfrac{3}{4}x−5|\geq7\)
- Answer
-
\(\left (-\infty,-\dfrac{8}{3}\right ]\cup\left[16,\infty\right)\)
36) \(\left |\dfrac{3}{4}x−5 \right |+1\leq16\)
Graphical
For the exercises 37-39, graph the absolute value function. Plot at least five points by hand for each graph.
37) \(y=|x−1|\)
- Answer
-
38) \(y=|x+1|\)
39) \(y=|x|+1\)
- Answer
-
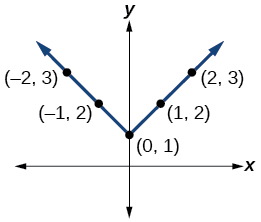
For the exercises 40-52, graph the given functions by hand.
40) \(y=|x|−2\)
41) \(y=−|x|\)
- Answer
-
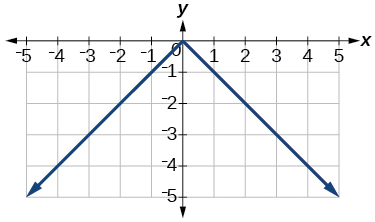
42) \(y=−|x|−2\)
43) \(y=−|x−3|−2\)
- Answer
-
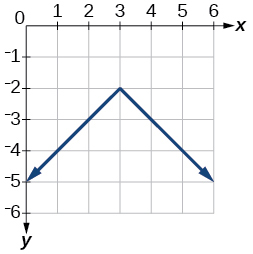
44) \(f(x)=−|x−1|−2\)
45) \(f(x)=−|x+3|+4\)
- Answer
-
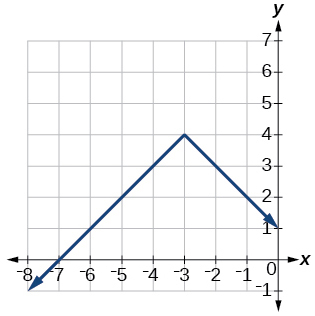
46) \(f(x)=2|x+3|+1\)
47) \(f(x)=3|x−2|+3\)
- Answer
-
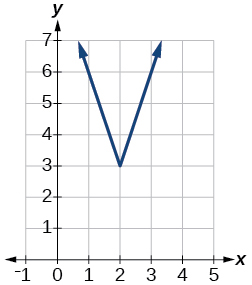
48) \(f(x)=|2x−4|−3\)
49) \(f(x)=|3x+9|+2\)
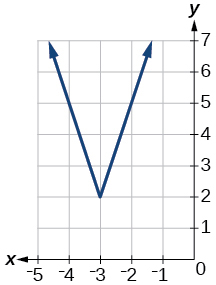
- Answer
-
50) \(f(x)=−|x−1|−3\)
51) \(f(x)=−|x+4|−3\)
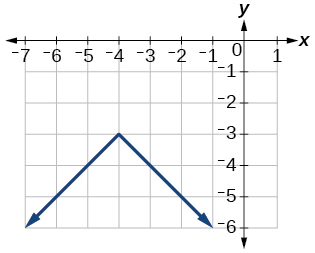
- Answer
-
52) \(f(x)=\dfrac{1}{2}|x+4|−3\)
Technology
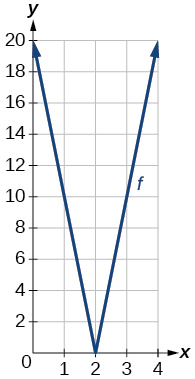
53) Use a graphing utility to graph \(f(x)=10|x−2|\) on the viewing window \([0,4]\). Identify the corresponding range. Show the graph.
- Answer
-
range: \([0,20]\)
54) Use a graphing utility to graph \(f(x)=−100|x|+100\) on the viewing window \([−5,5]\). Identify the corresponding range. Show the graph.
For the exercises 55-56, graph each function using a graphing utility. Specify the viewing window.
55) \(f(x)=−0.1|0.1(0.2−x)|+0.3\)
- Answer
-
\(x\)-intercepts:
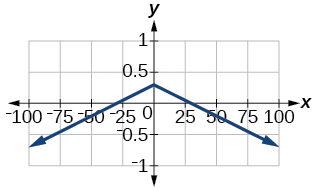
56) \(f(x)=4 \times10^{9}|x−(5 \times 10^9)|+2 \times10^9\)
Extensions
For the exercises 57-59, solve the inequality.
57) \(\left |−2x− \dfrac{2}{3}(x+1) \right |+3>−1\)
- Answer
-
\((−\infty,\infty)\)
58) If possible, find all values of a such that there are no \(x\)-intercepts for \(f(x)=2|x+1|+a\).
59) If possible, find all values of a such that there are no \(y\)-intercepts for \(f(x)=2|x+1|+a\).
- Answer
-
There is no solution for a that will keep the function from having a \(y\)-intercept. The absolute value function always crosses the \(y\)-intercept when \(x=0\).
Real-World Applications
60) Cities A and B are on the same east-west line. Assume that city A is located at the origin. If the distance from city A to city B is at least \(100\) miles and \(x\) represents the distance from city B to city A, express this using absolute value notation.
61) The true proportion \(p\) of people who give a favorable rating to Congress is \(8\%\) with a margin of error of \(1.5\%\). Describe this statement using an absolute value equation.
- Answer
-
\(|p−0.08|\leq0.015\)
62) Students who score within \(18\) points of the number \(82\) will pass a particular test. Write this statement using absolute value notation and use the variable \(x\) for the score.
63) A machinist must produce a bearing that is within \(0.01\) inches of the correct diameter of \(5.0\) inches. Using \(x\) as the diameter of the bearing, write this statement using absolute value notation.
- Answer
-
\(|x−5.0|\leq0.01\)
64) The tolerance for a ball bearing is \(0.01\). If the true diameter of the bearing is to be \(2.0\) inches and the measured value of the diameter is \(x\) inches, express the tolerance using absolute value notation.
1.7: Inverse Functions
If some physical machines can run in two directions, we might ask whether some of the function “machines” we have been studying can also run backwards. In this section, we will consider the reverse nature of functions.
Verbal
1) Describe why the horizontal line test is an effective way to determine whether a function is one-to-one?
- Answer
-
Each output of a function must have exactly one output for the function to be one-to-one. If any horizontal line crosses the graph of a function more than once, that means that \(y\)-values repeat and the function is not one-to-one. If no horizontal line crosses the graph of the function more than once, then no \(y\)-values repeat and the function is one-to-one.
2) Why do we restrict the domain of the function \(f(x)=x^2\) to find the function’s inverse?
3) Can a function be its own inverse? Explain.
- Answer
-
Yes. For example, \(f(x)=\dfrac{1}{x}\) is its own inverse.
4) Are one-to-one functions either always increasing or always decreasing? Why or why not?
5) How do you find the inverse of a function algebraically?
- Answer
-
Given a function \(y=f(x)\), solve for \(x\) in terms of \(y\). Interchange the \(x\) and \(y\). Solve the new equation for \(y\). The expression for \(y\) is the inverse, \(y=f^{-1}(x)\).
Algebraic
6) Show that the function \(f(x)=a−x\) is its own inverse for all real numbers \(a\).
For the exercises 7-12, find \(f^{-1}(x)\) for each function.
7) \(f(x)=x+3\)
- Answer
-
\(f^{-1}(x)=x−3\)
8) \(f(x)=x+5\)
9) \(f(x)=2−x\)
- Answer
-
\(f^{-1}(x)=2−x\)
10) \(f(x)=3−x\)
11) \(f(x)=\dfrac{x}{x+2}\)
- Answer
-
\(f^{-1}(x)=\dfrac{−2x}{x−1}\)
12) \(f(x)=\dfrac{2x+3}{5x+4}\)
For the exercises 13-16, find a domain on which each function \(f\) is one-to-one and non-decreasing. Write the domain in interval notation. Then find the inverse of \(f\) restricted to that domain.
13) \(f(x)=(x+7)^2\)
- Answer
-
domain of \(f(x)\): \(\left[−7,\infty\right)\); \(f^{-1}(x)=\sqrt{x}−7\)
14) \(f(x)=(x−6)^2\)
15) \(f(x)=x^2−5\)
- Answer
-
domain of \(f(x)\): \(\left[0,\infty\right)\); \(f^{-1}(x)=\sqrt{x+5}\)
16) Given \(f(x)=\dfrac{x}{2+x}\) and \(g(x)=\dfrac{2x}{1-x}:\)
- Find \(f(g(x))\) and \(g(f(x))\).
- What does the answer tell us about the relationship between \(f(x)\) and \(g(x)?\)
- Answer
-
a. \(f(g(x))=x\) and \(g(f(x))=x\)
b. This tells us that \(f\) and \(g\) are inverse functions
For the exercises 17-18, use function composition to verify that \(f(x)\) and \(g(x)\) are inverse functions.
17) \(f(x)=\sqrt[3]{x-1}\) and \(g(x)=x^3+1\)
- Answer
-
\(f(g(x))=x\), \(g(f(x))=x\)
18) \(f(x)=−3x+5\) and \(g(x)=\dfrac{x-5}{-3}\)
Graphical
For the exercises 19-22, use a graphing utility to determine whether each function is one-to-one.
19) \(f(x)=\sqrt{x}\)
- Answer
-
one-to-one
20) \(f(x)=\sqrt[3]{3x+1}\)
21) \(f(x)=−5x+1\)
- Answer
-
one-to-one
22) \(f(x)=x^3−27\)
For the exercises 23-24, determine whether the graph represents a one-to-one function.
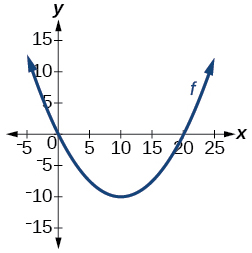
23)
- Answer
-
not one-to-one
24)
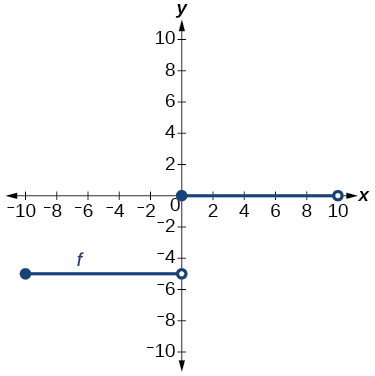
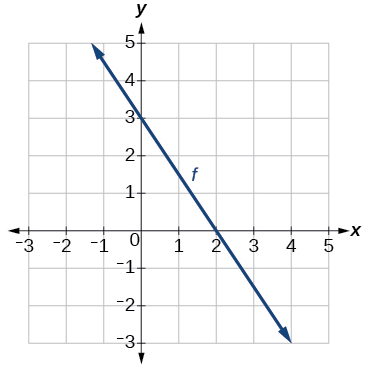
Graph of a line
25) Find \(f(0)\).
- Answer
-
\(3\)
26) Solve \(f(x)=0\).
27) Find \(f^{-1}(0)\).
- Answer
-
\(2\)
28) Solve \(f^{-1}(x)=0\).
For the exercises 29-32, use the graph of the one-to-one function shown in the Figure below
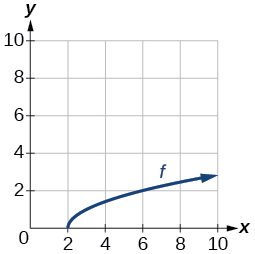
Graph of a square root function.
29) Sketch the graph of \(f^{-1}\).
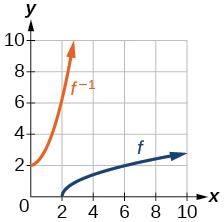
- Answer
-
30) Find \(f(6)\) and \(f^{-1}(2)\).
31) If the complete graph of \(f\) is shown, find the domain of \(f\).
- Answer
-
\([2,10]\)
32) If the complete graph of \(f\) is shown, find the range of \(f\)
Numeric
For the exercises 33-36, evaluate or solve, assuming that the function \(f\) is one-to-one.
33) If \(f(6)=7\), find \(f^{-1}(7)\).
- Answer
-
\(6\)
34) If \(f(3)=2\), find \(f^{-1}(2)\).
35) If \(f^{-1}(−4)=−8\), find \(f(−8)\).
- Answer
-
\(-4\)
36) If \(f^{-1}(−2)\)=−1, find \(f(−1)\).
For the exercises 37-40, use the values listed in the Table below to evaluate or solve.
| \(x\) | \(f(x)\) |
|---|---|
| 0 | 8 |
| 1 | 0 |
| 2 | 7 |
| 3 | 4 |
| 4 | 2 |
| 5 | 6 |
| 6 | 5 |
| 7 | 3 |
| 8 | 9 |
| 9 | 1 |
37) Find \(f(1)\).
- Answer
-
\(0\)
38) Solve \(f(x)=3\).
39) Find \(f^{-1}(0)\).
- Answer
-
\(1\)
40) Solve \(f^{-1}(x)=7\).
41) Use the tabular representation of \(f\) in the Table below to create a table for \(f^{-1}(x)\).
| \(x\) | 3 | 6 | 9 | 13 | 14 |
|---|---|---|---|---|---|
| \(f(x)\) | 1 | 4 | 7 | 12 | 16 |
- Answer
-
\(x\) 1 4 7 12 16 \(f^{-1}(x)\) 3 6 9 13 14
Technology
For the exercises 42-44, find the inverse function. Then, graph the function and its inverse.
42) \(f(x)=\dfrac{3}{x-2}\)
43) \(f(x)=x^3−1\)
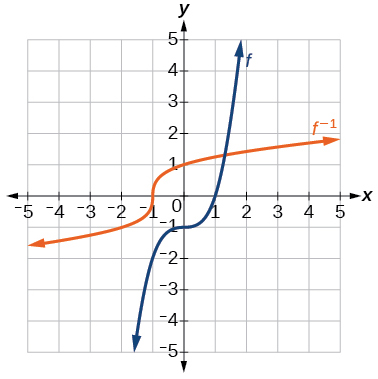
- Answer
-
\(f^{-1}(x)=(1+x)^{1/3}\)
44) Find the inverse function of \(f(x)=\dfrac{1}{x-1}\). Use a graphing utility to find its domain and range. Write the domain and range in interval notation.
Real-World Applications
45) To convert from \(x\) degrees Celsius to \(y\) degrees Fahrenheit, we use the formula \(f(x)=\dfrac{9}{5}x+32\). Find the inverse function, if it exists, and explain its meaning.
- Answer
-
\(f^{-1}(x)=\dfrac{5}{9}(x−32)\). Given the Fahrenheit temperature, \(x\), this formula allows you to calculate the Celsius temperature.
46) The circumference \(C\) of a circle is a function of its radius given by \(C(r)=2{\pi}r\). Express the radius of a circle as a function of its circumference. Call this function \(r(C)\). Find \(r(36\pi)\) and interpret its meaning.
47) A car travels at a constant speed of \(50\) miles per hour. The distance the car travels in miles is a function of time, \(t\), in hours given by \(d(t)=50t\). Find the inverse function by expressing the time of travel in terms of the distance traveled. Call this function \(t(d)\). Find \(t(180)\) and interpret its meaning.
- Answer
-
\(t(d)=\dfrac{d}{50}\), \(t(180)=\dfrac{180}{50}\). The time for the car to travel \(180\) miles is \(3.6\) hours.


