2.R: Linear Functions(Review)
- Page ID
- 19661
2.1 Linear Functions
1) Determine whether the algebraic equation is linear: \(2 x+3 y=7\)
- Answer
-
Yes
2) Determine whether the algebraic equation is linear: \(6 x^{2}-y=5\)
3) Determine whether the function is increasing or decreasing: \(f(x)=7 x-2\)
- Answer
-
Increasing
4) Determine whether the function is increasing or decreasing: \(g(x)=-x+2\)
5) Given each set of information, find a linear equation that satisfies the given conditions, if possible. Passes through \((7,5)\) and \((3,17)\)
- Answer
-
\(y=-3 x+26\)
6) Given each set of information, find a linear equation that satisfies the given conditions, if possible. \(x\) -intercept at \((6,0)\) and \(y\) -intercept at \((0,10)\)
7) Find the slope of the line shown in the line graph.
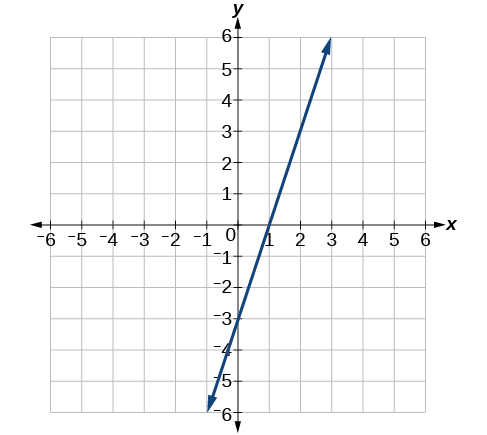
- Answer
-
\(3\)
8) Find the slope of the line graphed.
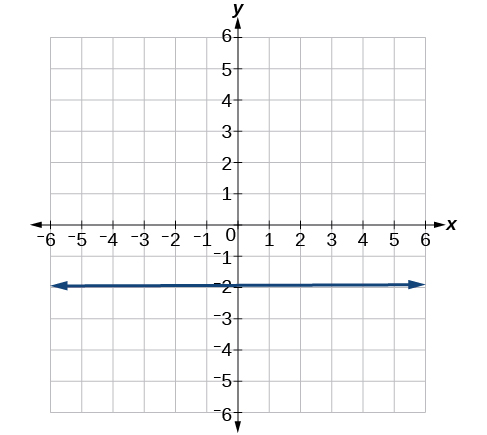
9) Write an equation in slope-intercept form for the line shown.
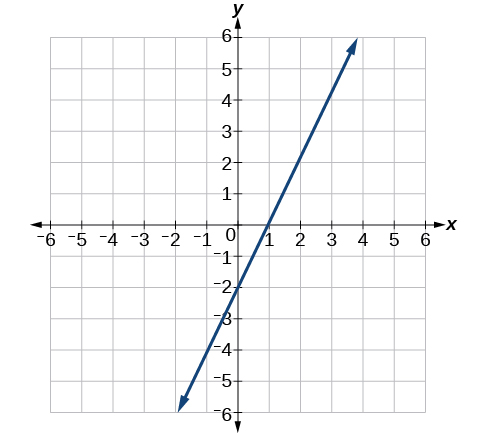
- Answer
-
\(y=2 x-2\)
10) Does the following table represent a linear function? If so, find the linear equation that models the data.
| \(x\) | –4 | 0 | 2 | 10 |
|---|---|---|---|---|
| \(g(x)\) | 18 | –2 | –12 | –52 |
11) Does the following table represent a linear function? If so, find the linear equation that models the data.
| \(x\) | 6 | 8 | 12 | 26 |
|---|---|---|---|---|
| \(g(x)\) | –8 | –12 | –18 | –46 |
- Answer
-
Not linear
12) On June 1st, a company has \(\$4,000,000\) profit. If the company then loses \(150,000\) dollars per day thereafter in the month of June, what is the company’s profit nth day after June 1st?
2.2 Graphs of Linear Functions
For the exercises 1-2, determine whether the lines given by the equations below are parallel, perpendicular, or neither parallel nor perpendicular:
1) \(\begin{align*} 2x-6y &=12 \\ -x+3y &=1 \end{align*} \nonumber\)
- Answer
-
parallel
2) \(\begin{align*} y &=\dfrac{1}{3} x-2 \\ 3x+y &=-9 \end{align*} \nonumber \)
For the exercises 3-4, find the \(x\)- and \(y\)- intercepts of the given equation
3) \(7 x+9 y=-63\)
- Answer
-
\((-9,0); (0,-7)\)
4) \(f(x)=2 x-1\)
For the exercises 5-11, use the descriptions of the pairs of lines to find the slopes of Line 1 and Line 2. Is each pair of lines parallel, perpendicular, or neither?
5)
Line 1: Passes through \((5,11)\) and \((10,1)\)
Line \(2 :\) Passes through \((-1,3)\) and \((-5,11)\)
- Answer
-
Line 1 : \(m=-2\); Line 2 : \(m=-2\); Parallel
6)
Line 1: Passes through \((8,-10)\) and \((0,-26)\)
Line 2: Passes through \((2,5)\) and \((4,4)\)
7) Write an equation for a line perpendicular to \(f(x)=5 x-1\) and passing through the point \((5,20)\).
- Answer
-
\(y=-0.2 x+21\)
8) Find the equation of a line with a \(y\) -intercept of \((0,2)\) and slope \(-\dfrac{1}{2}\).
9) Sketch a graph of the linear function \(f(t)=2t-5\).
- Answer
-
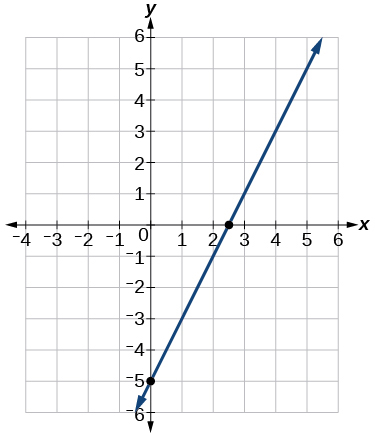
10) Find the point of intersection for the \(2\) linear functions: \(\begin{align*} x &=y+6 \\ 2x-y &=13 \end{align*}\)
11) A car rental company offers two plans for renting a car.
Plan A: \(25\) dollars per day and \(10\) cents per mile
Plan B: \(50\) dollars per day with free unlimited mileage
How many miles would you need to drive for plan B to save you money?
- Answer
-
\(250\)
2.3 Modeling with Linear Functions
1) Find the area of a triangle bounded by the \(y\) axis, the line \(f(x)=10-2x\), and the line perpendicular to \(f\) that passes through the origin.
2) A town’s population increases at a constant rate. In 2010 the population was \(55,000\). By 2012 the population had increased to \(76,000\). If this trend continues, predict the population in 2016.
- Answer
-
\(118,000\)
3) The number of people afflicted with the common cold in the winter months dropped steadily by \(50\) each year since 2004 until 2010. In 2004, \(875\) people were inflicted.
4) Find the linear function that models the number of people afflicted with the common cold \(C\) as a function of the year, \(t\). When will no one be afflicted?
For the exercises 5-6, use the graph in the Figure below showing the profit, \(y\), in thousands of dollars, of a company in a given year, \(x\), where \(x\) represents years since 1980.
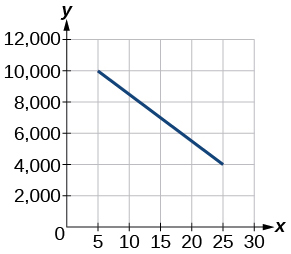
5) Find the linear function \(y\), where \(y\) depends on \(x\), the number of years since 1980.
- Answer
-
\(y=-300 x+11,500\)
6) Find and interpret the \(y\)-intercept.
7) For the following exercise, consider this scenario: In 2004, a school population was \(1,700\). By 2012 the population had grown to \(2,500\). Assume the population is changing linearly.
- How much did the population grow between the year 2004 and 2012?
- What is the average population growth per year?
- Find an equation for the population, \(P\), of the school \(t\) years after 2004.
- Answer
-
- \(800\)
- \(100\) students per year
- \(P(t)=100 t+1700\)
For the exercises 8-9, consider this scenario: In 2000, the moose population in a park was measured to be \(6,500\). By 2010, the population was measured to be \(12,500\). Assume the population continues to change linearly.
8) Find a formula for the moose population, \(P\).
9) What does your model predict the moose population to be in 2020?
- Answer
-
\(18,500\)
For the exercises 10-, consider this scenario: The median home values in subdivisions Pima Central and East Valley (adjusted for inflation) are shown in the Table below. Assume that the house values are changing linearly.
| Year | Pima Central | East Valley |
|---|---|---|
| 1970 | 32,000 | 120,250 |
| 2010 | 85,000 | 150,000 |
10) In which subdivision have home values increased at a higher rate?
11) If these trends were to continue, what would be the median home value in Pima Central in 2015?
- Answer
-
\(\$91,625\)
2.4 Fitting Linear Models to Data
1) Draw a scatter plot for the data in the Table below. Then determine whether the data appears to be linearly related.
| 0 | 2 | 4 | 6 | 8 | 10 |
| –105 | –50 | 1 | 55 | 105 | 160 |
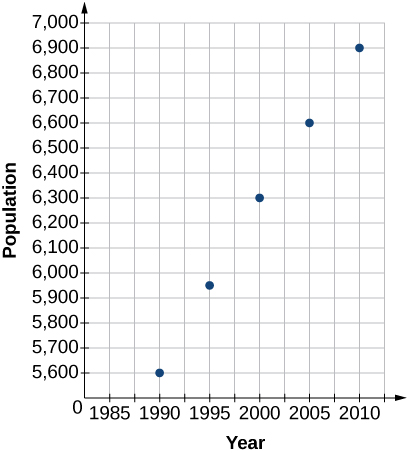
2) Draw a scatter plot for the data in the Table. If we wanted to know when the population would reach \(15,000\), would the answer involve interpolation or extrapolation?
| Year | Population |
|---|---|
| 1990 | 5,600 |
| 1995 | 5,950 |
| 2000 | 6,300 |
| 2005 | 6,600 |
| 2010 | 6,900 |
- Answer
-
Extrapolation
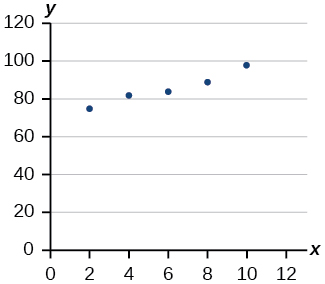
3) Eight students were asked to estimate their score on a \(10\)-point quiz. Their estimated and actual scores are given in the Table. Plot the points, then sketch a line that fits the data.
| Predicted | Actual |
|---|---|
| 6 | 6 |
| 7 | 7 |
| 7 | 8 |
| 8 | 8 |
| 7 | 9 |
| 9 | 10 |
| 10 | 10 |
| 10 | 9 |
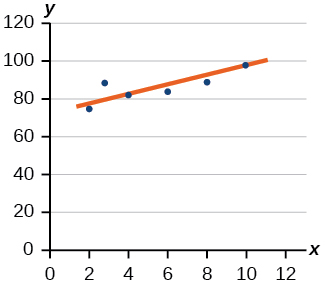
4) Draw a best-fit line for the plotted data.
- Answer
-
For the exercises 5-6, consider the data in the Table below, which shows the percent of unemployed in a city of people \(25\) years or older who are college graduates is given below, by year.
| Year | Percent Graduates |
|---|---|
| 2000 | 6.5 |
| 2002 | 7.0 |
| 2005 | 7.4 |
| 2007 | 8.2 |
| 2010 | 9.0 |
5) Determine whether the trend appears to be linear. If so, and assuming the trend continues, find a linear regression model to predict the percent of unemployed in a given year to three decimal places.
6) In what year will the percentage exceed \(12\%\)?
- Answer
-
Midway through 2024
7) Based on the set of data given in the Table, calculate the regression line using a calculator or other technology tool, and determine the correlation coefficient to three decimal places.
| \(x\) | 17 | 20 | 23 | 26 | 29 |
|---|---|---|---|---|---|
| \(y\) | 15 | 25 | 31 | 37 | 40 |
8) Based on the set of data given in the Table, calculate the regression line using a calculator or other technology tool, and determine the correlation coefficient to three decimal places.
| \(x\) | 10 | 12 | 15 | 18 | 20 |
|---|---|---|---|---|---|
| \(y\) | 36 | 34 | 30 | 28 | 22 |
- Answer
-
\(y=-1.294 x+49.412; r=-0.974\)
For the exercises 9-12, consider this scenario: The population of a city increased steadily over a ten-year span. The following ordered pairs show the population and the year over the ten-year span (population, year) for specific recorded years: \((3,600,2000) ;(4,000,2001) ;(4,700,2003) ;(6,000,2006)\)
9) Use linear regression to determine a function \(y\), where the year depends on the population, to three decimal places of accuracy.
10) Predict when the population will hit \(12,000\).
- Answer
-
Early in 2022
11) What is the correlation coefficient for this model to three decimal places of accuracy?
12) According to the model, what is the population in 2014?
- Answer
-
\(7,660\)
Practice Test
1) Determine whether the following algebraic equation can be written as a linear function: \(2 x+3 y=7\)
- Answer
-
Yes
2) Determine whether the following function is increasing or decreasing: \(f(x)=-2 x+5\)
3) Determine whether the following function is increasing or decreasing: \(f(x)=7 x+9\)
- Answer
-
Increasing
4) Given the following set of information, find a linear equation satisfying the conditions, if possible. Passes through \((5,1)\) and \((3,-9)\)
5) Given the following set of information, find a linear equation satisfying the conditions, if possible. \(x\) intercept at \((-4,0)\) and \(y\) -intercept at \((0,-6)\)
- Answer
-
\(y=-1.5 x-6\)
6) Find the slope of the line in the Figure below.
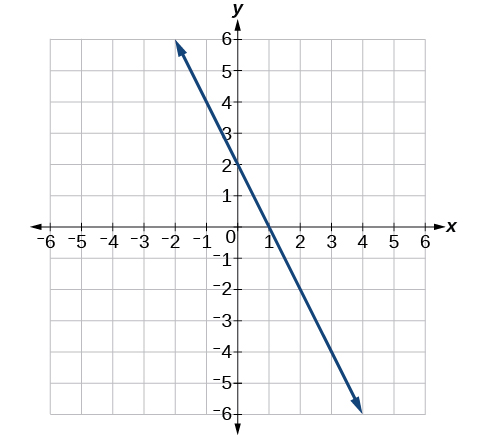
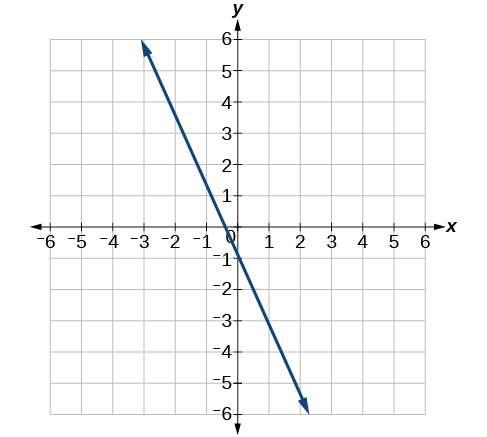
- Answer
-
\(y=-2 x-1\)
8) Does the Table represent a linear function? If so, find a linear equation that models the data.
| \(x\) | –6 | 0 | 2 | 4 |
| \(g(x)\) | 14 | 32 | 38 | 44 |
9) Does the Table represent a linear function? If so, find a linear equation that models the data.
| \(x\) | 1 | 3 | 7 | 11 |
| \(g(x)\) | 4 | 9 | 19 | 12 |
- Answer
-
No
10) At 6 AM, an online company has sold \(120\) items that day. If the company sells an average of \(30\) items per hour for the remainder of the day, write an expression to represent the number of items that were sold \(n\) after 6 AM.
For the exercises 11-22, determine whether the lines given by the equations below are parallel, perpendicular, or neither parallel nor perpendicular:
11) \(\begin{align*}{y=\dfrac{3}{4} x-9} \\ {-4 x-3 y=8}\end{align*}\)
- Answer
-
Perpendicular
12) \(\begin{align*}{-2 x+y=3} \\ {3 x+\dfrac{3}{2} y=5}\end{align*}\)
13) Find the \(x\) - and \(y\) -intercepts of the equation \(2 x+7 y=-14\).
- Answer
-
\((-7,0) ;(0,-2)\)
14) Given below are descriptions of two lines. Find the slopes of Line 1 and Line 2. Is the pair of lines parallel, perpendicular, or neither?
Line \(1 :\) Passes through \((-2,-6)\) and \((3,14)\)
Line \(2 :\) Passes through \((2,6)\) and \((4,14)\)
15) Write an equation for a line perpendicular to \(f(x)=4 x+3\) and passing through the point \((8,10)\).
- Answer
-
\(y=-0.25 x+12\)
16) Sketch a line with a \(y\)-intercept of \((0,5)\) and slope \(-\dfrac{5}{2}\).
17) Graph of the linear function \(f(x)=-x+6\).
- Answer
-
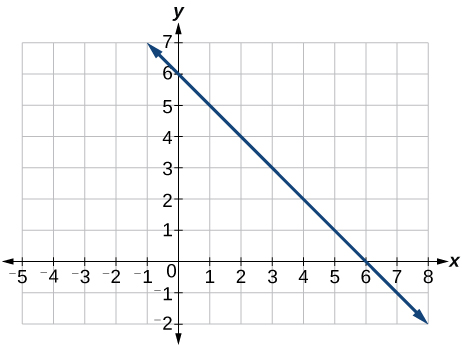
18) For the two linear functions, find the point of intersection: \(\begin{align*} x &=y+2 \\ 2x-3y &=-1 \end{align*}\)
19) A car rental company offers two plans for renting a car.
Plan A: \(\$ 25\) per day and \(\$ 0.10\) per mile
Plan B: \(\$ 40\) per day with free unlimited mileage
How many miles would you need to drive for plan B to save you money?
- Answer
-
\(150\)
20) Find the area of a triangle bounded by the \(y\) axis, the line \(f(x)=12-4 x,\) and the line perpendicular to \(f\) that passes through the origin.
21) A town’s population increases at a constant rate. In 2010 the population was \(65,000\). By 2012 the population had increased to \(90,000\). Assuming this trend continues, predict the population in 2018.
- Answer
-
\(165,000\)
22) The number of people afflicted with the common cold in the winter months dropped steadily by \(25\) each year since 2002 until 2012. In 2002, \(8,040\) people were inflicted. Find the linear function that models the number of people afflicted with the common cold \(C\) as a function of the year, \(t\). When will less than \(6,000\) people be afflicted?
For the exercises 23-24, use the graph in Figure, showing the profit, \(y\), in thousands of dollars, of a company in a given year, \(x\), where \(x\) represents years since 1980.
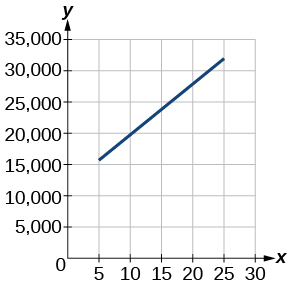
23) Find the linear function \(y\), where \(y\) depends on \(x\), the number of years since 1980.
- Answer
-
\(y=875 x+10,675\)
24) Find and interpret the \(y\)-intercept.
25) In 2004, a school population was \(1250\). By 2012 the population had dropped to \(875\). Assume the population is changing linearly.
- How much did the population drop between the year 2004 and 2012?
- What is the average population decline per year?
- Find an equation for the population, \(P\), of the school \(t\) years after 2004.
- Answer
-
- \(375\)
- dropped an average of \(46.875,\) or about \(47\) people per year
- \(y=-46.875 t+1250\)
26) Draw a scatter plot for the data provided in the Table. Then determine whether the data appears to be linearly related.
| 0 | 2 | 4 | 6 | 8 | 10 |
| –450 | –200 | 10 | 265 | 500 | 755 |
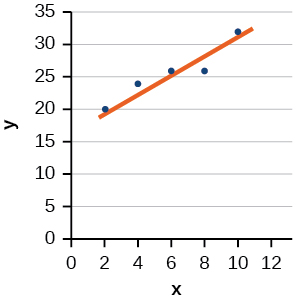
27) Draw a best-fit line for the plotted data.
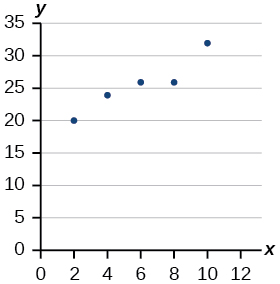
- Answer
-
For the exercises 28-29, use the Table below, which shows the percent of unemployed persons \(25\) years or older who are college graduates in a particular city, by year.
| Year | Percent Graduates |
|---|---|
| 2000 | 8.5 |
| 2002 | 8.0 |
| 2005 | 7.2 |
| 2007 | 6.7 |
| 2010 | 6.4 |
28) Determine whether the trend appears linear. If so, and assuming the trend continues, find a linear regression model to predict the percent of unemployed in a given year to three decimal places.
29) In what year will the percentage drop below \(4\%\)?
- Answer
-
Early in 2018
30) Based on the set of data given in the Table below, calculate the regression line using a calculator or other technology tool, and determine the correlation coefficient. Round to three decimal places of accuracy.
| \(x\) | 16 | 18 | 20 | 24 | 26 |
|---|---|---|---|---|---|
| \(y\) | 106 | 110 | 115 | 120 | 125 |
For the exercises 31-33, consider this scenario: The population of a city increased steadily over a ten-year span. The following ordered pairs shows the population (in hundreds) and the year over the ten-year span, (population, year) for specific recorded years: \((4,500,2000) ;(4,700,2001) ;(5,200,2003) ;(5,800,2006)\)
31) Use linear regression to determine a function y, where the year depends on the population. Round to three decimal places of accuracy.
- Answer
-
\(y=0.00455 x+1979.5\)
32) Predict when the population will hit \(20,000\).
33) What is the correlation coefficient for this model?
- Answer
-
\(r=0.999\)


